新型单相超材料的低频带隙和振动特性研究
摘 要:低频振动和噪声的抑制一直是工程中的重要问题。本文提出了一种新型的单相超材料结构,有望应用于噪声控制。基于布洛赫(Bloch)定理和有限元方法(FEM),数值分析了这种新型结构的带隙特性和带隙形成机制,参数化分析了带隙与几何尺寸的依赖关系,用三维色散曲面、频率等值线、相速度和群速度等探究了波在结构中的传播特性,而且分析了有限尺寸晶格中的弹性波衰减,验证了带隙的存在对弹性波的有效抑制作用。结果表明,该新型结构具备优异的带隙特性,带隙对几何尺寸较敏感,可由此实现带隙的可调性,该新型结构能对1000Hz频率以内的弹性波起到很好的抑制。为低频超材料结构的设计开辟了一条思路。
关键词:低频带隙; 波传播; 振动抑制; 群速度; 相速度
中图分类号:V250.3 文献标识码:A DOI:10.19452/j.issn1007-5453.2024.08.005
基金项目: 航空科学基金(201915048001)
噪声存在于各种工程环境中,而且它对人们的危害很大,为了解决或者降低噪声带来的危害,研究人员经过长久的研究发现可以通过材料的设计来解决这些问题,因此具备噪声和振动控制的材料应运而生,它们也被称为声学超材料[1-2]。尽管在阻声隔振方面的研究有了很大的进展,但是对于低频弹性波的抑制依旧是一个很大的挑战。为了抑制低频振动和噪声,局域共振超材料[3-7]、亥姆霍兹共振超材料[8-9],以及膜型超材料[10-11]等能够有效实现低频衰减的材料,引起了广大研究人员的兴趣。其中,局域共振声子晶体作为典型的声学超材料,具有负等效质量密度[12-14],在声波控制领域具有很好的应用前景。此外,Liu Zhengyou等[15]设计了二维(2D)和三维(3D)声子晶体,突破布拉格散射理论的限制,从而实现低频声波的衰减。Xu Xianchen等[16]通过改变传统的六边形分层蜂窝结构,数值模拟和试验证明了该结构的低频衰减特性。
为了进一步提高低频噪声的衰减,Li Dengke等[17]研究了在微穿孔(MPP)中添加一些延伸管实现低频下更宽的吸声宽带。Lagarrigue等[18]探究了在刚性多孔材料中插入谐振器的周期晶格。Boutin[19]在多孔微结构嵌入多孔基质的阻尼亥姆霍兹谐振器,通过均质化方法讨论了宽带隙和强色散波的出现。Zhou Xiaoling等[20]将多层橡胶和金属圆柱体结合在一起,可以获得多个低频带隙。Thota等[21]提出了一种新型折纸声子结构,研究了该结构的波导和带隙特性。带隙的调谐在隔声减振方面有着非凡的意义。因此,Yang Xiaodong等[22]提出了一种基于参数激励的实时带隙调制技术。Salari-Sharif等[23]通过引入周期性排列的负刚度夹杂物,实现了具有可调谐带隙的超材料。Cai Chengxin等[24]提出了一种调谐局部谐振五模超材料(PMs)第一声子带隙(PGBs)的方法。Peiro-Torres等[25]利用亥姆霍兹谐振器形成的周期结构,说明了共振与带隙之间存在的干扰。另外,具有不同性质的材料在复杂空间结构中不连续分布可能给制造带来巨大挑战[26-31]。为此,Chen Meng等[32-33]使用单相材料设计了具有低频带隙和特定频率范围内双负特性的星形辅助超材料,解决了传统双负声学超材料因其复杂结构和多相材料组成而难以应vhg0JpmluCj31nOj0difxa6wjmhg7wVkKxRbCRkogzw=用的问题。其中,由于特殊的力学性能,手性结构具有独特的振动过滤功能[34]和波转向功能[35],这使得它成为隔声减振的最佳选择之一[36]。此外,Spadoni等[35-36]对六角形手性晶格的声子特性[37-38]进行了全面的研究。研究表明,手性结构在减少声传输和隔振方面具有巨大的潜在优势,其设计灵活性为不同应用中结构声学性能的提高提供了方案。
综上所述,国内外学者使用微穿孔板、星形辅助超材料、手性晶格等结构在低频噪声的隔绝或者衰减方面取得了重大进展,为开发更有效的低频噪声控制技术奠定了基础。本文在前人的基础上继续研究来进一步扩大低频带隙,基于三韧带手性结构提出了一种新型的单相超材料结构,根据数值研究和分析得到拟议结构在0~1000Hz的低频范围内存在多个完全带隙。而常见的三韧带手性结构的第一条带隙的下边缘频率为2164.60Hz,带铰链的三韧带手性结构第一条带隙的下边缘频率为2079.71Hz[39],故新型结构表现出更好的低频降噪性能。本文首先介绍了模型设计和布洛赫(Bloch)定理的相关知识,分析了拟议结构的带隙特性,通过对不同频率的三维色散曲面、群速度、相速度、频率等值线和波传播方向探究了波在结构中的传播特性,然后分析了弹性波在由拟议结构组成的有限晶格尺寸中的动态衰减性能。
1 模型设计
基于三韧带手性结构如图1(a)所示,本文设计了一种新的单相超材料,拟议结构的局部示意图如图1(b)所示,经过旋转变换组成的胞元如图1(c)所示,由于三韧带手性具有很好的拓展性,可以对它的韧带进行延长、重新组合、对称变化等从而得到新的结构。基于这样的思想,对基础三韧带手性结构进行韧带延长和单元结构对称变化可以得到所需要的结构胞元。拟议结构的几何参数:L=42mm,α= 60°,β=60°,R1=4mm,R2=5mm,t=1mm;材料参数:弹性模量为1.75GPa,泊松比为0.4,密度为930kg/m3。
周期结构的晶格常数为L,中心圆环内半径为R1,外半径为R2,结构的厚度设为t,韧带之间的夹角分别为α和β,与圆环连接的三条韧带长度皆为L1,用于连接作用的最外层三条韧带长度分布为L2,L3和L4,根据结构几何尺寸之间的关系,L1可以这样表示
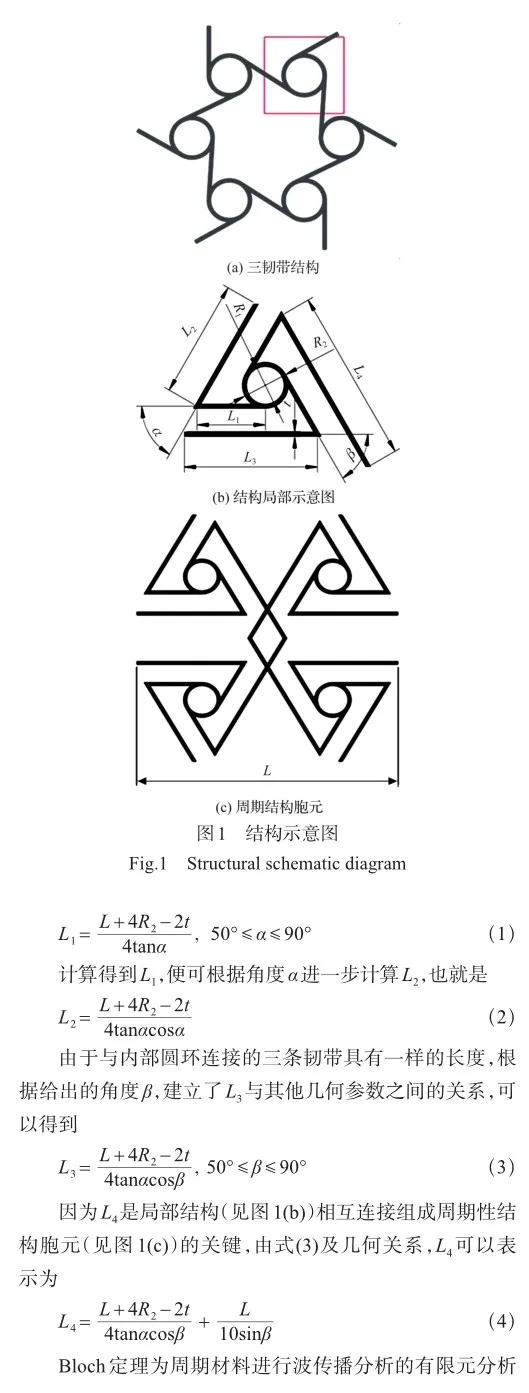

2 数值结果和讨论
本节首先分析了拟议结构的带隙特性和带隙形成机制,并且探究了几何参数对带隙频率范围和位置的影响。分别以群速度、相速度、频率等值线和波传播方向分析了波在结构中的传播特性,最后分析了振动在拟议结构组成的有限尺寸周期结构中的传递特性,进一步验证了带隙的存在对振动的抑制作用。
2.1 能带结构
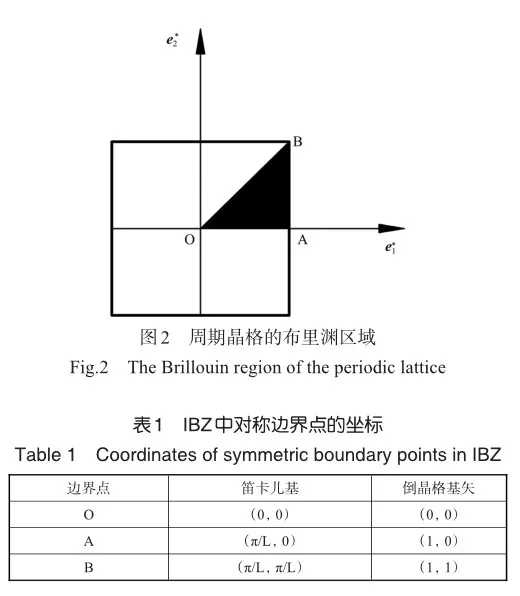
如图3(a)所示,拟议结构被设置为单相超材料结构。为了与由其衍生的局域共振结构进行比较。在此设置了两个对照结构,如图3(b)中黄色区域所示为只带夹杂物(弹性模量为4.08GPa,泊松比为0.42,密度为11600kg/m3)的模型结构,图3(c)为增加包裹材料的模型结构,其中的蓝色区域为软包裹材料(弹性模量为0.4MPa,泊松比为0.47,密度为1340kg/m3)。为了凸显不同结构的带隙的变化,本文将频率范围设置为0~ 1100Hz,在相同的坐标系下分别计算它们的色散曲线。图3(d)为拟议结构的能带结构图,可以很直观地看到这里有5条带隙,范围分别为238.88~242.73Hz、349.07~287.6Hz、438.26~ 560.87Hz、651.14~654.75Hz和759.46~949.51Hz,由此可见,拟议结构在1000Hz以下具备多条带隙,而且最宽的带隙范围达到了190.05Hz,带隙的最低起始频率达到238.88Hz,带隙的范围集中在较高频率可归因于布拉格散射机制。图3(e)为加入夹杂物后的结构的能带图,虽然产生了6条带隙,而且带隙位置大幅度向低频偏移,但是带隙范围明显变窄,带隙的起始频率为201.29Hz,带隙位置向低频偏移是增加夹杂物后,布拉格散射和局域共振机制的耦合作用。图3(f)绘制了同时加入软包裹材料和夹杂物的拟议结构的能带图,该结构产生了5条频率范围很小的带隙,而由下到上的第一条带隙的开始频率为86.175Hz,显然频率更低,充分展示了局域共振机制的低频带隙作用。图3(d)~图3(f)的能带图表明拟议结构相比于其他两个结构,在1000Hz下具备更佳的带隙范围。同时也传达了一个重要的信息,也就是具备局域共振特性的周期性材料可以使得带隙范围向更低频偏移。
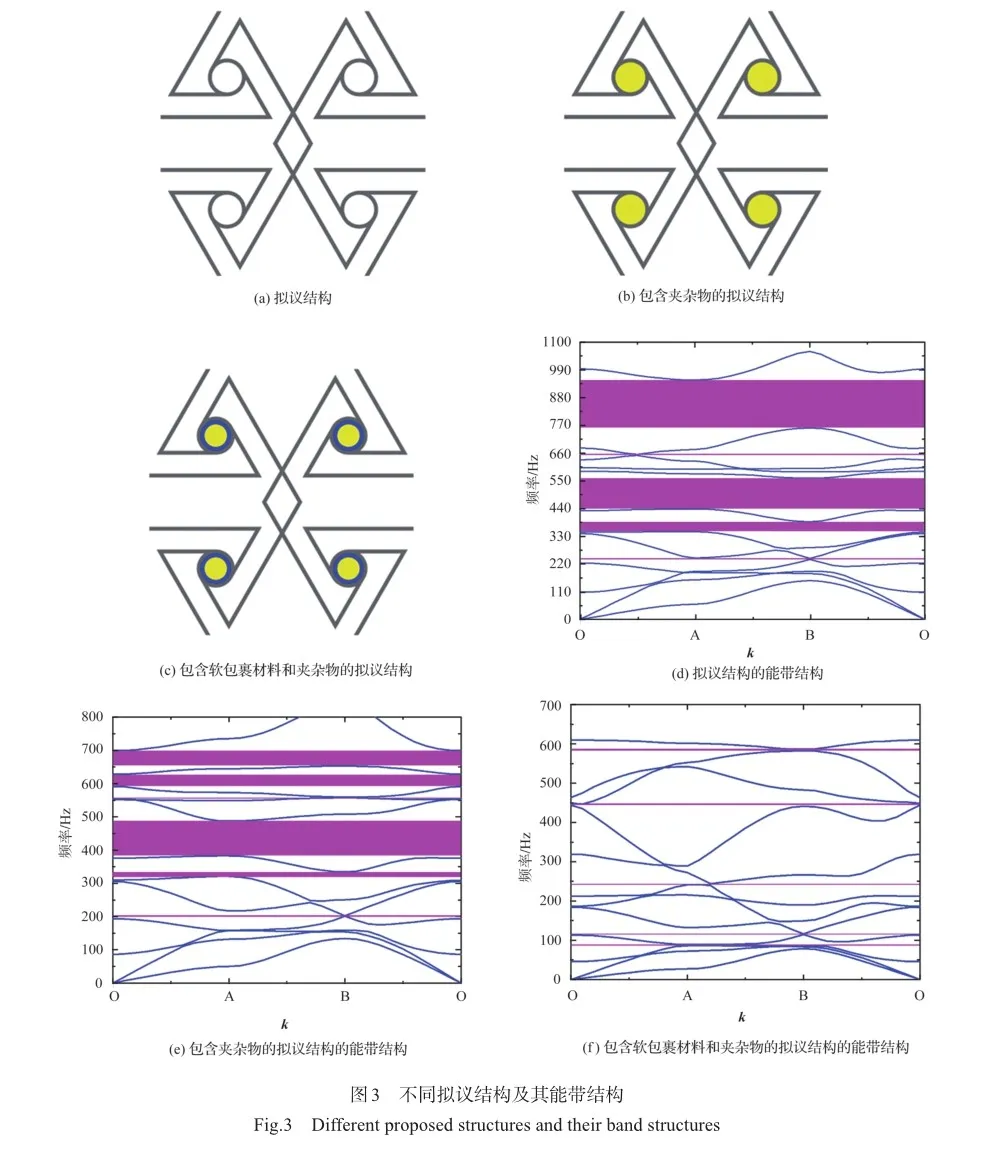
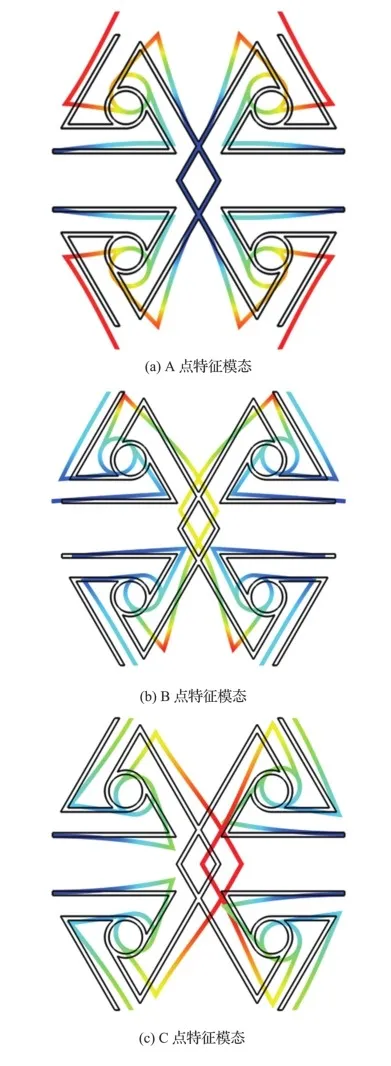
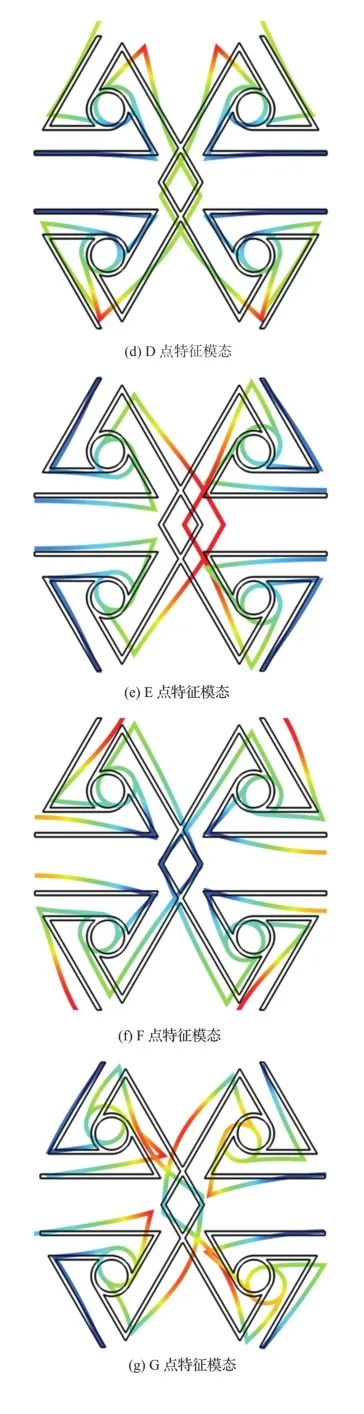
图4(a)的能带结构图提供了关于带隙的一些信息,为了深入了解带隙的形式机制,我们在能带结构图上选取9个点(A~I),然后计算它们对应频率的特征模态。
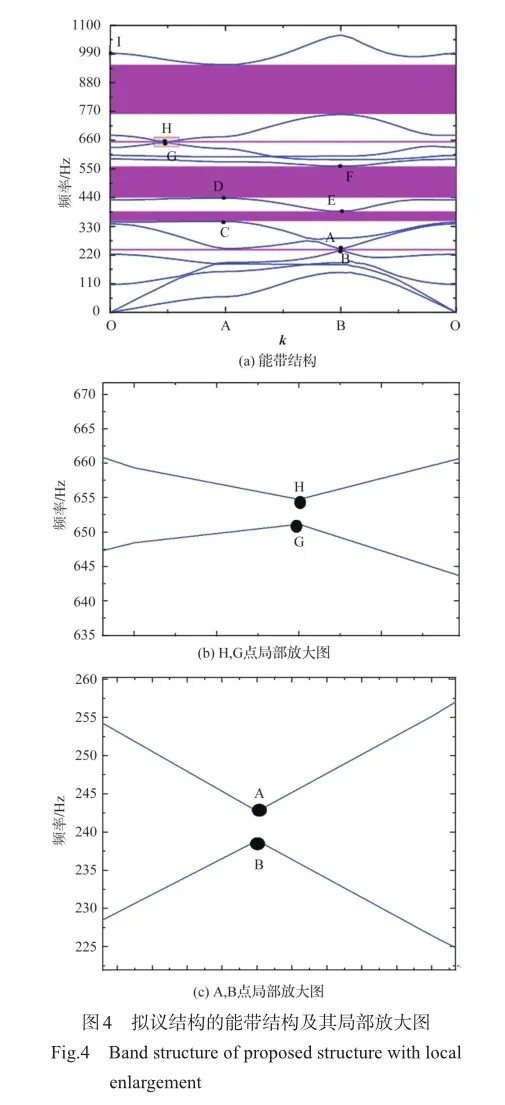
图5(a)、图5(b)为第一条带隙上下边界对应的两个点(A和B)对应的特征模态,它们的共同特点都是在左右形成周期结构的连接韧带位置处几乎没有发生变化,两种的区别是一个振动变形发生在结构的连接韧带部位,而另一个则发生在结构的内部,这样的变化将导致带隙的闭合。图5(c)、图5(d)的特征模态对应点C和D,左右连接韧带依然未发生较大变形,区别在于结构内部的振动变形大小,这两个点所处的通带之间形成了一条带隙。E点的特征模态如图5(e)所示,这里的通带向下弯曲,振动变形表现为结构内部连接韧带的大变形,而图5(f)特征模态的变形SBAtB1lYlNNhBHnVj+Me0lGj7TVi3Wyvg3f+rfUwx6g=集中发生在外连接韧带上,图5(e)、图5(f)这两种变形形式的不同导致二者之间形成了较宽的带隙。G点和H点相应的特征模态的变形形式如图5(g)、图5(h)所示,变形区别依旧是内部连接韧带和外部连接韧带。而且G点的特征模态在内部发生了旋转变形,因此带隙又有将要闭合的趋势。最后一点I的特征模态如图5(i)所示,变形依旧集中于外部连接韧带,与H点的变形形式形成了对比,在两者所处的通带之间形成了一条宽带隙。因此,带隙的形成与结构内外连接韧带的振动变形形式息息相关。

2.2 参数化研究
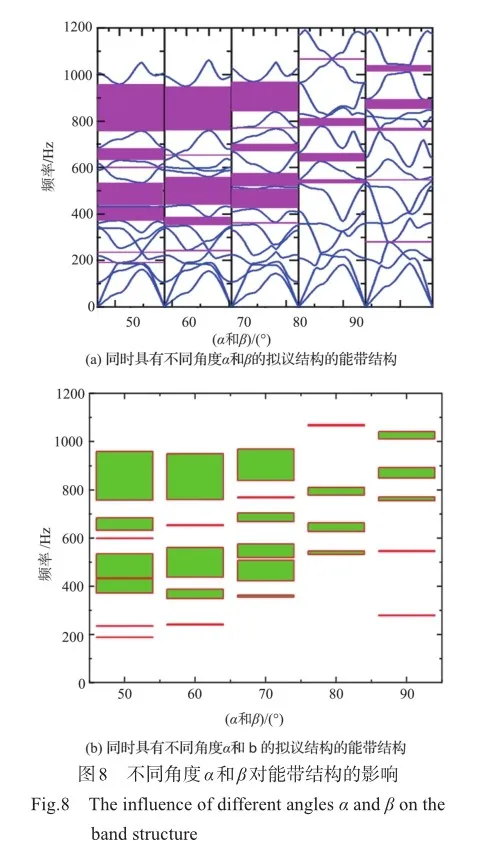
很多研究表明,带隙与结构的几何尺寸有着密不可分的关系,为了适应各种复杂工程的应用,实现带隙的可调性,本文分析了拟议结构韧带间的角度α和β变化时,带隙的位置和范围的改变。在这里分三种情况研究带隙对相应角度的敏感程度:(1)保持β的大小不变,改变α的大小,分析带隙对角度α的依赖性;(2)保持α的大小不变,通过改变β研究带隙的位置和宽度的改变;(3)同时改变α和β的大小,而且使得它们变化的比例相同。计算得到如图6(a)所示具有不同角度α的结构的能带结构,图中粉色阴影是带隙的范围和位置,从图6中可以看出,α对带隙的影响很明显,随着α的增加,带隙表现出先向高频增加后向低频降低的趋势,带隙的数量保持不变,而最明显的是从下到上的第一带隙范围显著增加,同时第4条带隙的宽度也越来越宽。具体角度变化见表2。为了更直观地观察带隙的位置和范围,我们做了如图6(b)所示的浮动柱状图,图中所显示的带隙信息与能带结构一致。α对带隙的显著影响主要是因为角度的变化导致单元几何结构发生变化,对布拉格散射机制的鲁棒性产生了影响。
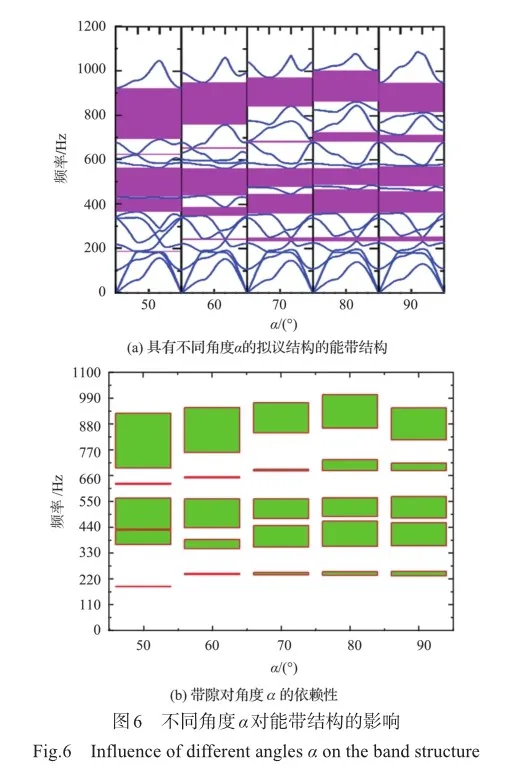
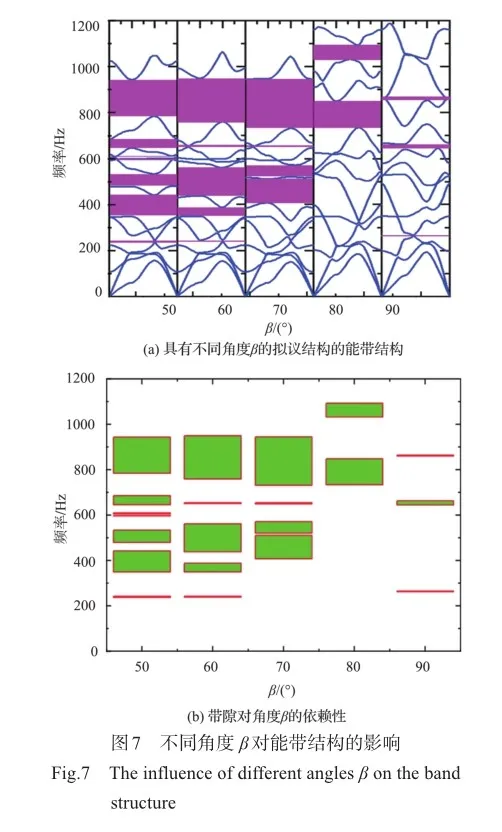
图7(a)描述了具有不同角度β的结构的带隙信息,由图7可知,β同样对带隙有一定的影响,且影响较大,随着角度β的增加,第一条带隙频率范围变小而且在β=70°和β= 80°时,基本为零。同时带隙的总宽度也大幅度减小。相比于α,β对带隙的影响更大,因此,带隙对β的变化较敏感。图7(b)的浮动柱状图与图6(b)表示的意义一样,上边界为带隙的终止频率,下边界为带隙的起始频率,宽度为带隙频率范围的大小,图中更直观地表达了不同位置的带隙信息。β对带隙的影响同样也是因为角度的变化导致单元几何结构发生变化,对布拉格散射机制的鲁棒性产生了影响。
图8(a)为α和β同比例变化时拟议结构的能带结构,显然当两个角度都较小时,带隙的起始频率更低,而且带隙的频率范围更有优势,随着两个角度的增加,带隙逐渐向高频偏移而且带隙的频率范围变窄。由此可知,当两个角度同时变化时,带隙的位置和范围都发生了明显的变化,带隙对α和β的变化极其敏感。图8(b)给出了对应的带隙信息,更加形象地表示了带隙的位置和宽度的变化。
2.3 群速度和波传播
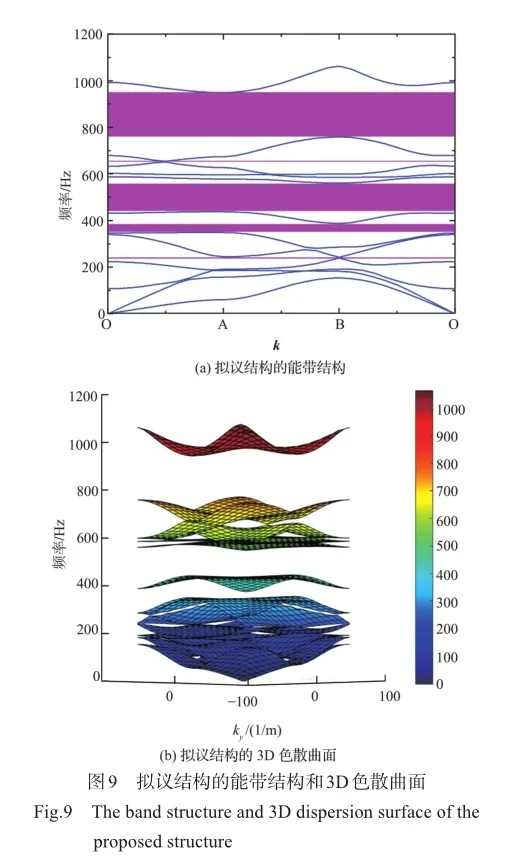
图9(a)和图9(b)绘制了拟议结构的能带结构和3D色散曲面,可以从3D色散曲面上选取特定的色散曲面,分析波的传播特性。此外,群速度是研究弹性波在结构中传播特性的一个重要概念。在二维周期性材料中群速度沿x和y方向可以表示为

群速度表示给定频率下,周期结构的频散特性和平面内波传播的各向异性。因此,可以确定波传播的优先方向或禁止方向。也就是说晶格色散行为的测定可以由某个频率对应的群速度来表示,它描述了平面波传播中的各向异性行为。接下来将分析不同色散曲线上波的传播特性。
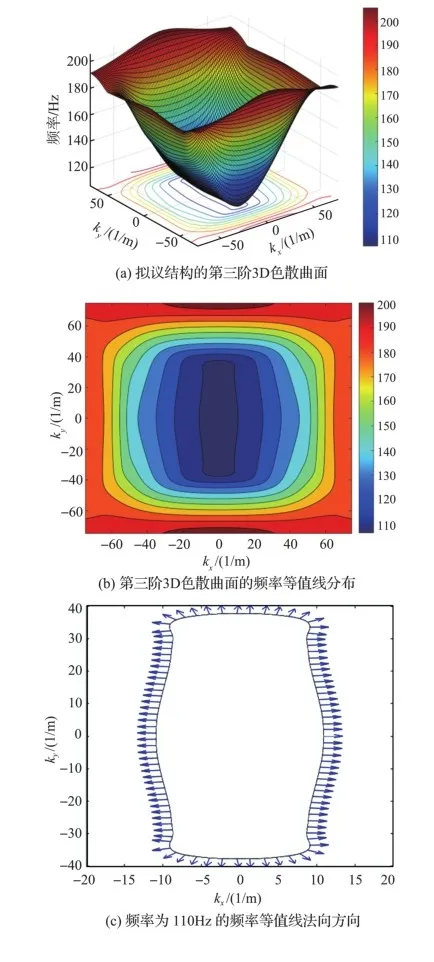
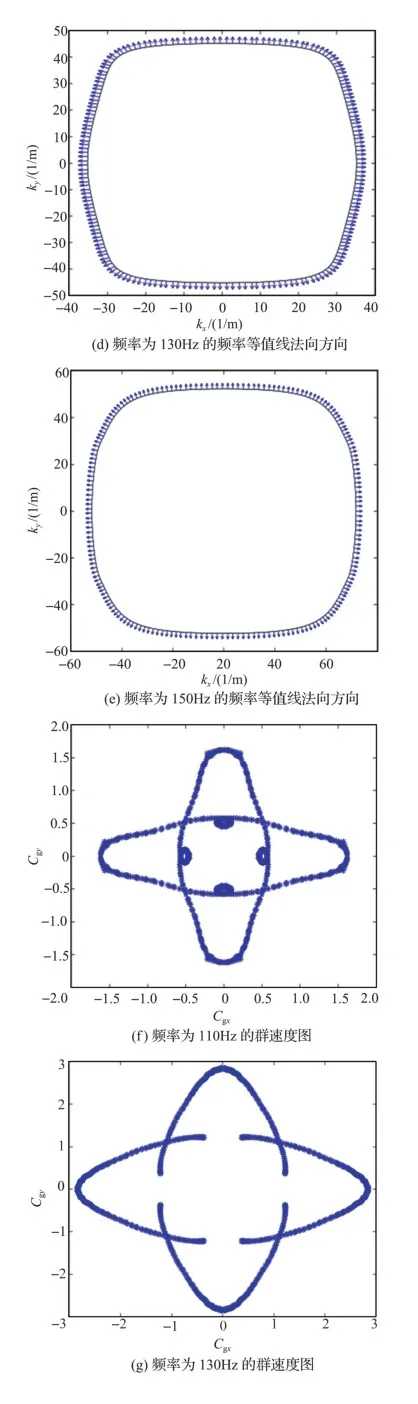
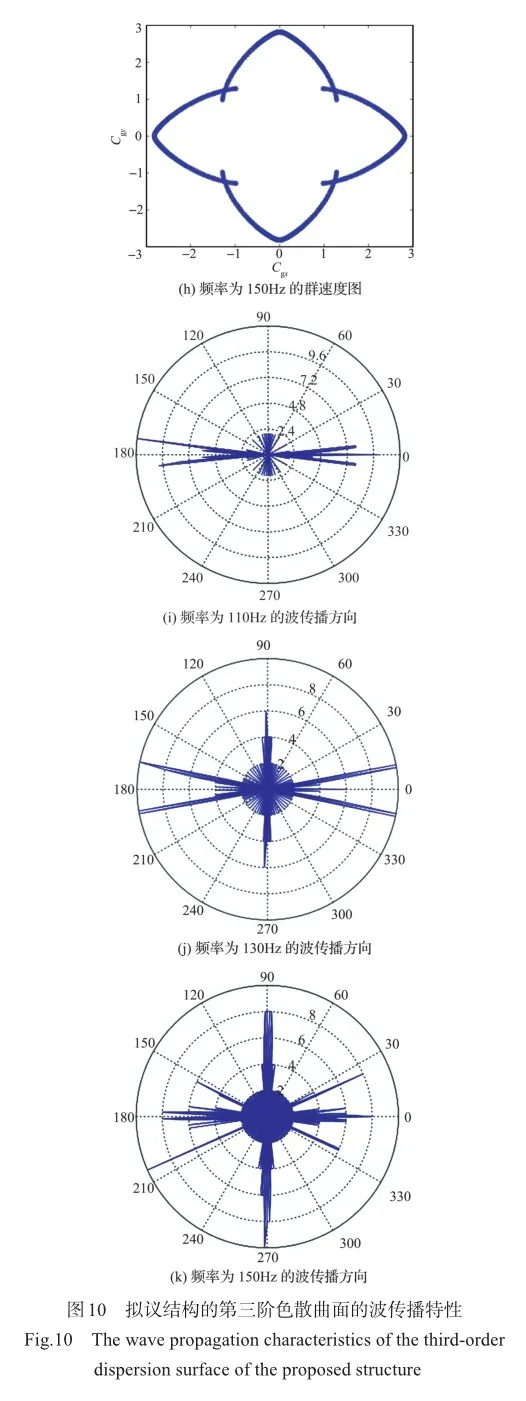
图10(a)和图10(b)分别为第三阶3D色散曲面和对应的频率等值线分布,由频率等值线的强烈各向异性看出,波在水平和垂直方向的变化较大,表现为频率等值线的急剧变化。分别选取频率为110Hz、130Hz和150Hz的特定频率等值线,用来分析波的传播特性。相应的等值线法向方向如图10(c)和图10(e)所示,由图可知,在水平方向和垂直方向的法线方向明显更加密集。这种特性也在图10(f)和图10(h)中以群速度图像的方式得到验证,群速度传达了波的能量聚集在水平和垂直方向上,而在对角线方向形成了振动盲区。图10(i)和图10(k)用极坐标的形式表示波的传播方向和波的传播区域,极坐标中内部的每个圆周上的数字表示落在每个传播区域中的数量,数量越大表示该区域传播的波的能量越大。其特征与等值线法向方向和群速度聚集的方向一致。
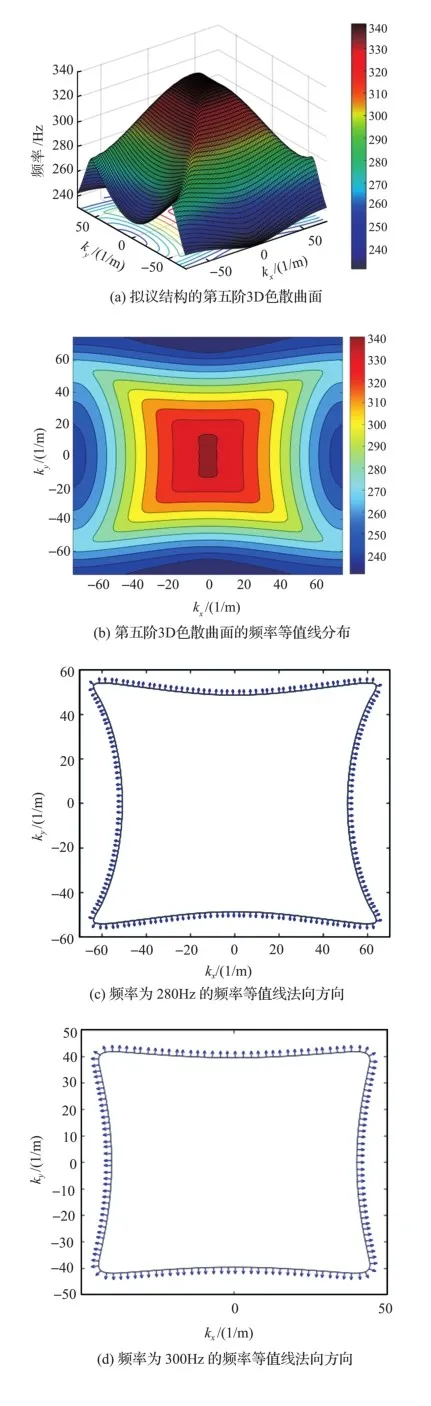
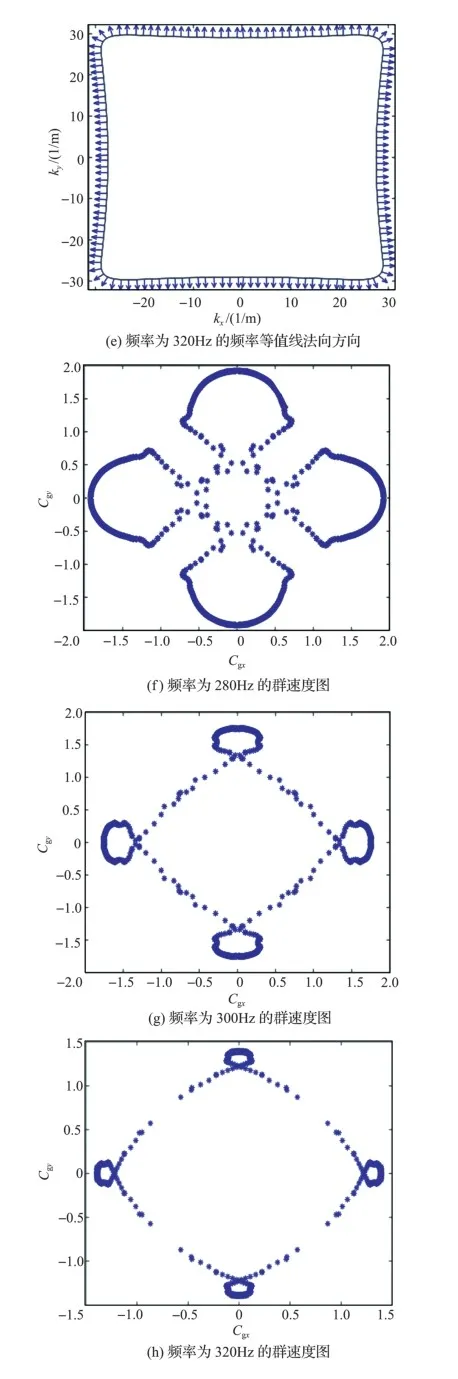
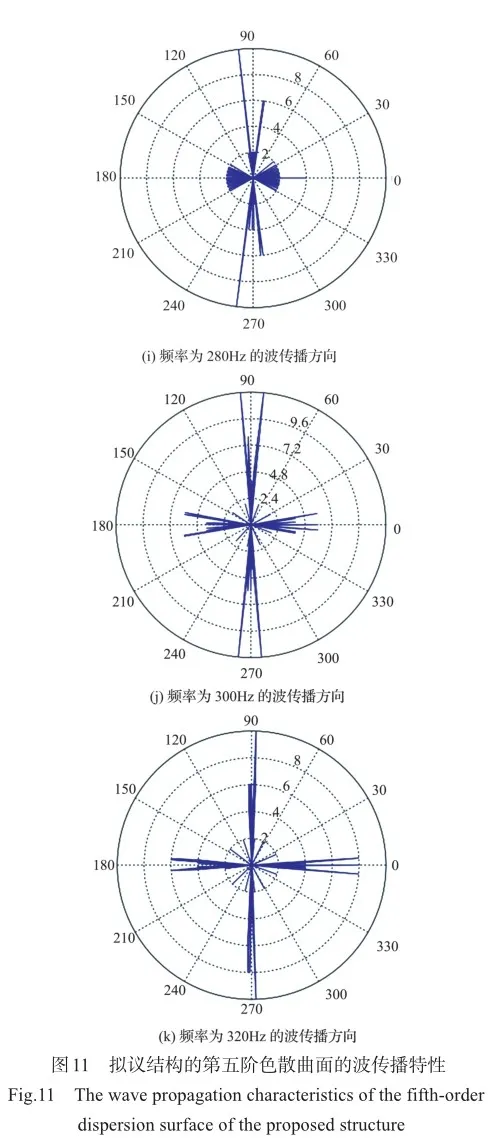
第五阶色散曲面和对应的频率等值线分布如图11(a)和图11(b)所示,频率等值线同样具备强烈的各向异性特性,依旧是在水平方向和垂直方向上频率等值线变化较大,较密集。图11(c)和图11(d)分别为特定频率280Hz、300Hz和320Hz的频率等值线的法线方向、水平方向和垂直方向的分布较密集,而图11(f)和图11(h)为这三个频率对应的群速度,可以明显地发现群速度集中分布在水平方向和垂直方向,而且随着频率的增加群速度开始减小。这意味着波在这两个方向上有较强的能量聚集。在图11(i)和图11(k)中相应频率下的波传播YAQXB+dLRG+LnvRrL3BWe24yggt6h7A5BYW0K0k1sl4=方向和传播区域主要为±90o、0o和180o,进一步表明了波传播具有一定的方向性。
第八阶3D色散曲面如图12(a)所示,相应的频率等值线分布如图12(b)所示,频率等值线在低频时具有强烈的各向异性特性,在高频率时开始呈现出各向同性特性。在此分别取三个相对较高的频率579Hz、580Hz和585Hz,计算得到它们对应的频率等值线的法线方向如图12(c)~图12(e)所示,不难发现它们开始在对角线方向上较密集,随着频率的增加逐渐表现出各向同性。图12(f)~图12(h)为相应频率下的群速度图像,波在对角线的传播能量比较强烈,而在水平方向和垂直方向上群速度分布较少。图12(i)~图12(k)中描述的波的传播方向和区域的表现形式与群速度描述的一致。
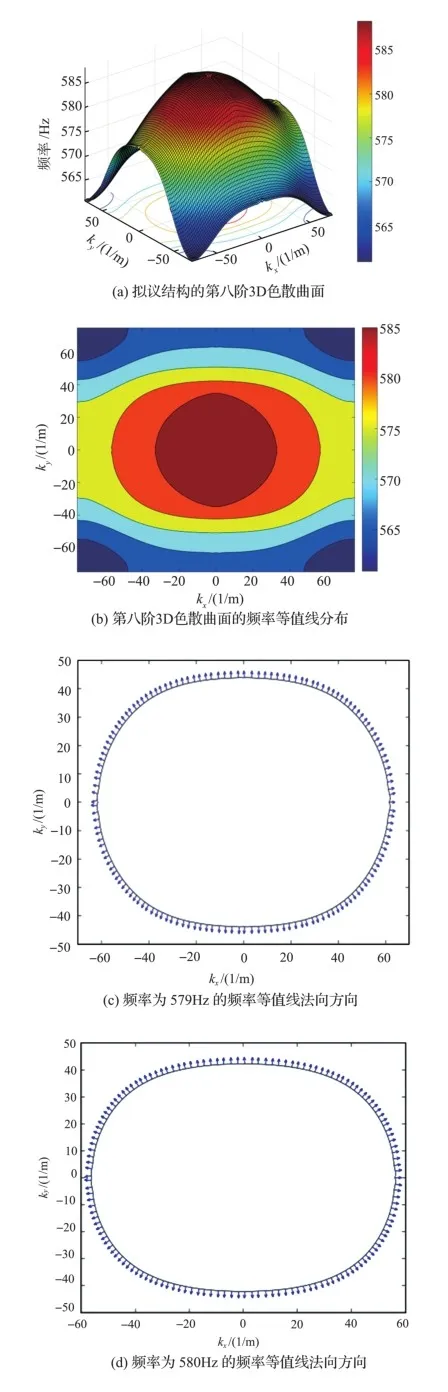
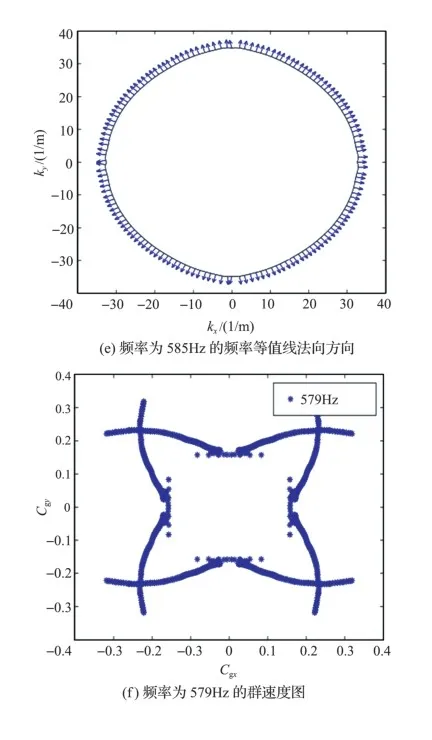

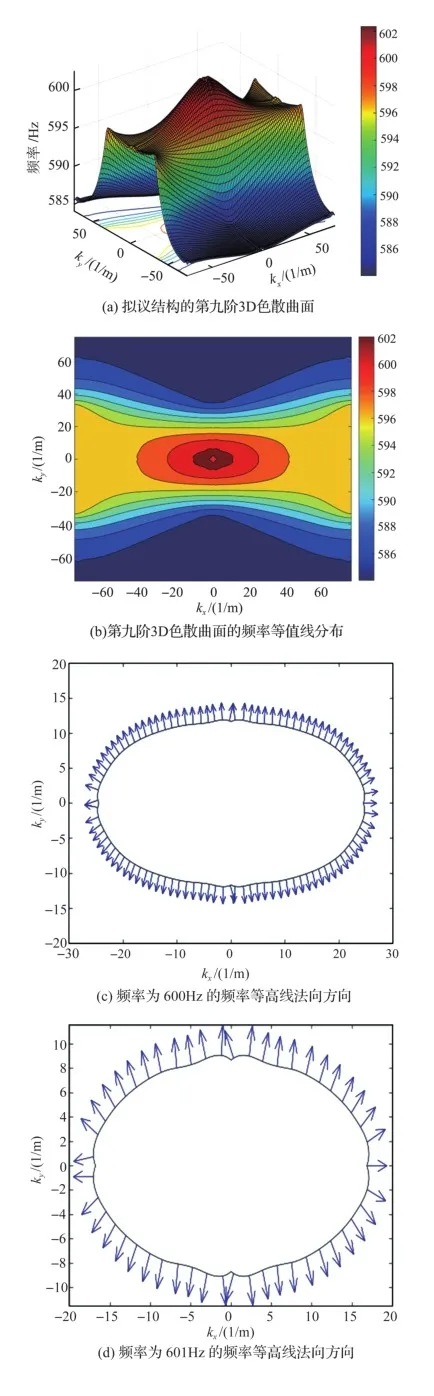
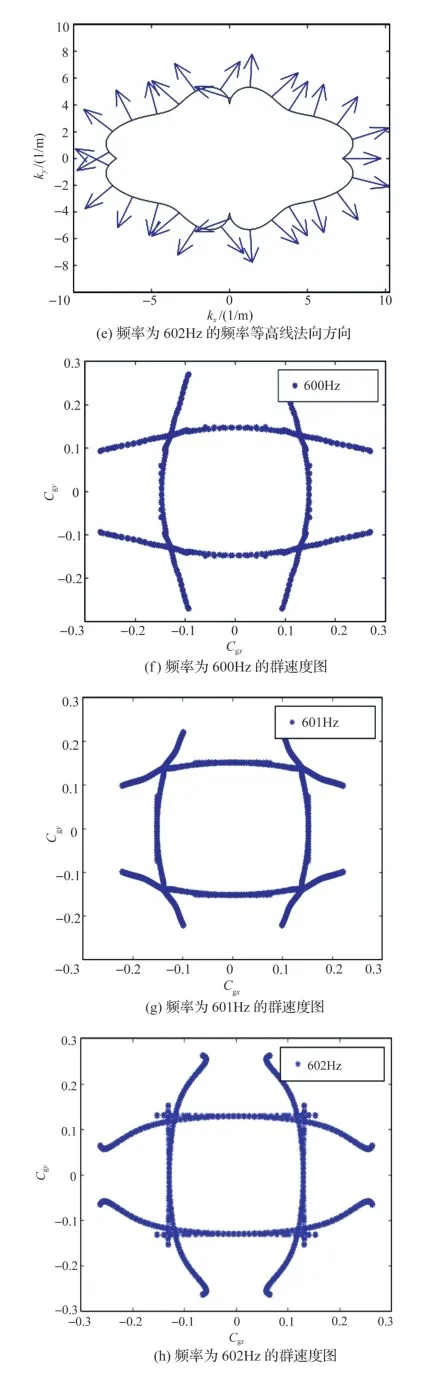

图13(a)、图13(b)是第九阶3D色散曲面和相应的频率等值线分布,由图中看出,在垂直方向上的频率等值线分布较密集而且变化急剧。为了进一步分析波的传播,选取三个频率分别为600Hz、601Hz和602Hz的特定频率等值线,并做出它们的外法线方向以观察波的能量流向,如图13(c)~图13(e)所示,结果法线方向在各个方向皆有分布,不同的是对角线方向的分布比其他两个方向更加密集。图13(f)~图13(h)绘制了这三个频率的群速度图像,群速度在各个方向也都有分布,但是对角线的分布明显较多,这样的传播特征在图13(i)~图13(k)中波的传播方向和传播区域得到体现,在±45°对角线方向波的传播区域较大,与法线方向和群速度描述的一致。
2.4 相速度
相速度是描述波传播特性的另外一个重要概念,相速度即弹性波相位传播的速度波矢k 决定相速度的方向。在倒空间中,波矢的表达如式(14)所示,即给定某一频率的弹性波的相速度可以这样表示

计算相速度时,选择特定的频率和与频率对应的波矢。然后,根据式(18)计算相速度的大小和方向。对于二维的各向同性介质,弹性波在0°~360°范围内均匀传播,表明相速度在各个方向上的传播速度是相同的。相反地,各向异性介质的相速度曲线不再是圆形,在一些方向上相速度值较大,而在其他方向上相速度的值偏小,此时相速度曲线为有凸起或凹陷的多边形。
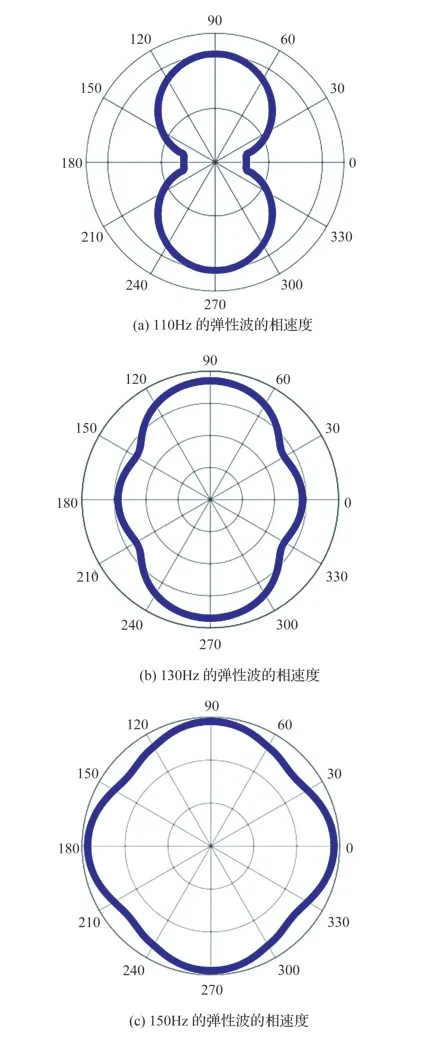
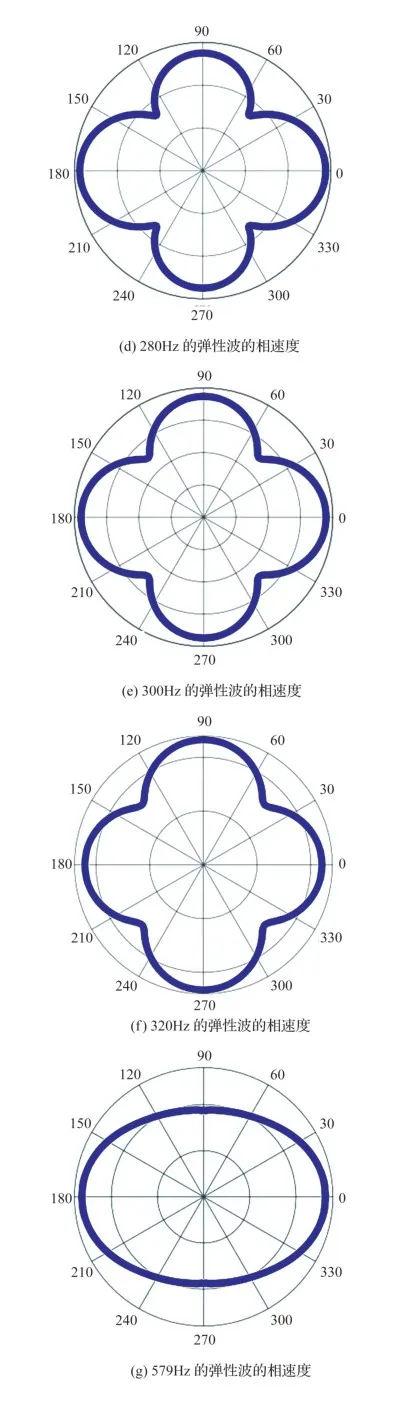
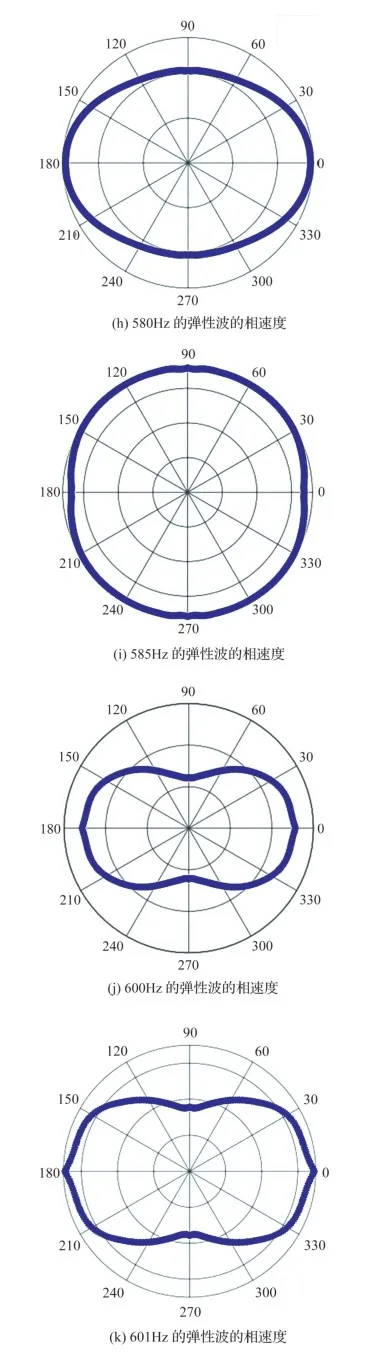
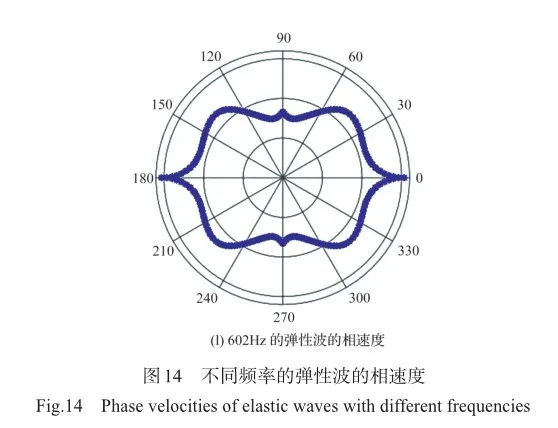
弹性波的色散特性需要群速度和相速度进行对比分析,为此我们选取与群速度一样的频率来计算相速度。由图14(a)、图14(b)可知,在频率为110Hz和130Hz时,弹性波在±90o方向的相位传播具有优先权。频率为150Hz时弹性波不仅在±90o方向具有优先权,而且在0o和180o方向上较突出。图14(d)~图14(f)的三个相速度图像具有一样的特性,都是在±90o、0o和180o方向上传播较快。如图14(g)~图14(i)所示,频率为579Hz、580Hz和585Hz时,相速度的传播由0o和180o方向转向±90o方向。图14(i)~图14(l)的相速度图像显示了相反的特性,同样表现出强烈的各向异性特性,而且在0o和180o方向上弹性波的相位传播最快。相速度值的大小与频率大小呈正相关,但是相速度的方向不具有规律性。综上所述,相速度的大小和方向与频率的大小息息相关。
3 振动在有限尺寸周期晶格中的传播
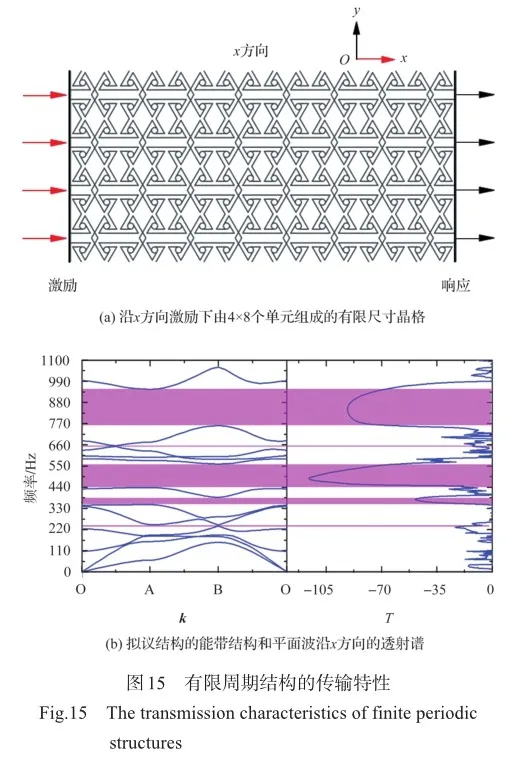
本文通过有限元方法探讨了拟议结构的色散关系和简单的传波信息。为了进一步验证拟议结构的动力学行为,我们构建了由拟议结构组成的有限尺寸周期晶格来研究有限周期晶格中的振动传输行为。在此我们从x方向施加激励,也就是在输入端施加频率为0~1100Hz的入射平面波,在相应的另一侧接受响应。而频率响应函数的透射谱可以用无量纲函数来表示,也就是透射系数T

为了进一步说明由拟议结构组成的有限尺寸周期晶格在相应的频率范围内具备的特定抑波特性。我们分别选择不同阶段的频率,即在通带内选取频率为300Hz,在带隙内选取频率为880Hz。激励的施加如图15(a)所示,频率为300Hz的平面波作用下的有限尺寸周期晶格的变形如图16所示,按照给出的位移变形颜色比例,在整个有限尺寸周期晶格中发生的变形很显著,表明振动的传输穿过了整个周期结构。而在带隙频率范围内选取的频率为880Hz,显然变形仅发生在有限尺寸周期晶格的激励边界附近,即频率为880Hz的平面波在结构中受到明显抑制(见图17)。这两种不同的传输特征表明处于通带内和带隙内振动传输的差异。

4 结论
本文基于三韧带手性结构提出了一种新型的二维单相超材料结构,数值分析了拟议结构的带隙特性和带隙形成机制,然后探讨了波传播特性和有限尺寸周期晶格中振动的动态传递行为,经过分析和数值研究,得出以下结论:
(1)拟议结构在1000Hz的频率范围下能够产生多个带隙,带隙优于由该结构衍生的局域共振性结构。
(2)带隙依赖于拟议结构连接韧带之间的夹角α和β的变化,而且带隙不仅对β的变化较敏感,还对α和β同比例变化也十分敏感,可通过改变几何参数来实现带隙的可调性。
(3)波在结构中的传播具有一定的方向性,频率的大小对波的传播方向和传播区域都有影响。通过对有限尺寸周期晶格中的振动传输的动态模拟,得到的传输透射谱与带图中的带隙信息完美匹配。验证了带隙频率范围内的激励会受到明显的抑制,表明了拟议结构潜在的减振降噪性能。
参考文献
[1]Hussein M I, Leamy M J, Ruzzene M. Dynamics of phononic materials and structures: historical origins, recent progress, and future outlook[J]. Applied Mechanics Reviews, 2014, 66(4): 040802.
[2]Maldovan M. Sound and heat revolutions in phononics[J]. Nature, 2013, 503(7475): 209-217.
[3]Graczykowski B, Alzina F, Gomis-Bresco J, et al. Finite element analysis of true and pseudo surface acoustic waves in one-dimensional phononic crystals[J]. Journal of Applied Physics, 2016, 119(2): 025308.
[4]丁昌林, 史剑兵, 董仪宝,等. 一种双频和宽频超表面材料的探索研究[J]. 航空科学技术, 2022,33(5):76-81. Ding Changlin, Shi Jianbing, Dong Yibao, et al. Exploratory research on a dual-band and broadband metasurface materials[J]. Aeronautical Science & Technology, 2022,33(5):76-81.(in Chinese)
[5]Tol S, Degertekin F L, Erturk A. Gradient-index phononic crystal lens-based enhancement of elastic wave energy harvesting[J]. Applied Physics Letters, 2016, 109(6): 063902.
[6]Xu Jincheng, Wu Zhengzhong. Lamb waves in binary locally resonant phononic plates with two-dimensional lattices[J]. Applied Physics Letters, 2007, 90(20): 201904.
[7]Khelif A, Achaoui Y, Benchabane S, et al. Locally resonant surface acoustic wave band gaps in a two-dimensional phononic crystal of pillars on a surface[J]. Physical Review B Condensed Matter, 2010, 81(21):1601-1614.
[8]Nicholas F, Xi Dongjuan, Xu Jianyi, et al. Ultrasonic metamaterials with negative modulus[J]. Nature Materials, 2006, 5(6):452-456.
[9]梁春华,孙广华. 商用飞机发动机先进降噪技术[J]. 航空科学技术, 2011,22(4): 48. Liang Chunhua, Sun Guanghua. Advanced noise reduction technology for large commercial aircraft engines[J]. Aeronauti‐cal Science & Technology, 2011,22(4): 48.(in Chinese)
[10]Yang Zhiyu, Mei Jun, Yang Min, et al. Membrane-type acoustic metamaterial with negative dynamic mass[J]. Physical Review Letters, 2008, 101(20): 204301.
[11]Zhou Weijian, Wu Bin, Muhammad G, et al. Actively tunable transverse waves in soft membrane-type acoustic metamaterials[J]. Journal of Applied Physics, 2018, 123(16):165304.
[12]Liu Zhengyou, Zhang Xixiang, Mao Yiwei, et al. Locally resonant sonic materials[J]. Science, 2000, 289(5485): 1734-1736.
[13]Meng Hao, Wen Jihong, Zhao Honggang, et al. Optimization of locally resonant acoustic metamaterials on underwater sound absorption characteristics[J]. Journal of Sound and Vibration, 2012, 331(20): 4406-4416.
[14]Wang Yanfeng, Wang Yuesheng. Complete bandgaps in twodimensional phononic crystal slabs with resonators[J]. Journal of Applied Physics, 2013, 114(4): 043509.
[15]Liu Zhengyou, Chen Ziting, Sheng Ping. Analytic model of phononic crystals with local resonances[J]. Physical Review B, 2005, 71(1):014103.
[16]Xu Xianchen, Miles V, Li Xiaopeng, et al. Tailoring vibration suppression bands with hierarchical metamaterials containing local resonators [J]. Journal of Sound and Vibration, 2019, 442: 237-248.
[17]Li Dengke, Chang Daoqing, Liu Bilong. Enhancing the low frequency sound absorption of a perforated panel by parallelarranged extended tubes[J]. Applied Acoustics, 2016, 102: 126-132.
[18]Lagarrigue C, Groby J P, Tournat V, et al. Absorption of sound by porous layers with embedded periodic arrays of resonant inclusions[J]. Journal of the Acoustical Society of America, 2013, 134(6): 4670-4680.
[19]Boutin C. Acoustics of porous media with inner resonators[J]. Journal of the Acoustical Society of America, 2013, 134(6): 4717-4729.
[20]Zhou Xiaoling, Xu Yanlong, Liu Yu. Extending and lowering band gaps by multilayered locally resonant phononic crystals[J]. Applied Acoustics, 2018, 133: 97-106.
[21]Thota M, Wang K W. Tunable wave guiding in origami phononic structures[J]. Journal of Sound and Vibration, 2018, 430: 93-100.
[22]Yang Xiaodong, Cui Qingdian, Qian Yingjing, et al. Modulating band gap structure by parametric excitations[J]. Journal of Applied Mechanics, 2018, 85(6):061012.
[23]Salari-Sharif L, Haghpanah B, Izard A G, et al. Negative-stiff‐ness inclusions as a platform for real-time tunable phononic metamaterials[J]. Physical Review Applied,2019,11(2): 024062.
[24]Cai Chengxin, Han Chao, Wu Jianfeng, et al. Tuning method of phononic band gaps of locally resonant pentamode metamateri‐als[J]. Journal of Physics D:Applied Physics, 2018, 52(4): 045601.
[25]Peiro-Torres M P, Castineira-Ibanez S, Redondo J, et al. Interferences in locally resonant sonic metamaterials formed from Helmholtz resonators[J]. Applied Physics Letters, 2019, 114(17):171901.
[26]Bandyopadhyay A, Heer B. Additive manufacturing of multimaterial structures[J]. Materials Science and Engineering: Reports, 2018, 129:1-16.
[27]Chen Da, Zheng Xiaoyu. Multi-material additive manufacturing of metamaterials with giant, tailorable negative poisson’s ratios[J]. Scientific Reports, 2018, 8(1):9139.
[28]Abueidda D W, Jasiuk I, Sobh N A. Acoustic band gaps and elastic stiffness of PMMA cellular solids based on triply periodic minimal surfaces[J]. Materials & Design, 2018, 145: 20-27.
[29]Franziska W, Maximilian W, K?rner C. Single phase 3D phononic band gap material[J]. Scientific Reports, 2017, 7(1): 3843.
[30]Fei Xiang, Jin Lei, Zhang Xiujuan, et al. Three-dimensional anti-chiral auxetic metamaterial with tunable phononic bandgap[J]. Applied Physics Letters, 2020, 116(2):021902.
[31]Huang Yilan, Li Jian, Chen Weiqiu, et al. Tunable bandgaps in soft phononic plates with spring-mass-like resonators[J]. International Journal of Mechanical Sciences, 2019, 151: 300-313.
[32]Chen Meng, Xu Wenshuai, Liu Yu, et al. Band gap and doublenegative properties of a star-structured sonic metamaterial[J]. Applied Acoustics, 2018, 139: 235-242.
[33]Chen Meng, Jiang Heng, Zhang Han, et al. Design of an acoustic superlens using single-phase metamaterials with a starshaped lattice structure[J]. Scientific Reports, 2018, 8(1):1861.
[34]Martinsson P. G. Vibrations of lattice structures and phononic band gaps[J]. Quarterly Journal of Mechanics & Applied Mathematics, 2003, 56(1):45-64.
[35]Spadoni A, Ruzzene M, Gonella S, et al. Phononic properties of hexagonal chiral lattices[J]. Wave Motion, 2009, 46(7): 435-450.
[36]Hussein M I, Leamy M J, Ruzzene M. Dynamics of phononic materials and structures: historical origins, recent progress, and future outlook[J]. Applied Mechanics Reviews, 2014, 66(4): 040802.
[37]Spadoni A, Ruzzene M, Gonella S, et al. Phononic properties of hexagonal chiral lattices[J]. Wave Motion, 2009, 46(7): 435-450.
[38]Spadoni A, Ruzzene M. Structural and Acoustic behavior of chi‐ral truss-core beams[J]. World Academy of Science Engineering& Technology, 2006, 128(5): 616-626.
[39]Tan Wangxi, Su Xunwen, Zhu Dongmei, et al. Band gap adjust‐ment of an improved three-ligament chiral structure with flex‐ure hinges[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2022, 44(8): 341.
Study of Low-frequency Band Gaps and Vibrational PrmJvgKgvaqYNO1Qv4fQ+9o9oWm2UNU3GLnu7XScQ7bKQ=operties in Novel Monophasic Metamaterials
Yang Hongyun1, Zhang Zhaozhan2, Wang Shuo2, Yan Hao3, Ding Qian2, Dong Xingjian4,
Sun Yongtao2, Yan Qun3
1. State Key Laboratory of Metastable Materials Preparation Technology and Science, Yanshan University,Qinhuangdao 066004, China
2. Tianjin Key Laboratory of Nonlinear Dynamics and Control, Tianjin University, Tianjin 300350, China
3. Aircraft Strengthes Research Institute of China, Xi’an 710065, China
4. State Key Laboratory of Mechanical Systems and Vibration, Shanghai Jiao Tong University, Shanghai 200240,China
Abstract: Low frequency vibration and noise suppression has always been a problem that needs to be overcome. Therefore, a novel single-phase metamaterial structure is proposed in this paper. Based on Bloch’s theorem and finite element method, the bandgap characteristics and formation mechanism of the proposed structure are numerically analyzed, and the dependence of the bandgap on geometric size is parameterized. The propagation characteristics of waves in the structure are explored using three-dimensional dispersion surfaces, frequency contours, phase velocity, and group velocity, Moreover, the attenuation of elastic waves in finite size lattices was analyzed, verifying the effective suppression effect on band gaps on elastic waves. The results indicate that the proposed structure has excellent bandgap characteristics, and the bandgap is sensitive to geometric dimensions, which can achieve tunable bandgap. The proposed structure can effectively suppress elastic waves within a frequency range of 1000Hz. It provides important clues and ideological guidance for the design of devices with low-frequency vibration isolation performance.
Key Words: low frequency bandgap; wave propagation; vibration suppression; group velocity; phase velocity

