高校新文科建设中数理模型简化问题研究

【摘 要】 当前许多文科领域在研究方法上越来越倾向于借助定量数理模型开展前沿研究，然而文科学习者和实务工作者数理工具基础相对薄弱，造成研究与教学和应用之间严重脱节。文章通过一个关于数理模型简化路径的思维框架发现，相对于自然语言模型、全模型、解说式模型、玩偶模型和数值模拟，数值示例可以大大降低文科数理工具门槛，同时保持科学研究的逻辑性、主要思想和发现，可以大幅度拉近“研、教、学、用”的距离。文章提出了数值示例开发的标准流程，同时认为推动数值示例开发一方面需要高素质专业学者队伍的参与，也需要相应的学术环境和资源配套。

【关键词】 新文科；数值示例；理论模型；数理工具

【中图分类号】 G640 【文章编号】 1003-8418（2024）10-0053-08

【文献标识码】 A 【DOI】 10.13236/j.cnki.jshe.2024.10.007

【作者简介】 秦文佳（1978—），女，江苏无锡人，南京大学社会学院博士生，上海财经大学公共经济与管理学院副教授；张熠（1983—），男，山西长治人，上海财经大学公共经济与管理学院教授、博士生导师、经济学博士（通讯作者）。

自20世纪50年代开始，不少人文社会学科开始大量借鉴自然科学研究中的定量研究方法，一方面更加注重通过数学理论模型进行逻辑演绎，阐述学术思想和发现，另一方面更加注重通过数理统计方法，利用数据对理论进行验证。这种趋势起源于经济学，随后也影响了社会学、政治学、管理学等许多学科，成为新文科特征之一。

数学工具的使用产生了两方面效果：从积极的方面来看，大量模糊复杂的现实问题能够高度抽象概括为精炼的数学逻辑问题，使得各项讨论都更加深入细致，大大促进了文科的发展和科学化进程［1］；从消极的方面来看，文科学习者和相关实务部门数理基础总体偏低，随着阅读、了解和掌握前沿研究成果的门槛不断提高，研究、讲授、学习和应用之间的距离拉大。这导致了几个消极的后果：一是教学难度提高，最新的、更深刻的研究发现和思想成果难以走入本科生的课堂，教学和研究之间存在脱节；二是学生面临的学习门槛过高，大量时间和精力需要消耗在数理工具的掌握上，挤压了真正用来思考探索问题的时间和精力［2］［3］；三是学术研究门槛提高，导致研究中更注重形式上的严谨性，而非思想上的创新性和突破性，研究选题范围受到很大限制，一些重大但不适合数理化的现实问题被有意地忽略［4］［5］［6］；四是影响了交叉学科发展和跨学科合作，相对数理基础要求低的学科难以理解数理基础成熟学科的发现，后者也无法将前者的思想成果都予以抽象化、数理化；五是束缚了前沿学术思想更大范围的传播，影响学术成果的推广，当实务界迫切希望学术界能提供可应用的理论指引时，却又难以阅读和理解前沿研究成果发现［7］。

本文认为在新文科建设中解决上述问题并不是要求前沿研究者刻意降低数理工具的应用，而是可以通过数值示例的开发来沟通前沿研究与“教、学、用”之间的联系，这对于提升我国文科的国际学术竞争力，促进前沿成果转化应用是极为有利的。本文以社会保障经济学为例，主要探讨数值示例开发的具体内涵、理论和现实意义以及所需要的条件和学术环境。

一、理论模型简化路径

（一）“全模型”与“自然语言模型”

与自然科学类似，通过数理工具进行社会科学研究，通常要求数理模型具有三个特点：一是严谨性，即数学推导的过程必须建立在精确的逐步逻辑分析上，没有逻辑上的跳跃和模糊，这有助于清晰地刻画变量之间的逻辑传导过程；二是完整性，即模型能够抽象概括研究问题的全部重要方面，模型中未分析的外生变量不会干扰模型主要机制、发现和结论；三是一般性，模型的假设条件尽可能地放松，能够适用于大多数的情形，结论不依赖于特定的参数取值，具有很强的外推性。为了叙述方便，本文中将这种具有严谨、完整和一般性的模型称为“全模型”，对应于图1中的A点。

全模型尽管能够严谨地分析变量之间相互关系和彼此影响过程，但通常变量众多，推导计算复杂，需要掌握不少高等数学技巧。在教学实践中，直接向听众介绍全模型不仅教学时间长，过程较为乏味，也意味着教学要更加深入浅出、循循善诱，这对教师教学水平也提出了很高的要求。“全模型”相对比较适合于研究者同行交流以及面向博士二年级以上同学的课程，并且内容应是听众非常感兴趣的重要问题。

与全模型相对应的是完全用日常生活语言来解释变量之间关系，同样为了表述方便，在本文中称之为“自然语言模型”，对应于图1中的B点。自然语言模型完全或基本不使用数学工具，模型的传导机制以通俗而形象的语言来描述，对模型的严谨性、完整性和一般性都没有硬性的要求，多数的科普著作都使用这种语言。

自然语言模型比较适合面向非专业人士，侧重于介绍一个理论最主要的发现、结论和基本的逻辑演绎思路。自然语言模型虽然较为通俗，容易使读者初步理解或受到启发，但是失去了对变量间相互传导机制的完整展示，缺乏对假设前提和演绎证明过程的精确表述，所得结论的适用边界不够清晰，容易让读者产生“似是而非”“似懂非懂”的感觉。甚至相当一部分思想较为深邃的研究很难通过自然语言就让读者领会其中的精妙之处，导致这些研究成果传播范围受限，没有能够转化为现实可应用的知识。

因此，无论“全模型”还是“自然语言模型”都存在比较大的问题，前者过于专业，导致适应受众很小，而后者过于通俗，导致适应这种方式的知识面很小。因此，拉近“研、教、学、用”的距离必须要对全模型进行适度简化，降低数学和理解上的难度，或对自然语言进行适度严谨化，更好地展示逻辑传导过程。

（二） 理论模型简化路径

根据“全模型”的三个特点即严谨性、完整性和一般性，也就演化出了三种不同的简化路径。

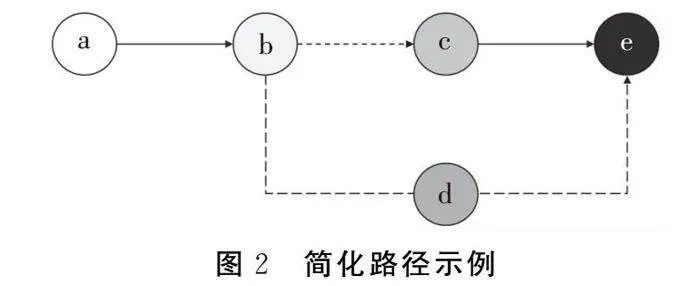
第一条路径是“解说式模型”（illustrative model）。相对于全模型，“解说式模型”不强调机制的严谨性，可以允许部分逻辑环节存在缺失、模糊和跳跃，对应于图1中的C点。举个例子来说，如图2所示，假设全模型拟研究的问题是变量a如何影响到变量e，其中主要的路径是从a到b再影响c，最终导致e。如果b到c的环节较为复杂，那么解说式模型可以较模糊地用自然语言来阐述这个环节，而先用较精确的数学语言来阐述变量a如何影响到变量b以及变量c如何影响变量e。

那么是否意味着从变量b到变量c的环节就不重要呢？通常来说并非如此。恰恰相反，变量b和c之间的关联可能正是整个研究的重点。解说式模型只是为了先“扫除外围”，将听众和读者的注意力引导到最后这个核心机制上来，作者随后会在全模型中对此进行更严谨的分析。

第二条路径是“玩偶模型”（toy model）。相对于全模型，“玩偶模型”不强调完整性，通常是选取了模型中最核心的机制，加以高度抽象凝练。但是，玩偶模型本身传导机制仍是清晰的，获得结论的可推广性也是可以保证的，对应于图1中的D点。举例而言，在图2中，除“a-b-c-e”这条主要机制外，还有一条变量b通过变量d再到变量e的次要机制。玩偶模型可以假设变量d外生，从而关闭这个次要机制，为理论分析营造一个纯净的思想实验环境，集中将主要机制分析清楚。

玩偶模型的特点是只选取了理论最重要的逻辑传导路径，但是要保证这个传导路径是畅通的，尽量避免模糊、缺失和跳跃的环节。在“玩偶模型”之后，研究者可以将更多外生变量或机制打开，以验证和说明即便在更完整的模型下，核心机制和结论也是成立无虞的。这种方式也有助于引导受众重点关注模型的主要机制，迅速理解和把握理论模型的核心思想和发现。例如，在经济学模型中，一旦模型包括不确定性、异质性、一般均衡效应以及动态结构，通常都不再有显式解，因而也就很难完整展示理论机制。所以如果这些结构只是为了完整地展示所有变量之间的关系，而不是核心机制，那么玩偶模型中就可以通过剔除这些效应，获得显式解。

第三条路径是“数值模拟”。数学模型的难度常常是由对一般性的追求导致的，表现在两个方面：一是代数的运用使得模型更为抽象，与现实问题有很大距离，直观理解变得更加困难；二是假设过于一般化导致变量维度和数学处理难度提高。以经济学为例，在效用函数假设中，对数和平方根效用函数相对简单，但是“常相对风险厌恶系数效用函数”则复杂许多，而“Epstein-Zin效用函数”［8］更为一般化，也更复杂。在生产函数假设中，从线性函数到“柯布-道格拉斯生产函数”，再到常替代弹性生产函数，最后到变替代弹性生产函数，也是越来越一般化，但数学上难度也不断增加。因此，一种简化的思路是抛开抽象的数学模型，而代之以具体的数值，对应于图1中的E点。在图2中则意味着变量a、b、c、d、e都不是抽象的代数，而是具体的数值。近年来，不少经济学理论研究在数理模型推导后会给出数值模拟结果。这种数值模拟使得模型从一般抽象到具体，对于降低文章数理难度是有益的，而且由于有一个明确且直观的数值结果，也更便于理论成果转化运用。

“解说式模型”“玩偶模型”和“数值模拟”在“全模型”的基础上向“自然语言模型”靠拢，分别在严谨性、完整性和一般性三个维度上做出了让步，去掉了一个维度而保留两个维度，从而降低了数理难度。然而，这种让步仍然具有很大局限性，基本上是面向学术同行做出的让步，而没有真正地拉近“研、教、学、用”的距离。

具体来说，解说式模型和玩偶模型尽管有助于降低学术论文的数理难度，便于学术同行更快速地掌握论文中的核心思想、发现和结论，提高论文外审和得到认可的效率，但是这种简化仍然需要较高的前期知识储备和数理基础，并非面向初学者的，更多是面向大领域内的同行以及高年级博士研究生。数值模拟仍然建立在完整的模型基础上，使得模拟计算过程十分复杂，对数理统计、科学计算的要求很高，也很难直接应用。例如，对实务者来说，尽管有一个定量的数值结果，但是由于对数值模拟背后的理论机制不甚清楚，无法判断这个数值结果可信度如何，所以也不敢轻易采信数值结果作为决策依据。

二、数值示例的简化路径和开发流程

那么如何进一步地简化理论模型，从而真正面向初学者呢？我们必须再牺牲一个维度，只保留一个维度，那么应该保留哪一个维度呢？

（一） 数值示例的简化思路

在一些论述数学工具的论文特别是学术笔记中比较强调数学工具的“一般性”，例如，专门研究效用函数形式的论文或介绍不同效用函数形式的学术笔记，对应于图1中的F点。然而，如果模型中绝大部分过程都是数值四则运算和极为初步的微积分，那么学习难度就可以控制在中学阶段，面向的受众范围将大为提高。“一般性”是导致数学难度升级的主要原因，而且通常承载的理论思想较小，所以首先被排除的就是“一般性”。

在多数综述风格的专业文章中比较强调“完整性”。我国传统文科类论文和教学都基本采用这种风格，对应于图1中的G点。如图2中所示，这类文章会分两点分别来阐述变量a和变量e之间的关系：先讲述“a-b-c-e”这个主要传导机制，然后再讲述“a-b-d-e”这个次要关系。这种方式的优点在于面面俱到，能够让人们对“变量a和e之间的关系”有一个总体的结构性的认识。这类文章较少采用数学语言，而采用条分缕析的方式，也比较受实务者的欢迎，因此咨询报告也多采用这种方式。但是单纯强调“完整性”，而忽略了逻辑严谨性，将大大削弱这些研究的科学性，整个理论的传导机制不够清晰，许多逻辑环节上存在模糊、缺失和跳跃，更难以直接定量检验理论的成立性。

我们认为逻辑的“严谨性”是学术的灵魂，是新文科的重要特征，是最应当保留的部分。也就是说，我们可以利用玩偶模型，再采用数值的方式加以具体化，清晰地展示理论核心思想和逻辑传导路径。即便初学者也可以通过简单的计算，从假设前提出发，一步一步演算，最终得到理论的核心发现和结论。这就需要数值示例，即图1中的H点。

数值示例是将一个具有核心机制的玩偶模型进一步数值化，从而用直观的方式展现研究的核心机制、传导过程和主要结论。相对于数值模拟，它通过牺牲完整性实现模型的高度简化。相对于玩偶模型，它更为具体，通过牺牲一般性，仅依赖数值计算而非数学推导来展示核心思想，数学工具难度基本控制在高中数学范畴。数值示例选择了与“解说式模型”不同的简化思路：尽管牺牲了完整性和一般性，对于学生、公众以及实务者来说，仍然可以非常清晰地看到完整或主要的逻辑环节和顺序，把握学术成果的理论创新性和现实价值，而解说式模型则略过或模糊化部分逻辑环节，在一些情况下仍然容易给人以“似是而非”“似懂非懂”的感觉。

（二）数值示例的开发流程

数值示例的开发应当坚持以受众需求为导向的原则，我们提出了一个数值示例开发的标准化流程，包括以下几步：

步骤一是掌握“全模型”的基本原理、主要机制、核心结论和关键发现。开发数值示例的前提是开发者对“全模型”要非常了解，明白哪些是理论模型不可或缺的部分，哪些实际上是为了达到“完整性”和“一般性”而进行的拓展。

步骤二是对“全模型”尽可能简化，建立“玩偶模型”。这一步非常关键，有点类似于“叠叠乐”积木玩具（一款经典的木制益智积木玩具，玩家从堆叠起来的模型中轮流抽取小模块，抽取导致模型垮塌的一方判输），既要保持模型主体结构不会“垮塌”，又要小心翼翼地剔除模型中非必需的部分。建立“玩偶模型”的过程主要是将全模型中的一些次要内生机制关闭，将一些变量设为外生不变，同时采用更强的假设，将一些抽象的更一般的函数形式简化为具体的函数形式，例如，经济学中采用对数、平方根等更简单的效用函数，采用线性的生产函数等。但要注意的是，在这个过程中，要始终坚持对受众需求的分析，简化理论模型的最终目标永远是为了便于受众理解和把握理论核心机制。

步骤三是对“玩偶模型”进行赋值，使其从抽象的函数关系变为数值关系。赋值过程中有两点需要注意：一是赋值应当尽可能使得计算过程更为简单，例如数值取整数优于分数和小数；二是数值范围应当合理，并尽可能符合现实。虽然与数值模拟相比，数值示例中各参数取值并不要求特别精确，但与现实尽可能接近有助于加强数值示例的说服力，减少受众的困惑。

步骤四是根据赋值，计算出模型主要结果。在这个过程中，应当完整地展示计算的全过程，逐步计算出最终的结果。对计算结果进行分析，并根据需要探讨参数取值对模型结果的影响，从而让受众完全理解模型背后的逻辑和传导机制。

以上四个步骤中，第一步是前提，最关键的是第二步和第三步，这两步抽丝剥茧地去除了全模型的“一般性”和“完整性”，最后一步展示了数值示例的逻辑“严谨性”。上述流程较好地体现了数值示例的简化思路。

三、数值示例的开发案例

数学模型简化的问题虽然广泛存在于所有社会科学中，是新文科建设中面临的普遍问题，但由于社会保障学科所具有的综合性、交叉性、应用性特点，表现得尤为突出。如果社会保障学科能够很好地解决上述问题，推动数理模型以通俗易懂的方式走入本科生课堂，促进领域内不同学科背景学者的交流，对于其他社会科学都有极高的借鉴意义。下面以社会保障的财务运行模式为例，介绍如何建立数值示例。

（一） 样例背景

社会保障的财务运行模式主要分为两种：现收现付制，即当前发放给社会保障待遇领取者的资金主要直接向正在工作者征收的模式；积累制，即当前发放给社会保障待遇领取者的资金主要来自既往的基金积累。围绕这两个模式的优劣和社会福利效果，自1966年“艾隆条件”提出后，学者们进行了长达半个多世纪的研究和争论。Aaron提出在一定条件下，现收现付制可以实现资源的帕累托最优配置［9］。随后，经济学家在世代交叠模型中对这个理论进行非常深入而持久的研究，发现这个问题与政府债务［10］、资本黄金率［11］乃至房地产、金融泡沫等都有着很强的关联［12］，产生了极为丰硕的理论成果。

我们先运用“自然语言模型”来阐述这一理论：“世代是无穷的，现收现付制特点是用后一代人的资金去赡养前一代人，如果下一代人口增长速度很快，或者下一代人的收入增长速度很快，那么与其让上一代人存钱自我养老，不如直接将下一代人的收入转移给上一代人，可以使得至少有一代人利益改善，而没有任何一代人利益受损。”可见，自然语言虽然比较通俗，也能较好地向非专业人士传达一个理论的核心思想，但由于变量之间的逻辑关系不够清晰，受众处于“似懂非懂”的状态，对理论的认同和接受程度也会大打折扣。

下面我们看一下这个理论的“全模型”。首先需要建立一个世代交叠模型（Over lapping Generation Model，简称OLG），假设存在两代人，每代人效用函数最大化问题为：

maxctt，ctt+1U（ctt，ctt+1，ltt） （1）

s.t.ctt=wtltt-St-Tt，ctt+1=St（1+rt+1）+Pt+1

t时刻出生的代表性行为人将生活两期。第一期为年轻人，消费为ctt，取决于工资收入wtltt中除去储蓄预留以及社会保障缴费后剩余的部分。wt为工资率，而ltt为劳动时间。在进入第二期或者说在t+1时刻成了老年人，对应的消费为ctt+1，取决于储蓄连本带息的积累额st（1+rt+1）以及社会保障待遇Pt+1。

除代表性行为人决策之外，全模型还应当描述：企业基于利润最大化的决策，根据劳动力和资本的价格，即工资和利率，选择最优的劳动力雇佣水平以及使用的资本量；政府的预算平衡方程，即政府根据社会保障基金预算平衡的要求，确定缴费和待遇水平；市场达到一般均衡条件，即产品市场和资本市场的出清过程。而且，上述模型是一个动态结构，因此需要求解模型达到稳定状态的过程。模型甚至还可以考虑不确定性、经济增长等许多新的内生变量。

“全模型”的优点和缺点都是显而易见的，一方面它很好地体现了逻辑的“严谨性”、分析的“完整性”以及模型设定上的“一般性”。另一方面“全模型”过于复杂，逻辑链条过长，涉及的变量和机制过多，数理难度过高，不适合本科教学、初学者学习以及实务者把握应用。下面我们就分步骤论述如何构建这个理论对应的数值示例。

（二） 构建数值示例

1. 步骤一：全模型分析

首先我们需要对“全模型”进行分析，明确哪些是理论模型不可或缺的部分，哪些实际上是为了达到“完整性”和“一般性”而进行的拓展。在上述社会保障财务运行方式案例中，理论模型的核心机制是现收现付制可以通过代际赡养的方式，在一定条件下达成一个更优资源分配状态。因此，模型的动态结构、一般均衡效应、不确定性、增长性以及工资如何决定，市场如何出清，都不是理论中最重要、最核心的部分。在玩偶模型中，这些次要机制均可以剔除或关闭。

2. 步骤二：建立玩偶模型

如前所述，带有动态结构、不确定性和一般均衡效应的经济学模型通常都更为复杂，导致模型没有显式解，所以在本示例建立玩偶模型过程中，我们首先不考虑动态结构、不确定性和一般均衡效应。其次，本示例主要是分析劳动者的行为，因此也不需要考虑企业决策行为。再次，在劳动者行为决策问题中，劳动供给也不是必需的，只要保留劳动者在年轻和年老两期的消费情况即可。此外，可以将效用函数形式设为较为简单形式：

U（ctt，ctt+1，ltt）=ctt·（ctt+1）β （2）

公式（2）中的效用函数保留了基本的逻辑关系，人们的效用取决于年轻时期和年老时期的消费，β是折现率。接着，我们去掉模型的动态结构、一般均衡特征，假设一个“荒岛”禀赋经济［13］。年轻和年老的两代人生活在这个“荒岛”上，荒岛没有任何可耕种的土地，只种植着一些椰子树，定期会掉下椰子来，作为荒岛唯一的产品，椰子树即为“禀赋”。在t时刻出生的世代，年轻时期和年老时期的禀赋分别为ett和ett+1。暂时不要考虑荒岛容纳能力，假设荒岛上的居民以稳定的速度增长，每经过一个世代人口翻一倍。t-1时刻出生的人数为Nt-1，则t时刻的人口增长为Nt。在禀赋经济下，均衡意味着不浪费任何资源，个人消费永远等于每个人获得的禀赋，这也避免了个人效用最大化问题。

通过这个例子可以看出，建立“玩偶模型”的过程主要是将全模型中的一些次要机制关闭，将一些抽象的更一般的函数形式简化为具体的易操作的函数形式，以便获得显式解，但是保留模型最主要的思想。

3. 步骤三：赋值计算

上述的玩偶模型已经非常简单，可以非常方便地进行赋值运算。首先，假设公式（1）中的贴现率为0.5，而每一代人年轻时的禀赋为2，年老时的禀赋下降为1。每代人的效用值为：

U（ctt，ctt+1）=ctt·（ctt+1）β=ett·（ett+1）β=2·（1）0.5=2  （3）

这样的数值假设尽管简单，但是体现了人们收入随着年老而下降的风险，也产生了对社会养老保险的需求。其次，我们希望演示的是人口增长环境下现收现付制的优势，因此不妨如表1所示，假设t-1时刻人数Nt-1=100，到t时刻人口增长为200，此后依次递增。

下面，我们说明现收现付制在一定条件下可以增进社会福利。假设在每一个时刻，年轻人都从自己的禀赋中扣除1/3单位的禀赋，通过现收现付社会保障体系，禀赋交给了老年人。新的资源分配状态如表1中括号内的数字所示：初始的第0代人的禀赋为{ett，ett+1}={2，3/5}，后续世代的禀赋为{ett，ett+1}={3/5，3/5}。这样的转移支付是可行的，如在t+2时刻，每个年轻人转移1/3，合计转移1/3×400=400/3单位，每个老年人恰得到400/3/200=2/3。由于模型中每个老年人对应于两个年轻人，那么每个老年人可以得到2/3单位的禀赋。这时，初始的第0代人的效用为： U（c00，c01）=e0*0·（e0*1）β=2·（5/3）0.5=2.58

后续所有世代的效用为：

U（ctt，ctt+1）=et*t·（et*t+1）β=5/3.（5/3）0.5=2.15，t>0

由此得到了现收现付社会保障不存在和存在两种情形下的福利水平。

4. 步骤四：结果说明

对比引入现收现付社会保障体系前后的社会福利水平可以发现，通过社会保障体系，对初始的第0代人来说，增长的效用相当于提高了大约29%的禀赋（2.58/2-1）。对于后续世代来说，福利的增长也是巨大的。我们仅仅转移相当于年轻人禀赋16.67%（（1/3）/2=1/6）的资源，但是增长的效用却相当于原来每个年轻人的禀赋提高了7.58%（2.15/2-1），两者之比达到：

7.58%/16.67%=45.5%

相当于转移一单位财富就等于创造了0.455单位的财富。这体现了在人口增长时，现收现付增进社会福利的效果。

显然，相对于自然语言模型，数值示例能够更好地传达世代交叠模型在社会保障财务运行方面最重要的思想。相对于全模型，难度系数也大为降低，有助于学生建立对现收现付制运行特点的认识。事实上，这一禀赋模型还可以继续扩展：通过引入劳动者的最优储蓄行为的选择，可以完整演示艾隆条件，可以建立现收现付与国债之间等价性定理，可以演示现收现付制与最优资本存量之间的对应关系，甚至可以对中国养老金体系改革提供有益的参考。

四、总结与对策建议

自20世纪50年代开始，经济学、管理学等文科越来越多地借鉴理科中广泛使用的理论模型方法，这大大促进了文科的发展和科学化进程，但也导致文科前沿科研成果与普通大众、初学者和实务部门之间的距离不断拉大，这与文科关注人文社会的初衷并不相符。将前沿学术成果带入本科生课堂，传达给需要这些知识发现的实务工作者，正在变得越来越迫切。

学术研究中直接使用的“全模型”过于强调逻辑的“严谨性”、分析的“完整性”和变量关系的“一般性”，导致模型过于复杂，对专业和数学基础要求过高，而科普作品中的“自然语言模型”则容易让受众产生“似懂非懂”的感觉。“数值示例”在高度简化的“玩具模型”基础上，再进行具体的数值计算，既保留了理论模型最核心的机制，又能大大降低专业和数学基础的要求，更适合本科生、初学者和实务工作者。本文提出了一个构建数值示例的标准流程：第一步，掌握“全模型”的基本原理、主要机制、核心结论和关键发现；第二步对“全模型”尽可能简化，建立“玩偶模型”；第三步对“玩偶模型”进行赋值，将变量间抽象的函数关系变为数值关系；第四步，数值计算出主要结果，并对结果进行分析说明。

科学知识的传播通常不是“一站式”的，特别是学术前沿理论模型，往往需要“多级传递”：先从学术前沿到学术同行和博士生，再到本科生和初学者，最终面向大众。在这三个环节中，第一个环节随着我国文科学术体系的发展已经建立了成熟的传播系统。在第三个环节上，近年来随着科普创作生态环境的改善和自媒体的发展，越来越多的科技工作者开始从事科普创作和宣传。数值示例开发有助于弥补第二个环节的不足。本文接下来探讨在新文科建设中完善数值示例开发体系的对策建议。

（一） 培养高素质的数值示例开发人才

数值示例开发对人才素质的要求较高。数值示例开发者首先要对“全模型”有着不亚于原创者的非常深刻的理解，才能很好地将全模型拆解开，保留理论模型核心机制的同时剔除或关闭扩展衍生的部分。在这个过程中，数值示例开发者需要充分运用各种简化技巧，这就要求开发者非常清楚理论模型每个“元器件”扮演的角色，发挥的功能，方能删繁就简。最后，数值示例开发者还需要对受众有充分的分析，掌握丰富的教学经验和技巧，从而能够根据受众需求进行案例设计，有效地向受众传达理论模型的核心思想。

显然，非专业性的科普工作者很难满足上述三个条件，数值示例开发主要依赖在科研一线的高校文科教师。所以，应当向高校文科教师广泛地推广数值示例教学法，鼓励教师自主设计、共同开发和分享优秀的数值示例，逐步带动教师在完成前沿科研论文的过程中同步开发数值示例，进一步扩大个人学术成果的传播和运用范围。

（二） 建立数值示例传播共享平台

在经济学、管理学教学实践中，部分教师会自主设计数值示例，降低理论模型难度，便于学生理解。但是，这些数值示例散落在各个课程中，无法相互分享和组织共同开发，质量也参差不齐。反过来，由于开发的数值示例缺乏传播展示的平台，不能转化为个人标志性的成果，也导致高校教师从事数值示例开发的热情不足。

建议逐步建立三类数值示例的传播共享平台，简称为“一库、一刊、一赛”：一是仿照“MBA案例库”“MPA案例库”等，建设各个学科的“数值示例库”，选择性收录各类优秀的数值示例，入库的示例对外开放，供教师、同学和实务工作者使用；二是设立“数值示例”专门期刊，发表基于文科前沿研究成果的优秀数值示例；三是设立“数值示例比赛”，鼓励学者和在校学生参与数值示例的开发，对优秀案例给予资助鼓励。

（三） 规范和保护数值示例的产权

数值示例开发在著作权中应当被视为一种“改编权”。我国《著作权法》规定“改编权，即改变作品，创作出具有独创性的新作品的权利”，具体可视为将“全模型”改编为“简本”。《著作权法》第二节第三条规定，“改编、翻译、注释、整理已有作品而产生的作品，其著作权由改编、翻译、注释、整理人享有，但行使著作权时不得侵犯原作品的著作权”。另第十二条规定，“使用改编、翻译、注释、整理、汇编已有作品而产生的作品进行出版、演出和制作录音录像制品，应当取得该作品的著作权人和原作品的著作权人许可，并支付报酬”。同时，在《著作权法》第四节第二十四条中也规定了不需要支付报酬的情形：“为学校课堂教学或者科学研究，翻译、改编、汇编、播放或者少量复制已经发表的作品，供教学或者科研人员使用，但不得出版发行。”这表明正式出版数值示例仍然需要得到原作者许可并支付报酬，但完全可以用于课堂教学。建议规范和保护数值示例产权可以从以下三个方面着手：一是数值示例应视为改编的新著作，尊重改编者的著作权，对侵权行为应予打击；二是公开出版数值示例应当取得原作者的许可，支付相应报酬，这样可以鼓励全模型原作者自主开发数值示例，或者原作者与改编者合作共同开发；三是明确课堂教学和科研人员使用不受著作权限制，这样可以扩大数值示例的传播范围。

【参考文献】

［1］洪永淼.“新文科”和经济学科建设［J］.新文科教育研究，2021，1（01）：63-81+142.

［2］朱富强.经济学数理化倾向及其原因探析［J］.学习与探索，2009（03）：122-127.

［3］杨子砚.“数理经济学”课程的教学改革与实践［J］.经济资料译丛，2021（03）：97-104.

［4］朱富强.经济现象的复杂性与经济学数量化的认识论局限［J］.财经科学，2009（08）：49-55.

［5］朱富强.“数量拜物教”引致的经济学形式化庸俗化［J］.改革，2016（01）：130-140.

［6］张晖明，邓霆，翁恺宁.人文精神的回归与马克思主义经济学的理论创新［J］.政治经济学评论，2012，3（04）：18-32.

［7］洪永淼，汪寿阳.数学、模型与经济思想［J］.管理世界，2020，36（10）：15-27.

［8］Epstein， L. and S. Zin. Substitution， Risk Aversion， and the Temporal Behavior of Consumption and Asset Return： A Theoretical Framework［J］.Econometrica，1989，57（04）：937-968.

［9］Aaron， Henry J. The Social Insurance Paradox［J］.The Canadian Journal of Economics and Political Science， 1966，32（03）：371-374.

［10］Diamond， Peter. National Debt in a Neoclassical Growth Model［J］.American Economic Review， 1965，55（05）：1126-1150.

［11］Samuelson， Paul A. Optimum Social Security in a Life-Cycle Growth Model［J］.International Economic Review， 1975，16（03）：539-544.

［12］ McCandless G. and N. Wallace. Introduction to Dynamic Macroeconomic Theory： An Overlapping Generations Approach［M］. Massachusetts：Harvard University Press，1992.

［13］Samuelson， Paul A. An Exact Consumption-Loan Model of Interest With or Without the Social Contrivance of Money［J］.Journal of Political Economy， 1958，66（06）：467-482.

The Simplification of Mathematical Models in the Construction of New Liberal Arts

Qin Wenjia，Zhang Yi

Abstract： At present， many fields of liberal arts are increasingly inclined to carry out frontier research with quantitative mathematical models in research methods. However， liberal arts learners and practitioners have relatively weak foundations in using mathematical tools， resulting in a serious disconnect between research and teaching， learning and application. Through a framework of thinking on the simplified path of mathematical models， this paper finds that compared with natural language models， full models， illustrative models， toy models and numerical simulations， numerical examples can greatly reduce the threshold of mathematical tools of liberal arts， while maintaining the logic， main ideas and discoveries of scientific research， thus greatly narrowing the gap between "research and teaching， learning and application". This paper proposes a standard process for the development of numerical examples， and provides a sample. We argue that promoting the development of numerical examples requires the participation of high-quality professional scholars on the one hand， and the corresponding academic environment and resources on the other hand.

Key words： new liberal arts; numerical examples; theoretical models; mathematical tools

（责任编辑 肖地生）