基于多项式响应面MDOE的低速风洞试验方法研究

摘 要：现有的基于各类统计模型的现代试验设计（MDOE）方法存在计算量大、建模较复杂导致整体风洞试验效率下降的不足。针对这一问题，本文提出一种将多项式响应面模型与现代试验设计相结合的优化设计方法。采用中心复合设计在自变量区间中划分试验点并进行风洞试验获取气动力，利用最小二乘法确定多项式待定系数，构建响应面模型，并进行方差分析及显著性检验，最后选取了5个传统单变量（OFAT）方法试验点检验响应面模型的拟合精度。结果表明，与传统单变量风洞试验方法相比，本文提出的基于多项式响应面MDOE的低速风洞试验方法具有建模容易、计算量较小、预测校准的优点，可使试验样本点减少50%左右，能够有效提升风洞试验效率。

关键词：多项式响应面模型； MDOE； 风洞试验； 中心复合设计； 方差分析

中图分类号：V211.52 文献标识码：A DOI：10.19452/j.issn1007-5453.2024.06.014

一直以来，风洞试验研究都是探索飞行器气动机理、验证气动理论和优化气动设计采用的主要手段之一[1]。目前，风洞试验普遍采用的试验方法是调整风洞流场各参数到预定值，然后在只改变模型的一个变量（如俯仰角），同时锁定试验模型其余姿态变量的条件下，获取随该变量变化的模型气动性能，这就是传统的单变量（OFAT）方法。OFAT方法是一种基于数据、以数据为中心的方法，需要进行的风洞试验次数较多而导致试验成本高效率低[2]。

1997年，美国国家航空航天局（NASA）兰利研究中心Deloach[3]首次将现代试验设计（MDOE）方法应用到风洞试验领域，减少了试验样本点和吹风时间。MDOE方法与一次只改变一个自变量的OFAT方法不同，MDOE方法一次要改变两个或两个以上的自变量，通过合理划分试验点，达到缩短试验周期的目的[4]。

国外Underwood[5]在NASA兰利研究中心对跨声速风洞进行了基于方差分析模型的MDOE方法壁压校准研究，提高了试验效率和校准精度。Rhode[6]利用基于稳健回归模型的MDOE方法和OFAT方法分别对风洞进行校准，前者有效拓宽了风洞运行包线内的校准范围并降低了校准周期和成本。Deloach[7]在NASA兰利研究中心统一规划风洞采用基于克里金模型的MDOE方法改进导弹类模型风洞试验质量和生产率问题，与OFAT方法相比，MDOE方法在确保数据精度的情况下，缩短了试验周期。Landman[8]利用MDOE方法结合径向基模型，开展了天平校准研究，结果表明，MDOE方法校准所需的加载量较OFAT方法大幅减少，MDOE方法校准点和验证点准度较好。国内唐志共等[9]提出了基于三角级数模型的MDOE方法，并开展了风洞试验，结果表明，该方法能满足模型预测精度，减少试验样本点。张江等[10]针对飞行器气动规律存在多变量耦合的情况，提出了基于非参数模型的MDOE方法，研究表明，该方法所需的试验点要少于OFAT方法的试验点，且构建的模型能较为准确地反应飞行器气动规律。MDOE方法基于试验数据建立统计模型来获取飞行器气动规律，现有的基于各类统计模型的MDOE风洞试验方法[11-17]，尽管能有效减少试验样本点数量，但由于统计模型表达式复杂，求解较为困难，从而导致整体风洞试验效率并未明显提高。

因此，本文进行了基于多项式响应面MDOE的低速风洞试验方法研究，通过中心复合设计方法选取少量试验点，建立二阶多项式响应面模型。同时，加入OFAT方法试验点验证模型的拟合精度。结果表明，与传统单变量方法相比，基于多项式响应面MDOE的风洞试验方法，能减少试验样本点和模型拟合时间，有效地提升风洞试验效率。

1 多项式响应面MDOE方法

1.1 多项式响应面模型

1.2 MDOE方法

1.2.1 区间分层

试验以某飞行器机身作为试验对象，选取以下典型状态及控制参数范围：试验风速为16m/s，试验俯仰角α=-20°～ 20°，偏航角β=0°～20°，根据OFAT方法划分出试验样本点，如图1所示，其中红点为试验状态。

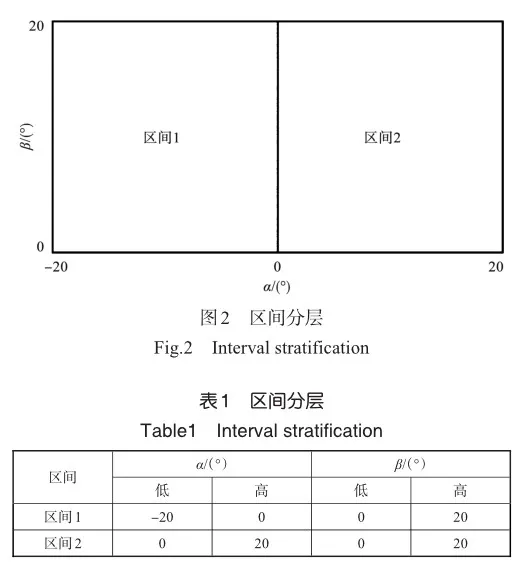
为了避免多项式响应面模型中增加高阶项，引入区间分层技术，将俯仰角区间划分为两层，如图2、表1所示。

1.2.2 试验点数量

式中，p为多项式项数；d为多项式阶次；k为多项式元数。

由于飞行器气动规律一般为非线性，为了获得较为准确的响应面，采用二阶多项式响应面模型来逼近。本文用二元二次多项式响应面模型对两个区间进行建模，即k=2，d=2，最小试验点数量代入式（2）得p=6。由于多项式响应面模型中存在对模型精度影响较大的点，这些点会引起“杠杆效应”，放大整个多项式响应面模型的误差，因此需要增加部分点改善杠杆效应。为保证响应面预测值在平均95%置信概率水平下与自变量空间中任一点的真实结果不出现显著差异，试验点数量N需要满足[4]

在本文设计的试验中，一个二维数据空间需达到10个（N=1.625×6=9.75）就可以使预测值落在95%置信区间内。

得出自变量空间试验样本点数量，需要进行试验设计确定试验点取值，使多项式响应面有较好的拟合精度。

1.2.3 试验点分布

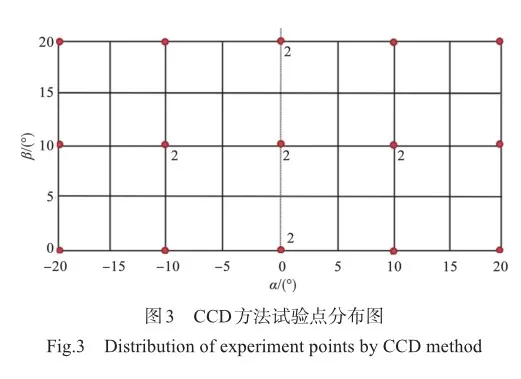
中心复合设计由Box和Wilson于1951年提出，中心复合设计（CCD）方法能够估计线性以及二阶交互项的效应，是一种高效的试验设计方法[19]。本次试验采用CCD对经过区间分层后的设计空间进行划分，由于区间一和区间二均有10个试验样本点，所以依据设计中心能抑制预测方差，将在中心处进行两次试验。图3共有15个点，其中5个点重复了两次，点旁边的数字表示重复次数，因此总共20个试验点。

2 试验设备

（1） 风洞

本次试验在中国直升机设计研究所气动试验台进行，试验台是一座8m×6m开口直流式低速风洞。试验段风速范围为5～50m/s，局部气流偏角△α≤ 0.5°，△β≤ 0.5°，湍流度ε≤ 0.5°。

（2） 模型

本次试验风速为16m/s，俯仰角α=-20°～20°，偏航角β= 0°～20°，试验对象为某飞行器机身模型，模型试验在低速风洞中进行，为后续模型样机研制提供技术支持，同时为计算流体力学（CFD）及飞行动力学分析提供技术参考。

（3） 数据采集

依据选取的试验样本点，采集各试验状态下模型作用在天平上的气动力（阻力、升力和侧向力），数据采集设备使用六分量盒式天平测量模型气动力，试验风速稳定后，控制模型俯仰角和偏航角到达试验点状态，采集天平信号，每个状态下保证获取10s稳态数据。

3 多项式响应面建模及分析

3.1 多项式响应面模型构建

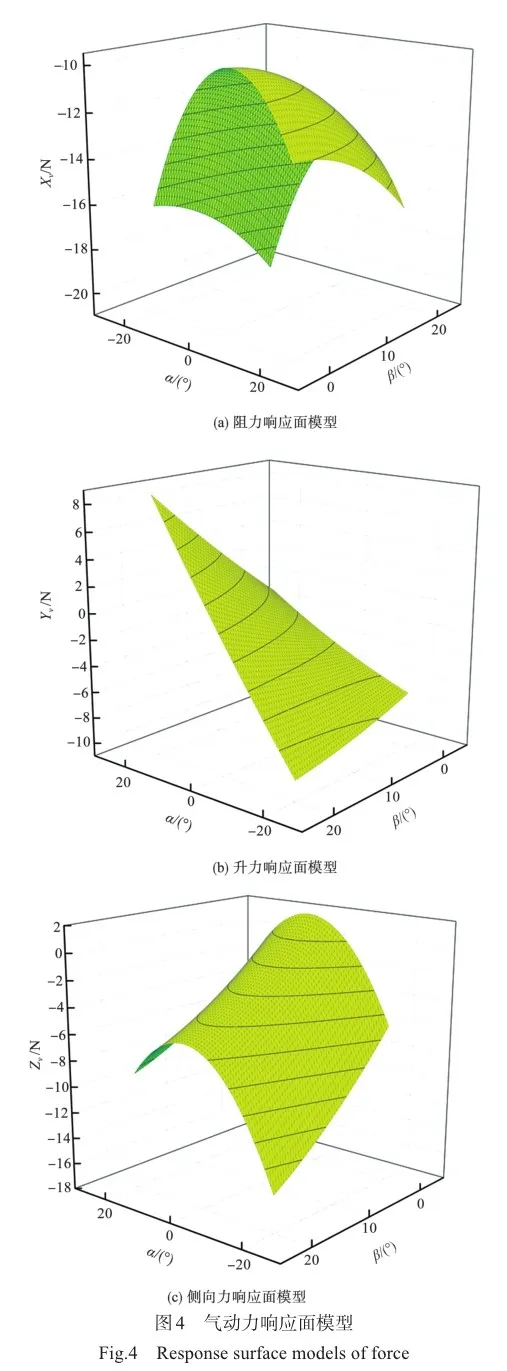
多项式响应面模型在区间交接处（俯仰角为0°）时的拟合误差存在部分差异，为确保响应面模型的连续性，只能选用一区间或二区间中的一个模型。由于一区间的拟合误差相较于二区间更小，因而将0°俯仰角归入一区间，升力、阻力和侧向力的最终响应面模型如图4所示。

3.2 方差分析及显著性检验

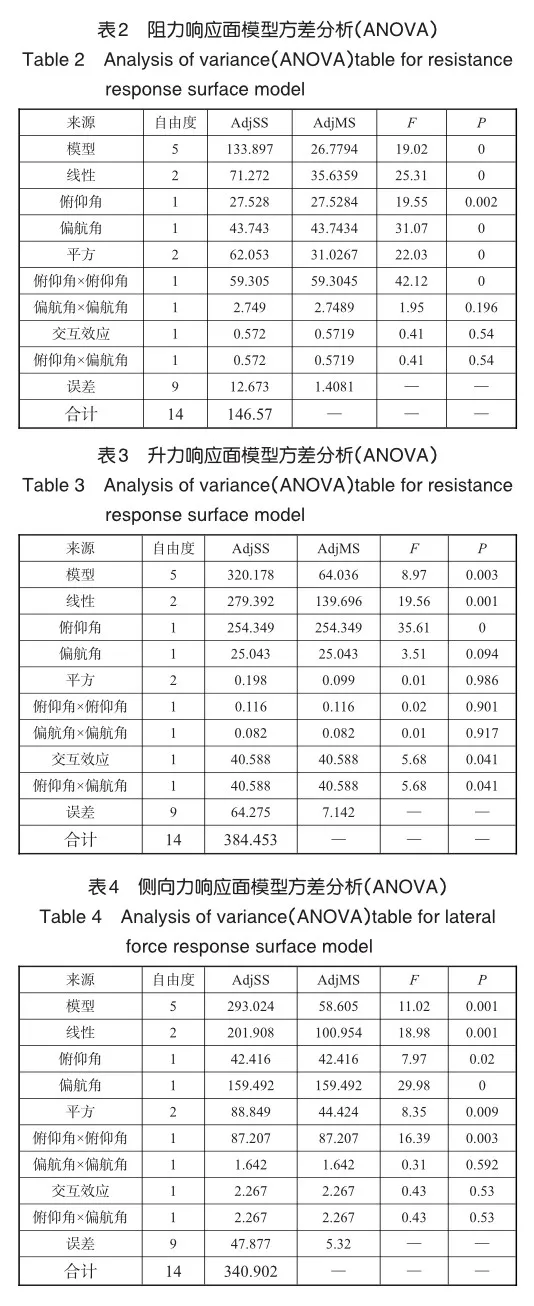
基于多项式响应面MDOE方法建立响应面模型后，采取方差分析及显著性检验，验证响应面模型的可靠性以及各变量之间的显著程度[16]。在置信度为0.05的情况下，得到机身气动力响应面模型的方差分析表，见表2～表4（AdjSS、AdjMS、F、P分别为调整平方和、离差平方和、检验统计量和显著性水平）。

各气动力响应面模型的P值均小于0.05，所以模型为“高度显著”，验证了模型的可靠性。同时，观察各项效应的显著性，可以看出俯仰角在升力响应面模型中高度显著（P<0.05），偏航角、偏航角×偏航角在侧向力响应面模型中高度显著，俯仰角、偏航角、俯仰角×俯仰角在阻力响应面模型中高度显著。

3.3 模型验证

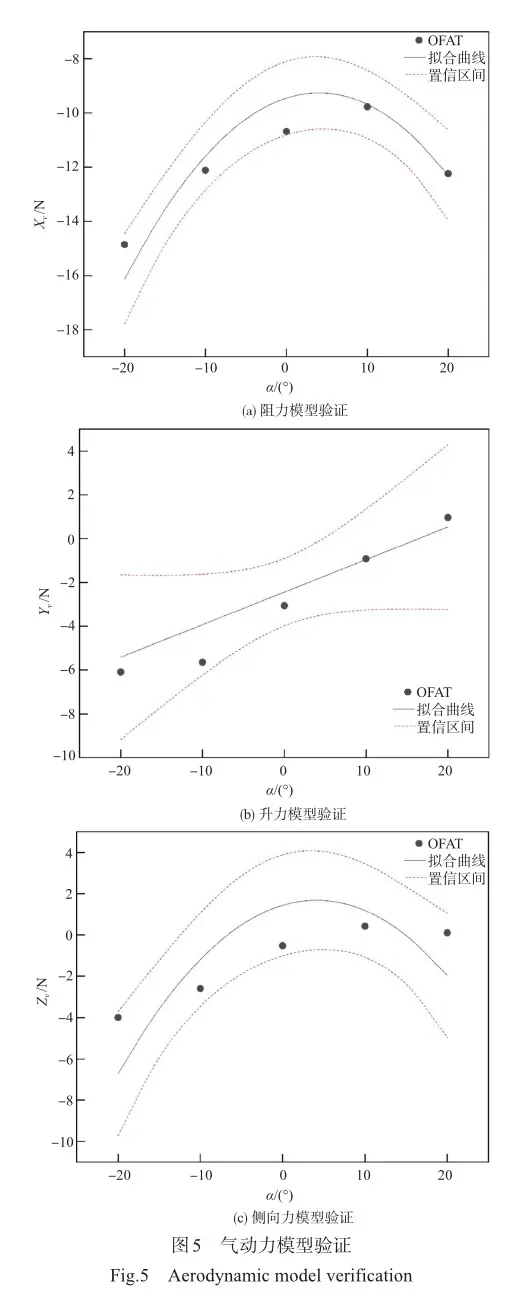
在β=0°的多项式响应面模型上选取5个OFAT方法试验点检验其是否能够落在拟合曲线的95%置信区间内，验证多项式响应面模型的有效性，检验结果如图5所示，其中红色曲线代表上下置信区间，蓝色曲线代表本试验拟合曲线，黑点代表OFAT方法检验点。

从图5中看出，基本所有的点都能落入95%置信区间内，说明基于多项式响应面MDOE方法构建的响应面模型精度足够。

4 结论

本文提出一种基于多项式响应面MDOE的低速风洞试验方法，通过中心复合设计划分少量试验样本点，建立具有较高精度的二次多项式响应面模型，验证了多项式响应面MDOE方法在风洞试验领域的可行性，并得出了以下结论：

（1） 与传统单变量方法相比，通过多项式响应面MDOE方法对风洞机身试验进行优化设计，具有建模容易、计算量较小、预测较准的优点，使风洞试验样本点减少了50%，显著提高了试验效率。

（2） 风洞试验结果通过多项式响应面模型表示，能任意获得自变量空间内试验样本点响应值，通过以点带面，可插值得到更多的数据。

（3） 方差分析及显著性检验结果表明，基于多项式响应面MDOE方法构建的模型，能有效反应出俯仰角和偏航角对飞行器基本气动特性的影响规律。

参考文献

[1]黄明其，袁红刚，武杰.直升机旋翼气动特性风洞试验技术[M].北京：国防工业出版社，2022. Huang Mingqi， Yuan Honggang， Wu Jie. Wind tunnel test technique of helicopter rotor aerodynamic characteristics[M]. Beijing： National Defense Industry Press， 2022.（in Chinese）

[2]战培国. MDOE风洞试验方法研究[J].航空科学技术， 2011，22（6）：11-14. Zhan Peiguo. Review of modern design of experiment methods in wind tunnel test[J]. Aeronautical Science & Technology， 2011， 22（6）：11-14.（in Chinese）

[3]Deloach R. Applications of modern experiment design to wind tunnel testing at NASA Langley Research Center[J]. AIAA Journal， 1998， 7（13）： 55-64.

[4]张江，秦永明，马汉东.亚跨超风洞现代试验设计方法研究[J]. 空气动力学学报，2015，33（3）：384-391. Zhang Jiang， Qin Yongming， Ma Handong. Applications of modern design of experiments to wind tunnel test[J]. Acta Aerodynamic Sinica， 2015， 33（3）： 384-391.（in Chinese）

[5]Underwood P J. National transonic facility wall pressure calibration using modern design of experiments[C]. AIAA Aerospace Science Meeting and Exhibit， 2001.

[6]Rhode M N. Hypersonic wind tunnel calibration using the modern design of experiments[C]. AIAA Aerospace Science Meeting and Exhibit， 2005.

[7]Deloach R. Comparison of resource requirements for a wind tunnel test designed with conventional vs. modern design of experiments methods[C]. AIAA Aerospace Science Meeting and Exhibit， 2011.

[8]Landman D. A wind tunnel external balance calibration using design of experiments[C]. AIAA Aerospace Science Meeting and Exhibit， 2007.

[9]唐志共，王文正，陈功.气动模型在现代气动试验设计中的应用研究[J].空气动力学学报，2017，35（2）：172-176. Tang Zhigong， Wang Wenzheng， Chen Gong. Research on the application of aerodynamic models in modern design of aerodynamic experiments[J]. Acta Aerodynamic Sinica， 2017， 35（2）： 172-176. （in Chinese）

[10]张江，秦永明，马汉东.风洞MDOE的形式实验设计方法研究 [J].空气动力学学报，2016，34（1）：59-69. Zhang Jiang， Qin Yongming， Ma Handong. Formal design of experiments method of mdoe in wind tunnel tests[J]. Acta Aerodynamic Sinica， 2016， 34（1）： 59-69. （in Chinese）

[11]于晟浩， 袁吉森， 高亮杰， 等. 三维超声速后掠翼转捩的eN-神经网络模型预测[J].力学学报，2023，55（6）：1236-1246. Yu Shenghao， Yuan Jisen， Gao Liangjie， et al. eN -neural network model for predicting transition of 3D supersonic swept wing[J]. Chinese Journal of Theoretical and Applied Mechanics， 2023， 55（6）： 1236-1246.（in Chinese）

[12]马昕晨，陈志辉，赵雅周. 基于响应面法的轴向混合励磁双凸极航空发电机优化设计[J].航空科学技术，2022，33（10）：74-81. Ma Xinchen， Chen Zhihui， Zhao Yazhou. optimization design of axial hybrid excitation doubly salient aerospace machine based on response surface method[J]. Aeronautical Science & Technology， 2022， 33（10）：74-81.（in Chinese）

[13]许瑞飞，段卓毅，钱瑞战.基于Kriging代理模型的高升力构型优化设计[J].航空科学技术，2023，34（3）：58-63. Xu Ruifei， Duan Zhuoyi， Qian Ruizhan. Optimization design of high-lift configuration using Kriging model[J]. Aeronautical Science & Technology， 2023，34（3）：58-63.（in Chinese）

[14]鲍诺，王春洁，赵军鹏. 基于响应面法的结构动力学模型修正 [J]. 振动与冲击，2013， 32（16）：54-58. Bao Nuo， Wang Chunjie， Zhao Junpeng. Modification of structural dynamics model based on response surface method[J]. Journal of Vibration Shock， 2013， 32（16）： 54-58. （in Chinese）

[15]李永华，魏武松，张旭. 基于多项式响应面代理模型的齿轮修形量优化 [J]. 机械传动，2020，44（11）： 27-34. Li Yonghua， Wei Wusong， Zhang Xu. Polynomial-based optimization of gear modification for response surface proxy model[J]. Mechanical Drive， 2020，44（11）： 27-34. （in Chinese）

[16]孙喜龙，王登峰，荣宝军. 响应面法在汽车侧面结构多目标优化中的应用 [J]. 机械科学与技术，2022， 41（7）：1039-1047. Sun Xilong， Wang Dengfeng， Rong Baojun. Application of response surface method in multi-objective optimization of vehicle side structure[J]. Mechanical Science and Technology for Aerospace Engineering， 2022，41（7）：1039-1047.（in Chinese）

[17]成棣，王成国，刘金朝.两种响应面方法在车轮踏面优化中的应用分析比较[J]. 中国铁道科学，2010，31（3）：64-69. Cheng Di， Wang Chengguo， Liu Jinchao. Application analysis and comparison of two response surface methods in wheel tread optimization[J]. China Railway Science， 2010， 31（3）：64-69. （in Chinese）

[18]尤文佳，王慧杰，韩仁坤，等.高超声速风洞现代试验设计方法研究[J].实验流体力学，2022，36（3）：20-32. You Wenjia， Wang Huijie， Han Renkun， et al. Using modern design of experiments method for hypersonic wind tunnel test[J].Journal of experiments in Fluid Mechanics， 2022， 36（3）： 20-32. （in Chinese）

[19]李多，曹军义，张征宇.跨声速风洞现代试验设计方法应用研究[J].空气动力学学报，2018，36（1）：26-30. Li Duo， Cao Junyi， Zhang Zhengyu. Applications of modern design of experiment method in transonic wind tunnel[J]. Acta Aerodynamic Sinica， 2018， 36（1）：26-30. （in Chinese）

Research on Low Speed Wind Tunnel Test Method Based on MDOE of Polynomial Response Surface

Jiang Jiawei， Cheng Qiyou， Liu Zhengjiang， Chen Weixing

National Key Laboratory of Helicopter Aeromechanics， China Helicopter Research and Development Institute，Jingdezhen 333001， China

Abstract： The existing modern design of experiment （MDOE） methods based on various statistical models have a large amount of calculation and complex modeling， which leads to a decrease in the efficiency of the overall wind tunnel test. In order to solve this problem， an optimization design method combining polynomial response surface model with modern design of experiment is proposed in this paper. The central composite design was used to divide the test points in the independent variable interval and the wind tunnel test was carried out to obtain the aerodynamic force. The polynomial undetermined coefficients were determined by the least square method， and the response surface model was constructed. The analysis of variance and significance test were carried out. Finally， five traditional single variable （OFAT） method test points were selected to test the fitting accuracy of the response surface model. The results show that compared with the traditional univariate wind tunnel test method， the low-speed wind tunnel test method based on polynomial response surface MDOE proposed in this paper has the advantages of easy modeling， small calculation amount and prediction calibration， which can reduce the test sample points by about 50% and effectively improve the efficiency of wind tunnel test.

Key Words： polynomial response surface model； MDOE； wind tunnel test； central composite design； analysis of variance