一维立方非线性刚度周期结构色散特性研究

摘 要：研究立方非线性刚度单胞阵列形成一维周期结构后的色散特性，对飞机壁板振动控制的研究具有一定的促进作用。首先构建一维线性刚度周期结构的动力学模型，基于布洛赫理论（Bloch theorem）推导了其色散方程，并对其色散特性和弹性波传播现象进行分析。进而建立含立方非线性刚度单胞的一维周期结构的动力学模型，利用摄动法推导该周期结构的色散方程，分析非线性刚度的软、硬和激励振幅对其色散特性以及弹性波传播产生的影响。最后考虑到飞行器壁板复杂工作环境，避免摄动法仅适用于弱非线性的局限性，给出含立方非线性刚度一维周期结构色散关系的谐波平衡法的求解过程，对比两种方法的求解结果。本文为利用非线性周期结构对飞行器壁板进行振动控制的进一步研究奠定基础，对非线性声子晶体低频减振研究也具有一定的促进作用。

关键词：周期结构； 色散特性； 摄动法； 谐波平衡法； 非线性

中图分类号：V223 文献标识码：A DOI：10.19452/j.issn1007-5453.2024.06.008

基金项目： 航空科学基金（20161553016）；广东省基础与应用基础研究基金（2022A1515011497）；西安交通大学复杂服役环境重大装备结构强度与寿命全国重点实验室开放课题基金（SV2023-KF-19）

壁板是飞行器中常见的一种结构形式，在航空航天领域具有广泛的应用[1-3]。在外激励或气动力作用下，壁板结构会产生振动，带来诸多危害[4]。一方面，飞行器壁板结构振动会影响仪器仪表的正常工作，甚至产生疲劳问题，损坏壁板结构或减少其使用寿命；另一方面，飞行器壁板振动所辐射的噪声还会增大舱内的噪声量级，影响乘员舒适度。因此，如何有效地控制壁板结构的振动是现代飞行器发展亟须解决的关键问题之一。

经过近百年的研究，研究人员已经提出了多种对振动控制的被动和主动的方法[5]。传统的动力吸振器通常采用线性刚度设计，只有很窄的吸振频带宽度，为了克服这一缺点，Gendelman[6]提出了一种立方非线性刚度振子结构，该结构具有质量小、吸振频带宽、吸振效率高、能量传递速度快及靶向能量传递等优点，这样的非线性振子称为非线性能量阱（NES）。在结构中，振动通常以弹性波的形式传播[7]，对结构或材料中的弹性波行为进行调控是实现振动控制的一种有效手段，从20世纪50—60年代起，研究人员就对周期结构中的波传播理论展开研究，试图利用周期结构作为减振单元用于振动控制[8]。具有周期性特征的结构广泛存在于航空航天、机械和土木工程中，如飞机中的加筋板[9-11]、涡轮叶片[12]、抗冲击泡沫[13]、多层建筑和多跨桥梁[14-16]等。周期结构具有特殊的色散关系，只有频率处于特定的“传播区”，谐波才可以无损耗地传播，否则即使在没有阻尼的情况下，谐波也会因为布拉格散射或局域共振衰减。如果将这种立方非线性刚度单元阵列形成周期结构（简称立方非线性刚度周期结构），将同时具有非线性和周期特性，进而可以利用非线性单元的带宽特点和周期结构的色散特性实现更加优良的振动控制性能，然而鲜有将关于立方非线性刚度周期结构应用于壁板结构振动控制的研究。

对于周期结构的研究核心在于对结构中的波传播特性进行研究，为求解方便，大多将其等效为弹簧质量链进行研究[17-18]。对于一维线性刚度周期结构，高明等[19]针对三振子周期单元，通过引入奇异性理论分析了其色散曲线的拓扑结构，进而确定了带隙范围。武恒星等[20]给出了含双质量谐振单元的声学超材料杆中弹性波传播色散关系的解析解，发现通过引入双质量谐振单元，进而在谐振单元中引入阻尼，可以产生较宽的带隙。尽管线性刚度周期结构表现出许多有趣的波传播特性，但也存在很多限制，如某些情况下小位移假设不适用等[21]。非线性周期性结构具有丰富的波传播特性，有望突破低频宽带振动的限制。位琳帅[22]研究了双质量颗粒链的色散特性，并在颗粒链中引入了缺陷，发现此时波的传播会表现出类似于二极管的特性。Narisetti等[23]基于摄动法，研究了具有立方非线性刚度的不同周期结构的色散特性。尽管关于非线性周期结构有一定研究，但立方非线性方程求解一般比较困难，非线性刚度周期结构中波传播的研究主要集中于颗粒周期结构的3/2次幂非线性刚度，关于立方非线性刚度周期结构中的波传播问题研究较少。

现有关于立方非线性刚度周期结构的研究主要关注弱非线性，因此其求解都采用Narisetti等[23]提出的摄动法。摄动法仅适用于弱非线性，谐波平衡法既适用于弱非线性，又适用于强非线性，使用时不需要考虑非线性强度的问题[24]。但是关于非线性强度的强、弱只是相对的，没有明确定义，因此摄动法的适用环境并不明确。对此，本文基于立方非线性刚度周期结构，系统分析了一维线性刚度周期结构和一维立方非线性刚度周期结构的色散特性，给出了谐波平衡法求解立方非线性刚度周期结构的过程，对比分析了摄动法和谐波平衡法的求解结果。本文通过研究立方非线性刚度周期结构的色散特性，将非线性和周期结构的优点有效结合起来，同时，通过谐波平衡法无须考虑周期结构非线性强度的特性，避免了摄动法的适用环境问题，具有普适性，为基于非线性振子周期结构的飞行器壁板振动控制的进一步研究奠定了前期基础。

1 一维立方非线性刚度周期结构模型

磁力因其特有的非线性特性，被广泛应用于NES的构建[25]，本文利用稀土钕铁硼圆形带孔磁铁实现立方非线性刚度。考虑图1（a）所示的单胞结构，其中相邻磁铁间表现为互斥作用，悬浮磁铁在两个固定磁铁之间移动。在忽略重力的情况下，固定磁铁与悬浮磁铁之间的磁力是相互对称的，所以建立如图1（b）所示的试验模型，以固定磁铁中间位置为位移零点，通过改变砝码重量改变悬浮磁铁的位置，拟合得出力—位移曲线如图1（c）所示。根据已有研究[26]，力—位移曲线的拟合结果可以表达为k1x+k3x3的多项式形式，其中k1表征线性刚度，k3表征立方非线性刚度。当k3>0时为硬非线性刚度，当k3<0时为软非线性刚度[27]。通过拟合结果可见单胞结构表现为典型的立方非线性刚度形式。

利用该非线性刚度单胞结构，将其阵列形成周期结构，如图2所示。当周期结构受到小振幅激励时，悬浮磁铁在平衡位置附近振动，刚度表现为线性；当周期结构受到的激励振幅较大时，悬浮磁铁偏离零点位置较远，刚度表现为立方非线性特性。考虑周期结构的波传播特性，研究该单胞阵列形成的立方非线性刚度周期结构的色散特性，有益于下一步利用该周期结构对振动控制的研究。

2 一维线性刚度周期结构波传播特性分析

当受到小振幅激励时，可将阵列形成的周期结构等效为一维线性单原子弹簧质量链（简称线性单原子链），如图3所示，图中虚线框所示为一个单胞。

单胞由单个弹簧和集中质量串联而成，图4为图3所对应模型的布里渊区及不可约布里渊区，因为色散关系具有对称性，通常一维模型只需考虑布里渊区的一半，即不可约布里渊区，就可以描述模型的色散特性。

根据式（7）可以看出，对于线性单原子链，其色散与单胞的固有频率和外激励频率有关，与其他因素无关。线性单原子链色散曲线如图5所示，其中ql在图中用μ来表示。可见当Ω<2时，即当激励频率低于单胞固有频率两倍时，弹性波在该线性刚度周期结构中传播呈现通带，可以无损耗地传播。当Ω>2时，没有对应的实数波解，即为禁带，此时波的衰减可以用给定频率下通过式（7）求得的波数的虚部来表征。当Ω=2时的频率，即两倍固有频率，可以称作线性单原子链波传播的截止频率。

根据式（7），绘出μ的实部（传播常数）和虚部（衰减常数）随Ω变化的曲线，分别如图6和图7所示。图6为波数的实部，在Ω≤2时，其与图5中的色散曲线相对应，当Ω>2时，其为恒定值π；图7为波数的虚部，在Ω≤2时等于零，在Ω>2时随着Ω的增大而增大，这表明通过单原子弹簧质量链传播的波的空间衰减率也随着激励频率的增大而增大。

3 一维立方非线性刚度周期结构波传播特性分析

3.1 摄动法

当受到激励振幅较大时，根据图1（c）的力—位移曲线可知，单胞表现为立方非线性形式，此时可以将单胞阵列形成的周期结构等效为如图8所示的一维非线性单原子弹簧质量链（以下简称非线性单原子链）。

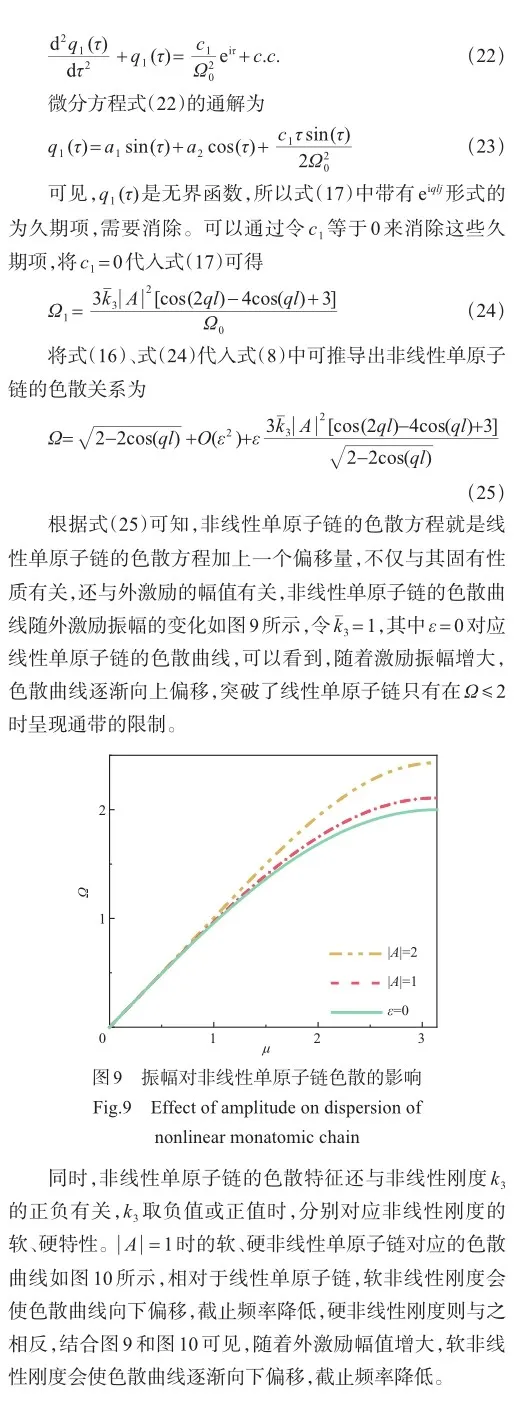
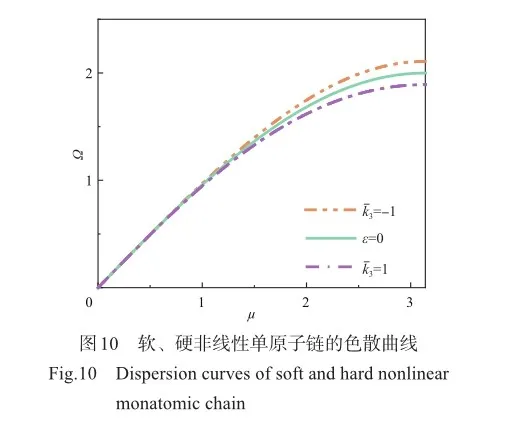
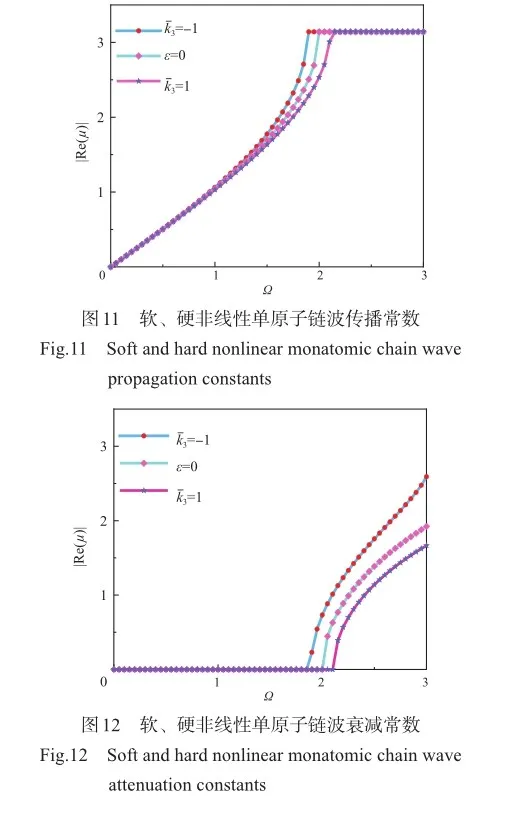
为分析波的衰减，根据式（28），绘出μ的实部和虚部随Ω变化的曲线，分别如图11和图12所示。根据图11可以看出，相对于线性单原子链，软非线性会使传播常数向Ω减小的方向偏移，降低了截止频率；硬非线性会使传播常数向Ω增大的方向偏移，即增大了截止频率。根据图12可以看出，相对于线性单原子链，软非线性单原子链的波衰减常数曲线向Ω减小的方向偏移，衰减常数变得更大；硬非线性单原子链的波衰减常数曲线向Ω增大的方向偏移，衰减常数变得更小。所以硬非线性更有利于单原子链中波的传播。

对于周期结构，较少周期既可体现出周期特性。经过以上分析，可以采用3～5周期的磁铁，其中两端磁铁需固定以防止受到激励后磁铁无限扩展，同时每隔一定距离将一组周期结构布置在壁板的隔框之间[4，29]，以利用周期结构的截止频率来调控和抑制壁板的低频振动。具体布置到壁板之上的结构振动特性有待进一步研究。

3.2 谐波平衡法

4 结论

本文对由磁力特性构成的一维立方非线性刚度周期结构建立了理论模型，给出了立方非线性刚度周期结构色散关系的求解过程。根据求解结果，对比分析一维线性刚度周期结构和一维立方非线性刚度周期结构的色散特性，得出以下结论：

（1）对于一维线性刚度周期结构，当外激励频率小于截止频率时，结构中波的传播呈现通带，在外激励频率大于截止频率时，波会衰减。

（2）立方非线性刚度周期结构的色散，不仅与其单胞固有频率有关，还与外激励的幅值有关，外激励幅值越大，色散曲线偏移量越大。相较于线性刚度周期结构，硬非线性可以突破线性离散周期结构外激励频率大于固有频率的两倍时波就衰减的限制，进一步拓宽通带宽度，软非线性则相反。

（3）对于一维立方非线性刚度周期结构色散关系的求解，摄动法和谐波平衡法的求解结果只差一个高阶小量，忽略高阶小量可认为求解结果相同。

综上所述，本文的研究和结论将为立方非线性刚度周期结构的设计提供理论指导，为基于非线性振子周期结构的飞行器壁板振动控制的进一步研究奠定基础，后续工作将利用磁铁串联形成周期结构后开展试验研究，验证本文推导结果。

参考文献

[1]张君贤， 瞿叶高， 谢方涛，等. 强噪声作用下复合材料壁板气动弹性摩擦非线性振动[J]. 振动与冲击， 2021， 40（13）： 216-221+270. Zhang Junxian， Qu Yegao， Xie Fangtao， et al. Aeroelastic friction nonlinear vibration of composite panels under strong noise[J]. Journal of Vibration and Shock， 2021， 40（13）： 216-221+270.（in Chinese）

[2]张肖肖，张赐宝，秦强，等.基于实测数据的复合材料层合板热导率预测方法[J].航空科学技术，2022，33（6）： 14-19.Zhang Xiaoxiao， Zhang Cibao， Qin Qiang， et al. Thermal conductivity prediction method for composite laminates based on measured data[J]. Aeronautical Science & Technology， 2022， 33（6）： 14-19. （in Chinese）

[3]潘杰，原崇新，李志远，等.考虑可制造性的变刚度复合材料加筋壁板的优化设计[J].航空科学技术，2023，34（3）： 64-70. Pan Jie， Yuan Chongxin， Li Zhiyuan， et al. Optimised design of variable stiffness composite reinforced wall plate considering manufacturability[J]. Aeronautical Science & Technology， 2023， 34（3）：64-70. （in Chinese）

[4]李寅. 基于声学超材料的飞机壁板低频减振降噪设计研究[D].长沙： 国防科技大学， 2018. Li Yin. Research on low frequency vibration and noise reduc‐tion design of aircraft panel based on acoustic metamaterials[D]. Changsha： National University of Defense Technology， 2018.（in Chinese）

[5]徐鉴. 振动控制研究进展综述[J]. 力学季刊， 2015， 36（4）： 547-565. Xu Jian. Review on research progress of vibration control[J]. Quarterly Journal of Mechanics， 2015， 36（4）： 547-565.（in Chinese）

[6]Gendelman O V. Transition of energy to a nonlinear localized mode in a highly asymmetric system of two oscillators[J]. Nonlinear Dynamics， 2001， 25（1-3）： 237-253.

[7]温激鸿. 人工周期结构中弹性波的传播：振动与声学特性[M].北京：科学出版社， 2015. Wen Jihong. Propagation of elastic waves in artificial periodic structures： Vibration and acoustic characteristics[M]. Beijing： Science Press， 2015.（in Chinese）

[8]Mead D M. Wave propagation in continuous periodic structures： Research contributions from Southampton：1964—1995[J]. Journal of Sound and Vibration， 1996， 190（3）： 495-524.

[9]Abrahamson A L. The response of periodic structures to aeroacoustic pressures， with particular reference to aircraft skin-rib spar structures[D]. Southampton： University of Southampton， 1973.

[10]Orris R M， Petyt M. A finite element study of harmonic wave propagation in periodic structures[J]. Journal of Sound and Vibration， 1974， 33（2）： 223-236.

[11]Ampatzidis T， Leach R K， Tuck C J， et al. Band gap behaviour of optimal one-dimensional composite structures with an additive manufactured stiffener[J]. Composites Part B： Engineering， 2018， 153： 26-35.

[12]Ewins D J. Vibration characteristics of bladed disc assemblies[J]. Journal of Mechanical Engineering Science， 1973， 15（3）： 165-186.

[13]Deshpande V S， Fleck N A. High strain rate compressive behaviour of aluminium alloy foams[J]. International Journal of Impact Engineering， 2000， 24（3）： 277-298.

[14]Talbot J P， Hunt H E M. A computationally efficient piledfoundation model for studying the effects of ground-borne vibration on buildings[J]. Proceedings of the Institution of Mechanical Engineers， Part C： Journal of Mechanical Engineering Science， 2003， 217（9）： 975-989.

[15]Bao Jing， Shi Zhifei， Xiang Hongjun. Dynamic responses of a structure with periodic foundations[J]. Journal of Engineering Mechanics， 2012， 138（7）： 761-769.

[16]Brun M， Movchan A B， Jones I S. Phononic band gap systems in structural mechanics： finite slender elastic structures and infinite periodic waveguides[J]. Journal of Vibration and Acoustics， 2013， 135（4）： 041013.

[17]Banerjee A， Das R， Calius E P. Waves in structured mediums or metamaterials： a review[J]. Archives of Computational Methods in Engineering， 2019， 26： 1029-1058.

[18]王凯，周加喜，蔡昌琦，等. 低频弹性波超材料的若干进展[J].力学学报， 2022， 54（10）： 2678-2694. Wang Kai， Zhou Jiaxi， Cai Changqi， et al. Review of low-frequen‐cy elastic wave metamaterials[J]. Chinese Journal of Theoretical and Applied Mechanics， 2022， 54（10）： 2678-2694.（in Chinese）

[19]高明，吴志强. 一维三振子周期结构带隙设计[J]. 物理学报， 2013， 62（14）： 86-92. Gao Ming， Wu Zhiqiang. Band gap design for one-dimensional periodic structure with three oscillators[J]. Acta Physica Sinica， 2013， 62（14）： 86-92.（in Chinese）

[20]武恒星， 娄佳. 含双质量谐振单元的声学超材料杆的纵波传播[J]. 哈尔滨工程大学学报，2022， 43（9）： 1349-1355. Wu Hengxing， Lou Jia. Propagation of longitudinal waves in an acoustic metamaterial rod with bi-mass resonant units[J]. Journal of Harbin Engineering University， 2022， 43（9）： 1349-1355.（in Chinese）

[21]Fronk M D， Fang Lezheng， Packo P， et al. Elastic wave propagation in weakly nonlinear media and metamaterials： a review of recent developments[M]. Berlin： Springer， 2023.

[22]位琳帅. 颗粒非线性弹性波超材料的带隙与非互易传输特性[D]. 北京： 北京交通大学， 2021. Wei Linshuai. Band gap and nonreciprocal transmission characteristics of granular nonlinear elastic wave metamaterials[D].Beijing： Beijing Jiaotong University， 2021.（in Chinese）

[23]Narisetti R K， Leamy M J， Ruzzene M. A perturbation approach for predicting wave propagation in one-dimensio nal nonlinear periodic structures[J]. Journal of Vibration and Acoustics， 2010， 132（3）： 0310011.

[24]刘延柱， 陈立群. 非线性振动[M].北京：高等教育出版社， 2001. Liu Yanzhu， Chen Liqun. Nonlinear vibration[M]. Beijing： Higher Education Press， 2001.（in Chinese）

[25]Ding Hu， Chen Liqun. Designs， analysis， and applications of nonlinear energy sinks[J]. Nonlinear Dynamics， 2020， 100（4）： 3061-3107.

[26]Olaru R， Arcire A， Petrescu C， et al. A novel vibration actuator based on active magnetic spring[J]. Sensors and Actuators A： Physical， 2017， 264： 11-17.

[27]韩超，刘桂祥，邵骁麟，等.准零刚度隔振器非线性削弱方法研究[J].核动力工程，2022，43（S1）：121-126. Han Chao， Liu Guixiang， Shao Xiaolin， et al. Study on nonlinear weakening method of quasi-zero stiffness vibration isolator[J]. Nuclear Power Engineering，2022，43（S1）：121-126.（in Chinese）

[28]Brillouin L. Wave propagation in periodic structures： electric fil‐ters and crystal lattices[M]. New York： Dover publications， 1953.

[29]Fang Xin， Wen Jihong， Bonello B， et al. Ultra-low and ultrabroad-band nonlinear acoustic metamaterials[J]. Nature com‐munications， 2017， 8（1）： 1288.

Study on Dispersion Characteristics of One-Dimensional Cubic Nonlinear Stiffness Periodic Structures

Zuo Ang1， Xu Yanlong1，2， Chen Ning1， Zhang Mengjia1， Gu Yingsong1， Yang Zhichun1

1. Northwestern Polytechnical University， Xi’an 710072， China

2. State Key Laboratory for Strength and Vibration of Mechanical Structures， Xi’an 710049，China

Abstract： The study of the dispersion characteristics of periodic structures formed by cubic nonlinear stiffness unit cell arrays， which has a certain promoting effect on the research of aircraft panel vibration control. Firstly， the dynamic model of one-dimensional linear stiffness periodic structure is constructed， and its dispersion equation is derived based on Bloch theory. Its dispersion characteristics and wave propagation are analyzed. Then the dynamic model of the periodic structure with cubic nonlinear stiffness unit cells is established， and the dispersion equation of the periodic structure is derived by using the perturbation approach. Finally， considering the complex working environment of aircraft panels and the limitation that the perturbation approach is only applicable to weak nonlinearity， the solution process of harmonic balance method for periodic structures with cubic nonlinear stiffness dispersion relation is given， and the solution results of the two methods are compared. This paper lays the foundation for further research on vibration control of aircraft wall panels using nonlinear periodic structures， and also contributes to the research on lowfrequency damping of nonlinear phononic crystals.

Key Words： periodic structure； dispersion characteristics； perturbation approach； harmonic balance method； nonlinear