展弦比对NACA0012弹性平直机翼颤振临界特性影响研究

摘 要：展弦比是飞行器机翼设计的重要参数，研究其对机翼颤振临界特性的影响具有重要的工程应用价值。本文采用三维雷诺平均N-S方程和S-A湍流模型求解NACA0012弹性平直机翼的非定常气动力，结合由模态法建立的机翼结构动力学方程，发展了计算流体力学（CFD）/计算结构力学（CSD）颤振时域数值模拟方法。利用该方法研究了不同展弦比条件下机翼的颤振临界速度和频率。结果表明，由于展弦比较大且材质轻柔，机翼会出现一定幅度的垂向静弯曲变形。展弦比的增大不会影响机翼模态固有振型，但是会导致机翼颤振临界速度、颤振频率和模态固有频率的降低。

关键词：展弦比； 颤振临界特性； 弹性平直机翼； 模态； 数值模拟

中图分类号：V215.34 文献标识码：A DOI：10.19452/j.issn1007-5453.2024.06.006

基金项目： 航空科学基金（201958058001）；中国空气动力研究与发展中心旋翼空气动力学重点实验室研究开放课题（RAL202204-9）

机翼展弦比的定义是展长b与平均弦长cmean的比值，也可以表示为展长的平方b2与参考面积S的比值[1]。为了降低诱导阻力，提高升阻比和任务载荷，高空长航时无人机、大型运输机和大型客机等飞行器在追求结构轻量化的同时，普遍采用展弦比在10以上的大展弦比机翼[2]。然而，轻量化结构和大展弦比设计使得机翼容易与非定常流动进行耦合，诱发出复杂的气动弹性问题，如颤振、弯曲和扭转发散等[3]，不仅影响飞行器的运行性能，还可能导致机翼产生疲劳损坏甚至结构破坏，产生严重后果[4]。因此，大展弦比弹性机翼颤振分析对于提高飞行器的稳定性和安全性具有重要意义。

颤振临界特性（即颤振临界速度和频率）的预测是机翼颤振分析的重要部分。对于飞行器机翼而言，随着来流速度U￥的增大，在一定U￥范围内，由气流扰动引起的振动会衰减。当U￥达到某一临界值时，机翼振动幅值刚好维持不变，这一速度在颤振分析中被称为颤振临界速度Uf，等幅振动的频率即为颤振频率ωf。当U￥超过Uf后，振动会发散，机翼会发生颤振[5]。当前，大展弦比弹性机翼颤振临界特性的研究主要涉及两个科学问题：（1）颤振分析方法的构造和验证；（2）外挂载荷分布[6]、根部迎角[7]、操纵面及其偏转角[8]、材料刚度[9]和密度[10]等对机翼颤振临界特性的影响。速度-阻尼比外推法[11]、颤振裕度法[12]和p-k法[13]均为学术界和工程界中常用的颤振分析方法。然而，这些方法采用的气动力计算手段（如西奥道森模型、涡格法和偶极子格网法等）大多基于势流理论，未考虑气体的黏性效应。近年来，随着计算机性能的发展和大规模并行计算的普及，以N-S方程为基础的计算流体力学（CFD）/计算结构力学（CSD）时域数值模拟方法[14]已广泛应用于飞行器机翼的设计。CFD/CSD方法直接从流体和结构基本方程出发，合理性和可靠性较高，而且除了颤振临界速度和频率以外，还能够获得振动响应、瞬时气动力和流场等信息。

综上所述，现有的大展弦比弹性机翼颤振临界特性研究大多在特定展弦比条件下开展，鲜有涉及展弦比对机翼颤振临界速度和频率的影响。本文以大展弦比NACA0012弹性平直机翼为研究对象，采用模态法进行机翼的结构动力学分析，结合三维雷诺平均N-S方程和S-A湍流模型[15]，建立了CFD/CSD颤振时域数值模拟方法。利用该方法对机翼颤振临界速度和频率随展弦比的变化规律进行研究。

1 CFD/CSD颤振时域数值模拟方法

1.1 流动控制方程

本文采用自研CFD软件求解大展弦比NACA0012弹性平直机翼的非定常气动力，其控制方程为积分形式的守恒型三维非定常雷诺平均N-S方程，直角坐标系下的形式为

采用基于预估-校正技术的四阶杂交线性多步法[17]对式（4）进行时域推进求解。

图1给出了大展弦比NACA0012弹性平直机翼颤振时域数值模拟流程图。可以看出，机翼的结构参数矩阵M、G和K和固有振型由有限元模态分析获得，气动力矩阵F由CFD数值模拟确定。一般而言，翼面的CFD网格点和模态分析控制点是不重合的，因此在每一个时间步内，需要通过结构固有振型在翼面处进行数据传递：压力分布通过振型转化为广义气动力，进而求解机翼结构力学方程获得广义位移，广义位移再通过振型转化为翼面物理位移，作为下一个时间步CFD求解的边界条件。模态分析得到的结构固有振型通过径向基函数插值法[18]转化为翼面CFD网格点描述下的振型分布。机翼振动后CFD网格的变形和运动也采用基于径向基函数插值的动网格技术[19]实现。

1.3 算例验证

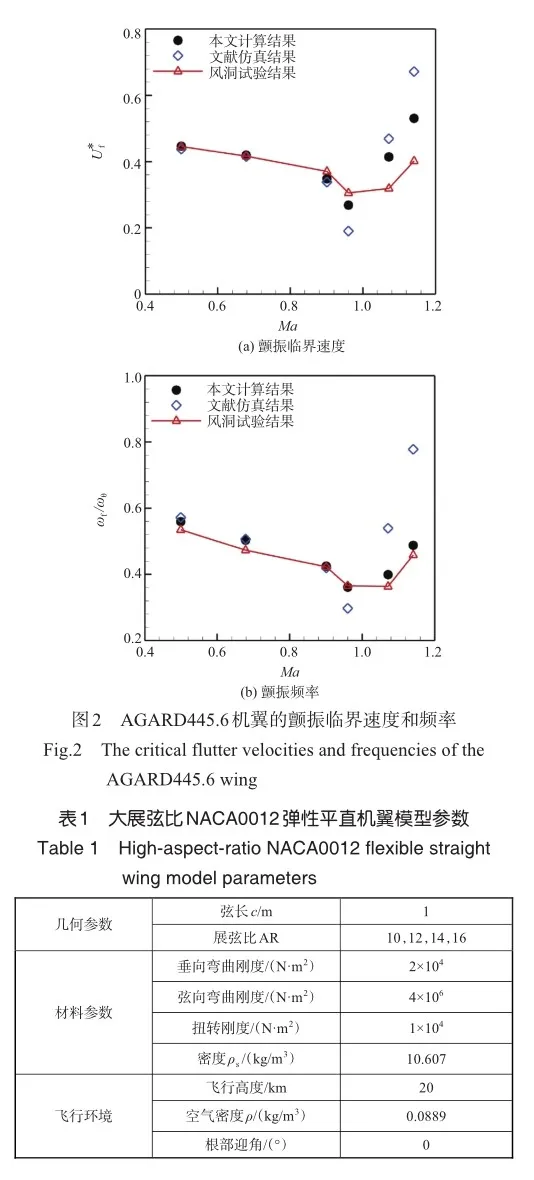
AGARD445.6机翼颤振特性风洞试验是由美国国家航空航天局（NASA）兰利研究中心完成的。目前，该机翼模型已成为国际上颤振程序考核的标准三维算例。

该机翼模型的几何参数为：展弦比为1.644，根梢比为1.517，1/4弦线后掠角为45°，翼型为NACA65A004。机翼试验模型的材料为桃花心木。机翼颤振分析取前四阶振动模态，其固有振型依次为一阶垂向弯曲、一阶扭转、二阶垂向弯曲和二阶扭转。

2 结果与分析

本文的研究重点在于展弦比对NACA0012弹性平直机翼颤振临界特性（即颤振临界速度和频率）的影响。机翼模型的几何参数、材料参数和飞行环境见表1，考虑10、12、14和16的4个展弦比AR工况。颤振数值模拟取前五阶振动模态，图3给出了不同展弦比条件下机翼模态固有频率。从图3中可以看出，随着展弦比的增大，机翼模态固有振型不变，固有频率逐渐降低。机翼的第一、二和五阶振动模态为垂向弯曲模态，第三阶为扭转模态，第四阶则为弦向弯曲模态。

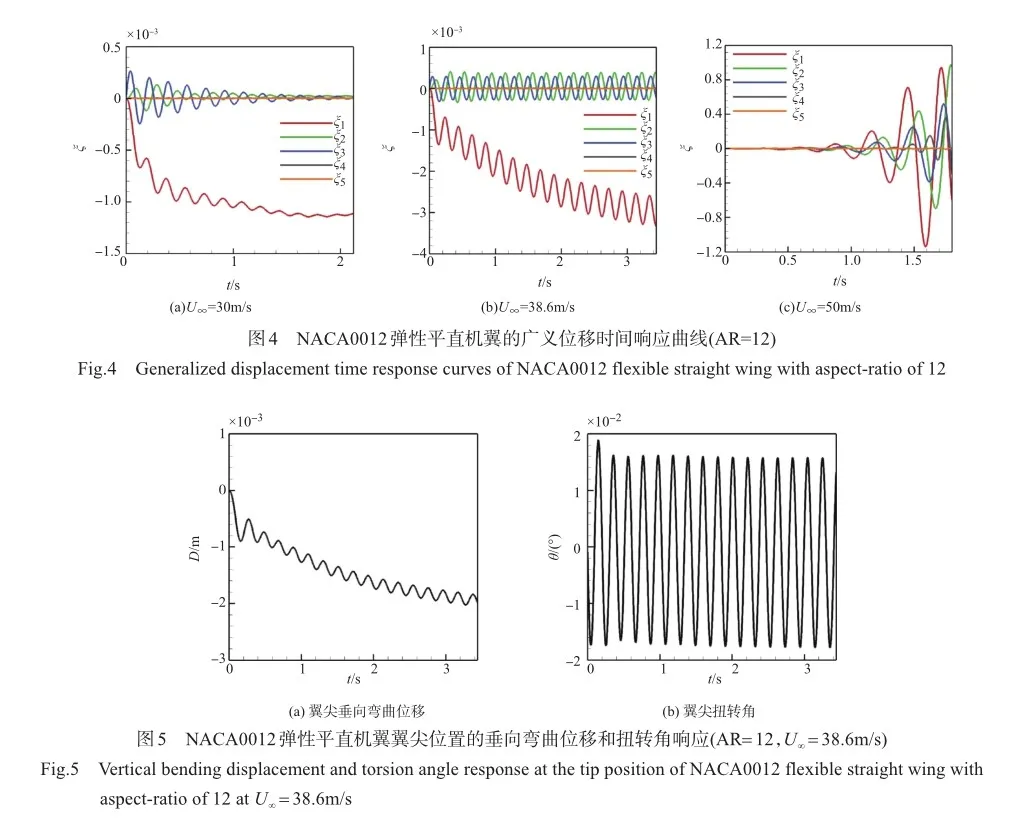
以展弦比AR=12工况为例，图4给出了不同来流速度U￥时NACA0012弹性平直机翼的广义位移时间响应曲线。可以看出，当U￥=30m/s和38.6m/s时，第一阶振动模态广义位移（ξ1）存在一定幅度的静漂移，说明由于展弦比较大，且材质轻柔，机翼发生了垂向静弯曲变形。当U￥=30m/s时，各阶模态广义位移响应表现为振动衰减。当U￥提高至38.6m/s时，广义位移均表现为近似等幅响应。进一步提高U￥至50m/s时，广义位移表现出明显的振动发散趋势。综合以上数值模拟结果可以得出，机翼在U￥=38.6m/s时处于临界稳定状态，即AR=12时，机翼的颤振临界速度Uf= 38.6m/s。

利用结构固有振型将机翼的广义位移转化为翼面物理位移。图5给出了AR=12的NACA0012弹性平直机翼在颤振速度（Uf=38.6m/s）时翼尖位置的垂向弯曲位移（以向上为正）和扭转角响应。图6则给出了翼尖响应的快速傅立叶变换（FFT）频谱。可以看出，垂向弯曲位移的平衡位置不为0，而扭转角的平衡位置为0°，表明机翼在垂向出现了静弯曲变形。机翼的振动幅值随时间t基本保持不变，翼尖弯曲位移和扭转角的主频率均为31.04rad/s。因此，可以得出，AR=12时，机翼的颤振频率ωf=31.04rad/s。

采用颤振数值模拟方法对其他AR条件下NACA0012弹性平直机翼的颤振临界特性进行计算，图7给出了机翼颤振临界速度和频率随展弦比的变化趋势。可以看出，当AR从10增大至16，机翼的颤振临界速度会减小约45.71%，而颤振频率会减小约33.16%。说明了AR的增大会引起机翼颤振临界速度和频率的降低。

3 结论

本文采用以三维雷诺平均N-S方程和S-A湍流模型为基础的CFD数值模拟方法求解NACA0012弹性平直机翼的非定常气动力，结合模态法构造的机翼结构动力学方程，发展了CFD/CSD颤振时域数值模拟方法，进而研究了展弦比对机翼颤振临界特性的影响，主要得到以下结论：

（1）由于展弦比较大，且材质轻柔，机翼在垂向上会发生一定幅度的静弯曲变形。

（2）机翼展弦比的增大不会带来结构模态固有振型的变化，但是会降低颤振临界速度、颤振频率和结构模态固有频率。

参考文献

[1]吴子牛， 白晨媛， 李娟， 等. 空气动力学[M]. 北京： 北京航空航天大学出版社， 2016. Wu Ziniu， Bai Chenyuan， Li Juan， et al. Aerodynamics[M]. Beijing： Beihang University Press， 2016.（in Chinese）

[2]刘国春. 大展弦比机翼气动外形设计方案研究[J]. 飞机设计， 2011， 31（3）： 9-12+36. Liu Guochun. Research on design of high aspect wing shape[J]. Aircraft Design， 2011， 31（3）： 9-12+36. （in Chinese）

[3]Afonso F， Vale J， Oliveira é， et al. A review on non-linear aero‐elasticity of high aspect-ratio wings[J].Progress in Aerospace Sciences， 2017， 89： 40-57.

[4]Arena A， Lacarbonara W， Marzocca P. Nonlinear aeroelastic formulation and postflutter analysis of flexible high-aspectratio wings[J]. Journal of Aircraft， 2013， 50（6）： 1748-1764.

[5]杨超. 飞行器气动弹性原理[M]. 2版. 北京： 北京航空航天大学出版社， 2016. Yang Chao. Aeroelastic principle of aircraft[M]. 2ed edition. Beijing： Beihang University Press， 2016.（in Chinese）

[6]祁武超， 张贺铭， 田素梅， 等. 外挂物对大展弦比直机翼颤振特性的影响[J]. 计算力学学报， 2022， 39（5）： 598-607. Qi Wuchao， Zhang Heming， Tian Sumei， et al. Effects of external stores on flutter characteristics of a straight wing with high aspect ratio[J]. Chinese Journal of Computational Mechanics， 2022， 39（5）： 598-607. （in Chinese）

[7]付志超， 陈占军， 刘子强. 大展弦比机翼气动弹性的几何非线性效应[J]. 工程力学， 2017， 34（4）： 231-240. Fu Zhichao， Chen Zhanjun， Liu Ziqiang. Geometric nonlinear aeroelastic behavior of high aspect ratio wings[J]. Engineering Mechanics， 2017， 34（4）： 231-240. （in Chinese）

[8]胡志勇， 党云卿， 陈海. 副翼偏转角对大展弦比机翼颤振特性的影响研究[J]. 航空科学技术， 2016， 27（9）： 12-16. Hu Zhiyong， Dang Yunqing， Chen Hai. Influence of aileron de‐flection on the flutter of high-aspect-ratio wings[J]. Aeronauti‐cal Science & Technology， 2016， 27（9）： 12-16. （in Chinese）

[9]Qiao Shengjun， Jin Jiao， Ni Yangge， et al. Effect of stiffness on flutter of composite wings with high aspect ratio[J]. Mathemati‐cal Problems in Engineering， 2021， 2021： 1-14.

[10]余秋阳， 李兴华， 李新涛， 等. 大展弦比NACA0012弹性平直机翼颤振特性研究[J]. 西北工业大学学报， 2022， 40（5）： 1071-1079. Yu Qiuyang， Li Xinghua， Li Xintao， et al. Study on flutter char‐acteristics of NACA0012 flexible straight wing with high-as‐pect-ratio[J]. Journal of Northwestern Polytechnical Universi‐ty， 2022， 40（5）： 1071-1079. （in Chinese）

[11]胡家亮， 吴江鹏， 脱朝智， 等. 3D打印飞机颤振风洞试验模型设计与应用[J]. 航空科学技术， 2022， 33（9）： 43-50. Hu Jialiang， Wu Jiangpeng， Tuo Chaozhi， et al. Design and application of 3D printed aircraft flutter wind tunnel test model[J]. Aeronautical Science & Technology， 2022， 33（9）： 43-50.（in Chinese）

[12]Zimmerman N H， Weissenburger J T. Prediction of flutter onset speed based on flight testing at subcritical speeds[J]. Journal of Aircraft， 1964， 1（4）： 190-202.

[13]Li Xing， Bai Yuguang， Xiao Ling， et al. Vibration control studies of a high-aspect-ratio wing with geometric nonlinearity[J]. Aerospace Science and Technology， 2022， 123： 107461.

[14]张科施， 凌圣博， 韩忠华. 跨声速运输机机翼气动/结构优化平台AeroStruct的发展及应用[J]. 航空科学技术， 2022， 33（4）： 47-56. Zhang Keshi， Ling Shengbo， Han Zhonghua. Development and application of Aerostruct，an aerodynamic/structural optimiza‐tion platform for transonic transport aircraft wings[J]. Aero‐nautical Science & Technology， 2022， 33（4）： 47-56.（in Chinese）

[15]Spalart P R， Allmaras S R. A one-equation turbulence model for aerodynamic flows[J]. La Recherche Aérospatiale， 1994， 1： 5-21.

[16]叶正寅， 王刚， 张伟伟. 流固耦合力学基础及其应用[M]. 2版. 哈尔滨： 哈尔滨工业大学出版社， 2016. Ye Zhengyin， Wang Gang， Zhang Weiwei. Fundamentals of fluid-structure coupling and its application[M]. 2nd edition. Harbin： Harbin Institute of Technology Press， 2016. （in Chinese）

[17]Zhang Weiwei， Jiang Yuewen， Ye Zhengyin. Two better loosely coupled solution algorithms of CFD based aeroelastic simula‐tion[J]. Engineering Applications of Computational Fluid Me‐chanics， 2007， 1（4）： 253-262.

[18]Wright G B. Radial basis function interpolation： numerical and analytical developments[D]. Boulder： University of Colorado at Boulder， 2003.

[19]De Boer A， Van der Schoot M S， Bijl H. Mesh deformation based on radial basis function interpolation[J]. Computers & structures， 2007， 85（11-14）： 784-795.

[20]Yates E C J. AGARD standard aeroelastic configurations for dynamic response I：wing 445.6[R]. NASA-TM-100492， 1987.

[21]Silva W A， Lii B P， Chwalowski P. Evaluation of linear， inviscid， viscous， and reduced-order modelling aeroelastic solutions of the AGARD 445.6 wing using root locus analysis[J]. International Journal of Computational Fluid Dynamics， 2014， 28（3）： 122-139.

Effect of Aspect-ratio on Flutter Critical Characteristics of NACA0012 Flexible Straight Wing

Yu Qiuyang， Xu Shengjin

Tsinghua University， Beijing 100084， China

Abstract： Aspect-ratio is an important parameter in the design of aircraft wings， and studying its influence on the flutter critical characteristics of wings has significant engineering application value. This paper uses the threedimensional Reynolds Averaged N-S equations and the S-A turbulence model to solve the unsteady aerodynamic forces of high-aspect-ratio NACA0012 flexible straight wings. Combining with the wing dynamic equation established by the modal method， a CFD/CSD flutter time-domain numerical simulation method is developed. This method is employed to study the influence of aspect-ratio on the flutter critical characteristics of the wing. The results indicate that due to the high-aspect-ratio and soft material， the wing has a certain range of vertical static bending deformation. The increase in aspect-ratio does not affect the natural mode shape of the wing， but reduces the modal natural frequency， flutter critical velocity， and flutter frequency.

Key Words： aspect-ratio； flutter critical characteristics； flexible straight wing； mode； numerical simulation