基于地震频率域数据的改进非局部均值去噪研究

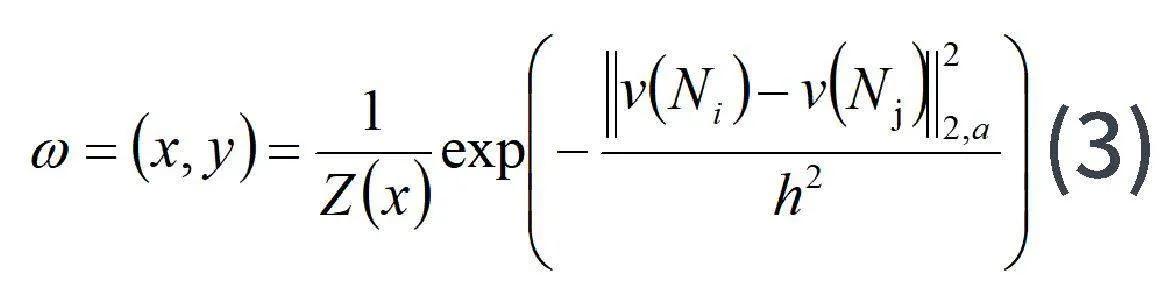
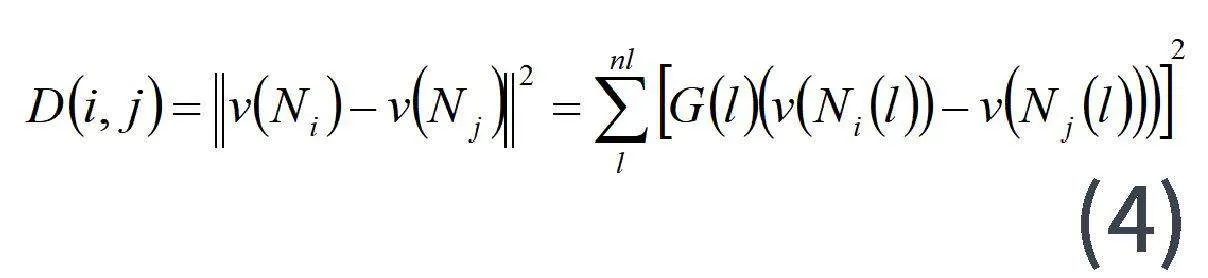
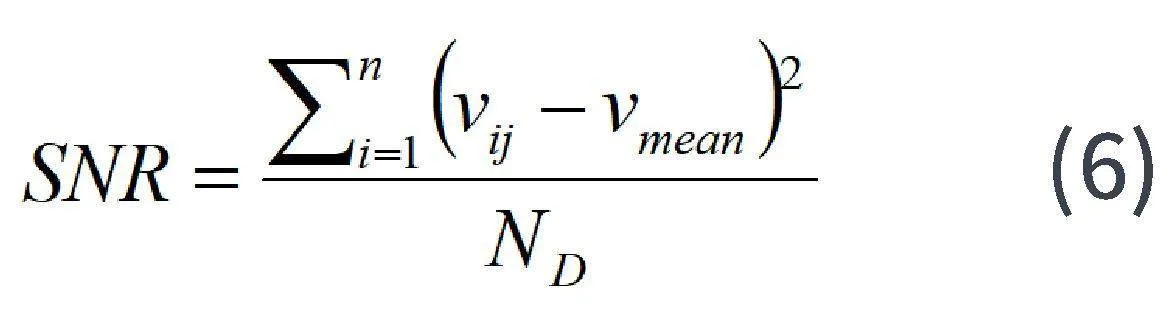
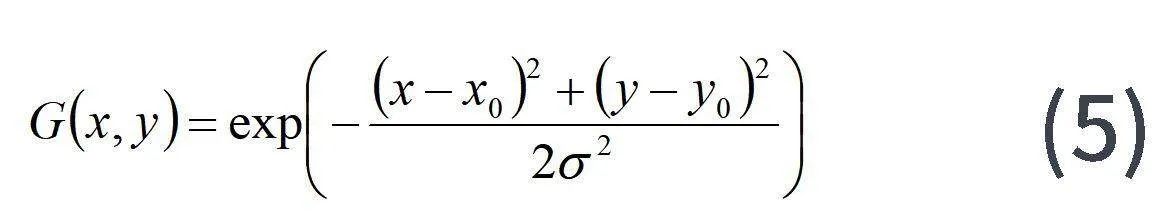
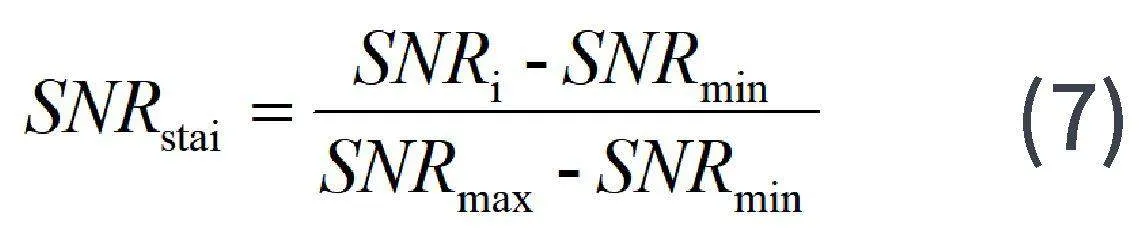
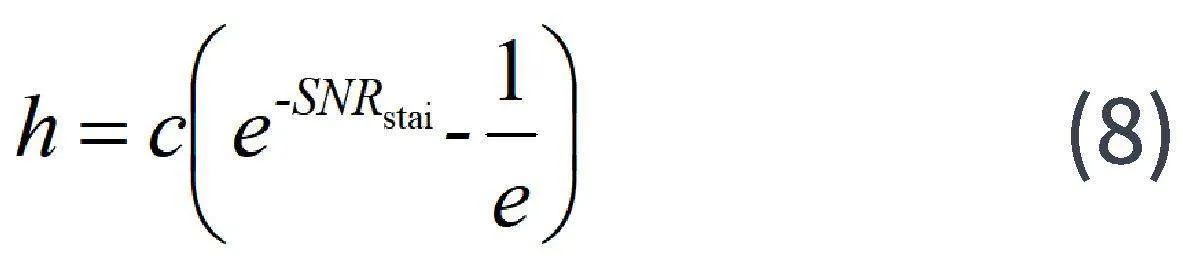
摘 要：油气勘探地震资料中常常存在严重噪音，常规的去噪方法在去噪中无法对地震主频段内的型号进行针对性处理，对区域目标处的去噪强度过于均匀，信噪比保留能力不高，容易形成整体去噪过渡平滑。针对以上问题，提出采用频率域切片和改进非局部均值去噪的方法进行解决。首先通过傅里叶变换将地震数据变换到频率域，然后对其实部、虚部切片进行排序，通过改进后的自适应平滑滤波因子对切片进行滤波，再通过傅里叶反变换实现将滤波后的频率数据恢复到时间域。通过实验得出去噪后的效果能比较完整的保留地震道集的主要特征，平面剖面特征保留完整。

关键词：地震资料去噪；傅里叶变换；非局部均值；自适应

1.引言

地震数据中噪声来源于地震数据采集、传输、压缩等方面[1][2]，噪声的种类也各不相同，比如随机噪声、高斯噪声等，噪音的存在会严重影响后续地震资料的处理，因此在常规的子波处理、速度分析之前需要进行叠前噪音消除，线性切除是最简单、最直接的去噪方式之一，对相干噪音的消除效果好，但存在时间域去噪不可逆的特性，并且切除的数据量不易约束[3][4]。小波变换分频可以逐点对相干干扰方向进行扫描，对直线变换的干扰有较好的去噪效果。由于小波变换分频只能在有限的频带进行去噪，其计算原理是在数据上直接做减法，会导致剖面上能量不均，因此用小波变换分频去噪还需要在去噪后进行其他修饰处理，整体效果并不良好[5][6]。

针对以上问题，本文提出用基于T-XY域的非局部均值去噪方法进行地震噪音去除。该方法通过切片数据，降低对特定频率切片的去噪数据计算效率，同时通过高斯加权欧氏距离代替欧式距离能有效的提高去噪效果，最后加入自适应平滑参数，控制窗口下的局部滤波强度。

2.地震去噪原理

对于输入的带有噪声的数据v（x），其加噪声数据可以用以下方程来表示：

其中：u（x）是原始没有噪声的图像。x是像素集合，η（x）是加噪声项，代表噪声带来的影响。Ω是像素的集合，是整个地震数据体。噪声是直接叠加在原始数据上的，这个噪声来源比较多，可以是随机噪声、高斯噪声。理论上来说，如果能够精确地获得噪声，用输入数据减去噪声就可以恢复出原始数据。但实际地震资料处理中，除非明确地知道噪声生成的方式，否则噪声很难单独求出来。

地震资料处理中，噪声常常用高斯噪声N（μ，σ2）来近似表示，其中μ=0，σ2是噪声的方差，σ2越大，表示噪声越大。去噪部分计算思想是对高斯噪声数据求平均，即对N个时窗内相近的数据求平均，其结果将使得高斯噪声的方差降低到原来的N分之一。去噪过程可以用下面公式来表示：

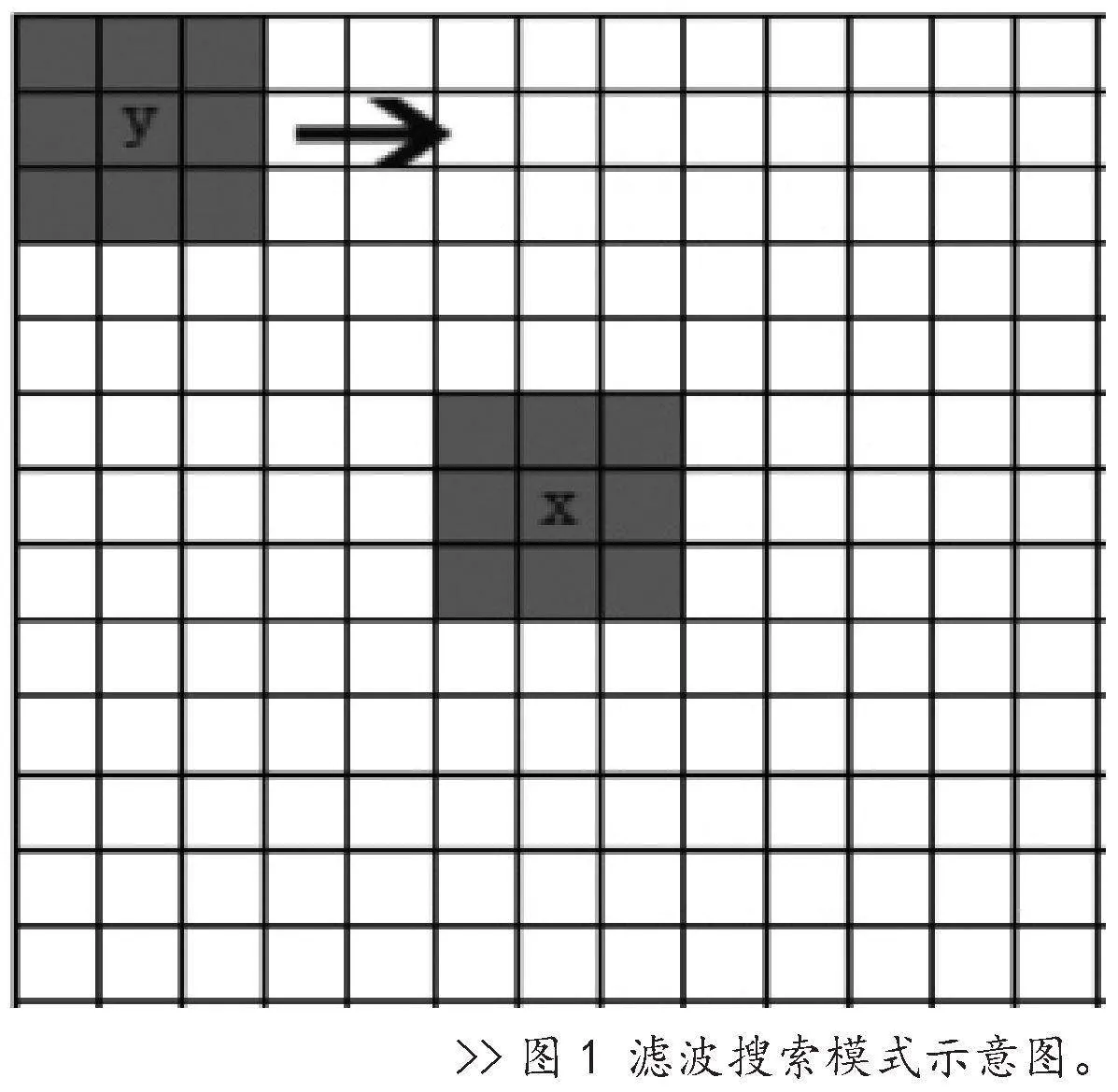
去噪过程为：开两个窗口进行数据处理，其中一个窗口是大窗D，其含义为将数据分为N个D大小的窗口，其意义为：在D窗口中，设置一个小的搜索窗口y（d×d）和一个中心窗口x（d×d），如图1所示。两个窗口的中心分别为y和x，搜索窗口y（d×d）在D窗口中进行移动，并与中心窗口x（d×d）进行相似程度的计算，其权重ω（x，y）计算方法为：

以ν（Ni）、ν（Nj）表示矩形邻域，计算两个邻域的二范数；h为平滑因子，Z（x）为归一化系数。

以相近两个区域的高斯加权欧氏距离代替传统的欧式距离计算表达式得到新的系数表达式为：

G（l）表示具有标准差为σ的高斯核，l代表邻域内nl个元素之一。

（x0，y0）代表高斯核的中心，（x，y）代表所计算的l点的位置坐标。该方法能将近邻域的点赋予更高的权重。

平滑因子的选择采用自适应方式，对区域D中的数据求区域信噪比SNR。SNR的计算采用扫描区域D中的能量：

νij，νmean分别为区域D中位于（i，j）位置的能量和区域D中的平均能量。ND为区域D中所有的可分移动小窗口总数。

对区域信噪比SNR进行归一化处理：

平滑因子h表达式为：

c为平滑阈值约束参数，在此取50。至此获得每个窗口的权重系数。

3.基于Fourier变换的F-XY域改进NML滤波

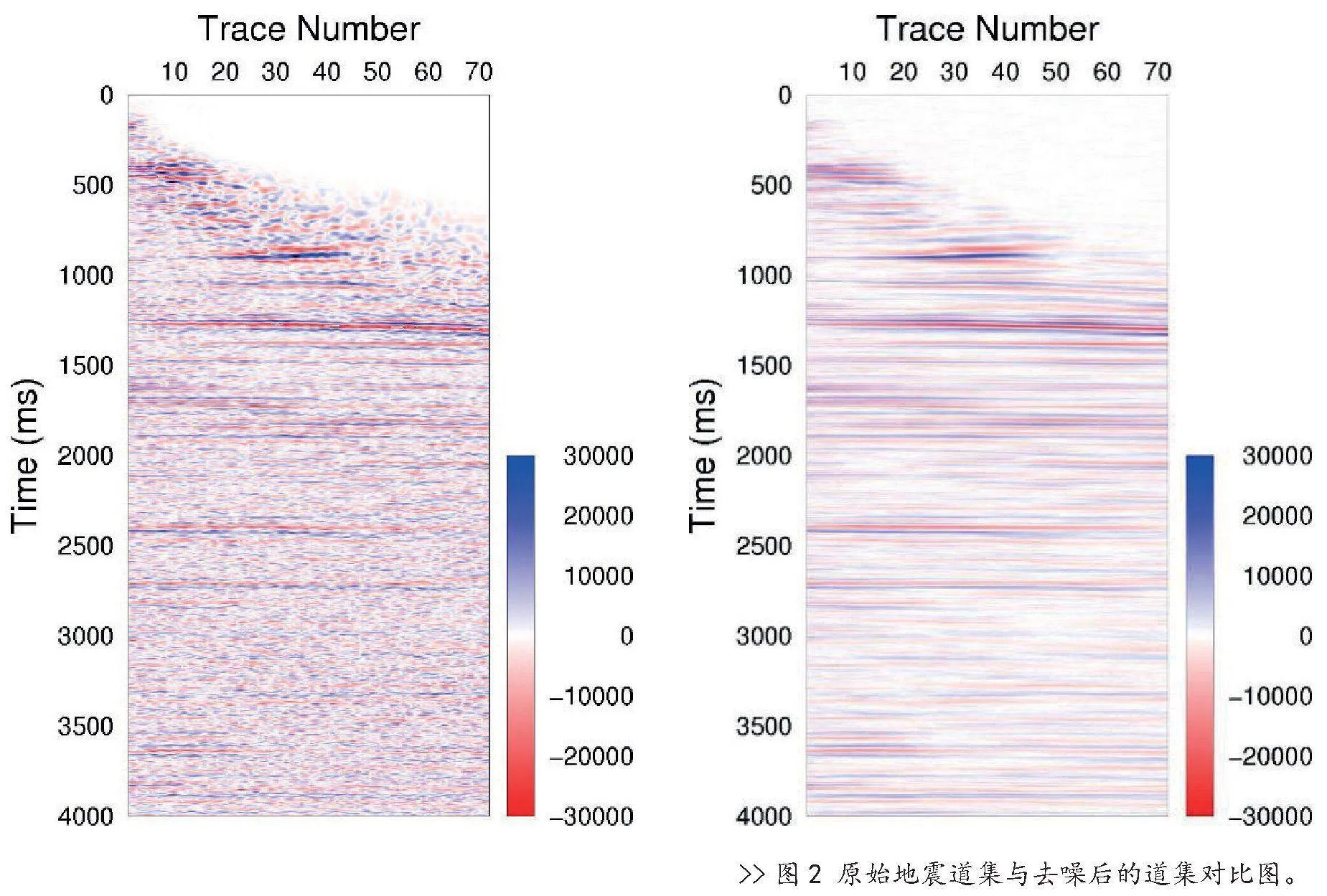
以地震数据T-XY为例，在时间方向进行Fourier变换，其中X代表炮号或者CMP号，Y代表道号或者炮检距，T代表地震数据的时间深度，经过Fourier变换后频率切片fi的实部和虚部进行改进NLM算法去噪，计算自适应平滑因子，经过频率域滤波后，进行Fourier反变化，获得改进NML滤波后的地震数据（FXY-NML），如图2所示。

从地震道集和地震平剖面数据图（图3）可以看出，基于频率域地震数据改进后的NML滤波效果能有效的对地震数据进行滤波，且计算后的数据能比较完整的保持原始数据的主要特征。

4.结论

地震资料是一个庞大的多维数据体，在去噪中不仅要考虑去噪方法的新颖性，同时还需要考虑庞大地震数据去噪的计算效率问题。常规去噪方法一般是整个频率段的整体去噪，很难针对每个频率进行分别去噪，而该方法结合频率切片特征进行分别去噪，能最大尺度的保留数据的原始主要特征。其次，去噪中的去噪系数往往都是人工选择的，没有跟随数据的信噪比进行针对性的调整去噪强度，本次研究采用自适应的方式对去噪系数进行优化，以适应不同区域差异性的要求。需要说明的是，由于是地震数据频率域切片滤波，数据量和数据切片计算比较复杂，所耗费的计算时间成本比较高。

参考文献

[1]李晓璐， 周亚同， 何静飞， 翁丽源， 李书华。“全变分”则化非局部均值地震数据降噪[J].Computer Engineering & Science/Jisuanji Gongcheng yu Kexue 42. （2020）， no. 6.

[2]黄英， 文晓涛， 贺振华。地震图像随机噪声的非局部均值去噪法[J]. 断块油气田 20.6 （2013）： 730-732.

[3]王金刚， 安勇， 徐振旺。基于Shearlet变换的非局部均值地震噪声压制[J].物探与化探 47.1 （2023）： 199-207.

[4]崔亚彤， 王胜侯， 蔡忠贤。基于快速自适应非局部均值滤波的地震随机噪声压制方法[J]. 物探与化探 （2022）.

[5]李鑫。基于改进的加权核范数最小化的地震资料去噪方法[J]. Pure Mathematics 13 （2023）： 2614.

[6]孙思亮，刘怀山。基于曲波变换和快速非局部均值的地震数据随机噪声压制[J].工程地球物理学报 18.2 （2021）： 153-161.