让探究之花在解题教学中精彩绽放

［ 摘 要 ］探究是开启学生智慧的钥匙，是提高课堂教学有效性的重要手段.教学中，教师要为学生营造一个良好的探究环境，重视发挥学生主体和教师主导的作用，通过“一题多变”打开探究之门，让探究之花绽放课堂，点亮人生.

［ 关键词 ］探究；一题多变；绽放课堂

解题是数学教学的重中之重.在传统教学中，部分教师常把数学教学定义为解题教学，可见解题在数学教学中的价值.如何培养和提高学生的解题能力是一个经久不衰的热点话题.笔者认为，在解题教学中，教师应少一些“灌输”，多一些“探究”，引导学生通过观察、实验、探索、交流等活动主动发现问题、提出问题、解决问题，以此促进学生解题能力的提升和思维能力的发展.笔者以复习课中一道典型探究题为例，谈谈自己对解题教学的几点认识，供同行参考.

教学过程

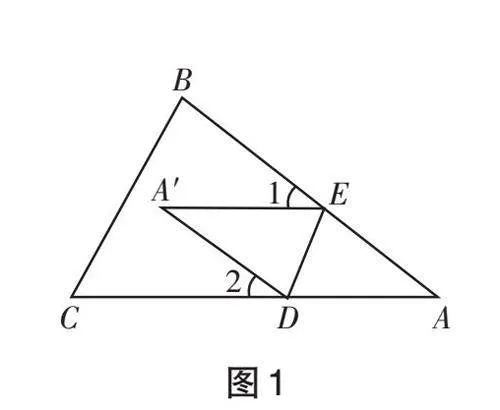
环节1 问题呈现例1 如图1，将 △ABC 纸片沿DE 折叠，使点 A 落在四边形 BCDE内部 A' 的位置，则 ∠1 + ∠2 与 ∠A'之间存在怎样的数量关系？说一说你的理由.（问题①）

问题①给出后，教师没有急于让学生解答，而是鼓励学生“折一折”“画一画”“说一说”.教师在巡视中发现，大多数学生尝试从四边形和三角形内角和中寻找解题的突破口，通过有效互动解决了这个探究问题，但是也有少数学生陷入了沉思，他们迫不及待地想知道解决问题的方法.此时，在学生渴望求知的氛围中，教师带领学生走上探究之旅.

设计意图 例题呈现后，教师没有急于讲授，而是让学生通过动手实践和合作交流探究解决问题的方法，以此提高学生参与课堂的积极性，激发学生探究欲.

环节2 合作探究

师：现在请大家在原来的纸片上继续“折一折”，改变点 A' 落在四边形 BCDE 内的位置，此时 ∠1 ，∠2 和 ∠A' 的大小发生了怎样的变化呢？（问题给出后，学生积极操作、观察、思考、交流）

生 1： ∠A' 的大小始终保持不变， ∠1 和 ∠2 的大小是发生变化的，当 ∠1 变大时 ∠2 变小，当 ∠2 变大时∠1 变小.

教师利用几何画板进行动态演示，让学生进一步观察，获得更加直观的感受.

师：大家想一想，点 A' 除了落在四边形 BCDE 的内部外，还可以落在什么位置呢？请大家试一试.学生积极动手操作，很快就有了新的发现，迫不及待地展示自己的操作成果.

生 2： 点 A' 可 以 落 在 点 B 或点 C 上.

生 3： 点 A' 可 以 落 在 四 边 形BCDE 的四条边上.

生 4：点 A' 还可以落在四边形BCDE 的外部.

……

师：大家真棒.结合大家的发现想一想，以上各种情况是否可以分类呢？

生5：可以分成3类，即点 A' 分别在四边形 BCDE 的内部、外部和边上.

师：非常好，点 A' 在四边形BCDE 的内部的图形已经有了 （如图1），如果让你将另外两种情况用图形表示出来，你会吗？

学生积极思考，通过观察、比较、归纳，画出了另外两种类型的图形（如图2、图3）.

师：图2中， ∠1 与 ∠DA'E 有怎样的数量关系呢？说一说你的理由.（问题②）

该问题不难，教师让学生自主探究，然后点名让学生板演证明过程，教师点评.

师：大家利用三角形外角的性质轻松地得到了答案，即∠1=2∠DA'E.

师：问题①和问题②存在怎样的异同呢？（教师预留充足时间让学生观察、思考）

生 6：它们都是将 △ADE 沿 DE折叠，不过点 A 的落点不同，问题①中点 A 落在四边形 BCDE 内部，而问题②落在四边形 BCDE 边上.

生7：问题①中的 ∠A' 和问题②中的 ∠DA'E 都与 ∠A 相等.

生8：图形不同，所求的结论也不同，问题①所研究的是 ∠1 + ∠2 与∠A' 之间的数量关系，而问题②研究的是 ∠1 与 ∠DA'E 的数量关系.

生9：图2中 ∠1 是 △AEA' 的外角 ， 所 以 有 ∠1=∠DA'E + ∠A ， 又∠DA'E = ∠A ，故 ∠1 = 2∠DA'E .图 1中， ∠1 和 ∠2 是四边形 A'DAE 的外角，结合四边形内角和有 2∠A' +180° - ∠1 + 180° - ∠2 = 360° ， 故∠1 + ∠2 = 2∠A' .

……

师：大家都说得非常好，若问题①也想运用三角形外角的性质来求解，可以怎么转化呢？（生积极思考）

生10：连接 AA' ，则 ∠1 ， ∠2 分别转化为 △AEA' 和 △ADA' 的外角.

师：很好，如果现在运用三角形外角的性质来探究问题①，你会吗？

结合刚刚的研究经验，学生很快给出了第二种解法.接下来，教师结合学生给出的两种解法进行点评.一种解法是之前学生采用的三角形内角和四边形内角和的解法，还有一种解法是基于问题②的探究经验，连接 AA' ，利用三角形外角的性质的解法.教师对学生的探究给予充分的肯定与表扬，学生学习积极性高涨.

师：刚刚我们研究了图 1 和图2，结合以上探究经验，你能对图3中的 ∠1 ， ∠2 提出问题吗？

在教师的鼓励下，学生积极观察、比较、讨论、交流，提出了这样一个问题：如图 3，把 △ABC 纸片沿 DE 折叠，使点 A 落在四边形BCDE 外 A' 的位置，则 ∠1 ， ∠2 与∠A' 之间存在怎么样的数量关系？说一说你的理由.（问题③）

接下来，又开启了新一轮的探究活动.教师预留充足的时间让学生思考、探究、交流，教师巡视，并对部分学生进行点拨.接下来，教师投影展示学生的探究过程，并让学生给出自己的思考过程.

生11：我与刚刚的探究思路相同，连接 AA' ，利用三角形外角的性质把 ∠1 和 ∠2 分别表示出来，然后将 ∠1和 ∠2 作差，即得 ∠1 - ∠2 = 2∠A' .

生12：令AC与A'E相交于点F，则∠1=∠A+∠AFE，∠AFE=∠A'+∠2，故∠1=∠A+∠A'+∠2，又∠A=∠A'，所以∠1=2∠A'+∠2，即∠1-∠2=2∠A'.

设计意图 在探究活动中，教师充分发挥了教师主导和学生主体的作用，通过启发与引导让学生主动将原图进行拓展，由“点 A' 在四边形BCDE 内”推广至“点 A' 在四边形BCDE 边上及在四边形 BCDE 的外部”，这样通过拓展不仅丰富了课堂教学内容，而且使探究活动更具系统性，有利于学生认知结构的优化和解题能力的提升.在以上探究活动中，教师没有急于呈现问题①的解题过程，而是借助问题②的解决，引导学生通过迁移找到了另一种解决方法，这样既提高了学生的解题信心，又让学生体会了数学知识的内在联系，有利于学生学习能力的提升.在问题①和问题②解决后，教师又让学生自主探究问题③，以此通过合作与交流，进一步升华学生的认知，提高学生的解题能力.

环节3 课堂小结

师：经历以上探究活动，你有哪些收获？有何感受？

学生积极发言，主动交流自己的所思、所获，课堂氛围活跃.

设计意图：通过小结引导学生反思回顾、总结归纳，以此进一步巩固已知知识、经验、方法.同时，通过互动交流，活跃了课堂，提高了课堂教学有效性.

环节4 拓展练习

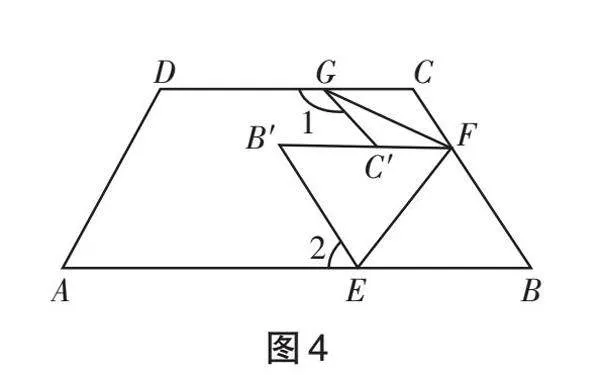
例2 如图4，把梯形 ABCD 纸片按照如下步骤折叠：①沿 EF 折叠，使点 B 落在梯形 ABCD 内部 B' 位置；②沿 FG 折叠，使点 C 落在 B'F 边的点 C'位置， B' 与 C' 位置不重合.试探究 ∠1与 ∠2 存在怎样的数量关系？请说一说你的理由.（问题④）

拓展练习可能会给一些基础较弱的学生带来一定的困扰，教师可以先让他们梳理前面的练习，在有余力的情况下继续完成拓展练习.对于基础较好的学生，教师应要求学生认真完成，完成后再帮助有困难的同学一起完成，以此通过合作让所有学生获得较大程度的提升.

设计意图 在原有例题的基础上，将题目进一步改编，以期在强化认知的基础上，发散学生的数学思维，提高学生举一反三的能力.

教学思考

1.关注学生主体价值

在提高学生解题能力的道路上，单靠教师讲授是难以达成的，应重视发挥学生的主体性，培养良好的思考习惯.在探究活动中，教师要提供机会让学生观察思考、自主探究、合作讨论、自我展示，将被动接受转化为主动获取，让学生以“主角”的身份融于课堂，激活思维，提高学生的学习品质.

2.合理引入变式训练

变式训练是提高学生解题能力的重要手段，教学中教师应合理引入变式问题，让学生在“变与不变”中体会数学的魅力，激发学生的探究欲.在以上教学活动中，教师引导学生通过“折叠”发现点 A 可以落在不同的位置，从而运用分类讨论的思想将一道题转化为三道题，使教学内容更加丰富，使学生的认知更加系统.通过变式训练，让学生感受一般到特殊再到一般的认知过程，感悟分类、转化等数学思想方法的价值，帮助学生积累了丰富的活动经验，促进了学生探究能力和创新能力的提升.

3.尊重学生个体差异

个体的差异在学习过程中是不可避免的，教师要尊重差异，对不同的学生提出不同的要求，保护学生的学习信心，激发学生的潜能，让不同层次的学生都能有所提升.在以上教学活动中，教师没有急于讲解，而是基于学生的已有认知设计探究活动，引导学生通过合作实现取长补短，充分发挥个体差异的积极作用，让每个学生都能有所发展，有所成长.

总之，在解题教学中，要摒弃单一的就题论题，为学生提供时间和机会去观察、去探索、去交流，以此帮助学生积累活动经验，提高学生的学习品质，提升学生的解题能力.