基于理性思维培养的初中数学教学策略研究

［ 摘 要 ］数学是一门要求学习者具有极强思维性的学科，想让学生学好数学就离不开对学生理性思维的培养.教学中，教师要改变传统的教学模式，为学生搭建一个自主探究和合作交流的平台，让学生经历观察、猜想、交流、归纳等过程，逐步发展理性思维，进而提高数学能力与数学素养.

［ 关键词 ］理性思维；自主探究；能力与素养

理性思维是一种思维品质，是数学学习的重要形式.数学在形成人的理性思维、科学精神和促进个人智力发展的过程中发挥着不可替代的作用.不过受唯分论的影响，部分教师的教学存在浅化、僵化、窄化等现象，“满堂灌”的课堂教学模式依然存在，学生习惯于接受，学习中常常出现“知其然而不知其所以然”的现象，影响学习效果，限制学生理性思维的发展 . 在日常教学中，教师切勿通过强灌的方式将知识教给学生，而应预留时间让学生去思考，引导学生养成追问“为什么”的品质和习惯，帮助学生厘清问题的来龙去脉，从而使学生的思维走向有序、深刻.下面，笔者结合教学实践，谈谈培养学生理性思维的几点认识.

追本溯源，执果索因

受“分数至上”价值观的影响，教学中为了追求成绩，部分教师常常直接将知识告知学生，然后布置大量的练习，以期通过“多练”加深知识理解，积累解题经验，提高解题技能 . 殊不知这样只追求“结果”的教学使得学生在解题过程中容易生搬硬套，不仅影响解题效果和解题信心，而且影响学生理性思维能力的发展.为了扭转这一局面，教师应重视引导学生追本溯源，让学生既知道知识从哪儿来，又知道知识去哪里，弄清数学知识的本源、本质，提高理性分析和解决问题的能力.

例如，在教学“全等三角形”一课时，教师启发并指导学6997cdfcb1f8fb87560a46aad514b827生通过动手操作自主探索全等条件.在研究两边和一角时，学生提出这样一个猜想：若两个三角形的两条边对应相等，且其中一条边所对的角也相等，那么这两个三角形全等.面对学生的猜想，教师没有直接评价，而是引导学生实践探究.教学片段如下：

师：请大家按照如下步骤作三角形，然后说说你的发现.（教师用PPT展示操作步骤）

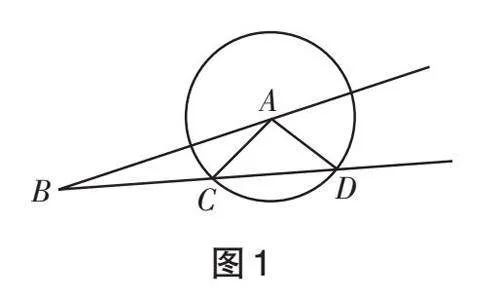
步 骤 如 下 ：（1） 画 ∠ABC ；（2） 在角的一边截取线段 AB ，在角的另一边取点 C，然后以点 A 为圆心， AC 长为半径画圆；（3） 延长BC 边，其与 ⊙A 的另一个交点为 D ，连接 AD .

学生积极操作，很快得到了图1所示的图形.

生 1： 在 △ABC 和 △ABD 中 ，AB=AB ， AC = AD ， ∠ABC=∠ABD ，这里虽然两边对应相等，且其中一边所对的角也相等，但是这两个三角形并不全等，也就是说刚刚的猜想不成立.

师：非常棒，我们在学习过程中会遇到许多神似或形似的知识内容，要加以辨析，切勿盲目套用.

师：增加一个怎样的条件，可以使刚刚的猜想成立呢？

教师鼓励学生以小组为单位，结合尺规作图的经验继续探索.学生通过操作、交流，发现若两个三角形为同一类型的三角形，那么满足以上条件的两个三角形全等.

学生通过以上探究活动，不仅激发了参与课堂的积极性，而且顺利地证明了猜想，形成了正确深刻的认识.另外，为了让学生的思维走向纵深，在此基础上，教师继续追问：增加一个怎样的条件，可以使刚刚的猜想成立？通过多角度、全方位的思考与探究，可以有效激活学生的数学思维，使学生对两个三角形全等的理解走向深刻、理性，从而在深化知识理解的同时，培养学生的理性思维，提高学生的自主探究能力.

问题驱动，思辨明理

数学是一门非常严谨的学科，在分析和解决问题的过程中要做到言之有理，论证有据.推理是理性思维的重要表现形式，其贯穿数学教学的始终.在日常教学中，教师要重视引导学生经历公式的推理过程，从而帮助学生建构一条有序的思维链条，提高学生分析和解决问题的能力.

例如，学习“多边形的内角和”时，若直接给出公式，然后套用，学生确实可以顺利地解决问题，但是没有经历自主探究的过程，学生难以形成深刻的认识，很容易遗忘.另外，公式推导过程中蕴含丰富的数学思想方法，是培养学生思维能力，发展学生理性思维的重要素材.教师应重视引导学生经历公式推导的全过程，从而在推导、讲解的过程中提高学生的综合学力.学生在学习本课内容前已经学习了三角形的内角和，并具有一定的图形分割经验.对此，教师可以学生为主，让学生通过经历从“特殊”到“一般”的探究，归纳总结出多边形的内角和.为了便于探究，教师设计了如下“任务链”，让学生在任务的驱动下，合理运用转化思想解决问题 . 任务如下：

任务 1：你想运用什么思想方法来研究？

任务 2：还可以应用哪些方法来研究？

任务给出后，学生开始独立思考，结合已有知识经验，学生最容易想到通过分割法来探索多边形的内角和.从实际反馈来看，学生大多采用分割法，但是所选取的分割方式有所不同，如有的学生从顶点出发，依次连接不相邻的顶点；有的学生在多边形内部任意找一点，连接各个点；也有学生在多边形的边上任意取一点，连接各个顶点；还有学生从多边形外部任取一点，连接各个顶点.教学中，教师先引导学生从第一种方法入手，即取多边形任意一个顶点，连接不相邻的顶点，并让学生思考以下问题：

问题 1：四边形可以分割成几个三角形？五边形可以分割成几个三角形？ n 边形呢？

问题 2：一共分割了几次？是否生成新的内角？

问 题 3： n 边 形 的 内 角 和 与（ n - 1 ） 边形的内角和有着怎样的联系？

问题4： n 边形的内角和与三角形的内角和有着怎样的联系？

学生在问题驱动下得到结论： n边形内角和为 （n - 2） × 180° .在此基础上，教师可以让学生利用其他分割方法继续探索如何推导 n 边形内角和公式，以此启发学生多角度、全方位探索问题，感悟不同方法间的关联，从而促进知识的深化 . 可见，在日常教学中，教师应坚持以学生为中心，以问题为引领，促进学生深度思考，从而培育学生的理性思维，提升学生的数学核心素养.由点及线，理性思考

学生理性思维能力是在学习过程中逐渐养成的，具有联系性、生长性.教学中，教师要引导学生从联系的视角出发，帮助学生打通从已知通往未知的思维通道，从而让学生的“学”从局部走向整体，从肤浅走向深刻，逐步提高数学应用能力，发展理性思维.例如，“数格点算面积”教学中，教师从生活实际出发，创设如下问题情境：甲、乙两人分别选取一块空地栽树，甲认为乙的土地面积大，理由是：自己地的一圈只栽15 棵树，而乙的地一圈栽了 17 棵树.而乙有不同的意见，他认为甲的面积更大，理由是：自己地的内部只能栽16棵树，而甲的地可以栽17棵树.你知道他俩谁的地面积更大？

（假设所栽树的水平、垂直间距相等）

设计意图 借助实际问题让学生体会研究不规则图形面积的重要性，有效激发学生的探究欲.

为了便于学生发现其中的规律，教师设计了如下活动：（格点多边形的面积为 S ，多边形内部的格点数为 N ，多边形边上的格点数为 L ，小正方形边长为1）

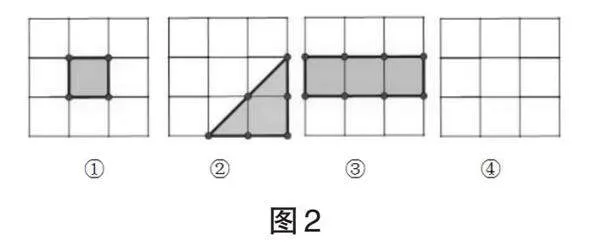
活动一：（1）如图2，其中①②③均是 N = 0 的格点多边形，请在④中再画一个 N = 0 的格点多边形.

（2）根据图2，完成表1：

（3） 结合表 1，思考 S ， L 之间的关系.

活动二：结合活动一的经验，请分别画出 N = 1 ， 2 ， 3 ，…的格点多边形，探究 S ， L ， N 三者之间的关系.

教师让学生从简单图形入手，通过操作、观察、猜想、归纳，最终得到 S ， L ， N 三者之间的关系，即 S =1/2L + N - 1 .通过由点及线的方式进行深入探索，有利于培养学生的理性思维.

总之，理性思维能力不是与生俱来的，需要通过后期的刻苦学习.在教学中，教师应致力于学生理性思维的培养，结合学生实际开展一定的探究活动，有效激活学生的理性思维，从而让学生的思维从肤浅走向深刻，有效提高学生分析和解决问题的能力，发展学生的数学核心素养.