关注主题拓展教学 实现学科育人价值

［ 摘 要 ］主题拓展教学是新课改背景下的产物，它能有效突破学生的认知边界，开阔学生的思维，发展创新意识，实现学科育人价值.研究者以“黄金分割”的教学为例，分别从“鉴赏雕塑，构建模型”“关注过程，结构创建”“实践拓展，迁移创新”三个方面展开教学设计与分析，并谈一些思考.

［ 关键词 ］主题拓展；学科育人；黄金分割

近年来，随着新课改的推进，初中数学主题拓展教学受到广大教育工作者的关注.主题拓展教学是基于某个主题，通过一系列教学活动的开展，有效帮助学生突破认知边界，提升学科的育人价值.然而，当前仍有些教师对主题拓展教学的认知不足，在主题的选择或教学活动的设计与实施上缺乏经验 . 本文以“黄金分割”的主题拓展教学为例展开阐述，与各位同行交流互鉴.

设计意图 此例是一道中考真题，教师带领学生从知识本质出发，挖掘命题背景，成功激发了学生的探索欲，提升了解题能力.与上一个环节有着异曲同工之妙的是，将问题从一维图形推广到二维，进一步开阔了学生的视野，拓宽了学生的思路.学生在此过程中，不仅获得黄金矩形的作图法，还学会了如何探寻黄金比图形结构，让学生感知黄金分割在几何图形中存在的普遍性.

活动3 实践拓展，迁移创新

要求学生结合本节课对黄金分割的理解，收集一些与黄金分割相关的作品资料，从中自主提炼数学问题，并展示交流.有兴趣的学生可在课后尝试设计与黄金比相关的logo或图片，下节课与大家分享.

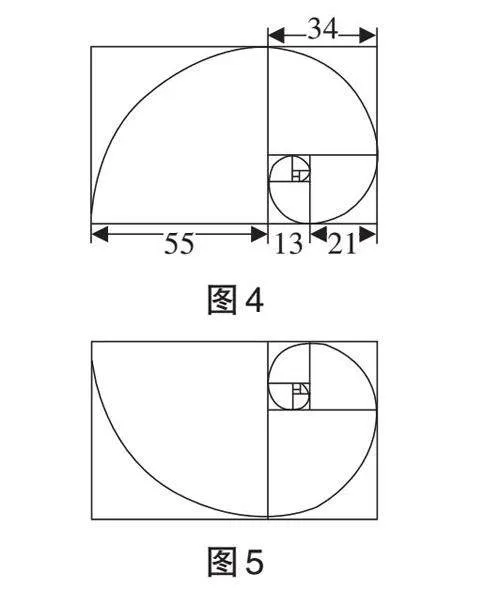
展示1：黄金螺旋线

如图4与图5，学生结合斐波那契数列获得斐波那契螺旋线，无限分割黄金矩形，获得黄金螺旋线.

也有学生将海螺、蒙娜丽莎等图片应用斐波那契螺旋线加以提炼，并一致认为自然界、美术作品、一些经典建筑等素材中均含有斐波那契螺旋线，它与黄金螺旋线为同一类螺旋线，由此充分感知黄金比确实存在于生活的方方面面.

设计意图 联系斐波那契数列与黄金矩形，将斐波那契螺旋线与黄金螺旋线之间构建连分数，有效拓展了学生的思维；学生在自主探索过程中，发现黄金分割广泛存在于各种作品、建筑与自然界中，充分感知了生活与数学之间的和谐美，由此提升了数学审美观.

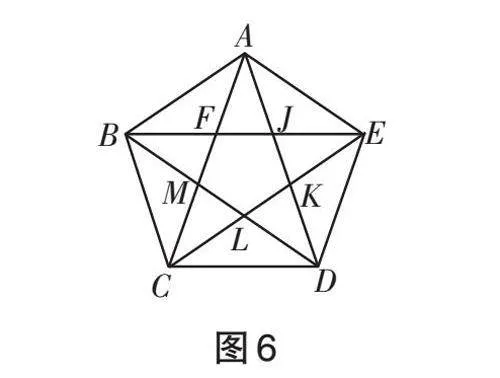
展示2 ：人马图

如图 6，将人马图抽象为正五边形，其中蕴含了大量的黄金比例.

问题3 结合我们的研究经验，说说可用什么办法来研究正五边形.

师生活动：研究某个几何对象，首先要研究它的基本要素、要素之间、要素与其他相关要素间的联系.那么研究正五边形则可从边、角、线段等要素着手，通过探索要素间的关系获得一些发现.（研究过程略）

设计意图 人马图抽象为正五边形的研究，意在引导学生从中发现黄金比的广泛存在，促使学生学会进行研究方法的迁移与思维的创新.

几点思考

1.选好拓展主题，开阔学生视野

主题拓展教学的目的是发散学生的思维，让学生在教学活动的开展中挖掘潜能，拓宽视野，形成创新意识 . 因此，选择什么内容作为拓展的主题非常重要，它决定了教学的成败 . 实践证明，符合学生学习经验与认知水平的主题，往往能快速吸引学生的注意，让学生积极地投入课堂探索中来 . 值得注意的是，教师所选择的主题必须与课标要求相契合，既高于学生现有的认知水平，又要满足教材教学要求.

本节课，教师结合学生实际情况，选择了“黄金分割”作为拓展主题，符合学生的认知与素养发展需求.该主题本身就具有深厚的文化底蕴与艺术气息，学生一起探索充满数学美的黄金分割，不仅能进一步夯实知识基础，还能对黄金分割的来龙去脉产生深刻理解.因此，该主题对发展学生个人的审美观具有重要价值与意义.

2.设计拓展活动，发展创新意识

新课改背景下的数学课堂是以学生为主体的课堂，教师应为学生提供大量的活动机会，让学生有机会在活动中开阔思维，进行知识与研究方法的迁移，发展创新意识.如本节课的人马图到正五边形的抽象思维，就为学生提供了一次良好的活动机会，让学生通过对正五边形与黄金分割的深入探索，创新研究方法.

3.以拓展为基点，发展理性精神

主题拓展教学，顾名思义就是在某个特定主题的基础上，进行探索与研究.拓展的深入，可深化学生对“主题”的理解，而拓展的探索与研究过程对学生的数学思维与推理能力提出了较高的要求.关注探索过程，一方面能有效激发学生的研究兴趣，另一方面能发展学生的数学理性精神.

本节课，虽然研究的主题是“黄金分割”，但学生接触到的内容却非常广泛，如维纳斯雕像、斐波那契数列、人马图等.这些内容从真正意义上拓宽了学生的视野，让学生学会用数学的眼光、思维与语言来领悟这个世界.随着每一项内容的深入探索，学生通过猜想、运算、分析等环节，逐渐形成良好的推理能力，获得数学理性精神，突出了主题拓展教学的育人价值.

总之，生活中存在大量“美”的事物，如建筑、人文、艺术等，都含有丰富的黄金之美 . 如果我们仅仅单纯地用肉眼去观察，只能带来一定的视觉冲击，无法从真正意义上感受它的内涵，更谈不上育人价值 . 从数学的角度来审视这些“美”，则让“美”变得更加富有内涵 . 因此，将理性之美与自然之美深度融合，是塑造良好人格品质的基础.