基于深度模糊学习的牙科CBCT运动伪影校正算法

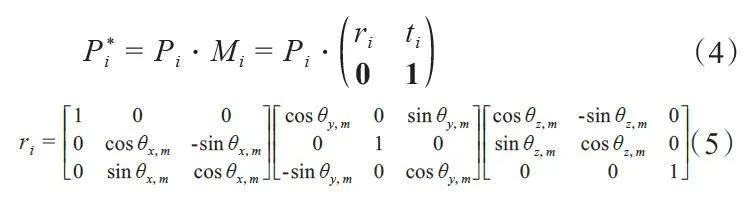
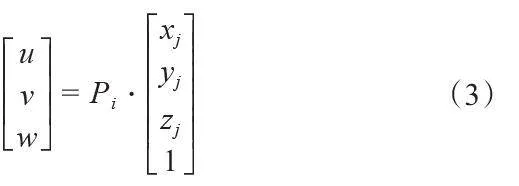
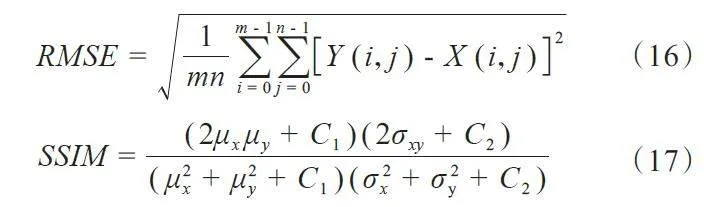
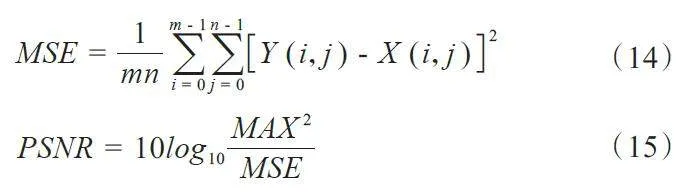
摘要：目的 针对牙科CBCT 扫描中患者不自主运动导致的重建图像运动伪影问题，提出了一种基于深度模糊学习的牙科CBCT运动伪影校正算法（DMBL），以提升牙科CBCT的成像质量。方法 首先使用模糊编码模块提取运动退化特征，从而对运动导致的退化过程进行建模，然后将得到的运动退化特征输入伪影校正模块进行运动伪影去除。其中，伪影校正模块采用了图像模糊去除和图像模糊仿真的联合学习框架，可有效处理空间变化且随机的运动模式。为验证所提方法的有效性，本文分别在仿真运动数据集和临床数据集上进行对比实验。结果 仿真数据集实验结果表明，本文方法峰值信噪比提升了2.88%，结构相似性（SSIM）提升了0.89%，均方根误差（RMSE）减少了10.58%；临床数据集实验结果表明，本文方法取得了最高的专家主观图像质量评分4.417（5 分制），且与对比方法结果的评分具有显著性差异（Plt;0.001）。结论 本文提出的DMBL算法，通过构建深度模糊联合学习网络结构，能够有效地去除牙科CBCT图像中的运动伪影，实现高质量的图像恢复。

关键词：运动伪影校正；牙科CBCT；模糊学习

牙科CBCT相较于传统CT具有空间分辨率高、成像质量好等优点，可为口腔种植、正畸、修复等口腔治疗提供可靠的三维可视化影像［1］。然而，牙科CBCT由于扫描速度较慢（5.4～40 s）［2］，增加了扫描过程中患者发生不自主运动的概率。有研究表明，21%～41%的患者在扫描过程中存在不自主运动［3］。扫描过程中患者的不自主运动会导致投影数据不一致，在重建图像中出现条纹伪影，组织轮廓重叠及结构模糊等问题，引起图像质量退化，对临床诊断和治疗产生不利影响。特别当患者不自主运动幅度较大时，往往需要多次扫描以获取满足诊断需求的影像，这不可避免地增加了患者遭受的X射线辐射剂量。尽管在实际中牙科CBCT扫描采用了牙托等硬件装置对患者进行固定，但该措施不能完全消除头部运动［4］，而一些轻微的运动（gt;3 mm）就会对图像质量产生明显影响［5］。为获取能够满足临床诊断的高质量图像，国内外学者先后提出了许多针对运动伪影的软硬件校正算法，主要分为运动标记方法、运动补偿方法和深度学习方法3类。

第1类运动标记方法通过添加外部光学运动跟踪设备和基准标记来获取患者的运动轨迹，用于投影数据的一致性校正，实现运动伪影去除［6-9］。例如，Kim等［8］使用光学运动跟踪系统同时记录床和被扫描模体的运动，并用于恢复投影一致性以进行运动补偿校正。然而，这类方法需要的硬件较为昂贵，增加了设备额外的成本，并且牙科CBCT扫描室内部空间有限，难以将此类光学硬件集成到现有机器中。第2 类运动补偿方法通过校正算法估计患者的运动轨迹信息，并利用该运动轨迹对投影进行运动补偿，以重建无伪影的图像，主要包括基于自校准方法［10-13］、基于一致性条件的方法［14， 15］及3D-2D配准方法［16， 17］。例如，Sisniega等［10］提出一种基于图像的运动补偿方法，采用CMA-ES算法估计运动轨迹并进行运动补偿；Preuhs等［15］提出一种基于极线一致性的方法，从投影图像估计对称平面，并引入X轨迹利用对称性来估计运动；Ouadah等［16］提出了一种基于3D-2D图像配准的运动伪影校正方法，通过使用CMA-ES优化器最大化梯度来进行投影-图像配准，并将得到的刚性运动变换参数用于运动补偿重建。然而这类方法需要对投影进行多次重建直至收敛，计算复杂、运算量较大，较为耗时，且运动补偿效果受运动估计精度的影响很大。第3类深度学习方法能够直接学习图像中的运动伪影表征，具有良好的运动伪影去除性能，同时不需要多次迭代重建，相比于传统方法具有更高的计算效率，更适用于牙科CBCT的运动校正任务。例如，Hu等［18］提出基于WGAN的单幅图像运动伪影抑制方法，能够有效地去除牙科CBCT图像中的运动伪影；Su等［19］提出一种消除CT头部运动伪影的多尺度卷积神经网络，从无运动图像模拟运动伪影并用于网络训练；Ko等［20］提出一种基于自注意力机制的深度卷积神经网络框架，用于补偿CT运动伪影，该方法能够成功地处理各种运动场景。然而，现有网络方法只考虑到二维平面内的运动，而没有考虑三维平面的运动，在实际临床扫描中，三维CBCT图像中存在若干张连续的伪影切片，且这些切片在空间上存在连续的组织结构，现有网络很难处理这种伪影。同时，由于配对数据之间存在像素偏移，导致网络输出图像在高频区域出现细节损失，降低图像诊断质量。

针对上述问题，本文提出一种基于深度模糊学习的运动伪影校正网络（DMBL），由模糊编码模块和伪影校正模块组成，其中模糊编码模块对伪影图像中的运动信息进行编码以提取空间变化的多尺度运动特征，指导伪影编码模块完成图像恢复任务。伪影校正模块采用一种图像模糊去除和图像模糊仿真的联合学习框架，以提高所提取运动特征的泛化性；对于配对数据之间存在像素偏移导致图像分辨率损失的问题，本文引入上下文损失，以保持牙齿和骨小梁等高频区域的细节。在仿真和临床数据集上进行了实验，实验结果表明本文方法具有良好的运动伪影校正性能。

1 资料和方法

1.1 牙科CBCT运动伪影仿真

在实际临床实践中，获取真实配对数据，包括有运动伪影和无运动伪影的图像，常常存在困难。因此在网络训练过程中，通常会采用仿真的方法来生成配对运动伪影数据，以便用于网络的训练。目前运动伪影仿真算法主要有两种：（1）使用外部装置（如机器臂）在扫描过程中移动体模来仿真运动［21］，但是这类方法能够仿真的运动形式有限。（2）数字仿真方法，在前投影过程中加入运动轨迹来获取运动数据［22］，但该方法采用的重建体数据已经存在信息丢失，直接对其前投影得到的仿真投影数据和真实数据存在不一致。因此，本文提出一种新的数字仿真方法，首先利用CBCT几何信息构建投影几何矩阵，然后采用随机运动矩阵对投影几何矩阵进行调制，以此在重建过程中增加运动信息，再利用修改后的投影矩阵进行重建得到仿真运动数据。这类方法得到的仿真图像更接近于真实的运动图像，且不存在数据截断等问题。

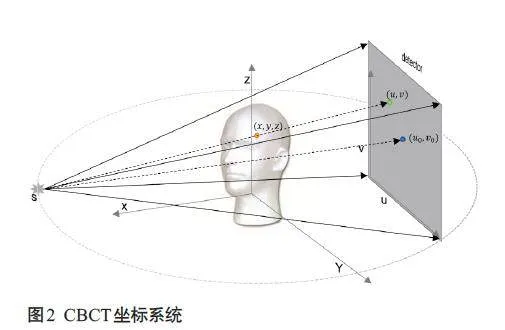
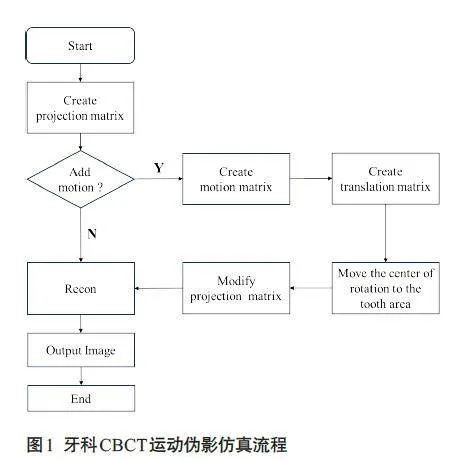
本文采用的运动仿真流程如下（图1），基于CBCT几何构建投影矩阵，围绕旋转中心建立世界坐标系（ x，y，z ），以及探测器平面坐标系（u，v ），其中射源S 和探测器围绕Z轴旋转（图2）。

对于CBCT，其重建所需的几何信息可以按投影角度参数化为一个大小为3×4 的投影矩阵［23］，即Pi ∈ R3 × 4，其中i = 1，...，N，N为扫描采集的投影个数。每个角度的投影矩阵Pi可分解为内参矩阵K ∈ R3 × 3 和外参矩阵Ei ∈ R3 × 4，其中Ei包含旋转矩阵Ri ∈ R3 × 3以及平移向量Ti ∈ R3 × 1，即：

Pi = KEi = K [ Ri|Ti ] （1）

对于单个角度，扫描物体中单个标记点的投影变换可以表示为：

Yj = Pi （ Xj ） （2）

其中，Xj = （ xj，yj，zj，1） 为齐次坐标， Yj = （u，v，w ） 为对应投影点坐标，Pi为第i个角度下的投影矩阵，公式2可转写为如下形式：

在CBCT坐标系统中，头部刚性运动包括6个自由度，定义为S = [ tx，m，ty，m，tz，m，θx，m，θy，m，θz，m ]，其中（ tx，m，ty，m，tz，m ） 为沿X，Y，Z 轴的平移分量，（ θx，m，θy，m，θz，m ）分别为绕三个旋转轴的旋转角度。设物体在投影角度i下的运动矩阵Mi ∈ R4 × 4，受运动影响的投影矩阵可以表示为以下形式：

其中，每个Mi由三维旋转矩阵ri （ θx，m，θy，m，θz，m ）和平移向量ti （ tx，m，ty，m，tz，m ）组成。对于每个投影角度，通过将患者的运动合并到投影矩阵Pi，得到修改后的P*i 进行重建，可以在重建图像中产生运动伪影。同时本文将仿真得到的数据与真实数据进行比较，以证明本文方法的可靠性。

1.2 基于模糊编码的运动校正模型

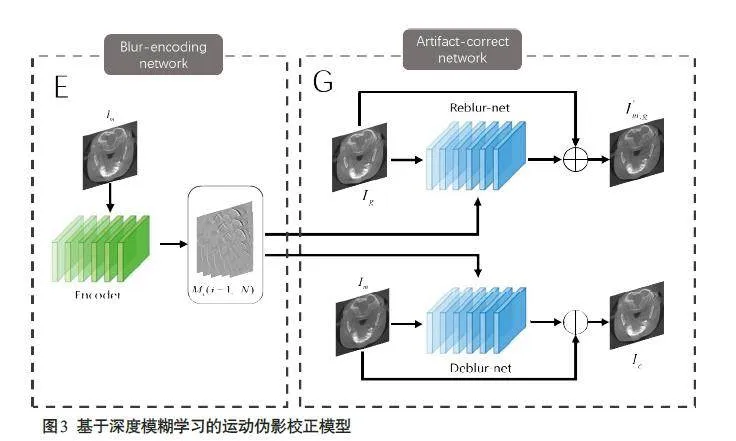
本文提出的基于深度模糊学习的运动伪影校正（DMBL）网络模型如图3所示，网络包含模糊编码模块E和伪影校正模块G两部分，模糊编码模块E的作用是学习运动伪影图像中的退化特征，并将学习到的特征输入到后续网络用于指导运动校正任务，伪影校正模块G采用联合学习框架，利用学习到的多尺度运动退化特征对输入图像进行运动伪影校正。

伪影校正模块中，图像模糊仿真网络以无运动伪影图像作为输入，根据提取到的退化特征生成运动伪影图像，图像模糊去除网络以运动伪影图像作为输入，并利用学习到的退化特征在不同尺度下对输入运动图像的特征进行调制，实现运动伪影校正。通过这种联合图像模糊去除和图像模糊仿真的框架来学习运动伪影的显式退化表示，能够提升网络学习退化表征的能力，使网络可以很好地处理空间变化且复杂的模糊过程（图3）。

1.2.1 模糊编码模块

当前基于深度学习的运动伪影校正方法未对引起图像模糊的运动过程进行建模，因此难以处理空间变化的复杂运动模式，如三维CBCT图像中存在的连续多层伪影切片。为此，本文考虑对运动导致的退化过程进行建模，从而更好地处理空间变化的复杂运动信息。

具体地，对运动导致的退化图像进行建模，理想投影可以视为扫描物体经过前投影再加上噪声的结果，即：

y = Px + ε （7）

被扫描物体发生运动时，运动投影相当于物体在前投影之前先经过一个运动退化过程，即：

y = P （ x ⋅ k ） + ε （8）

其中k表示运动退化过程，在运动伪影校正任务中，k包含扫描过程中物体的运动信息。对k 的建模有两种方式：一是将k 建模为模糊核，这种方法的缺点是假设的模糊核往往是线性和均匀的，并不适用于现实中非均匀且空间变化的运动过程，因此可能会在图像中引入额外的伪影。二是将k建模为显示退化特征，这种方式能够处理复杂的退化模式，更适用于CBCT运动伪影校正任务。为此，本文中的模糊编码模块采用卷积神经网络作为编码器，从输入CBCT运动图像中提取运动相关的显示退化特征，再利用该退化特征指导后续校正网络进行运动伪影去除。

1.2.2 伪影校正模块

研究表明，联合图像去模糊和再模糊的学习框架在自然图像去模糊任务中取得了较好性能［24］，受此启发，本文将该联合学习框架引入到伪影校正模块，搭建图像伪影仿真——伪影校正网络，通过这种联合学习策略使模糊编码器更好地学习运动导致的退化特征，提高模型性能。

伪影校正模块包含两部分：图像模糊仿真网络Greblur和图像模糊去除网络Gdeblur，网络采用生成-对抗结构，生成器部分由Restormer网络进行扩展。同时，为了利用编码器提取到的运动信息，采用空间自适应调制模块［25］将运动退化特征集成到两个网络中。图像模糊仿真网络Greblur以无伪影CBCT图像作为输入，借助模糊编码器提取到的运动退化特征，从无伪影图像中生成伪影图像，以此来模拟运动退化过程。Greblur采用残差学习的方式，仅学习无伪影图像和伪影图像之间的残差，这样的策略能使模糊编码器专注于提取与内容无关的运动相关特征，从而提高模糊编码器的编码性能。图像模糊去除网络Gdeblur以运动模糊图像作为输入，在不同尺度下利用提取到的运动退化特征对网络低维特征进行调制，调制后的特征能够帮助网络更好地处理各种复杂的运动模式，实现更好的校正性能。

1.2.3 网络结构

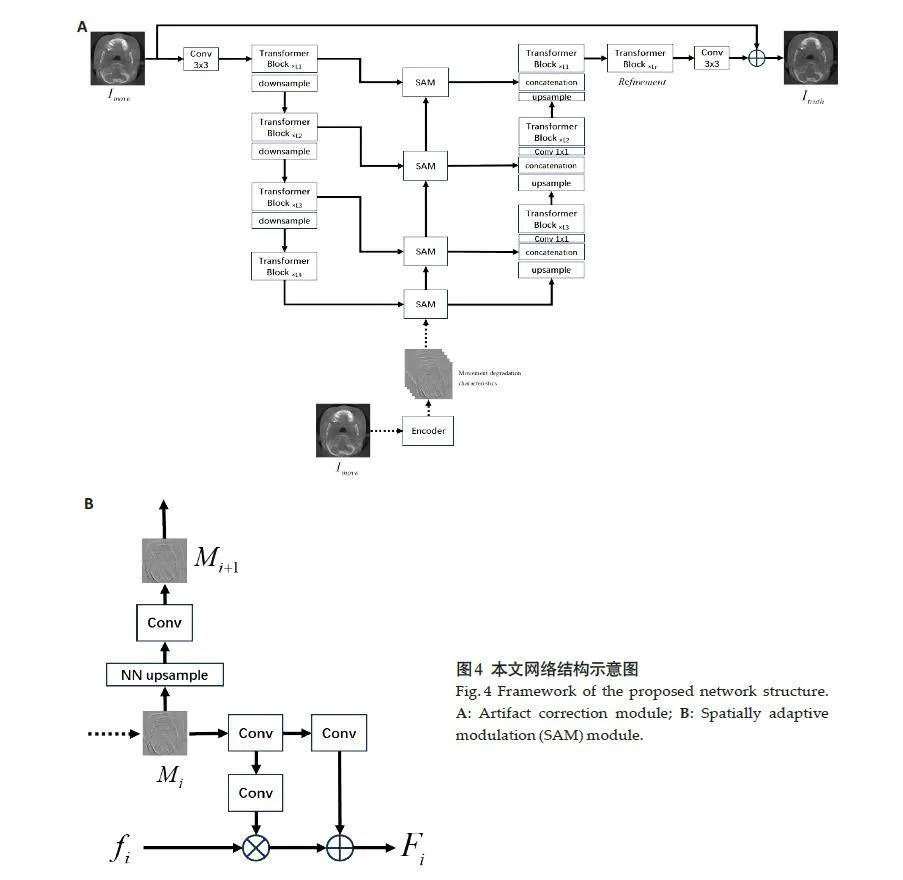
图4A为伪影校正模块采用的网络结构。网络首先使用一个3×3的卷积层来提取输入图像的基础特征，然后通过4层对称的编码-解码结构得到图像的高维特征，每一层编码/解码器均包含多个Transformer模块，随着层数的增加模块数量逐渐递增，分辨率逐渐递减。编码器和解码器之间通过跳跃连接来传递低维特征信息，并通过空间自适应调制模块将模糊编码器学习到的运动退化特征集成到网络中，在不同尺度下对跳跃连接中的特征进行调制。接着，将输出的高维特征fd输入到Refinement模块进行细化，最后将细化后的特征经过一个3×3的卷积层，并与输入图像相加得到校正后的图像。

图4B为空间自适应调制模块，其作用是将提取到的退化表示集成到网络的跳跃连接中。如图所示，首先将编码器提取到的尺度为i的运动特征Mi通过卷积层得到缩放参数γi和偏置参数βi，然后根据调制参数对第i层的跳跃连接特征fi进行调制得到Fi：

Fi = γi ⋅ fi + βi （9）

接着，将Mi进行上采样和卷积得到尺度为i + 1时的退化特征Mi + 1，用于下个尺度的特征调制。退化特征的输入能够加强模糊编码器与伪影校正网络之间的联系，使模糊编码器能够更好地学习运动相关的退化特征，提高特征的表示能力，从而使网络能够处理各种复杂的运动退化模式。

1.2.4 损失函数

假设x为输入伪影图像，x′为网络生成的伪影图像，y为无伪影标签图像，y′为网络校正后的无伪影图像。对于图像模糊仿真网络，采用感知损失和对抗损失来帮助网络对运动模糊过程进行建模，其中对抗损失采用hinge损失，图像模糊仿真网络的目标函数表示如下：

LG = -Ey～pdataD（ x′，y ） + λ1 Lperceptual （ x，x′ ） （10）

LD = -E（ x，y ）～pdata[ min （0，-1 + D（ x，y ） ） ] -Ey～pdata [ min （0，-1 - D（ x′，y ） ） ] （11）

其中D为条件模糊判别器，Lperceptual为感知损失，λ1是平衡判别器损失和感知损失的权重。

对于图像模糊去除网络，为避免校正图像中出现分辨率降低、细节损失等情况，在目标函数中引入 L1范数损失和上下文损失［26］，用以衡量伪影校正模块输出图像与真实无伪影图像之间的差异，同时保留更多的图像细节。图像模糊去除网络的目标函数表示如下：

Ldeblur = L1 （ y，y′ ） + Lcontext （ y，y′，l ） （12）

其中上下文损失

Lcontext （ y，y′，l ） = -log （CX （ φl （ y ），φl （ y′ ） ） ） （13）

其中CX 为上下文相似度，φ 为VGG19 预训练网络，φl （ y ）、φl （ y′ ）分别为第l层VGG19网络从图像y和y′中提取的特征。

1.3 实验设计

1.3.1 实验数据

由于配对的运动数据获取较为困难，本研究使用商用牙科CBCT（Fussen Matrix5000）数据集进行仿真和训练。数据集共包含18例无运动伪影真实病人数据，每例数据包含500 张切片，每张切片大小为800×800，分辨率为0.2mm×0.2 mm×0.2 mm。使用本文提出的仿真方法对每例数据采用10组不同的运动参数进行仿真，最终得到180套含不同程度运动伪影的配对数据集{ I kmove，I ktruth }（ k = 1，...，180 ），将其中150 套作为训练集，30套作为测试集，分别用于模型训练和测试。此外，从牙科CBCT数据集中选取2套不同程度的运动数据作为真实数据进行测试。

1.3.2 对比方法和评价指标

本文通过仿真运动伪影数据和真实临床运动伪影数据验证本文算法性能，并选取4 种不同网络作为本文的对比方法，分别为U-Net［27］、WGAN［28］、HINet［29］、Restormer［30］。对于仿真数据结果，本文采用三种评价指标进行定量分析，分别为峰值信噪比（PSNR），均方根误差（RMSE）和结构相似性（SSIM），各评价指标的计算公式如下：

其中Y为无运动标签图像（真值），X表示不同网络输出的校正图像。MAX为真值图像中的最大像素值。

其中μx，μy，σx，σy和σxy分别表示校正图像X和真值图像Y的均值、标准差和互协方差。

对于临床数据结果，由于缺乏真值图像作为参考，因此本文首先根据图像的视觉效果进行评价，再由6名临床影像专家对临床数据结果进行评分（5分制）。根据6名专家的临床影像经验，将评分分为5个等级。5分：图像中无伪影，结构恢复较好；4分：图像良好无明显条纹，只在牙齿区域附近有少量模糊；3分：图像中存在少量条纹伪影，牙齿和骨组织存在模糊；2分：图像中有显著条纹，牙齿和周围组织模糊不清；1分：图像中有严重的运动伪影，牙齿结构剧烈失真。评分结果以“均数±标准差”表示，并采用曼-惠特尼U检验以验证本文方法与对比方法之间的去伪影性能是否有显著差异，Plt;0.05表示差异具有统计学意义。

同时，为验证联合学习框架对加强网络运动伪影去除性能的有效性，实验设计了单一Restormer网络模型与联合学习框架模型进行对比试验。两种模型均采用仿真运动伪影数据作为输入。

2 结果

2.1 运动伪影仿真结果

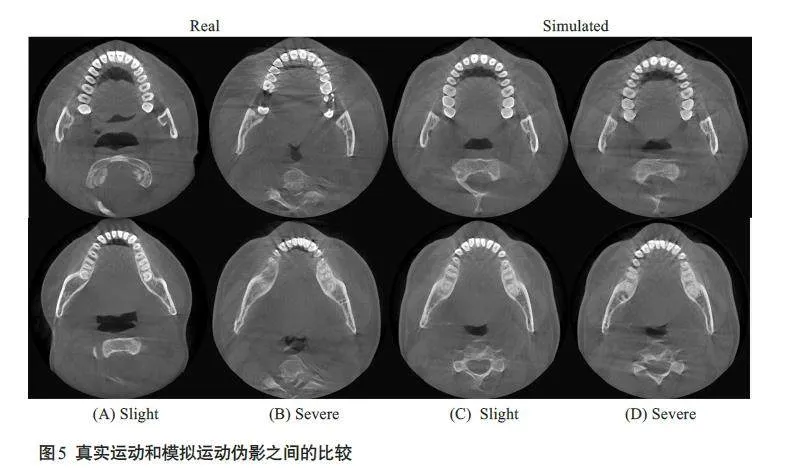
图5显示了受运动影响的真实数据与本文提出的数字仿真方法模拟得到的数据之间的比较结果，其中（A）、（B）列为真实运动数据，（C）、（D）列为仿真运动数据。对于仿真运动数据，（C）列和（D）列分别表示同一人体部位发生轻微运动和剧烈运动的图像对比结果。

2.2 仿真数据实验结果

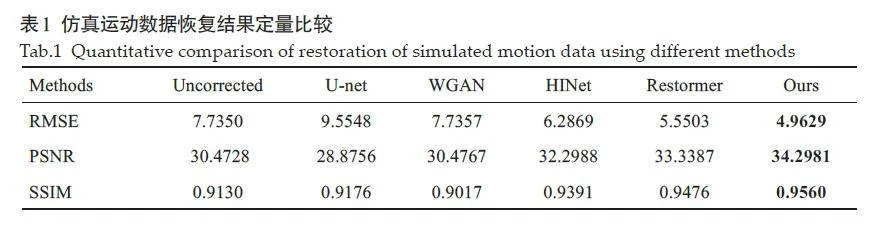
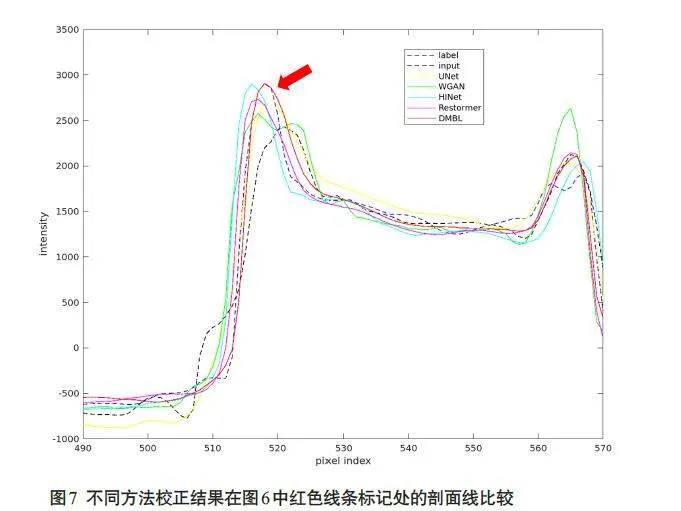
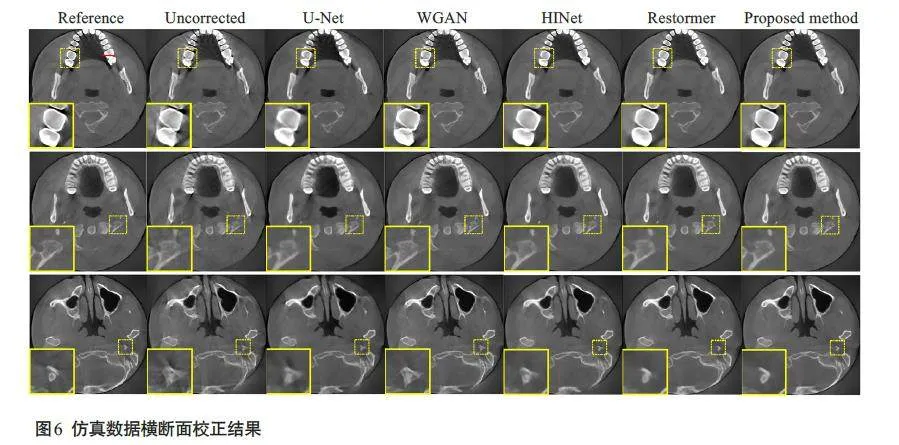
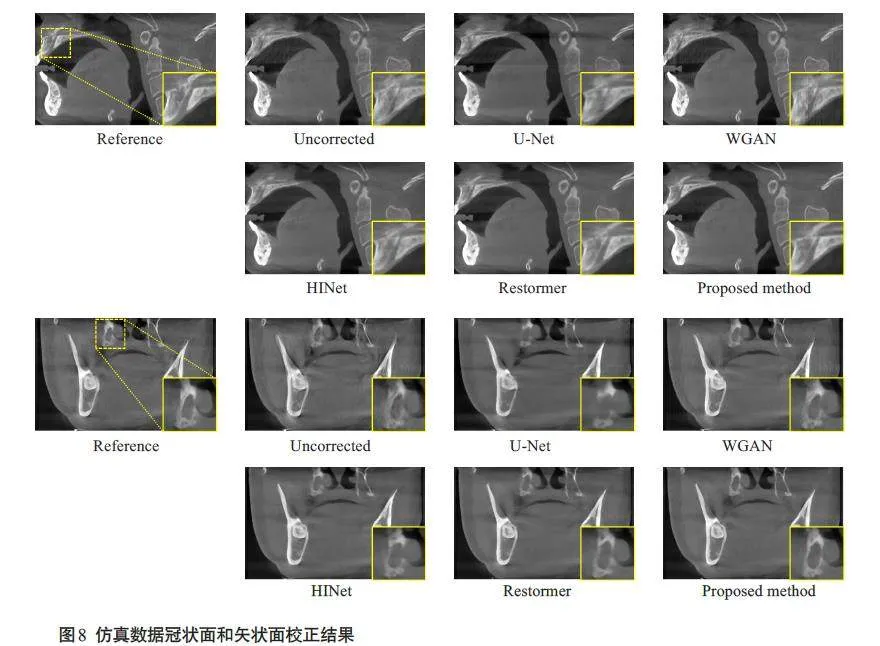
图6 显示了仿真运动数据的横断面校正结果，Reference 和Uncorrected 分别表示无运动图像和受运动伪影干扰的失真图像，其余为不同方法恢复后的校正图像。图像显示窗宽均为3000，窗位均为400。图中左下角的黄色方框内为图像的局部细节放大图。从结果可以看出，本文所提出的方法在运动伪影抑制和组织结构保持等方面的表现优于其他对比方法，对牙齿和骨组织区域的细节恢复较好。图7显示了图6校正网络结果中红色线条标记位置的水平剖面线。与对比方法相比，本文方法恢复后的图像剖面线更接近于参考图像。图8显示了仿真运动数据的冠状面和矢状面校正结果，由图可知，相较于对比方法，本文所提出的方法能够很好地处理图像中层与层之间的运动伪影，同时恢复骨组织的结构信息。表1 为仿真运动数据不同方法校正结果的PSNR、SSIM和RMSE指标。与对比方法相比，本文算法取得了最高的PSNR指标（34.2981），最高的SSIM指标（0.9560）以及最低的RMSE指标（4.9629）。

2.3 临床数据实验结果

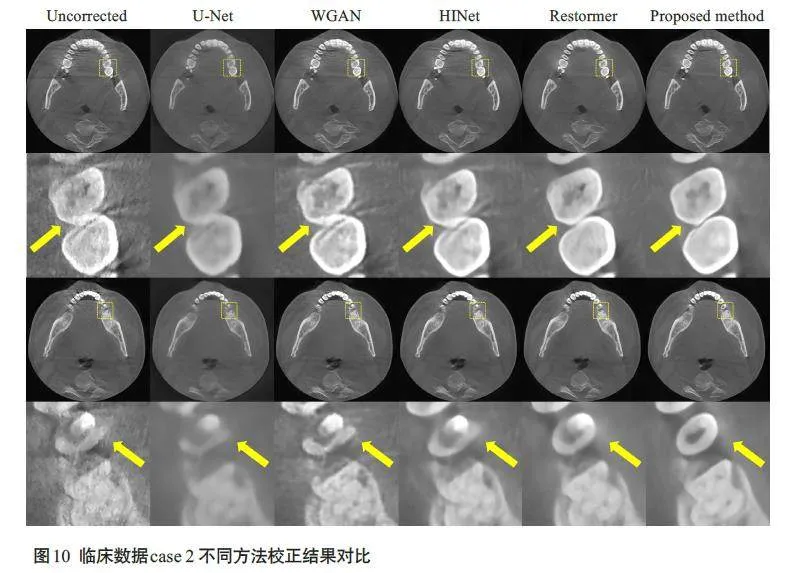
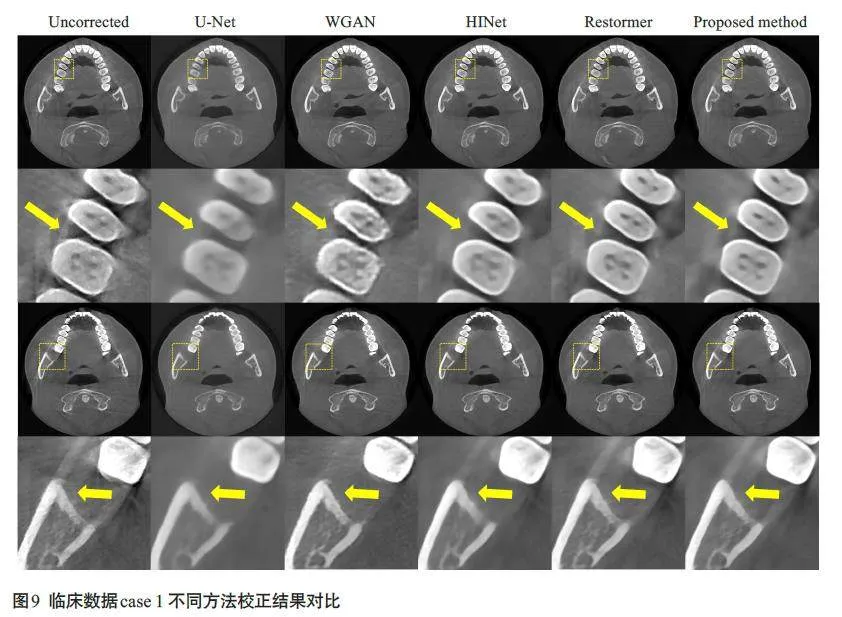
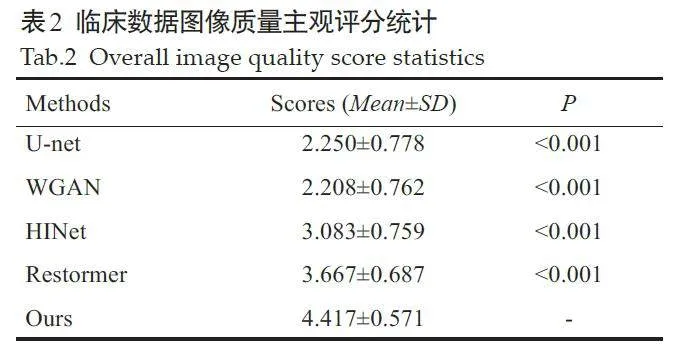
为进一步验证本文方法的有效性和鲁棒性，本文选取2 例具有不同运动程度的牙科CBCT临床数据进行验证，图像显示窗宽均为3000，窗位均为400。图9显示了不同校正方法对第1例临床数据的处理结果。第1例临床数据含有轻微运动，在图像中表现为条纹伪影，牙齿结构模糊以及骨组织出现双边缘。从结果中可以看到，本文方法对组织结构保持得较好，并在一定程度上抑制了牙齿和骨组织周围的运动伪影。第2 例临床数据含有较为剧烈的运动，图像中包含更严重的条纹伪影，同时牙齿和骨组织轮廓不清晰（图10）。与对比方法相比，本文方法结果消除了图像中的运动伪影，同时很好地恢复牙齿和骨组织轮廓。表2 显示了不同校正方法对临床数据恢复结果的图像质量主观评分统计情况。其中本文提出的算法在临床数据结果中获得的评分最高（4.417±0.571），从U检验结果中可以看到，本文算法与其他4 种对比方法的图像质量评分具有显著性差异（Plt;0.001）。

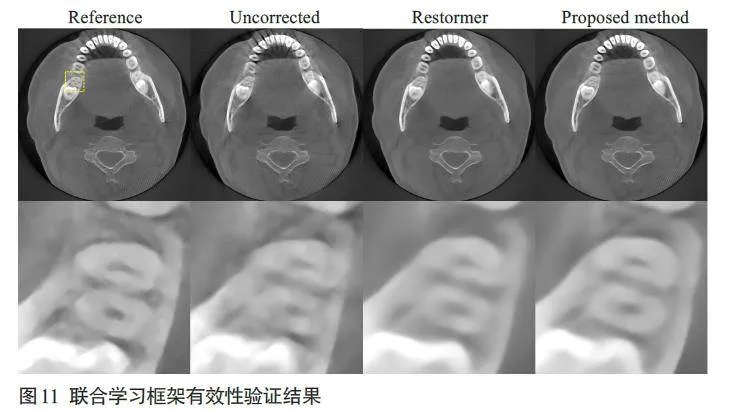
2.4 联合学习框架有效性验证结果

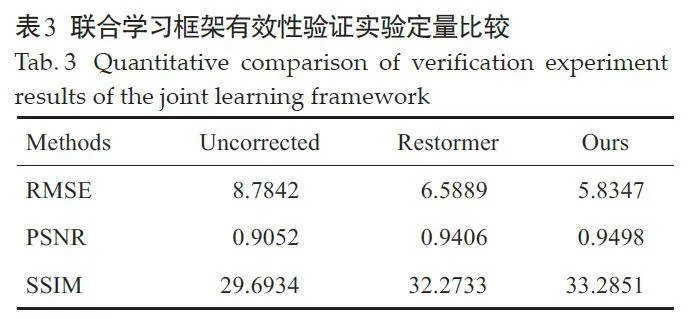
图11 显示了对联合学习框架有效性验证实验中，单一Restormer模型和联合学习框架模型的伪影校正结果。验证结果表示，联合学习框架模型结果能够很好地去除牙齿周围的结构模糊，对牙齿组织结构的恢复效果也较好。表3为图11所示图像的定量评价指标，结果显示联合学习框架模型在PSNR、SSIM和RMSE的指标上均优于单一Restormer模型。

3 讨论

为解决牙科CBCT扫描中患者不自主运动导致的重建图像运动伪影问题，本文提出了一种基于深度模糊学习的牙科CBCT运动伪影校正算法（DMBL），对运动导致的退化过程进行建模。具体地，本文首先通过模糊编码器提取运动相关的退化特征，然后将运动退化特征输入到伪影校正模块进行伪影去除。其中，伪影校正模块采用图像模糊去除和图像模糊仿真的联合学习框架［24］，以加强模糊编码器提取运动特征的性能，使网络能够处理空间变化且复杂的运动模式，提升模型的伪影校正性能。

本文采用牙科CBCT仿真运动数据集和临床运动数据集进行评估。从仿真数据和临床数据的校正结果可以观察到，U-Net 结果中出现图像过模糊，这是由于运动图像与真值图像之间存在像素不匹配，仅采用像素级损失会导致图像损失高频信息［32］。WGAN结果能够去除牙齿周围的条状伪影，但是会在牙齿附近引入新的伪影，其原因可能是在网络训练过程中，网络将图像中牙齿区域的伪影特征当成牙齿特征进行学习［18］。HINet［29］和Restormer［30］结果可以去除图像中的大部分条纹伪影和牙齿组织周围的边缘模糊，但丢失了一些牙齿边缘细节和骨组织结构，同时仍有部分牙齿存在结构失真，如牙齿边缘未闭合。与上述方法相比，本文提出的DMBL模型可以更有效地抑制图像中存在的运动条纹伪影，以及牙齿和骨组织区域的边缘模糊，同时能够更好地保持高频区域如牙齿和骨组织的结构细节。同时，本文所提模型对于图像中层与层之间的运动伪影也有较好的校正效果，能够去除骨组织的层间混叠及条纹伪影，同时恢复结构信息。这些结果说明本文采用的模糊学习策略，可以有效地提取图像中的运动退化特征，使运动校正模型能够更好地处理运动导致的伪影。在定量评估结果中，本文所提方法取得了最高的PSNR指标，最高的SSIM指标和最低的RMSE指标，充分证实了本文所提方法可以更好地去除牙科CBCT 图像中的运动伪影，同时保留更多的细节和组织结构信息。

在联合学习框架有效性验证实验中，通过图像分析和定量分析结果可以看出引入联合学习框架可以加强模糊编码模块提取运动特征的性能，从而有效地指导运动伪影去除任务，提高运动校正网络去除运动伪影的性能。实验验证了联合学习框架的有效性。

在数据仿真方面，现有运动仿真方法通过在前投影过程中加入运动轨迹来获取运动数据［19］，但是这类方法得到的仿真投影数据和真实数据存在不一致，从而降低配对数据的质量，影响网络训练。为此，本文提出一种基于投影几何矩阵的运动仿真方法，采用随机运动矩阵对CBCT投影几何矩阵进行运动调制，并在重建过程中引入运动信息。本方法获得的仿真运动数据与真实数据有着近似的图像伪影表征，同时能够避免前投影仿真方法中存在的数据不一致问题，提供优质的配对运动数据用于网络训练。

在损失函数方面，由于CBCT存在三维运动，考虑到运动配对数据之间会存在像素的偏移，从而导致网络处理结果中出现图像分辨率损失，本研究引入上下文损失［26］对图像高频区域进行约束，以保持牙齿和骨小梁等高频区域的细节。

本文方法的优势在于：牙科CBCT扫描中的刚性运动发生在三维空间，其运动模式较为复杂，产生的伪影表征与组织区域和运动剧烈程度有关，包含空间变化的运动信息，现有运动校正网络很难处理这类复杂伪影［31］，本文提出的DMBL模型采用模糊编码器对运动退化过程进行建模，以提取空间变化的运动特征，同时引入一种联合学习框架增强模糊编码器提取特征的能力，使得模型能够处理各种复杂的运动伪影；引入上下文损失，以保持牙科CBCT图像中牙齿和骨小梁等高频区域的细节纹理；与现有仿真方法相比，本文采用基于投影几何矩阵的运动仿真方法，能够避免现有方法中存在的数据不一致问题，获取优质的运动配对数据用于网络训练。

本研究存在一定的不足和发展空间：本文实验所用的患者数据有限，而现实中的患者运动存在更复杂的情形，例如患者牙齿部分存在金属时，重建图像中金属伪影的存在会让运动伪影的表征变得更加复杂，下一步工作将针对此类数据进行扩充，将本文方法拓展到含有金属的运动场景；虽然仿真所用的随机运动矩阵能涵盖一定运动模式，仿真得到的运动伪影也接近临床真实数据，但仍有部分运动模式没有被覆盖，未来的工作将结合实际扫描过程中患者的运动情形对运动矩阵加以约束，得到更优质的运动配对数据用于网络训练。

综上所述，本文算法采用图像模糊去除和图像模糊仿真的联合学习框架，提高模糊编码器的运动特征提取能力，使得网络能够处理复杂的运动模式，从而更有效地抑制运动伪影，同时保留更多的结构信息。本文算法可以有效去除牙科CBCT图像中的运动伪影，实现高质量图像恢复，具有良好的临床应用潜力。

参考文献：

[1] Kaasalainen T， Ekholm M， Siiskonen T， et al. Dental cone beam CT：an updated review[J]. Phys Med， 2021， 88： 193-217.

[2] Nemtoi A， Czink C， Haba D， et al. Cone beam CT： a currentoverview of devices[J]. Dentomaxillofac Radiol， 2013， 42（8）：20120443.

[3] Spin-Neto R， Wenzel A. Patient movement and motion artefacts incone beam computed tomography of the dentomaxillofacial region：a systematic literature review[J]. Oral Surg Oral Med Oral PatholOral Radiol， 2016， 121（4）： 425-33.

[4] Hanzelka T， Dusek J， Ocasek F， et al. Movement of the patient andthe cone beam computed tomography scanner： objectives andpossible solutions[J]. Oral Surg Oral Med Oral Pathol Oral Radiol，2013， 116（6）： 769-73.

[5] Spin-Neto R， Costa C， Salgado DM， et al. Patient movementcharacteristics and the impact on CBCT image quality andinterpretability[J]. Dentomaxillofac Radiol， 2018， 47（1）： 20170216.

[6] Weisenberger AG， Gleason SS， Goddard J， et al. A restraint-freesmall animal SPECT imaging system with motion tracking[J].IEEE Trans Nucl Sci， 2005， 52（3）： 638-44.

[7] Herzog H， Tellmann L， Fulton R， et al. Motion artifact reduction onparametric PET images of neuroreceptor binding[J]. J Nucl Med，2005， 46（6）： 1059-65.

[8] Kim JH， Nuyts J， Kyme A， et al. A rigid motion correction methodfor helical computed tomography （CT）[J]. Phys Med Biol， 2015， 60（5）： 2047-73.

[9] Kyme AZ， Se S， Meikle SR， et al. Markerless motion estimation formotion-compensated clinical brain imaging[J]. Phys Med Biol，2018， 63（10）： 105018.

[10]Sisniega A， Stayman JW， Yorkston J， et al. Motion compensation inextremity cone-beam CT using a penalized image sharpness criterion[J]. Phys Med Biol， 2017， 62（9）： 3712-34.

[11]Maur S， Stsepankou D， Hesser J. Auto-calibration by locallyconsistent contours for dental CBCT[J]. Phys Med Biol， 2018， 63（21）： 215018.

[12]Huang H， Siewerdsen JH， Zbijewski W， et al. Reference-freelearning-based similarity metric for motion compensation in conebeamCT[J]. Phys Med Biol， 2022， 67（12）： 10.1088/1361-6560/ac749a.

[13]Hahn J， Bruder H， Rohkohl C， et al. Motion compensation in theregion of the coronary arteries based on partial angle reconstructionsfrom short-scan CT data[J]. Med Phys， 2017， 44（11）： 5795-813.

[14]Berger M， Xia Y， Aichinger W， et al. Motion compensation for conebeamCT using Fourier consistency conditions[J]. Phys Med Biol，2017， 62（17）： 7181-215.

[15]Preuhs A， Maier A， Manhart M， et al. Symmetry prior for epipolarconsistency[J]. Int J Comput Assist Radiol Surg， 2019， 14（9）：1541-51.

[16]Ouadah S， Jacobson M， Stayman JW， et al. Correction of patientmotion in cone-beam CT using 3D-2D registration[J]. Phys MedBiol， 2017， 62（23）： 8813-31.

[17]Niebler S， Schömer E， Tjaden H， et al. Projection-basedimprovement of 3D reconstructions from motion-impaired dentalcone beam CT data[J]. Med Phys， 2019， 46（10）： 4470-80.

[18]Hu ZL， Jiang CH， Zhang QY， et al. Wasserstein generativeadversarial networks for motion artifact removal in dental CTimaging[C]//Medical Imaging 2019： Physics of Medical Imaging.February 16-21， 2019. San Diego， USA. SPIE， 2019： 1094836.

[19]Su B， Wen YT， Liu YY， et al. A deep learning method for eliminatinghead motion artifacts in computed tomography[J]. Med Phys， 2022，49（1）： 411-9.

[20]Ko Y， Moon S， Baek J， et al. Rigid and non-rigid motion artifactreduction in X-ray CT using attention module[J]. Med Image Anal，2021， 67： 101883.

[21]Spin-Neto R， Matzen LH， Schropp LW， et al. An ex vivo study ofautomated motion artefact correction and the impact on cone beamCT image quality and interpretability[J]. DentomaxillofacialRadiol， 2018： 20180013.

[22]Kim JH， Sun T， Alcheikh AR， et al. Correction for human headmotion in helical X-ray CT[J]. Phys Med Biol， 2016， 61（4）：1416-38.

[23]Li XH， Da Z， Liu B. A generic geometric calibration method fortomographic imaging systems with flat-panel detectors： a detailedimplementation guide[J]. Med Phys， 2010， 37（7）： 3844-54.

[24]Li DS， Zhang Y， Cheung KC， et al. Learning degradationrepresentations for image deblurring[C]//European Conference onComputer Vision. Cham： Springer， 2022： 736-753.

[25]Park T， Liu MY， Wang TC， et al. Semantic image synthesis withspatially-adaptive normalization[C]//2019 IEEE/CVF Conferenceon Computer Vision and Pattern Recognition （CVPR）. Long Beach，CA， USA. IEEE， 2019： 2332-41.

[26]Mechrez R， Talmi I， Shama F， et al. Maintaining natural imagestatistics with the contextual loss[C]//Asian Conference onComputer Vision. Cham： Springer， 2019： 427-443.

[27]Ronneberger O， Fischer P， Brox T. U-net： convolutional networksfor biomedical image segmentation[M]//Lecture Notes inComputer Science. Cham： Springer International Publishing， 2015：234-41.

[28]Gulrajani I， Ahmed F， Arjovsky M， et al. Improved training ofWasserstein GANs[C]//Proceedings of the 31st InternationalConference on Neural Information Processing Systems. December 4‑9， 2017， Long Beach， California， USA. ACM， 2017： 5769-79.

[29]Chen LY， Lu X， Zhang J， et al. HINet： half instance normalizationnetwork for image restoration[C]//2021 IEEE/CVF Conference onComputer Vision and Pattern Recognition Workshops （CVPRW）.Nashville， TN， USA. IEEE， 2021： 182-92.

[30]Zamir SW， Arora A， Khan S， et al. Restormer： efficient transformerfor high-resolution image restoration[C]//2022 IEEE/CVFConference on Computer Vision and Pattern Recognition （CVPR）.New Orleans， LA， USA. IEEE， 2022： 5718-29.

[31]Sun T， Jacobs R， Pauwels R， et al. A motion correction approach fororal and maxillofacial cone-beam CT imaging[J]. Phys Med Biol，2021， 66（12）： 125008.

[32]Wang ZH， Chen J， Hoi SCH. Deep learning for image superresolution：a survey[J]. IEEE Trans Pattern Anal Mach Intell， 2021，43（10）： 3365-87.

（编辑：经 媛）

基金项目：国家自然科学基金（U21A6005，12226004）；广州市科技计划项目（202206010148）