基于含治愈患者生存数据的Cox-TEL方法性能的模拟研究

摘要：目的 探究针对长期生存数据的Cox比例风险模型的Taylor拓展调整（Cox-TEL）方法在含治愈患者的生存数据下的适用条件与适用范围。方法 基于Weibull分布模拟生存数据方法，模拟生成不同治愈率、删失率和治愈率差值的生存数据。然后基于Cox-TEL方法进行分析，获得Ⅰ类错误和检验效能对其表现性能进行评价。结果 针对模型的未治愈部分，Cox-TEL方法的Ⅰ类错误略高于0.05，其检验效能在样本量较大、治愈率差值较大时较为理想。针对治愈部分，Cox-TEL方法的Ⅰ类错误能够较好的控制在0.05左右，且在大多数情况下都能保持较高的检验效能。结论 Cox-TEL方法在多数情况下，比如样本量较大、删失率较低、组间治愈率差值较大时，能有效分析未治愈患者数据，得到较可靠的风险比HR值；在不同的样本量、删失率和治愈率下，该方法都能较准确地估计出治愈患者两组治愈率差值。

关键词：Cox-TEL；治愈模型；生存分析；检验效能

Cox比例风险模型［1］是生存分析方法中最经典、最常用的方法，其应用前提是需要满足等比例风险假定。然而，实践中常常会出现生存曲线存在治愈患者导致生存曲线尾部出现平台期的情况，这些情况可能会违背等比例风险假定［2， 3］。虽然已有作者提出限制性平均生存时间（RMST）［4-8］、治愈模型［9-14］等一系列方法能够对存在治愈患者的不满足等比例风险假定的生存数据进行有效分析，但在已发表的文献中仍存在较多误用Cox比例风险模型分析此类数据的情况［15-17］。针对存在一定比例治愈患者的情况，Hsu等［18］在2021年提出长期生存数据的Cox 比例风险模型的Taylor 拓展调整（Cox-TEL）方法，该方法只需基于文献中的HR值及其95%置信区间和KM曲线所估计的生存率，即可在没有原始数据的情况下，获得近似治愈模型分析所得的结果［19， 20］。然而，Cox-TEL方法的作者未明确说明其适用条件，其估计结果的可靠性及准确性尚未得到证实。因此，本研究拟通过蒙特卡罗模拟，探究该方法应用于不同情况下含治愈患者生存数据时的Ⅰ类错误和检验效能，为研究者能正确使用Cox-TEL方法以便利获得HR值以及组间治愈率差值（DP）提供参考。

1 方法

1.1 PHMC模型

治愈模型主要分为两类，混合治愈模型和非混合治愈模型［21， 22］。混合治愈模型通常假定研究人群中存在治愈和未治愈两种不同类型的患者，并分别对这两类患者进行建模［23， 24］。其中，针对未治愈患者，计算试验组相对于对照组的HR值，针对治愈患者，计算治愈率差值（DP）。DP值为试验组治愈率与对照组治愈率的差值。混合治愈模型的表达形式为：

S （t|x，z ） = π （z ） S （t|x） + 1 - π （z ）

其中π （z）是患者未治愈的概率，S （t|x，z ）是未治愈患者的生存概率，x和z是协变量的观测值。π （z ）通常被称为模型的incidence部分，S （t|x）被称为模型的latency部分，描述未治愈患者生存时间的分布。在混合治愈模型中，当latency部分使用PH（Proportion Hazard）模型时，即为PHMC模型［25］。PHMC模型的表达式如下：

S （t|x，z ） = π （z ） S0（t ）exp （ βx） + 1 - π （z ）

S0（t ）是未治愈患者在协变量x = 0 时的基线生存函数。

PHMC模型等治愈模型不仅考虑组间的短期生存率差异，同时也考虑长期生存者比例在组间的差异，即治愈率差值。因此针对存在平台期的数据利用治愈模型分析能得到更加准确的结论。

1.2 Cox-TEL方法

Cox-TEL方法主要针对KM生存曲线存在平台期的情况，即研究人群中存在一定比例的治愈患者，这类患者永远不会经历研究中感兴趣事件［18， 26］。Cox-TEL方法通过泰勒展开式找出Cox比例风险模型与PHMC模型之间的数学关系，再以此关系为基础，将Cox比例风险模型所估计的结果转换为近似PHMC模型估计的结果。Cox-TEL法不需要获取文献中所使用的原始数据，仅需要文献中Cox模型所估计出的HR值及其95%置信区间和KM曲线所估计的生存率即可获得近似PHMC模型的结果，这些值通常可直接从文献中获得。

1.3 Engauge Digitizer软件

生存分析相关文献几乎都会报告该研究对应的生存曲线图供读者参考。研究者可以通过EngaugeDigitizer软件从生存曲线中提取有价值的信息［27］。

2 模拟与实例

2.1 模拟步骤

基于已有的生存数据模拟方法［28-31］，结合具有治愈患者的生存数据的特点，生成不同情况下包含治愈患者的生存数据。考察Cox-TEL方法的Ⅰ类错误和检验效能。本研究的所有统计分析与模拟研究部分均使用R4.2.3完成。具体模拟参数见表1。

2.2 模拟结果

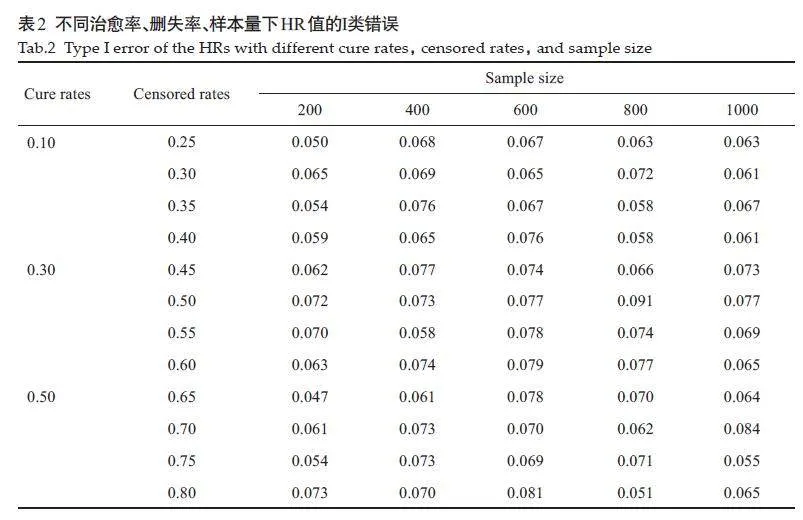
2.2.1 Cox-TEL方法HR值的Ⅰ类错误

大多数情况下，Cox-TEL方法HR值的Ⅰ类错误均略高于0.05，但Ⅰ类错误的大小并没有随着样本量、删失率、治愈率的变化而发生明显的变化（表2）。

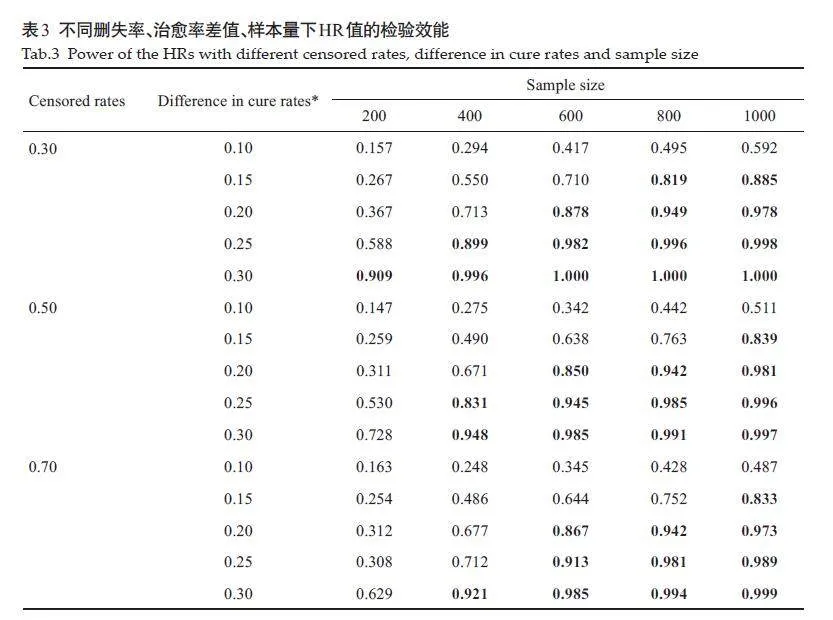
2.2.2 Cox-TEL 方法HR 值的检验效能

当样本量较大，治愈率差值较大时，检验效能大于0.8且检验效能随着样本量和治愈率差值的增大而增大（表3）。此外，在其他条件相同的情况下，删失率越低，检验效能越高。

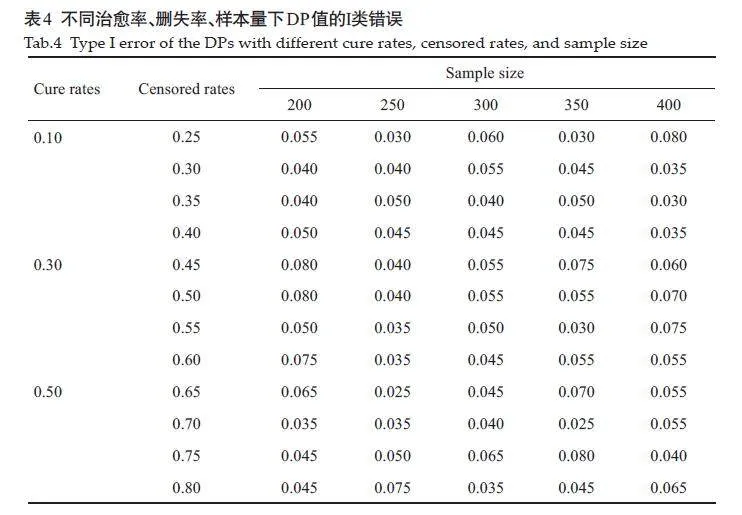
2.2.3 Cox-TEL方法DP值的Ⅰ类错误

Ⅰ类错误基本控制在0.05左右；当治愈率较低时，Ⅰ类错误较小，结果偏向于保守；随着治愈率的增大，Ⅰ类错误略有增大，但都基本控制在0.05左右（表4）。

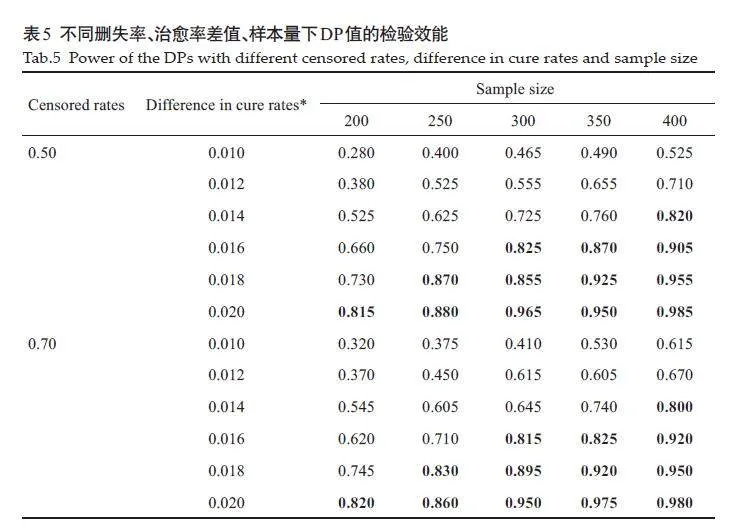
2.2.4 Cox-TEL方法DP值的检验效能

治愈率差值稍大（如≥0.020）时，检验效能基本都大于0.8且检验效能随着样本量和治愈率差值的增大而增大（表5）。

2.3 实例分析

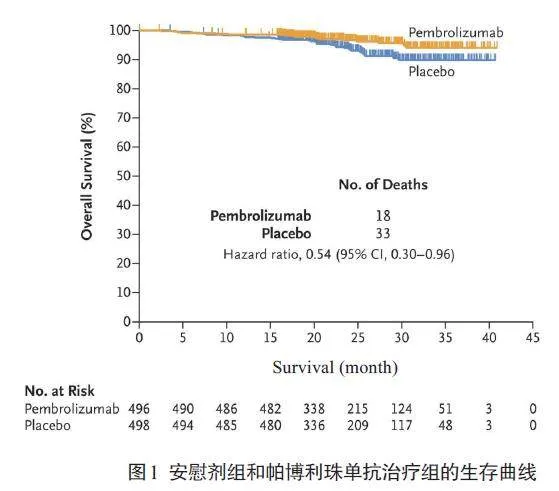
某项临床研究的目的是探讨与安慰剂相比，肾切除术后使用帕博利珠单抗治疗是否会改善患有透明细胞肾细胞癌并且有中高复发风险或高复发风险患者的结局［32］。KM生存曲线表明，在研究时间段内Cox HR 为0.54（95% CI，0.30～0.96），提示使用帕博利珠单抗治疗更有利于患者的生存（图1）。

考虑使用Cox-TEL方法，重新对上述研究进行分析。利用Engauge digitizer软件提取生存曲线图中相关点对应的生存率和时间，并使用提取的数据进行分析。

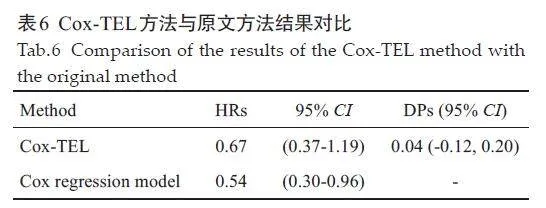
由表6 可见两种方法结果存在差异，Cox-TEL HR值的95% CI包含1，在未治愈患者部分中，并不能认为安慰剂组和帕博利珠单抗治疗组之间的差异具有统计学意义。Cox-TEL DP值为0.04（95% CI，-0.12～0.20），尚不能认为两组中治愈患者占比差异有统计学意义。

3 讨论

本文通过模拟生成生存数据，探讨在不同治愈率、删失率和治愈率差值的情况下，Cox-TEL方法的Ⅰ类错误和检验效能。结果表明，多数情况下Cox-TEL方法HR 值的Ⅰ类错误略大于0.05，检验效能可以保持较高水平。但在样本量较少（如lt;200）、治愈率差值较小（如lt;0.2）的情况下检验效能偏低。Cox-TEL方法DP值的Ⅰ类错误基本能够控制在0.05左右，且检验效能在大多数情况下也能保持在gt;0.8的较高水平。该方法能有效分析未治愈患者数据，得到较为可靠的HR值，并且能较准确地估计出治愈患者两组治愈率差值。

在生存分析中，经典方法为Cox比例风险模型，但实际应用中常会出现生存曲线交叉或存在平台期的情况，此时使用Cox 比例风险模型得出的结论存疑［15-17］。这些已发表的研究文献中一般无法获得原始数据，但通常会给出相应的生存曲线。此时，可先使用Cox-TEL方法对HR值进行估计，再结合已有的Cox比例风险模型的HR值，确定真实HR值的大致范围，以供后继研究者参考。实际运用中，若不满足比例风险假定，但能获得原始数据，则可在使用Cox-TEL 方法前考虑用PHMC模型［14］或其他更加适合的模型进行分析［5］。在删失率较高（如gt;0.3）、组间治愈率差值较大（如gt;0.2）的情况下，Cox-TEL方法可靠性较差。

Cox-TEL方法不需原始数据，仅从文献给出的生存曲线和部分指标就可获得具有一定准确度的HR值和DP值结果，使后续研究者能正确看待前人不适当使用Cox比例风险模型的研究结果并能相对简便地获得更接近真实的结果。本研究存在以下不足，Cox-TEL方法是将Cox 比例风险模型所估计的结果转换为近似PHMC模型估计的结果，但在本研究中，只探讨了Cox-TEL方法的性能，并未研究其与PHMC模型分析结果的一致性。此外，该研究模拟时仅考虑了一个二分类处理因素的情况，尚未延伸到多个处理因素的情况。

参考文献：

[1] Cox DR. Regression models and life-tables[J]. J R Stat Soc Ser BStat Methodol， 1972， 34（2）： 187-202.

[2] Jayk Bernal A， Gomes da Silva MM， Musungaie DB， et al.Molnupiravir for oral treatment of covid-19 in nonhospitalizedpatients[J]. N Engl J Med， 2022， 386（6）： 509-20.

[3] Tawbi HA， Schadendorf D， Lipson EJ， et al. Relatlimab andnivolumab versus nivolumab in untreated advanced melanoma[J].N Engl J Med， 2022， 386（1）： 24-34.

[4] 康 佩， 许 军， 黄福强， 等. Adaptive Elastic Net结合加速失效时间模型在亚组识别中的应用[J]. 南方医科大学学报， 2019， 39（10）：1200-6.

[5] El Sharouni MA， Ahmed T， Varey AHR， et al. Development andvalidation of nomograms to predict local， regional， and distantrecurrence in patients with thin （T1） melanomas[J]. J Clin Oncol，2021， 39（11）： 1243-52.

[6] An SL， Zhang P， Fang HB. Subgroup identification in survivaloutcome data based on concordance probability measurement[J].Mathematics， 2023， 11（13）： 2855.

[7] 黄福强， 康 佩， 刘颖欣， 等. 含治愈个体生存资料的亚组识别研究[J]. 中国卫生统计， 2020， 37（5）： 672-7.

[8] 韦红霞， 康 佩， 刘颖欣， 等. 基于Adaptive Elastic Net与加速失效时间模型的亚组识别方法的应用拓展[J]. 南方医科大学学报， 2021，41（3）： 391-8.

[9] Peng Y， Dear KB. A nonparametric mixture model for cure rateestimation[J]. Biometrics， 2000， 56（1）： 237-43.

[10]Sy JP， Taylor JM. Estimation in a Cox proportional hazards curemodel[J]. Biometrics， 2000， 56（1）： 227-36.

[11] Lo SN， Scolyer RA， Thompson JF. Long-term survival of patientswith thin （T1） cutaneous melanomas： a Breslow thickness cut pointof 0.8mm separates higher-risk and lower-risk tumors[J]. Ann SurgOncol， 2018， 25（4）： 894-902.

[12]Lu WB. Maximum likelihood estimation in the proportional hazardscure model[J]. Ann Inst Stat Math， 2008， 60（3）： 545-74.

[13]Royston P， Parmar MK. Restricted mean survival time： analternative to the hazard ratio for the design and analysis ofrandomized trials with a time-to-event outcome[J]. BMC Med ResMethodol， 2013， 13（1）： 152.

[14]Ghobadi KN， Roshanaei G， Poorolajal J， et al. The estimation oflong and shrt term survival time and associated factors of HIVpatients using mixture cure rate models[J]. BMC Med ResMethodol， 2023， 23（1）： 123.

[15]Castellino SM， Pei QL， Parsons SK， et al. Brentuximab vedotin withchemotherapy in pediatric high-risk Hodgkin's lymphoma[J]. NEngl J Med， 2022， 387（18）： 1649-60.

[16]Mirza MR， Chase DM， Slomovitz BM， et al. Dostarlimab forprimary advanced or recurrent endometrial cancer[J]. N Engl JMed， 2023， 388（23）： 2145-58.

[17]Gounder M， Ratan R， Alcindor T， et al. Nirogacestat， a γ-secretaseinhibitor for desmoid tumors[J]. N Engl J Med， 2023， 388（10）：898-912.

[18]Hsu CY， Lin EPY， Shyr Y. Development and evaluation of a methodto correct misinterpretation of clinical trial results with long-termsurvival[J]. JAMA Oncol， 2021， 7（7）： 1041-4.

[19]Lin EP， Hsu CY， Berry L， et al. Analysis of cancer survivalassociated with immune checkpoint inhibitors after statisticaladjustment： a systematic review and meta-analyses[J]. JAMA NetwOpen， 2022， 5（8）： e2227211.

[20]Lin EPY， Hsu CY， Chiou JF， et al. Cox proportional hazard ratiosoverestimate survival benefit of immune checkpoint inhibitors： cox-TEL adjustment and meta-analyses of programmed death-ligand 1expression and immune checkpoint inhibitor survival benefit[J]. JThorac Oncol， 2022， 17（12）： 1365-74.

[21]Othus M， Barlogie B， Leblanc ML， et al. Cure models as a usefulstatistical tool for analyzing survival[J]. Clin Cancer Res， 2012， 18（14）： 3731-6.

[22]Webb A， Ma J， Lô SN. Penalized likelihood estimation of a mixturecure Cox model with partly interval censoring-An application to thinmelanoma[J]. Stat Med， 2022， 41（17）： 3260-80.

[23]Zhou XX， Song XY. Mediation analysis for mixture Coxproportional hazards cure models[J]. Stat Methods Med Res， 2021，30（6）： 1554-72.

[24]Wang SF， Zhang JJ， Lu WB. Sample size calculation for theproportional hazards cure model[J]. Stat Med， 2012， 31（29）：3959-71.

[25]Cai C， Zou YB， Peng YW， et al. Smcure： an R-package forestimating semiparametric mixture cure models[J]. ComputMethods Programs Biomed， 2012， 108（3）： 1255-60.

[26]Kuk AYC， Chen CH. A mixture model combining logistic regressionwith proportional hazards regression[J]. Biometrika， 1992， 79（3）：531-41.

[27]Xue YY， Li GP， Xie T， et al. Concurrent chemoradiotherapy versusradiotherapy alone for stage II nasopharyngeal carcinoma in the eraof intensity-modulated radiotherapy[J]. Eur Arch Otorhinolaryngol，2023， 280（7）： 3097-106.

[28]肖媛媛， 陈 莹， 何利平， 等. 不同删失比例下AFT模型与Cox模型表现比较的模拟研究[J]. 中国卫生统计， 2017， 34（4）： 676-80.

[29]钱 俊， 刘国庆， 周业明. 不同删失比例下生存数据模拟生成的方法[J]. 数理医药学杂志， 2013， 26（6）： 644-6.

[30]肖媛媛， 许传志， 赵耐青. 含特定比例均匀随机删失生存数据的SAS模拟实现[J]. 中国卫生统计， 2016， 33（6）： 1058-9， 1062.

[31]蔡丽馨， 仲子航， 杨 旻， 等. 指定删失比例的生存数据模拟及R实现[J]. 中国卫生统计， 2022， 39（1）： 143-8.

[32]Choueiri TK， Tomczak P， Park SH， et al. Adjuvant pembrolizumabafter nephrectomy in renal-cell carcinoma[J]. N Engl J Med， 2021，385（8）： 683-94.

（编辑：吴锦雅）

基金项目：广东省自然科学基金（2022A1515012152）；南方医科大学2022 年度大学生创新创业训练计划项目（S202212121135）