基于ANSYS/APDL的织物导热性能影响因素

摘 要：为研究织物导热性能的影响因素，提出了一种基于ANSYS的织物热传递有限元仿真二次开发系统。利用ANSYS/APDL软件对织物进行参数化建模，模拟分析在不同织物组织、织物紧度、经纬纱线材料条件下，织物中的热量传递过程及温度分布特征，并计算各织物的导热系数和蓄热系数。使用C-THERM TCi导热仪对织物样本的导热系数和蓄热系数进行测试，与模拟计算结果对比，发现模拟同实验测试结果的绝对误差值在4%以内，验证了该模型的有效性，并进一步探究了织物导热性能的影响因素。结果表明：在相同条件下，平纹织物的蓄热系数和导热系数最高，斜纹次之，缎纹最低；随着织物紧度的增加，织物的导热系数和蓄热系数也升高；随着纱线导热系数的上升，织物的导热系数和蓄热系数升高。研究结果对织物导热性能的参数化模拟仿真及良好导热性能的织物开发具有重要意义。

关键词：有限元仿真；导热性能；参数化建模；导热系数；蓄热系数

中图分类号：TS15

文献标志码：A

文章编号：1009-265X（2024）10-0102-12

随着人们对织物热舒适性的要求提高，具有良好导热性能的面料成为研究热点。在炎热的夏季，导热性能良好的面料能快速将身体产生的热量传输到外界环境，给人体提供舒适、凉爽的穿着体验。织物导热性能受多种因素影响，包括织物组织结构、织物紧度、纱线导热系数、纤维含量以及织物后处理方式等［1］。因此，研究这些影响因素，对后续开发良好导热性能的织物具有重要意义。

研发导热性能良好的织物，传统的方式是织造大量织物样本并通过一系列物理测试方法，分析织物导热性能是否符合要求，这一传统方法存在工序复杂、时间长、浪费原材料的问题。相较于传统实验方法，有限元分析系统能快速获取导热系数、热阻、蓄热系数、克罗值等织物导热性能指标，有助于更有效地进行织物设计［2］。近年来，研究人员倾向于运用ANSYS、ABAQUS等有限元软件来模拟和预测织物的导热性能，为高质量、低成本的织物产品评估和优化提供有效途径［3］。

李瑛慧等［3］使用AutoCAD软件构建了织物的三维模型，通过ANSYS软件进行有限元分析，以纤维导热性参数预测织物的导热性能，并提出了一种有效预测克罗值和织物表面温度变化的方法。张洁等［4］引入牛顿插值法对纱线中心线方程进行拟合并建立织物三维模型，在ABAQUS软件中模拟平纹织物导热过程，验证了模型的有效性，并研究了空气及织物厚度对织物克罗值的影响。Siddiqui等［5］利用TexGen构建了平纹织物的单胞结构模型，预测并验证了织物的有效导热系数和热阻，同时探讨了纤维导热系数和纤维体积分数对有效导热系数的影响。Wu等［6］考虑纤维各向异性热传导，建立了不同结构参数的棉织物导热模型，采用有限元和实验相结合的方法，研究了织物的组织结构、纱线细度对织物热性能的影响。

尽管ANSYS等有限元软件在纺织领域已经广泛应用，但由于CAE模块仿真分析环境的限制，直接分析织物的导热性能及数据处理仍然具有挑战性［7-8］。因此本文通过ANSYS/APDL二次开发技术，开发一种织物热传递有限元仿真二次开发系统。首先试织不同组织结构、纱线材料、经纬纱线组合的织物样本，再利用显微成像测量织物结构参数，进行参数化建模，并利用有限元软件建立“环境-织物-皮肤”的简化三维有限元模型［9］，模拟织物在穿着过程中热量的传递过程及温度分布特征，计算织物的导热系数和蓄热系数。其次，使用C-THERM TCi导热仪对织物样本的导热系数和蓄热系数进行测试，通过实验测试和模拟结果的对比以验证该模型的有效性，同时对系统的精度与有效性进行分析。最后通过有限元模拟，研究织物组织结构、织物紧度、纱线导热系数对织物导热性能的影响。通过对织物导热性能的参数化模拟仿真为后续开发良好导热性能的织物提供条件。

1 几何模型

1.1 织物试样织造

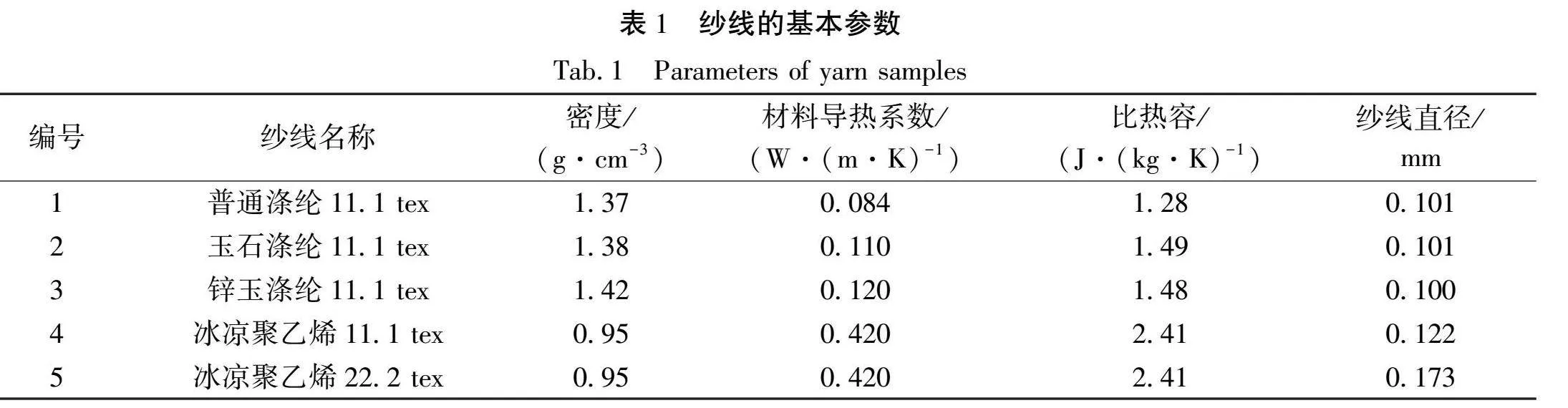
在有限元数值模拟问题中，确保模型的准确建立是分析的基础。采用绍兴喜能纺织科技有限公司生产的不同规格的纱线，通过控制变量，设计不同织物组织、不同经纬纱密度、不同经纬纱组合的织物，并进行实验织造，以确保模型数据的可靠性。优选不同导热性能的普通涤纶纱线、玉石涤纶纱线、锌玉涤纶纱线、冰凉聚乙烯纱线作为织造材料。纱线的基本参数如表1所示，织物试样规格及结构参数如表2所示，织物织造样本如图1所示。

1.2 参数化建模

在进行有限元分析之前，需要创建织物的三维几何模型。目前已有TexGen、TexEng、WiseTex等软件可生成织物的三维几何模型，但这些软件受限于各自的环境，需要将几何模型导入其他有限元分析软件，且由于CAE模块的限制，无法直接进行织物导热性能的分析［7］。通过利用ANSYS/APDL二次开发，可以在ANSYS环境中直接生成织物的三维几何模型，并可直接用于有限元分析，为后续研究提供便利。因此，在有限元软件中对织物进行参数化建模具有重要意义。

通过显微图像法获取织物几何结构参数，可以实现对织物物理模型的准确参数化建立。利用由日本电子（JEOL）生产的5610LV扫描电镜，在50倍放大条件下观察各织物织造样本的结构形态。通过对织物试样显微成像的尺寸测量，获得细观模型的几何参数。织物纬向横截面如图2所示。

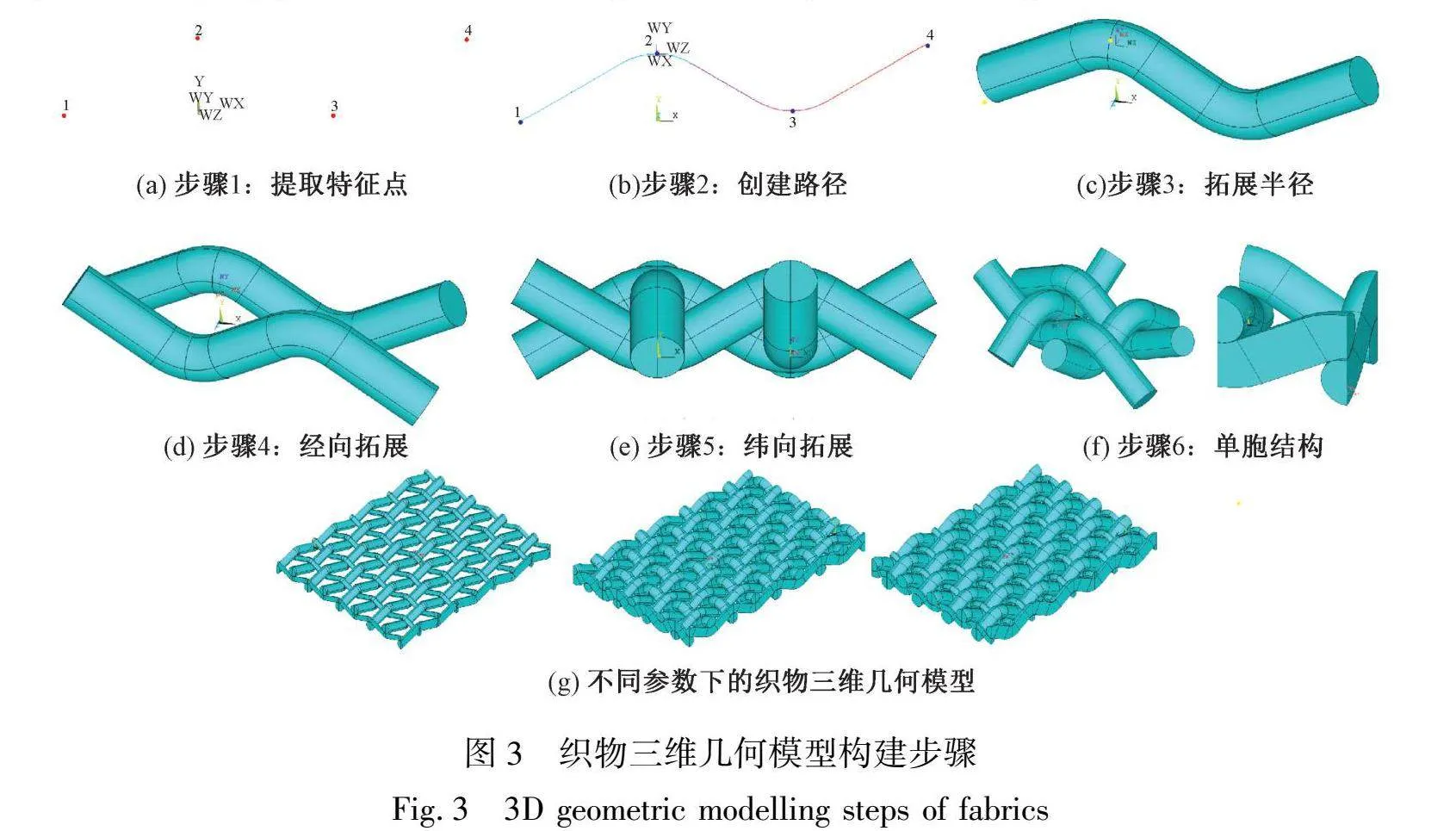
基于纱线屈曲状态，提取织物的多个特征点，利用牛顿插值公式［10］，对平纹组织、2/1斜纹组织及5/3经面缎纹组织，建立经纱和纬纱中心线的曲线方程，进而确定经纬纱线中心线轨迹，并在APDL软件中依据纱线横截面及纱线中心线路径建立织物几何模型。织物三维几何模型构建步骤如图3所示。为了方便织物建模和有限元分析，基于纱线等效原理，在构建模型过程中，假设各纱线基本性能、纱线均匀性、纱线几何参数等条件保持恒定不变［11］。

2 有限元分析及实验验证

2.1 网格划分

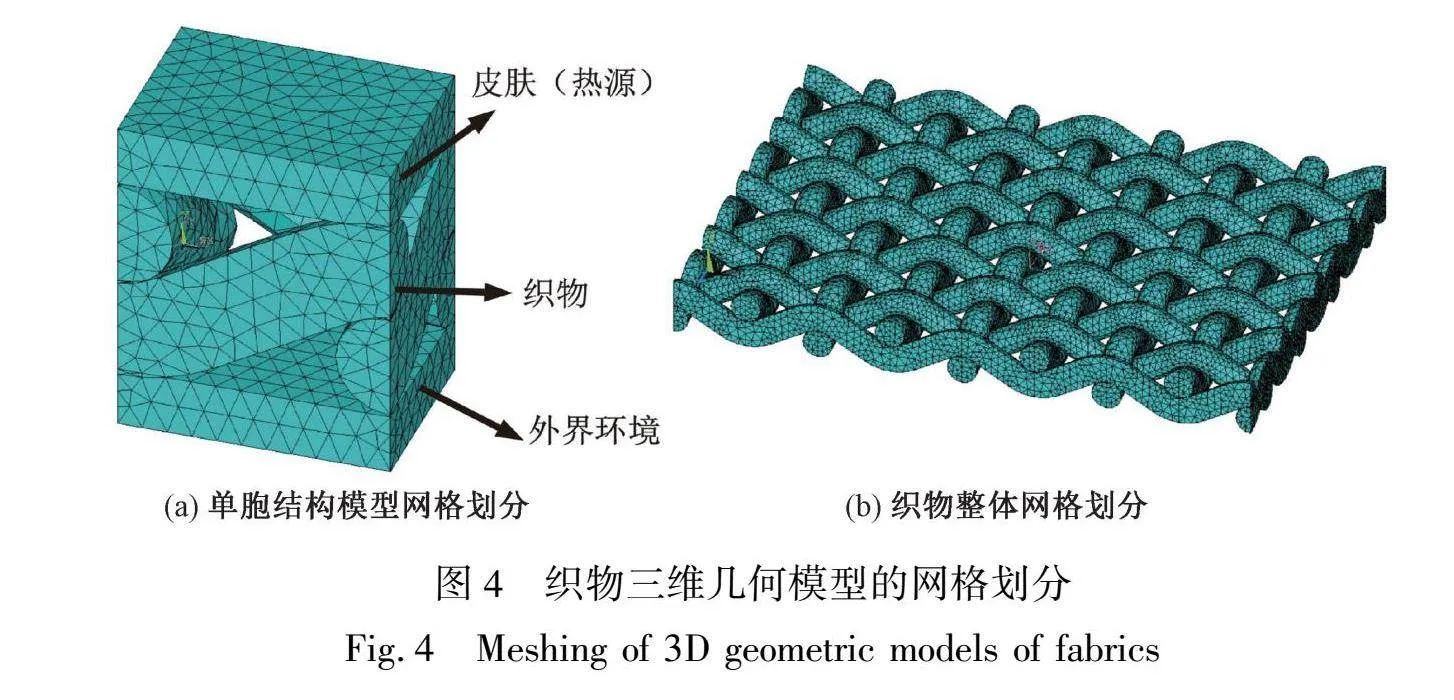
采用四节点线性四面体元素（DC3D4）对织物单胞结构模型和整体织物模型进行网格划分［12］，以确保热量在织物中传递的模拟仿真获得高质量的结果。经验证，进一步网格细化并不会对结果产生较大影响，即得到了适合的网格密度。织物三维几何模型的网格划分如图4所示。

2.2 热传递分析

对织物热传递的有限元分析做出以下假设：只考虑织物内部和表面的静止空气；热量只通过热传导传递；纱线是一种多孔材料，由纤维和空气组成；织物中的空气被认为是流体矩阵［12］，空气的导热系数为常数0.026 W/（m·K）。

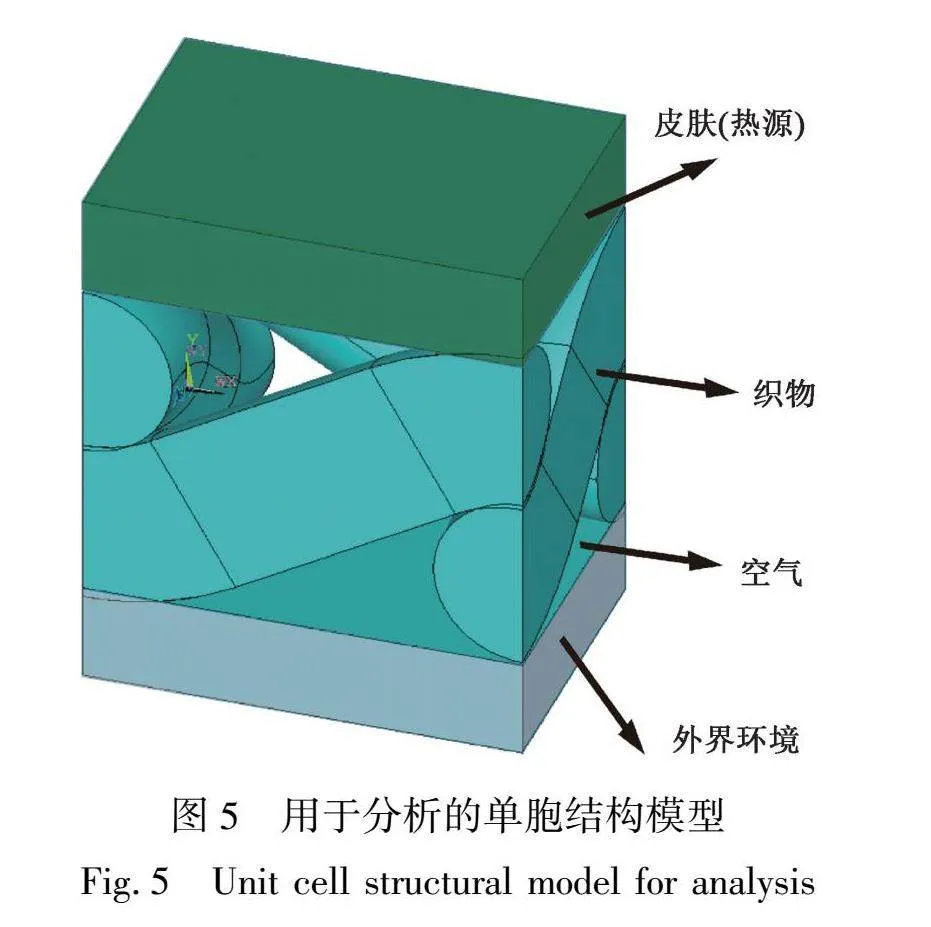
构建“环境-织物-皮肤”的三维结构模型，皮肤作为恒定热源，外界环境设定为恒定室温。用于有限元分析的单胞结构模型如图5所示。对于织物厚度上的一维稳态导热分析，必须在织物的两侧定义两个指定温度［13］。假设织物的所有其他表面都完全隔热，织物正面和背面的指定温度可以表示为T0和T1。

通过在程序中定义纱线的材料参数、织物属性和模拟边界条件，模拟织物在人体穿着状态下的热量传递过程，并获取热量分布情况。利用“环境-织物-皮肤”的热传递仿真系统，对织物热流量和节点

T0=295.15 K

T1=310.15 K

温度等数据进一步分析。织物正反面及整体温度分布如图6所示。

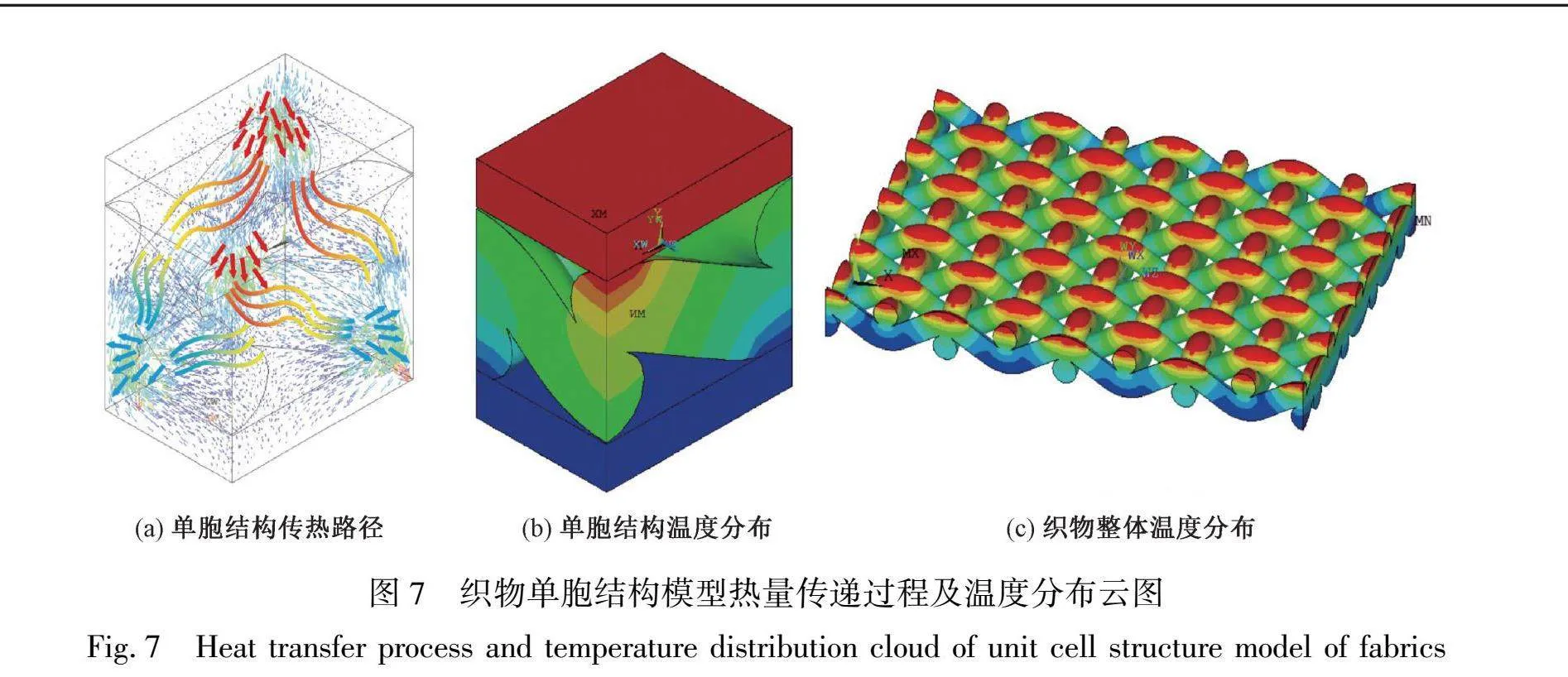
采用织物单胞结构模型计算织物的等效比热和等效质量密度，同时基于温度场模拟计算织物的导热系数和蓄热系数。织物单胞结构模型热量传递过程及温度分布云图如图7所示。

2.3 导热系数及蓄热系数计算

通过对织物进行热传递模拟，用织物正面和背面的热通量来量化织物吸收的热量，织物单胞结构模型的总热通量值ΔＱ可以用式（1）计算［14］：

ΔＱ=Ｑ/S（1）

式中：ΔＱ为总热通量值，J；Ｑ为截面总热通量，J·m2；S为总表面积，m2。

当热量达到平衡时，计算出织物升高的温度，用式（2）进一步RezmQFVCWBdViJrKhsipXQ==求出织物的平均比热容：

cρ=ΔＱ/（m·ΔT）（2）

式中：cρ为比热容，J/（kg·K）；ΔＱ为总热通量值，J；m为织物质量，kg；ΔT为升高的温度，K。

在求得织物吸收总热量的基础上，根据式（3）—（4）（傅里叶传热定律）确定织物导热系数：

q=λALΔT（3）

λ=qLAΔT（4）

式中：λ为导热系数，W/（m·K）；q为织物的热流， W；A为截面积，m2；L为织物厚度，m；ΔT为升高的温度，K。

在求得织物导热系数和平均比热容的基础上，根据公式（5）计算出织物的蓄热系数e：

e=λ·cρ·ρ（5）

式中：e为蓄热系数，（W·S1/2）/（m2·K）；λ为导热系数，W/（m·K）；cρ为比热容，J/（kg·K）；ρ为织物密度，kg/m3。

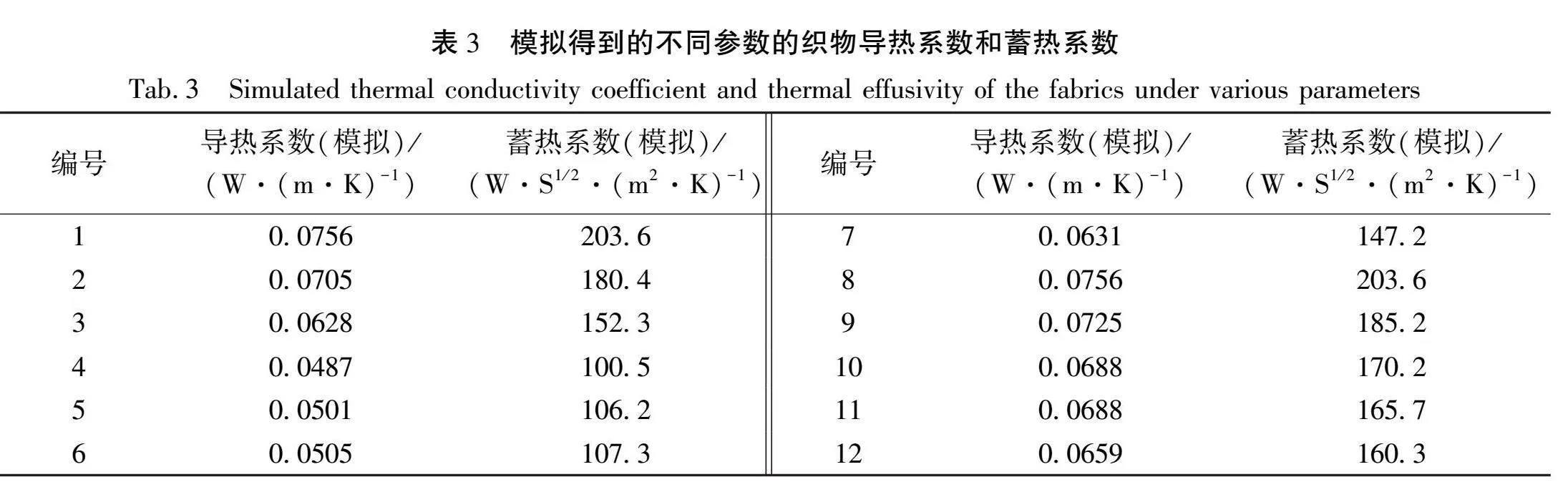
通过有限元模拟得到的不同参数的织物导热系数和蓄热系数如表3所示。

2.4 实验验证

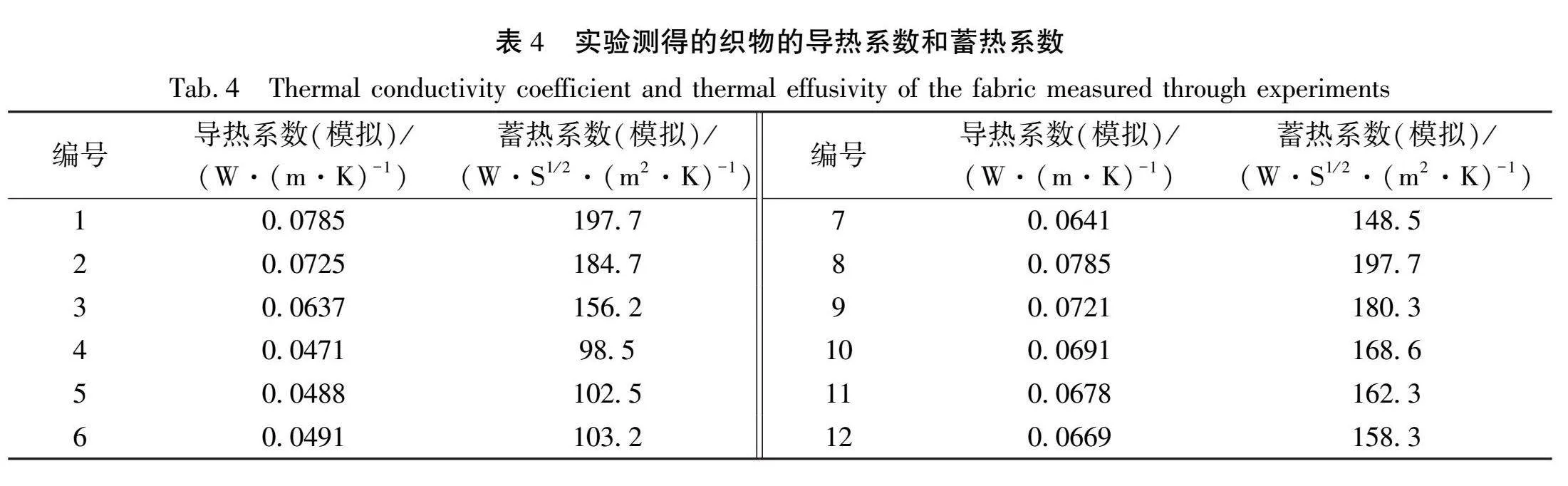
使用C-THERM TCi导热仪对织物进行导热性能测试，可一次性测量获得织物的导热系数和蓄热系数［15］。C-THERM TCi导热仪实验设备及其示意图如图8所示。在标准条件下（室温22 ℃、相对湿度65%），将织物样品放置于仪器中24 h，并在相同温湿度条件下进行测试。在测试过程中，确保样品牢固安装在测试仪器的样品夹具上，以确保仪器探头与样品表面紧密接触，避免不必要的热损失［16］。实验测得的织物的导热系数及蓄热系数如表4所示。

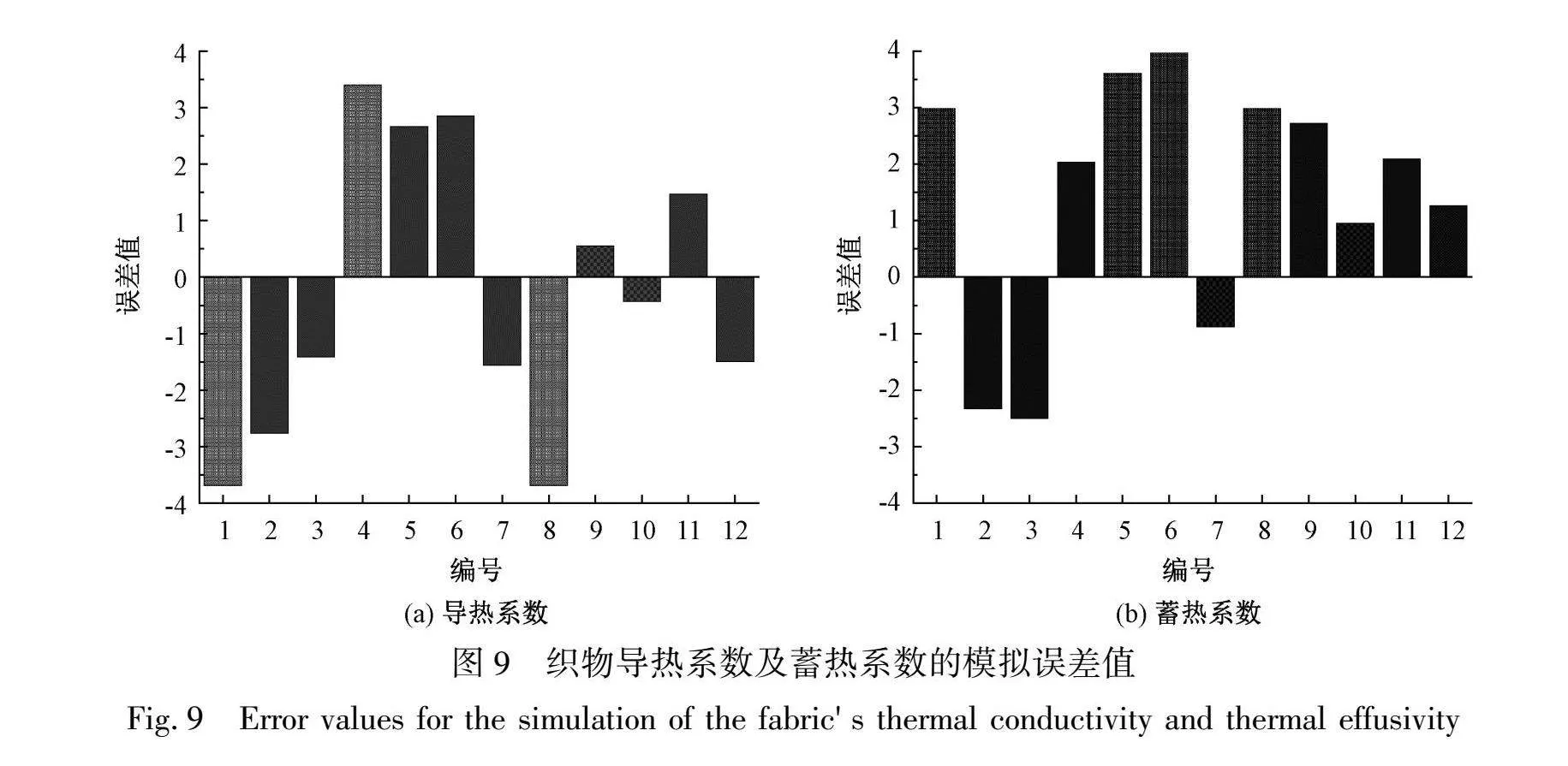
将有限元模型预测的织物导热系数和蓄热系数与实验测试结果进行比较，根据公式（6）计算误差值，验证有限元分析系统预测织物导热性能的可行性。如果在误差范围内，说明该系统的准确性和可靠性。织物导热系数及蓄热系数的模拟误差值如图9所示。

E/%=（A-B）/B×100（6）

式中：E为误差值，%；A为模拟结果；B为实验结果。

将有限元模型预测的导热系数和蓄热系数与实验结果进行对比，导热系数及蓄热系数的绝对误差值在4%以内。这表明开发的有限元分析系统对织物导热系数和蓄热系数的预测具有较高的准确性，模拟结果较为良好。模拟结果与实验结果有所差异，原因可能是纱线存在毛羽或松散现象，导致实际情况纤维在纱线中的比例与实际情况存在误差，进而造成温度上升的差异。其次模型侧面与外界的热交换及热辐射带来的热量损失也对结果有一定的影响。但是，该有限元分析系统精度较高，可被应用于预测织物的导热性能，且适用于后续对织物导热性能影响因素的研究。

3 织物导热性能影响因素的分析

本文基于织物导热机理和有限元分析方法，探究织物相关参数与导热性能间的关系。通过优化3个关键变量，即织物组织结构、织物紧度和纱线导热系数，研究它们对织物导热性能的影响，以期为设计良好导热性能织物提供有效指导。

3.1 织物组织结构对织物导热性能的影响

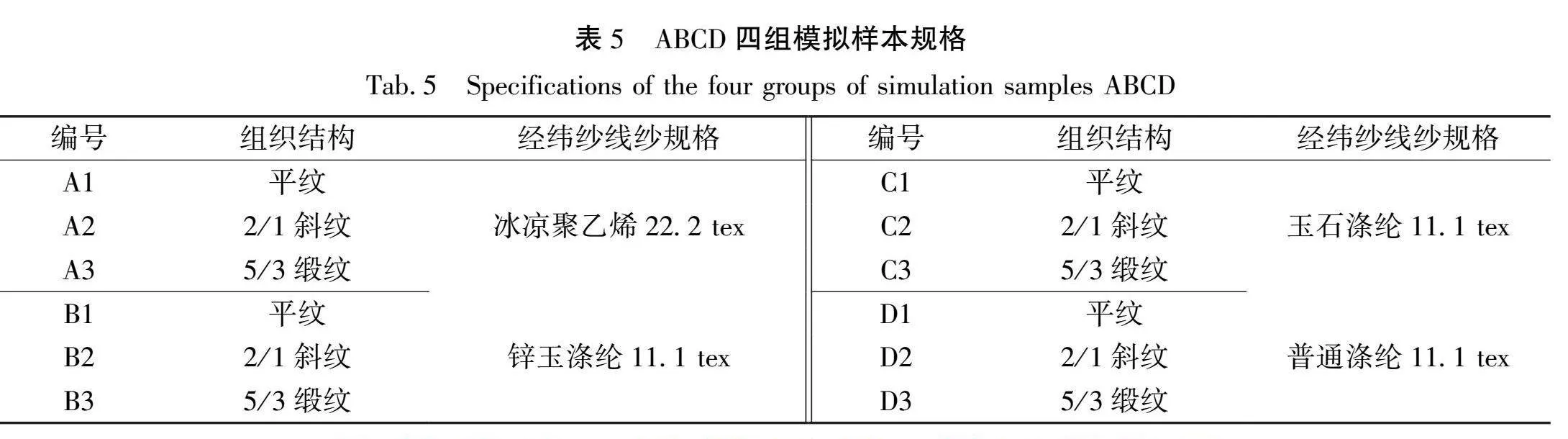
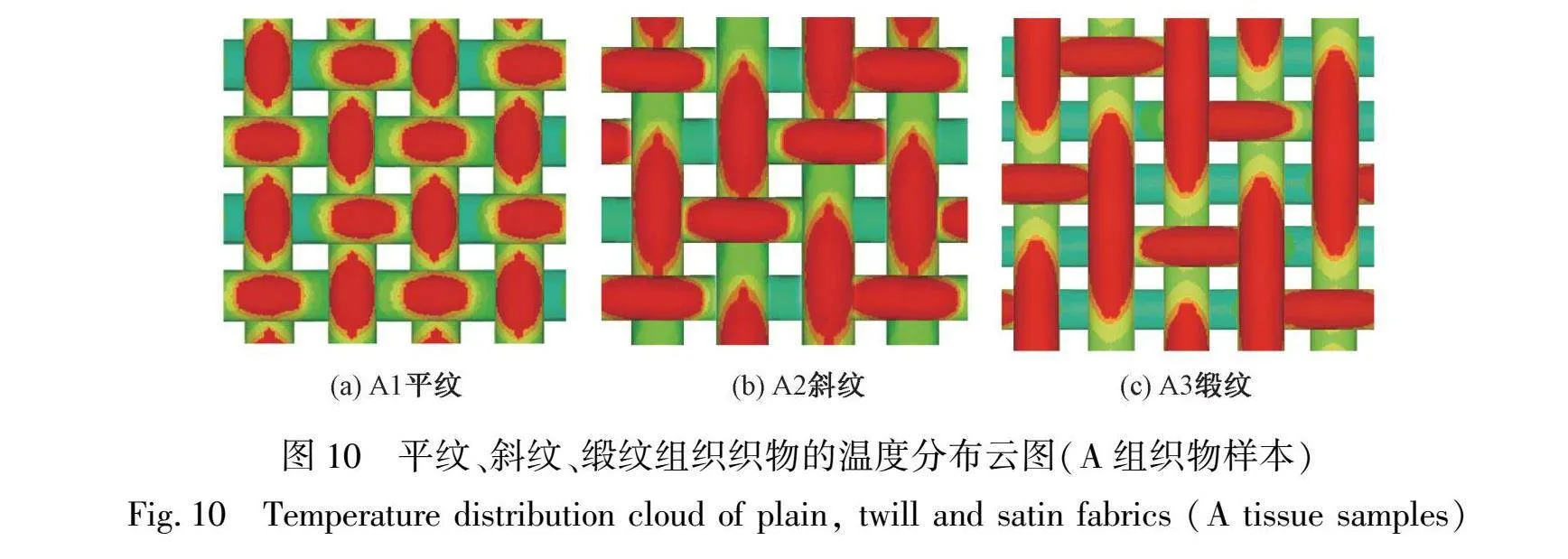
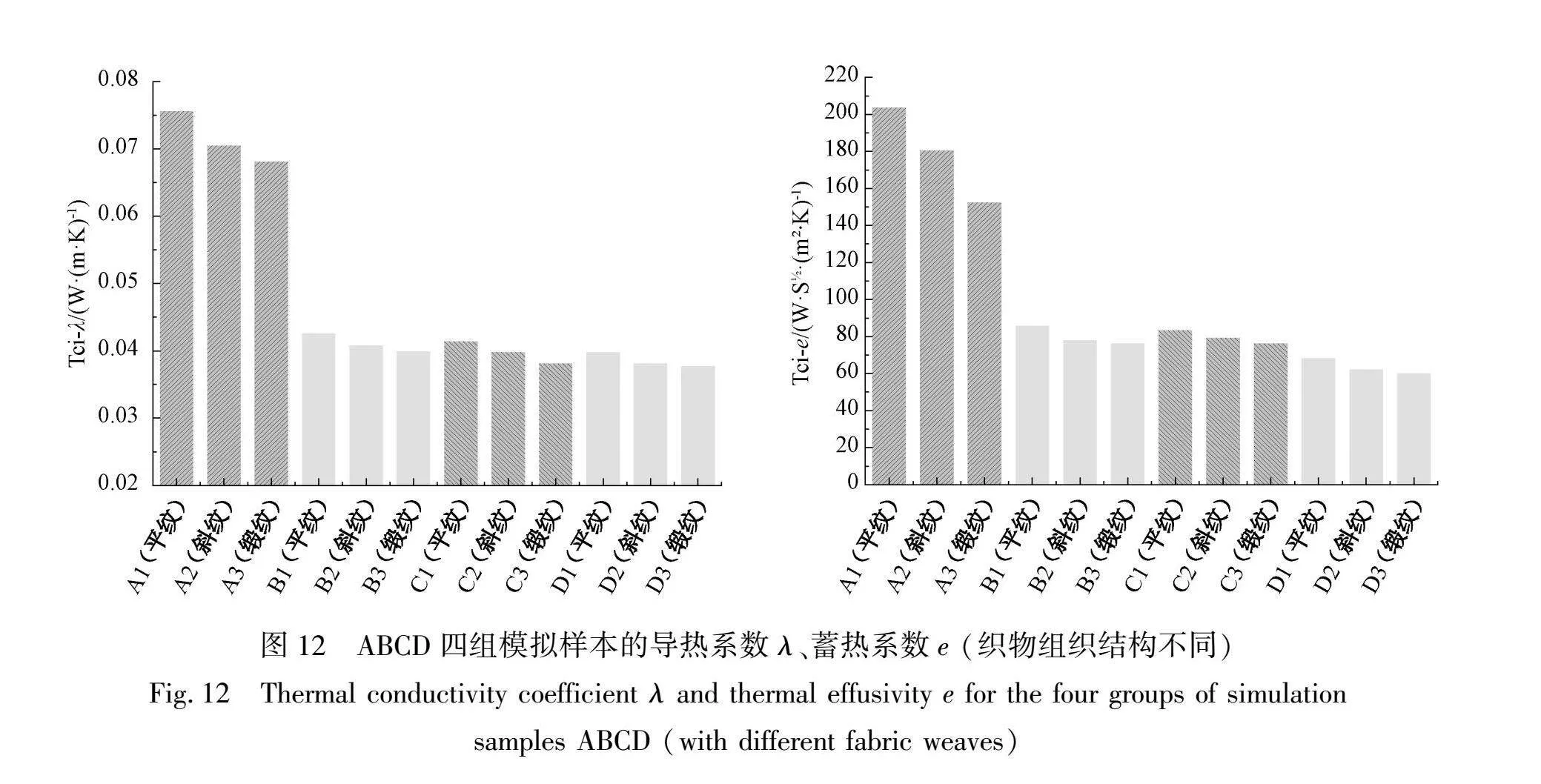
借助织物有限元导热模型，研究织物组织结构对织物导热性能的影响。控制变量，改变织物组织结构，设计ABCD四组模拟样本进行有限元模拟。通过将织物相关参数输入有限元仿真系统，模拟织物的热传递过程，求出蓄热系数和导热系数。ABCD四组模拟样本的规格（织物经密均为320根/（10cm），纬密均为280根/（10cm））如表5所示，平纹、斜纹、缎纹组织织物的温度分布云图（以A组织物样本为例）如图10所示，平纹、斜纹、缎纹组织织物表面的温度变化曲线（A组织物样本）如图11所示，ABCD四组模拟样本的蓄热系数、导热系数如图12所示。

通过设计不同织物组织结构的模拟样本，研究了织物组织结构对织物导热性能的影响。平纹织物是由上下交织的经纱和纬纱组成，斜纹织物则至少由3根经纱和3根纬纱组成，而缎纹织物则至少由5根经纱和5根纬纱组成其交织结构。织物的导热性能受到纱线和空气导热性能的共同影响，而纱线的导热性能明显优于空气。在相同的织物紧度下，缎纹织物的纱线交织点最少，整体结构更为松散，织物厚度更大，同时含有更多的静止空气。对比平纹织物、斜纹织物和缎纹织物表面的温度分布云图和温度变化曲线，3种织物表面温度到达平衡的时间依次增大，且平衡状态的温度依次降低。不同组织结构的织物，平纹织物表现出最高的蓄热系数和导热系数，斜纹织物次之，而缎纹织物则最低。

3.2 织物紧度对织物导热性能的影响

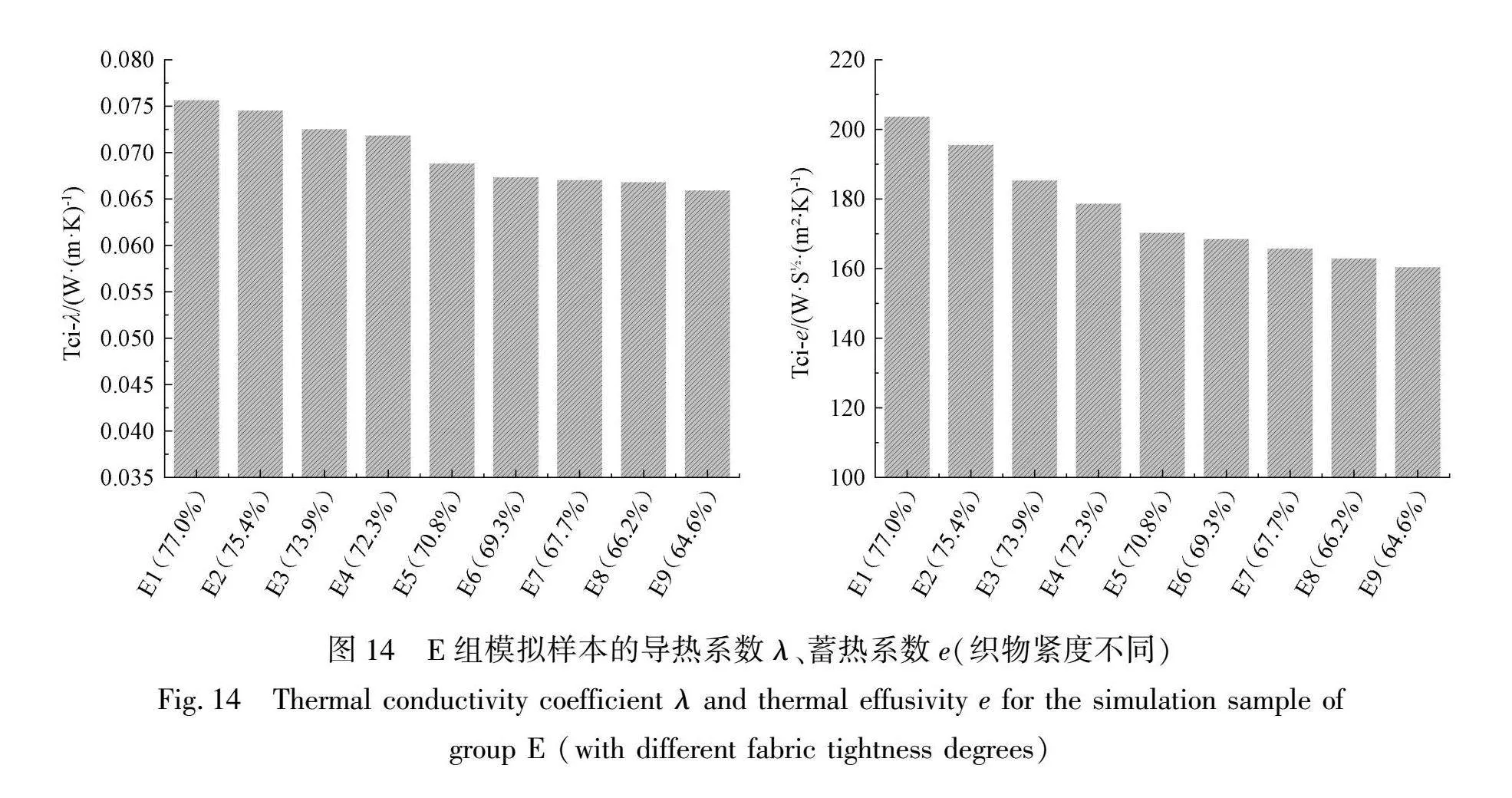
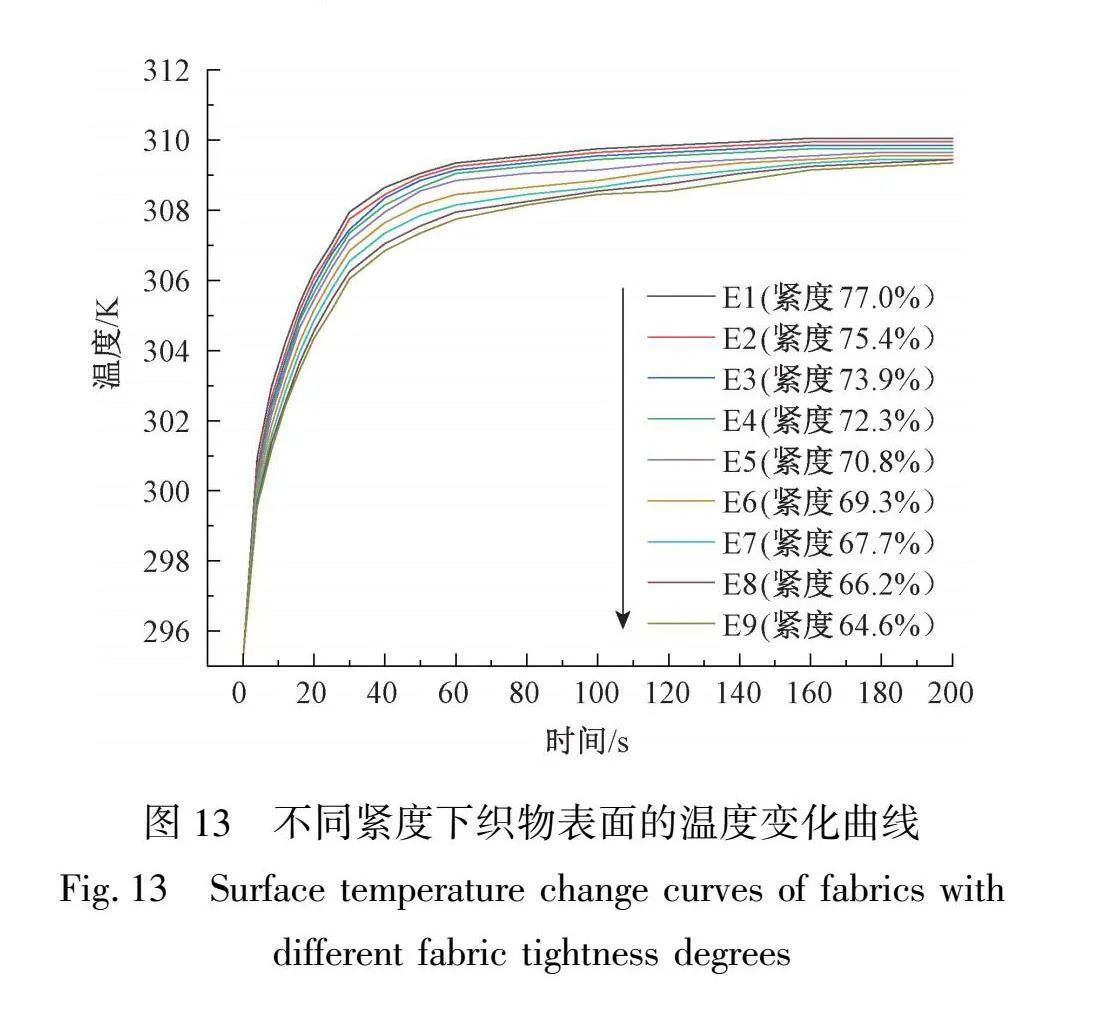
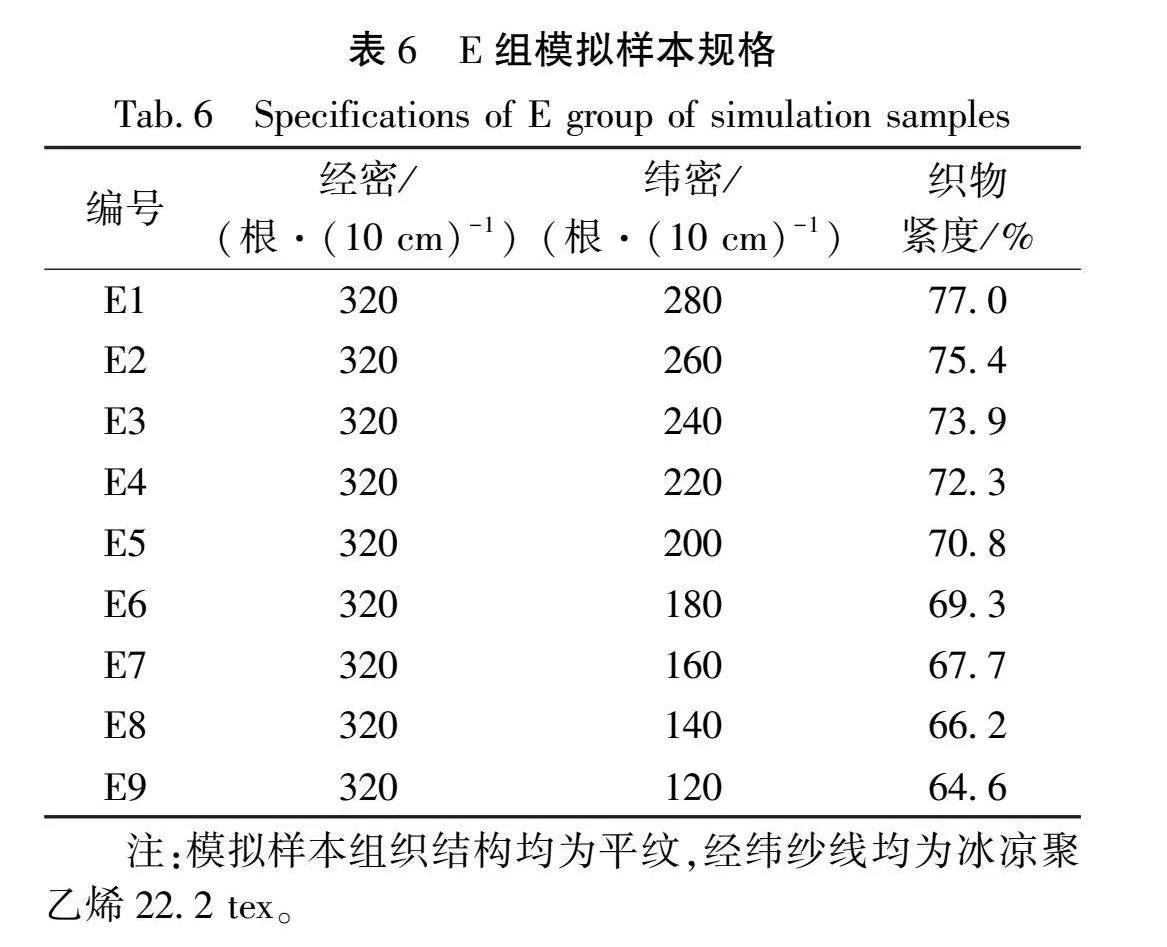
借助织物有限元导热模型，研究织物紧度对织物导热性能的影响。控制变量，改变织物紧度，设计E组模拟样本进行有限元模拟，并进行相同上述模拟操作。E组模拟样本的规格如表6所示，以平纹组织为例，经纬纱线均为冰凉聚乙烯22.2 tex，不同紧度下织物的温度变化曲线如图13所示，E组模拟样本的蓄热系数、导热系数如图14所示。

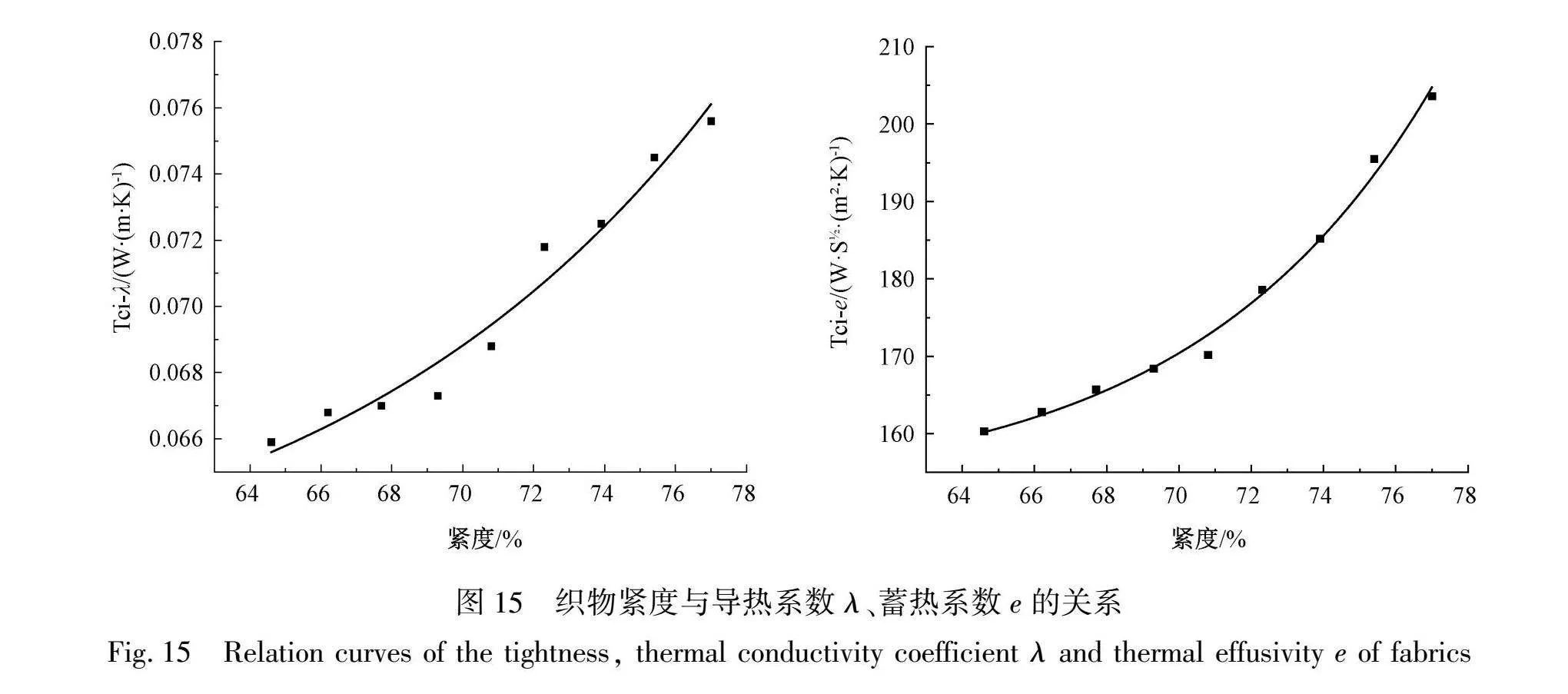
通过设计不同织物紧度的模拟样本，研究了织物紧度对织物导热性能的影响。织物紧度与织物的导热系数及蓄热系数之间存在密切关系，如图15所示。

随着织物紧度的提高，纱线在单位体积内的含量增加，空气的含量相应减少，而纱线的导热性能明显优于空气，从而整体导热性能得到提升。对比不同紧度下织物表面的温度分布云图和温度变化曲线，随着织物紧度增加，单位时间内织物的温度升高更显著。同时，织物的蓄热系数和导热系数也呈现增大的趋势，即织物的热传导能力随着织物紧度的增加而增强。

3.3 纱线导热系数对织物导热性能的影响

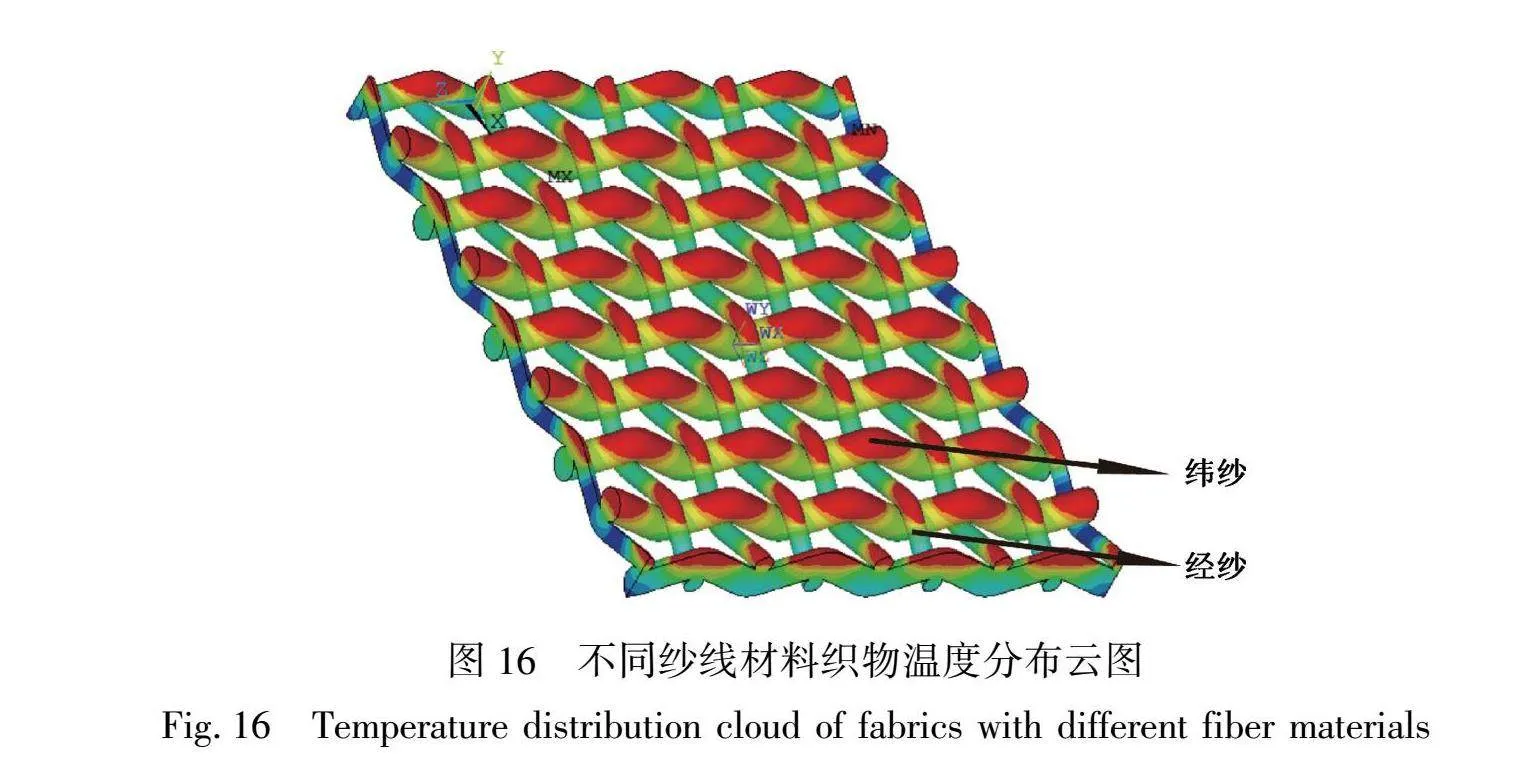
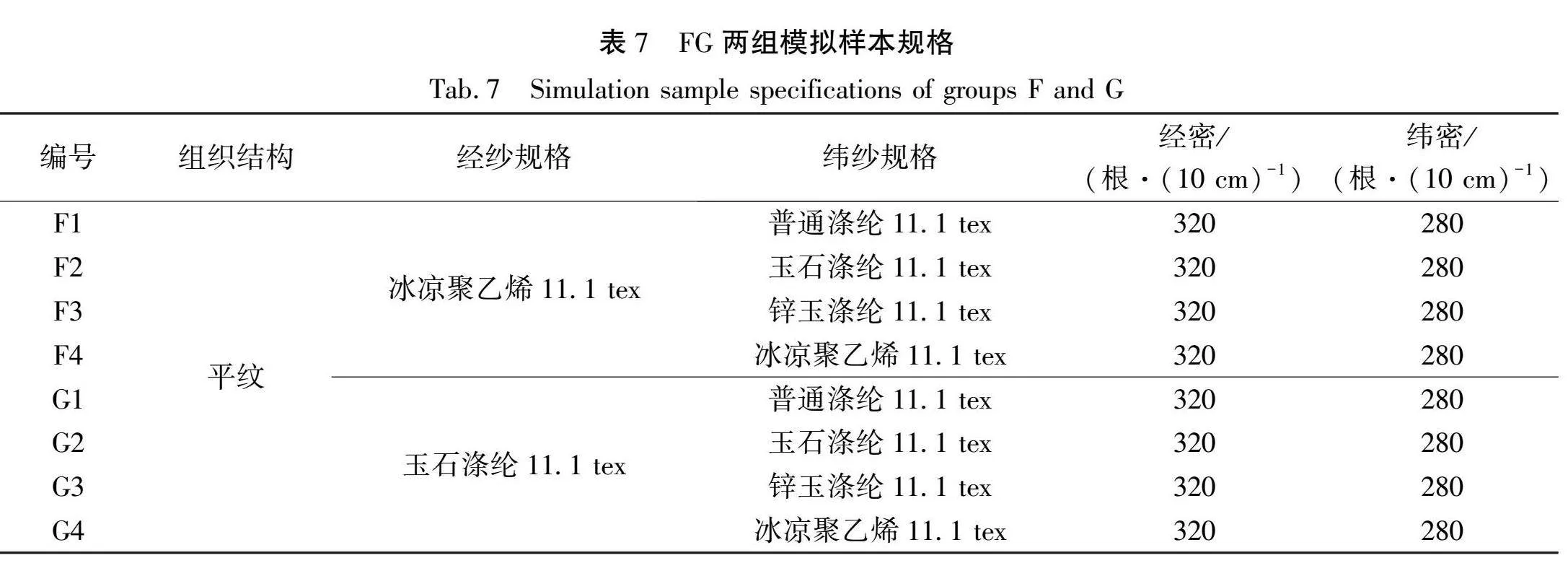
借助织物有限元导热模型，研究纱线导热系数对织物导热性能的影响。控制变量，改变织物经纬纱线材料，设计FG两组模拟样本进行有限元模拟，并进行相同上述模拟操作。两组模拟样本的规格如表7所示，不同纱线材料的织物温度分布云图如图16所示，FG两组模拟样本的蓄热系数、导热系数如图17所示。

通过设计不同经纬纱线材料的模拟样本，研究纱线导热系数对织物导热性能的影响。纱线材料的热学性质对织物的传热性能有着重要影响，对于绝大多数纱线材料而言，纤维的导热系数受内部晶格排列顺序的影响。晶格排列越有序，更有利于快速传递热振动，从而提高热量传递速度，导热系数也随之增大。因此，织物的导热性能在很大程度上取决于纱线导热系数内部晶格的有序排列，即纱线材料本身的导热性能，纱线材料的导热性能越优越，织物的热传导能力也相应增强。

4 结论

本文利用ANSYS/APDL二次开发技术对织物进行参数化建模，模拟分析不同组织、紧度和纱线材料条件下的温度分布和表面温度变化。利用有限元模型直接模拟计算织物的导热系数和蓄热系数，并进一步探究有限元模型的准确性和织物导热性能的影响因素。研究结论如下：

a） 利用ANSYS/APDL进行参数化建模适用于不同织物条件，模拟计算得到的导热系数和蓄热系数同实验测试结果的绝对误差值在4%以内，吻合度较好，模拟结果有效。

b） 不同织物组织结构对导热系数和蓄热系数影响显著，平纹织物的蓄热系数和导热系数最高，斜纹次之，缎纹最低；织物紧度越高，导热系数和蓄热系数越大，并且纱线导热系数与织物的导热系数和蓄热系数呈正相关。

参考文献：

［1］李金屿， 杨允出， 刘鸣茗. 基于结构特征的织物热传递性能预测研究进展［J］. 现代纺织技术， 202 30 （1）： 18-25.

LI Jinyu， YANG Yunchu， LIU Mingming. Research progress in the prediction of heat transfer properties of fabrics based on structural characteristics［J］. Advanced Textile Technology， 202 30 （1）： 18-25.

［2］MOKHTARI Y M， SHEIKHZADEH M， BORHANI S. Modeling the heat transfer in a PCM cooling vest［J］. The Journal of the Textile Institute， 2015， 106（9）： 1003-1012.

［3］李瑛慧， 谢春萍， 刘新金， 等. 仿真丝织物与真丝织物的热传递有限元仿真［J］. 丝绸， 2017， 54 （12）： 7-11.

LI Huiying， XIE Chunping， LIU Xinjin， et al. Finite element simulation of heat transfer on silk-like fabrics and real silk fabrics［J］. Journal of Silk， 2017， 54 （12）： 7-11.

［4］张洁， 刘新金， 谢春萍， 等. 织物结构参数对热传递性能影响的模拟分析［J］. 丝绸， 2020， 57 （2）： 13-8.

ZHANG Jie， LIU Xinjin， XIE Chunping， et al. Simulation analysis of the influence of fabric structure parameters on heat transfer properties［J］. Journal of Silk， 2020， 57（2）： 13-18.

［5］SIDDIQUI M O R， SUN D. Automated model generation of knitted fabric for thermal conductivity prediction using finite element analysis and its applications in composites［J］. Journal of Industrial Textiles， 2016， 45（5）： 1038-1061.

［6］WU X， YU P， SUN X， et al. Modeling the thermal performance of anisotropic heat conduction fabric with different structural parameters［J］. Journal of Natural Fibers， 2023， 20（1）：1-13.

［7］SIDDIQUI M O R， SUN D. Thermal analysis of conventional and performance plain woven fabrics by finite element method［J］. Journal of Industrial Textiles， 2018， 48（4）： 685-712.

［8］BARAUSKAS R， SANKAUSKAITE A， RUBEZIENE V， et al. Investigation of thermal properties of spacer fabrics with phase changing material by finite element model and experiment［J］. Textile Research Journal， 2020， 90（15/16）： 1837-1850.

［9］吴佳玥， 吴巧英. 羽绒制品热传递的有限元仿真［J］. 纺织学报， 202 43（11）： 154-162.

WU Jiayue， WU Qiaoying. Finite element simulation of heat transfer through down coat panel［J］. Journal of Textile Research， 202 43（11）： 154-162.

［10］吴茜. 织物热传递性能及其数值模拟［D］. 武汉： 武汉纺织大学， 2017： 12-44.

WU Qian. Thermal Transitivity of Textile and Its Numerical Simulation［D］. Wuhan： Wuhan Textile University， 2017： 12-44.

［11］孙玉钗， 冯勋伟， 刘超颖. 纺织品热传递有限元分析［J］. 东华大学学报（自然科学版）， 2006， 32（2）： 50-53.

SUN Yuchai， FENG Xunwei， LIU Chaoying. Application of finite element method in analysis of heat transfer through textile fabrics［J］. Journal of Donghua University， 2006， 32（2）： 50-53.

［12］吴佳佳， 唐虹. 应用ABAQUS的织物热传递有限元分析［J］. 纺织学报， 2016， 37 （9）： 37-41.

AB5fDTaM57qWmDRYhsnh6mIHFhqSgxkJsjCPQTmBq44=

WU Jiajia， TANG Hong. ABAQUS based finite element analysis of heat transfer through woven fabrics［J］. Journal of Textile Research， 2016， 37 （9）： 37-41.

YcNfpKbh4tsork8V3pR/Y3z4v3n2nR3COx9NH7HOHjE=

［13］CIMILLI S， NERGIS F B U， CANDAN C. Modeling of Heat Transfer Measurement Unit for Cotton Plain Knitted Fabric using a Finite Element Method［J］. Textile Research Journal， 2008， 78 （1）： 53-59.

［14］SIDDIQUI M O R， SUN D. Finite element analysis of thermal conductivity and thermal resistance behaviour of woven fabric［J］. Computational Materials Science， 2013， 75：45-51.

［15］李雪梅. 织物接触凉感的主客观测试评价及其影响因素研究［D］. 杭州： 浙江理工大学， 2022： 18-34.

LI Xuemei. Subjective and Objective Testing and Evaluation of Cool Feeling in Contact with Fabrics and Research on Its Influencing Factors［D］. Hangzhou： Zhejiang Sci-Tech University， 2022： 18-34.

［16］谭月敏， 徐健明， 庞文键， 等. 浅谈应用材料导热系数的测定方法［J］. 中国胶粘剂， 2023， 32 （7）： 62-68.

TAN Yuemin， XU Jianming， PANG Wenjian， et al. Discussion on measurement method of thermal conductivity of applied materials［J］. China Adhesives， 2023， 32 （7）： 62-68.

Factors influencing the thermal properties of fabrics based on ANSYS/APDL

QI Xintao HE Haonan LI Xin JIN Xiaoke MA Leilei TIAN Wei ZHU Chengyan 2

（1.College of Textile Science and Engineering （International Institute of Silk）， Zhejiang Sci-Tech University，

Hangzhou 310018， China; 2.Zhejiang Sci-Tech University Huzhou Research Institute Co.， Ltd.， Huzhou 313000， China）

Abstract：

With the growing demand for thermal comfort in textiles， there has been a heightened research focus on fabrics with excellent thermal properties. During hot summers， fabrics with excellent thermal properties can efficiently transfer the body's heat to the external environment， offering a comfortable and cool wearing experience. The thermal properties of fabrics are influenced by factors such as fabric structure， fabric tightness， yarn thermal conductivity， fiber content， and fabric post-processing. Studying these influential factors is important for the development of fabrics with excellent thermal properties.

Traditionally， developing fabrics with good thermal properties involved weaving numerous fabric samples and conducting a series of physical tests to analyze the product's thermal properties， which was time-consuming and wasteful of raw materials. Compared to traditional experimental methods， finite element analysis systems can quickly obtain indicators of fabric thermal properties such as thermal conductivity， thermal resistance， thermal effusivity， and CLO value， making fabric design more effective.

In recent years， scientists have utilized finite element software such as ANSYS and ABAQUS to simulate and predict the heat transfer performance of fabrics. This approach offers an effective means of evaluating and optimizing high-quality， low-cost fabrics. However， the CAE module simulation analysis environment has limitations that make it challenging to directly analyze fabric heat transfer performance and process data. Therefore， this study aimed to develop a system for the finite element simulation of fabric heat transfer using the improved technology of ANSYS/APDL Firstly， various fabric samples with different fabric structures， yarn materials， and warp and weft yarn combinations were woven. The parameters of the fabric structure were then measured by using microscopic imaging to create a parametric model. A three-dimensional finite element model of the "environment-fabric-skin" system was then created by using finite element software to simulate the heat transfer process and temperature distribution characteristics of the fabric during wear. This model was also utilized for calculating the thermal conductivity coefficient and thermal effusivity of the fabric. Subsequently， the C-THERM TCi thermal conductivity meter was used to measure the thermal conductivity coefficient and thermal effusivity of the fabric samples. The experimental test results were then compared with the simulation results to validate the efficacy of the model. Finally， the impact of fabric structure， fabric tightness， and yarn thermal conductivity on fabric thermal properties was investigated through finite element simulation.

Comparing the experimental test and simulation results， the absolute error of the calculated thermal conductivity coefficient and thermal effusivity from the simulation is within 4% of the experimental test results， validating the effectiveness of the model. Further exploration of the factors influencing fabric thermal properties reveals that under the same conditions， plain weave fabrics exhibit the highest thermal effusivity and thermal conductivity coefficient， followed by twill weave， with satin weave showing the lowest values. Additionally， under the same conditions， the higher the tightness of fabric is， the more its heat conductivity coefficient and effusivity will be. Similarly， as yarn thermal conductivity increases， there will also be an increase in the fabric's thermal conductivity and thermal effusivity. Hopefully， the research findings can shed a light on the parametric modeling of fabrics and the development of fabric heat transfer finite element simulation systems， and offer insights for the subsequent improvement of fabrics with favorable thermal properties.

Keywords：

finite element simulation; thermal properties; parametric modeling; thermal conductivity coefficient; thermal effusivity