核心素养视域下学生推理意识培养策略

摘要：推理意识是学生必备的数学核心素养之一，推理意识有助于学生养成讲道理、有条理的思维习惯，是形成推理能力的经验基础.在小学数学教学中，教师要引导学生经历初步的逻辑推理过程，通过创设真实的情境、加强动手操作、制造思维冲突以及重视说理思辨等策略，帮助学生形成初步的推理意识，让学生学会用数学的思维思考现实世界，使数学更具严谨性.

关键词：核心素养；推理意识；培植策略

《义务教育数学课程标准（2022年版）》指出：“数学思维主要表现为：运算能力、推理意识或推理能力.”［1］通过推理意识的培养，学生能逐步养成讲道理、有条理的思维习惯，同时形成实事求是的科学态度.

1类比迁移，培养推理意识

思维是从疑问和惊奇开始的，教学过程中，教师要创设有效的教学情境，精心合理地设计能激发学生积极思考的问题，使问题既能够结合教材中的知识，又能对学生的思维发展具有一定的引领作用，在激发学生的推理兴趣的同时，让学生能够根据已有知识，通过归纳与类比等方法推断出数学结果，从而更好地理解和掌握新知识.例如，在教学“异分母分数加减法”时，教师可以创设学生熟悉的垃圾回收情境.

纸张和废金属等是垃圾回收的主要对象，各种垃圾及其比例情况如图1所示.它们在生活垃圾中共占几分之几？

学生很容易就能列出算式310+14，接着教师就让学生想一想怎么算.有的学生就猜想把分子和分母分别相加，还有的学生认为只要把分子相加.310和14分母不同，这两种方法显然不对.这时教师就可以引导学生回忆，在整数和小数加减法中，相同的计数单位才能相加减，而分母不相同的分数就是分数单位不相同，学生很容易就推导出要先通分，把异分母分数转化成同分母分数，这样分数单位相同了，就可以直接相加减了.这就让学生体会到数的运算本质上的一致性，培养了他们的运算能力和推理意识.

在教学中，教师充分利用问题情境，引发学生的猜想，引导学生在合作探究中释疑，不但对所学知识有所领悟，而且能够从中找到方法，在新旧知识的类比过程中培养推理意识.

2动手操作，丰富推理过程

有效的推理离不开动手操作，只有加强实践操作，才能促进学生推理意识的发展.在教学中，教师应当留给学生足够的时间与空间，引导学生经历观察、猜想、推理、实验、验证等活动过程.通过观察与思考，从实践操作上升到抽象思维，引导学生参与推理的过程，帮助学生积累推理经验，学会枚举、归纳等推理方法，进而发展推理意识.

例如，在教学“三角形的内角和是180°”时，教师让学生通过量一量、算一算、折一折、拼一拼等不同的方法，寻找三角形内角的性质.活动中，有的学生利用量角器，量出三角形的三个角的度数，算出三个内角的和，发现它们的和接近180°；有的学生把三个角折到一起拼成一个平角；还有的学生把三个角撕下来拼成一个平角.通过动手操作，学生很快就推导出了三角形的内角和是180°.

操作不能只停留在单纯的动手上，更重要的是要通过操作活动撬动学生思考，教师可以适当提问.

师：动手操作是我们探究图形秘密非常好的办法，但是操作的过程总是会有一些误差，三角形的内角和确实是180°吗？同学们能不能从数学的角度进行推理？

生1：从长方形入手，一个长方形有四个直角，内角和是360°，分割成两个直角三角形，每个直角三角形的内角和是180°.

生2：有了直角三角形的内角和是180°，可以把任意一个锐角三角形沿着其中一条高剪下来，分割成两个直角三角形，然后把两个直角三角形的内角和减去180°就得到原来锐角三角形的内角和，这样得到所有的锐角三角形的内角和都是180°.

生3：用同样的推理可以得到所有的钝角三角形的内角和都是180°.

生4：三角形按角分类只能分成三类，由此得到所有三角形的内角和都是180°.

这个过程中，学生借助动手操作积累活动经验，在小组交流讨论的过程中，从特殊出发，经历从特殊到一般的推理过程.教师把更多的机会留给学生，让学生面对教师提出的问题，亲自动手操作，调动多种感官参与，引导学生从动手操作上升到抽象思维，帮助学生积累推理经验，这样学生的推理意识与推理能力就能得到很好的发展.

3制造冲突，激发推理潜能

推理意识的培养离不开数学基础知识的积累，在有了一定的基础知识积累后，学生就能通过观察、类比、联想等数学思维活动，不断地进行推理与验证.教师通过对教材的深度挖掘和合理利用，就能更好地激发学生的推理潜能，让学生的推理意识得到进一步的发展.

例如，在教学“圆的认识”一课中，教师先引导学生回忆已经学过了哪些平面图形，然后出示圆，比较它们的不同点，学生一眼就看出，以前学过的图形是由线段围成的，而圆是由曲线围成的平面图形.接着教师再出示椭圆，并提出问题“椭圆也是由曲线围成的，它是圆吗”，这就给学生制造了认知冲突.接着教师再引导学生观察椭圆的中心点到椭圆的距离不相等，而圆的中心点到圆周的距离相等，还有其他平面图形的中心点到边的距离也都不相等.这样通过观察、分析、推理，引导学生概括出圆的本质特征：一中同长.

对于新旧知识密切联系的内容，教师应该拓宽教材的深度与广度，利用学生已有的知识与经验，创设认知冲突，引导学生去观察、思考，激发学生推理潜能的发展，促进推理意识的提高.

4说理思辨，外显推理思维

教学中，教师要有意识地为学生创设数学表达的机会，让学生为自己的观点寻求证据、应对质疑，从而促进思维的清晰化、条理化，发展推理意识.教师要善于抓住推理活动的关键环节，引导学生不断经历“猜想—验证—说理”的过程，让学生在有价值的活动中，感悟推理的过程与意义.

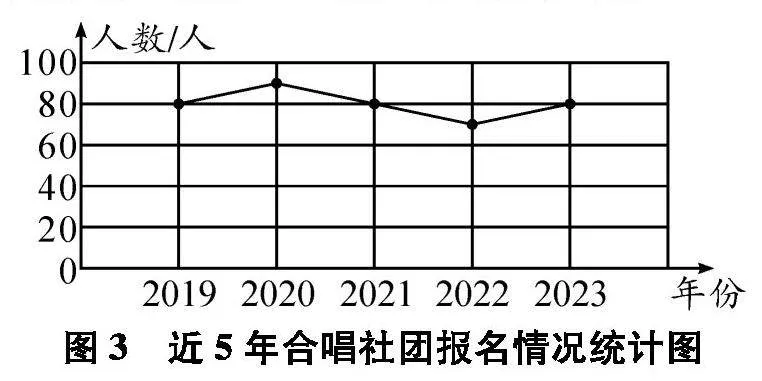
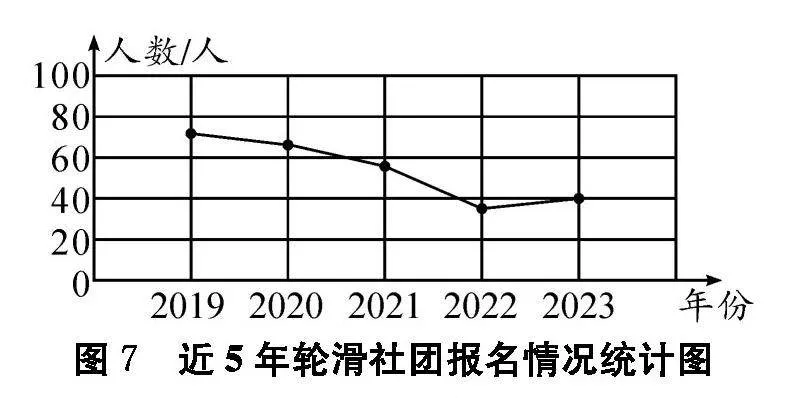
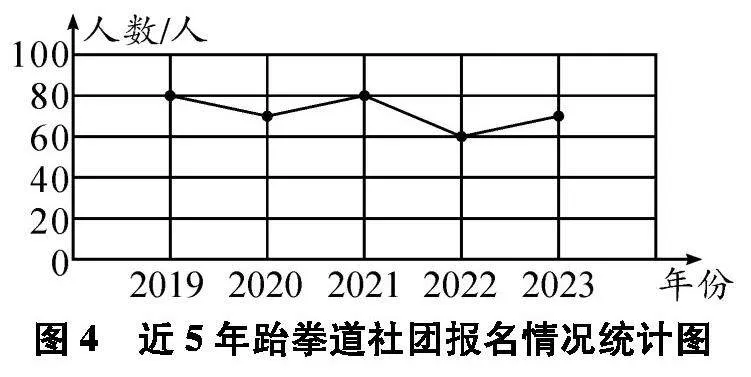
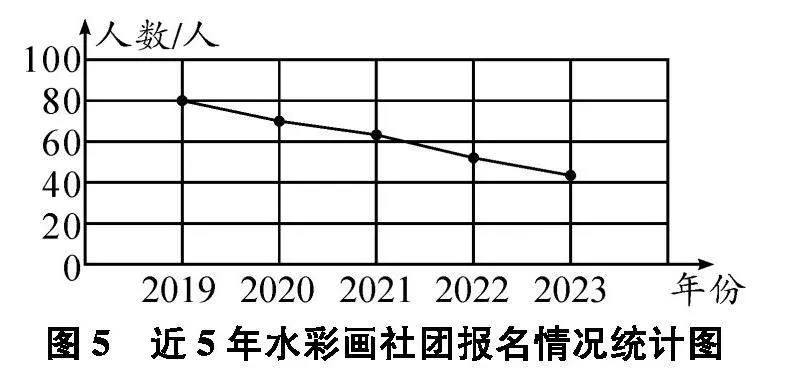
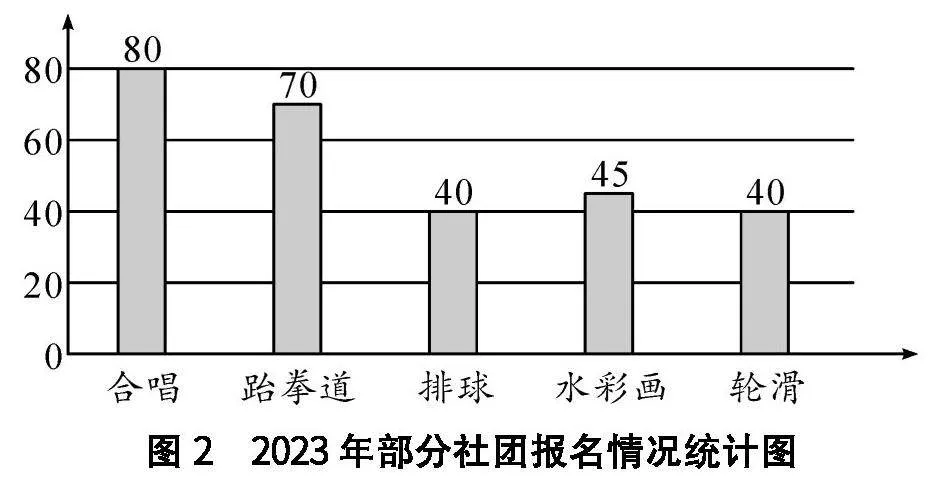
例如，在教学“折线统计图”知识点时，教师可以创设这样的问题情境.学校要精简一个社团，请学生根据图2所示的2023年部分社团报名情况统计图中的数据来选择精简一个社团，学生发现报名人数最低的排球社团和轮滑社团都是40人，无法确定精简掉哪个社团.

接着教师出示了近5年这5个社团的报名人数情况折线统计图（如图3、图4、图5、图6、图7）.根据折线统计图中曲线的变化情况，有的学生认为要精简掉轮滑社团，还有的学生认为要精简掉水彩画社团，因为它们都是呈下降趋势，而其他社团报名人数较多或呈上升趋势.这样通过条形统计图和折线统计图的对比，学生经历了猜想、辨析、反驳与验证的过程，感悟推理的方法与意义，体会数学探索和发现的乐趣.

学生说理的过程就是思考的过程，教师在教学中要给学生创设交流与讨论的机会，借助问题引领，适当地给予点拨、引导，在观察、实验、猜想与验证等数学活动中，引导学生逐步养成清晰地表达自己的思考过程与思考结果的习惯，帮助学生学会有条理地表达，有逻辑地思考，让学生在不断思辨中掌握数学知识本质.5结语

推理意识决定了学生用数学思维思考现实世界的水平，学习数学在某种意义上就是学习推理.发展学生的推理意识，应该贯穿小学数学教学的全过程.教学过程中，教师要引导学生“大胆猜想，小心求证”，做到言之有理、言之有据，这是数学推理活动的要求，也体现了数学学科的学习特点.

参考文献

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022.