具身学习：让学生在峰值体验中发展思维

摘要：具身学习的探究活动，可以放大学生的多感官体验，调动学生视觉、听觉、触觉等感官系统，让学生自主自发地参与数学探究，在峰值体验中发展数学思维和数学素养.本文以“认识垂线”教学为例，对具身学习的相关问题作出具体阐述.

关键词：具身学习；峰值体验；认识垂线

《义务教育数学课程标准（2022年版）》倡导学生自主自发地参与数学实践活动，让学生亲历知识的发现、发展、建构和运用的过程，体会数学思想方法.［1］当前小学数学教学实践中，存在诸多教与学的失衡现象，如围观式、旁观式探讨、做思分离现象严重等.基于上述现象，笔者通过设计具身学习的探究活动，放大学生的多感官体验，努力调动学生视觉、听觉、触觉等感官系统，让学生自主自发地参与数学探究，从而在峰值体验中发展数学思维和数学素养.

1教学过程

教学环节1：在观察中感知垂直.

直接导入：本节课我们研究“两条直线间的位置关系”.

问题1如图1所示，方框内有一条直线，再画一条直线使得两条直线相交.

学生自主尝试，教师来回巡视，并收集学生成果.

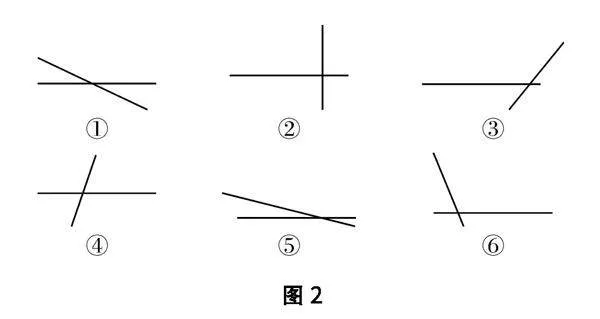
问题2如图2所示，这些图形的两条直线都相交，它们有什么共同特征，又有什么不同之处？

它们都有一个交点、4个角，但4个角的大小不同.

问题3这些图形中，两直线相交的4个角，最特殊的是哪一个？为什么？

图2中②最特殊，因为这里的4个角均为直角.

问题4你的作品有没有呈现这种特殊情况？谁能在黑板上演示这种特殊的相交？

学生板演，并用三角尺上的直角验证后标注直角符号.

总结：这种相交所成角都为直角的两条直线的位置关系是互相垂直.

【设计意图】学生都是富有生命活力的个体，开放的活动情境极易激起他们的兴趣和好奇.教师用开放性的问题情境巧妙导入，使学生在多感官参与中逐步看清互相垂直的特征与要素.教师引导学生观察4个角都是直角的特殊相交，实现思维图象与实际图象的沟通，使得原本模糊的概念变得清晰起来，使概念基本模型得到切实建构.

教学环节2：在实践中体验垂直.

探究活动1：图3是实验研究任务单，请以小组为单位积极研究，之后汇报研究成果.

学生充分探讨后积极汇报.组1：从羊村朝着公路作线段来表示直路，画法很多，但为了加快材料运输，肯定需要路程最短，这样才能运输用时最少.因此经过量和比，发现与公路垂直的线段最短.组2：本组的方法类似于组1.如图4所示，纸条表示直路，于羊村这一点固定住纸条的一段，并一直旋转纸条后发现只有垂直这种情况可以碰到公路.组3：我们也是通过测量和比较的方法发现羊村至公路所画线段中互相垂直的这一条线段是最短的.

总结：数学上羊村这个点用点P表示，公路所在直线用l表示，点P到直线l的这条垂直线段的长称为点到直线的距离.

提问：点到直线的距离与前面所研究的两点间的距离有什么区别？

前者是垂直线段的长度，后者是连接两点间线段的长度.

评析：实践操作作为一种多感官参与的数学活动，有利于知识的自然建构.教师以问题为载体，以实践为方式，引导学生在动手操作中测量、比较，切实体验数学概念的产生和发展，在峰值体验中实现概念的正向生长.

教学环节3：在交流中厘清本质.

探究活动2：为了更加清楚地了解互相垂直的特征和与之相关的知识，一起来探究图5所示的学习单1.

师：谁愿意先汇报？

生1：对于问题①，我觉得两条直线相交成直角，则它们互相垂直.我圈注的重点是“相交成直角”，目的在于强调“唯有相交构成直角才是互相垂直”.

师：那么问题②呢？

生2：我觉得直线a是直线b的垂线.

生3：完整地说，不仅如此，直线b也是直线a的垂线.

师：那直接说“直线a是垂线”，正确吗？

生4：错误，垂线并非一条直线，而是两直线的位置关系，因此概念中的“互相垂直”也很重要.

师：问题③呢？

生5：两条直线的交点即为垂足.

师：那图6中这个交点也是垂足吗？

生6：不对，图6中的两条直线没有互相垂直，因此没有垂线与垂足.

评析：深度对话作为一种交往互动的有效方式，可以更好地帮助学生厘清知识本质，高效建构.教师以学习单驱动学生自主探究、合作学习，引导学生在深度对话中质疑、辨析和澄清，最终达成共识，使学生实现对概念本质的深刻理解.

教学环节4：在游戏中创造垂直.

探究活动3：自主完成图7所示的学习单2.

学生自主尝试.教师巡视并收集图8所示的成果.

提问：大家的折法各不相同，但折痕却都互相垂直，为什么？

追问：在折的过程中，哪一条折痕更关键？

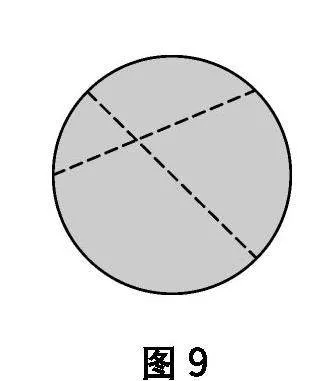
再追问：图9是老师所折的图形，现在老师需要你们的帮助，如何才能让它变成符合要求的作品？

评析：适时且有效的应用可以强化学生的经验，实现对概念的深刻理解.教师适时抛出折纸游戏，让学生自主创造“互相垂直”，以强化对现象的认知体验.学生在动手操作、尝试验证和概括总结中有效调用已有认知经验，积累并生成新的思维经验，使得概念得到自然建构的同时实现数学素养与能力提升.

2教学思考

2.1感中悟——多感官的通道整合

为了帮助学生深度理解概念，教师需从具体学情出发设计适切且丰富的体验活动，充分调动学生多感官参与活动，在具身学习中探寻个体经验和数学本质的关联，使高质量的探究真实发展，让数学思维自然发展.教师在课始就设计生动活泼的具身活动，通过看、画、比、说等具身活动，让学生全身心参与到垂线的感知中，在具身体验中建构概念的基本模型.

2.2导中建——多维度的自主参与

一手包揽的具身学习常常使学生产生被操纵感和距离感，从而难以达到应有的教学效果.具身学习的驱动力在于激发学生的内驱力，因此教师需定位好自身的角色，以引导者和合作者的身份助力体验活动的展开，让学生以主角的身份开展体验活动，发挥自身的智慧，舒展自身的灵气，提高具身学习的成就感，发展数学核心素养.教师基于学生立场设计学习单，给足了学生创造的空间，让学生主动参与创造活动，在具身体验中形成创新见解，然后共享再生，最后形成对知识更加深刻、全面和丰厚的理解，自然发展数学思维.

总之，行为认知是建立在学生的经验认知基础上的，是对经验认知的一种推进和发展.［2］具身学习可以让学生用身体思维学习，让学生从离身旁观者转型为具身构建者，有效地发挥数学活动的价值，同时，让学生建立真实而有用的数学知识和能力，构建数学学科实践的峰值体验，发展学生的数学素养.

参考文献

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022.

［2］陈红苗.具身学习 让数学学习更生动［J］.黑龙江教育（教育与教学），2022（2）：60-61.