联系，让学习触及数学本质

摘要：数学学科知识是一个不可分割的整体，各个知识间有着千丝万缕的联系.本文以“用正比例解决问题”教学为例，运用联系的观点，揭开知识和方法背后的联系，让深度学习自然发生，让学习触及数学本质.

关键词：联系；数学学习；正比例

数学学科知识系统性强，其内部知识组成了一个相互联系的整体，各个知识间有着千丝万缕的联系，即“结构”.教师引导学生建立联系，可以让数学深度学习自然发生，可以让学习触及数学本质.“数学基础知识的教学，不应求全，而应求联”，教师要基于数学知识的整体化，用联系的观点指导教学，这样才能将知识结构有效转化为认知结构，让学生的浅层思考走向深度思考，使数学学习触及数学本质.［1］本文以“用正比例解决问题”教学为例，谈谈如何运用联系的观点引领数学深度学习，让数学学习触及数学本质.

1简析教学过程

环节1：链接旧知，降难激趣.

问题1一汽车2小时行驶了120千米，从A地匀速行驶到B地共用5小时，试求出A、B两地的距离.

120÷2=60（km/h），60×5=300（km）.

追问这个问题是已学的什么问题？

归一问题.

总结：事实上，这个问题看似熟悉，实则是今天所要学习的新内容，让我们一起来体验“旧题新做”，看看是否别有一番滋味.

环节2：链接方法，深度思考.

问题2请自主尝试探寻其他解法.

学生自主思考后汇报思路.方法一，设A、B两地相距x千米，因为两段行程中速度是不变的，则可列式120∶2=x∶5.方法二，设A、B两地相距x千米，因为速度一定即“行驶120千米的路程∶时间”与“行驶x千米的路程∶时间”相等，则可列式1202=x5.

方法三，设A、B两地相距x千米，因为两段路程速度相等，则可列方程120÷2=x÷5.

问题3这三种做法，有何相同之处，又有何不同之处？

教师课件呈现图1，学生思考后给出如下观点.相同点在于“根据速度相等建立关系式”.不同点在于“3个等式分别为比、分数和除法的形式，但可相互转化”，且从本质上来看，120∶2=x∶5和1202=x5都是比例，差异仅在书写的形式上而已.

120∶2=x∶51202=x5120÷2=x÷5

问题4有没有其他解题方法？

方法四，设A、B两地相距x千米，则可列式2∶5=120∶x.

追问方法四合理吗.等式的建立有什么前提.

合理.速度一定.

问题5上述四种方法哪些是新方法，是通过什么比例解决问题的？

方法一、方法二和方法四都是新方法，使用正比例关系解决问题.随之教师适时板书.

环节3：深度探究，厘清本质.

问题6在用正比例解决问题时，关键之处是什么？

不变量.

问题7本题抓住这个“不变量”，还能再写出什么比例式？

2∶120=5∶x，因为等式两边都表示的是行驶1千米所需时间，因此等式两边相等.速度一定时，行驶1千米所需时间相等，时间是不变量.

问题8把握“不变量”可以用正比例解决问题，并列出各种比例式，请试着阐述正比例解决问题的步骤.

120∶2=x∶5.①根据不变量判断题中哪两种相关联的量成正比例；②找出两组相对应的数，并设出未知数，列出比例；③列出比例式.

环节4：有效辨析，内化新知.

问题9王阿姨家7月份用水量为8吨，需缴纳水费28元.若李大爷7月份缴纳水费42元，则李大爷7月份用水量是多少？请在草稿纸上解答.

学生自主完成，教师来回巡视，并搜集到典型作品，即28∶8=42∶x.

问题10用正比例解决问题时有哪些注意点？

①关联的量是否成正比例关系；②不能忽视设未知数的环境；③等式两边数量关系需一致，不变量需相同.

环节5：回顾反思，深化理解.

问题11回顾之前汽车行驶问题的算术法和比例法这两种解法，有何相同之处，又有何不同之处？

相同之处在于速度都不变，且一个是算术法解答，另一个是比例法解答；不同之处在于算术法需先求出不变量再解答，而比例法则是根据数量关系列出一个比例式来表示这个不变量.

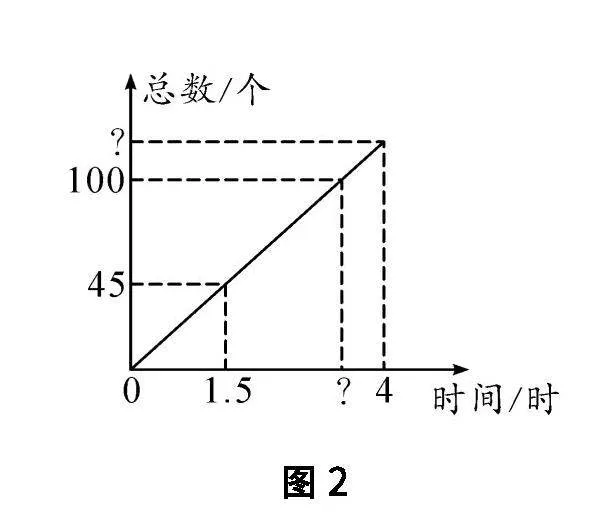
问题12王师傅正在连夜加工一批零件，图2为工作时长与加工零件个数的关系图，请试着利用比例知识进行解答：当加工零件100个时，王师傅工作了多久；当王师傅工作4个小时，加工了多少零件？

2教学思考

2.1新旧链接找联系，激发思维活力

学生对新知的学习产生兴趣是有意义学习发生的先决条件，情感是学生兴趣的核心成分.用正比例解决问题，事实上就是已学的“归一问题”和“归总问题”.显然该阶段的学生已经掌握了这类问题的解法，那么本节课学习的意义是什么，如何推进才能达到激趣引思之效，这些都需要教师深入思考和巧妙设计.本节课中，教师应牢牢把握新旧知识间的联系，并以此为入口准确切入，在学生解决旧题之后，抛出问题“还能用其他方法解答吗.”充分调动学生进一步探究的兴趣，使他们产生了积极的学习心向，使深度思考自然发生.

2.2由表及里找联系，引发深度思考

以联系为途径，可以帮助学生实现知识和方法的重构，形成一个更强的结构系统.在“用正比例解决问题”的教学

中，教师以问题引导学生拾级而上地探究，组织学生多次对比算术法和比例法这两种解法的相同之处和不同之处，由表及里地体会两种解法在本质上的趋同，使学生对正比例解决问题的理解从模糊到清晰，增强学生的数学理解，一步步地将比例法纳入到一个更强的“大结构”之中，实现更高层次的概括.

2.3强化沟通和比较，探明数学本质

在本节课学习的过程中，学生依旧无法理解“既然已经掌握了解法，为什么还要多此一举地掌握正比例知识解决问题的方法”.因此，就本节课的教学而言，不仅仅为了方法的习得，更重要的是使学生去沟通和比较方法间的异同，在自觉反思中体验比例法解决问题的优势和独特作用，促进学生在理解算理基础上优化方法、凝练思维.教学的过程中，教师关注两种方法的沟通与比较，让学生去思考、去探究、去发现，探索得到两种方法的异同点，体会比例法解决问题的优越性，从而为后续代数思维和函数思想的领悟打下坚实的基础.

3结语

纵观上述教学构思与学法指导，“用正比例解决问题”的教学并没有急于求成.教师通过现实的、朴素的素材建立联系，引导学生去思考、去探究、去交流、去感知、去体验、去感悟，促进学生思维的自然跃升，提高学生的解决问题能力，发展学生数学核心素养.因为联系，让数学学习触及数学本质；因为联系，让数学课堂走向深处.

参考文献

［1］袁敬丰，张晓霞.联系：让数学学习真正发生——以“约分”教学为例［J］.教育研究与评论（小学教育教学），2019（5）：54-57.