SOLO分类理论下的小学数学课堂教学优化研究

摘要：SOLO分类理论对于小学数学教学具有重要的指导意义.本文对SOLO分类理论进行了概述，阐述了其对于小学教学的指导意义，结合教学实践提出SOLO分类理论下的小学数学课堂教学优化策略.

关键词：小学数学；SOLO分类理论；课堂教学优化

1SOLO分类理论概述

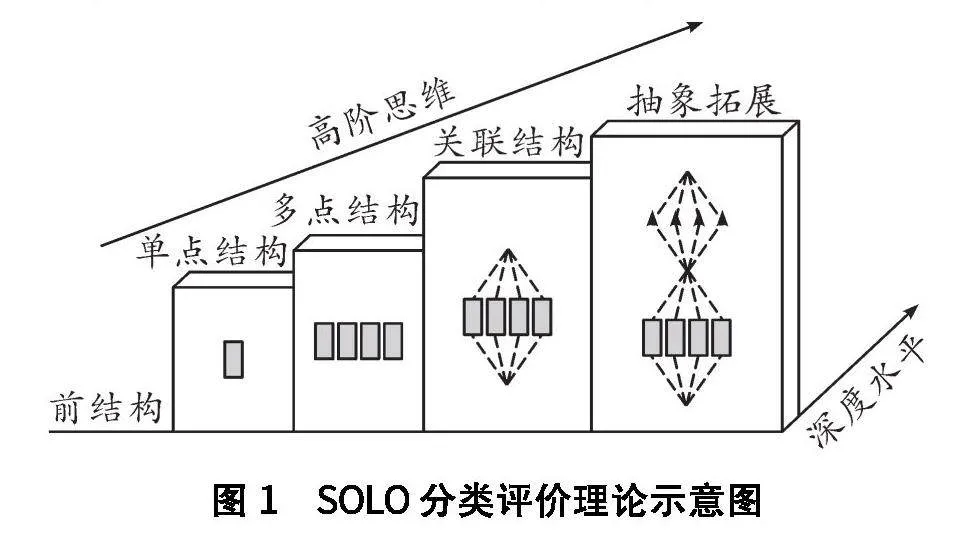
SOLO（Structure of the Observed Learning Outcome）分类理论是一种用于评估学生学习成果的理论.它旨在描述和分类学生在学习过程中所表现出的不同层次的理解和能力.SOLO分类理论将学生的学习成果分为以下五个层次（如图1）：①前结构层次.学生在这一层次没有形成有意义的理解，无法解决或回答基本的问题.②单点结构层次.学生能够理解和使用单一的知识点或单一的技能，可以回答基本的问题，但不能将知识点联系起来或应用到新的情境中.③多点结构层次.学生能够理解和使用多个独立的知识点，但无法获取这些知识点之间的内在联系，可以记住和列举多个要点，但不能将它们综合起来.④关联结构层次.学生能够将多个知识点联系起来，形成一个有意义的整体，能够理解知识点之间的关系，并能够在新的情境中解释、应用这些知识.⑤抽象扩展层次.学生不仅能将知识点联系起来，还能超越具体情境，抽象出更高层次的概念和原理.学生能够创造性地应用知识，提出新的理论或解决复杂问题.

2SOLO分类理论对于教学的指导意义

2.1制定教学目标

根据SOLO分类理论，教师可以设定不同层次的教学目标.例如，低年级学生主要处于单点结构和多点结构层次，教师在教学时帮助他们掌握基础的数学概念和技能；对于高年级学生，教师可以逐步引导他们达到关联结构和抽象拓展层次，培养他们的数学思维能力和问题解决能力.

2.2设计教学活动

SOLO分类理论可以帮助教师设计层次分明的教学活动，从而满足不同学生的学习需求.［1］例如，针对处于单点结构和多点结构层次的学生，教师可以设计一些基础练习和重复性活动，帮助学生巩固基本概念；针对处于关联结构层次的学生，教师可以设计一些需要综合运用多个知识点的问题，促进学生的深度理解；针对处于抽象拓展层次的学生，教师可以设计一些开放性问题和探究性活动，鼓励学生进行创造性思考和应用.

2.3采取个性化教学

每个学生的理解能力和学习进度不同，SOLO分类理论为教师提供了一个框架，可以根据学生的实际情况进行个性化教学.例如，对于理解较浅的学生，教师可以给予更多的基础指导和练习，巩固他们的知识；对于理解较深的学生，教师可以提供更具挑战性的任务和问题，激发他们的潜力.

2.4进行反馈与评估

利用SOLO分类理论，教师可以提供更具针对性的反馈.例如，当学生的解答仅处于单点结构层次时，教师可以引导他们思考如何将不同的知识点联系起来；当学生已经达到关联结构层次时，教师可以让他们进一步拓展，促使他们达到更高层次结构.

3SOLO分类理论下的小学数学课堂教学优化策略

3.1立足学生思维层次，开展针对性教学

教师根据SOLO分类理论，针对不同思维层次的学生，设计和实施对应的教学活动路径（如图2）.

3.1.1前结构

教学目标：针对知识没有理解或存在误解的学生，目标是引导学生建立基本的数学概念.

教学策略：提供直观的材料和简单的示范，引发学生的兴趣和初步理解.

教学案例：在认识“数的概念”教学中，教师使用实物（玩具、小石子）进行数数活动，带领学生一起数数，逐个点数并大声说出数字，帮助学生初步了解“数量”的概念.

3.1.2单点结构

教学目标：针对只理解一个方面知识点的学生，目标是帮助学生掌握单一的数学概念或技能.

教学策略：通过反复练习和简单应用，巩固学生对单一知识点的理解.

教学案例：在“加法”教学中，教师在黑板上写出加法算式，带领学生计算，使用图形或手指辅助，确保学生能准确地进行简单的加法运算.

3.1.3多点结构

教学目标：针对理解多个孤立知识点的学生，目标是帮助学生掌握多个相关的数学概念.

教学策略：提供多个独立的练习，帮助学生分别掌握各个知识点.

教学案例：在“加法和减法”教学中，教师分别讲解加法和减法的计算方法，让学生完成一系列相关练习，引导学生进行加法和减法运算.

3.1.4关联结构

教学目标：针对能够将多个知识点联系起来，形成系统性理解的学生，目标是帮助学生综合运用所学知识.

教学策略：设计综合性问题或任务，要求学生将不同的知识点联系起来解决问题.

案例：在“用加减法解决实际生活中的数学问题”教学中，教师设置购物的情境.学生需要综合运用加法和减法，理解购物中找零的过程.

3.1.5抽象拓展

教学目标：针对能够将知识应用于新的情境，进行抽象和概括的学生，目标是培养学生的数学思维能力和创新能力.

教学策略：提供开放性问题和探究性活动，鼓励学生进行创造性思考和应用.

案例：在“数学项目探究”教学中，教师设计一个简单的数学项目，如“调查班级同学的生日月份并绘制图表”，引导学生收集数据（每个同学的生日月份），然后绘制对应柱状图或饼图，分析哪个月份生日最多.学生在收集、整理、分析数据的过程中，应用所学的统计知识，进行抽象和概括，并解释图表中的信息.

3.2运用SOLO分类理论，加工和优化教材内容

在小学数学教材的设计中，教师运用SOLO分类理论可以有效地推动学生的思维层次向高阶发展，以苏教版《义务教育教科书数学三年级上册》中“分数的初步认识”教学为例，说明如何促进学生思维水平的提高.

（1）前结构层次.教师展示分数的概念之前，可以先进行预备知识的激活，如复习整数和小数的概念，确保学生具备基本的数感.

（2）单点结构层次.教师讲解分数的定义，如“分数是表示一个整体被分成若干部分后的某一部分”，并通过直观的图示（饼图）帮助学生理解.例如，教师给出一个饼图，将其分成4份，将其中的1份涂色，解释“14”的含义.

（3）多点结构层次.在学生理解基本定义后，教师可以提供多种类型的分数图示和实际例子，帮助学生识别和表示不同的分数.例如，教师给出多个图示，让学生识别并写出对应的分数，教师还可以列举切蛋糕、分糖果等生活中的例子，让学生用分数表示这些情境.

（4）关联结构层次.教师引导学生将分数与其他数学概念联系起来，如分数与小数的关系、分数的比较与运算.例如，教师可以让学生将12与0.5进行比较，并解释为什么它们相等.除此以外，通过解决“如果有一块蛋糕切成8份，吃了其中的3份，还剩这块蛋糕的几分之几”这类实际问题，帮助学生感受分数在实际生活中的运用.

（5）抽象拓展层次.在学生已经能够关联和运用分数概念后，教师可以设计更具挑战性和创造性的任务，促使学生进行更深层次的思考和应用.例如，教师设计一个项目，让学生调查生活中分数的应用并制作报告，还可以引导学生进行开放性问题的探讨，在探索过程中推动思维层次的进一步发展.

3.3结合SOLO分类理论设计小学数学试题

基于SOLO分类理论设计小学数学试题应包括以下原则：①符合学生认知发展阶段.设计的试题应适合小学生的认知能力和发展水平，确保学生能够理解和解决问题.具体到教学中来看，题目的难度应逐步增加，从简单的识记和理解到复杂的应用和推理.例如，从简单的加减法算式，到需要综合应用多种运算解决实际问题.②包含多层次学习目标.设计的试题应涵盖不同层次的学习目标，反映从基础知识到高层次思维的各个阶段.③提供反馈和反思机会.设计的试题应有助于教师评估学生的学习进度，并为学生提供反馈，促进其反思和改进.此外，教师可以设置开放性问题，允许学生展示其思维过程，通过学生的回答了解其理解深度，并提供有针对性的反馈.

参考文献

［1］莫与谈.SOLO分类评价理论下小学高年级数学教学的实践［J］.中小学数学（小学版），2021（9）：13-14.