小心“陷阱”

解答规律探索题时，有些同学由于忽视题设中的隐含条件最后功亏一篑，因此，解决此类问题时，要仔细斟酌，谨防“陷阱”．

例1 如图1，将方框在月历表格中移动，计算方框中9个数的和，下面有4个计算结果：100，171，189，216.其中计算结果正确的有（ ）．

A.1个 B.2个

C.3个 D.4个

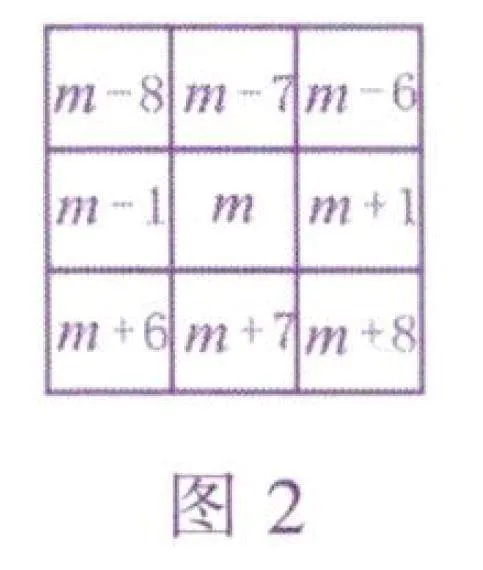
解析：不难发现，月历表中隐含着两个规律：一是左右相邻的两个数，右边的数比左边的数大1，二是上下相邻的两个数，上边的数比下边的数小7．不妨设方框正中心的数为m，则方框中其他方格中的数都可以用含m的式子表示出来，如图2．因为m-8+m -7 +m -6+m -1+m +m+1+m +6 +m +7 +m +8=9m，所以方框中的9个数的和是方框正中心数的9倍，也就是说，方框中的9个数的和必须是9的倍数.100不是9的倍数，而171=9×19，189=9×21，216=9×24，到此，部分同学认为后面3个结果计算正确，而错选C．实际上，认真观察图1中的月历表，不难发现方框正中心的数不能为21和24．所以这4个计算结果中仅有1个是正确的，故正确答案为A．

例2 晓敏同学上第1层楼用时m秒，然后每多上1层楼将多用n秒，那么晓敏同学从操场回到5楼教室，仅上楼所用的时间为____秒．

解析：少数同学不假思索地认为：上第1层楼用时m秒，上第2层楼用时（m+n）秒，上第3层楼用时（m+2n）秒……上第5层楼用时（m+4n）秒，于是得到晓敏同学仅上楼所用的时间（单位：秒）为m+（m+n）+（m+2n）+…+（m+4n）=5m+10n.显然解答是错误的，因为我们到n楼是表示到达第n层楼的楼底，这样，到2楼就是上了1层楼，到5楼就是上了4层楼，所以晓敏同学仅上楼所用的时间（单位：秒）为m+（m+n）+（m+2n）+（m+3n）=4m+6n.

试一试

已知：2+2/3=22×2/3，3+3/8=32×3/8，4+4/15=42×4/15，…，观察其规律，用含n的式子表示第n个等式是____．

参考答案：

n+1+（n+1/（n+1）2-1）=（n+1）2·（n+1/（n+1）2-1）