经历抽象过程 发展推理能力

有人问我。为什么要学习数学？其实，简单地说就是学会用数学的眼光观察现实世界、用数学的思维思考现实世界、用数学的语言表达现实世界．

从数到式，是数学发展的重要阶段，学习代数式、整式的加减运算，需要深刻领会整式形成的过程，在规律的把握中，体会整式恒等变形的内在规律．

一、发展符号意识，提升抽象能力

实际问题中包含着一些数量和数量关系，可以用数学式子简明地表达，例如：一个长方形的长和宽分别是a，b，这个长方形的周长L是多少？由长方形的周长公式，可得周长L=2（a+b），对于2（a+b）这个式子，显然是用运算符号把数或表示数的字母连接起来的，我们称这样的式子为代数式．

在解决一些数学问题与实际问题时，往往需要先把问题中的数量关系用含有数、字母和运算符号的式子表示出来，也就是要列代数式．而同一个代数式可以表示不同实际问题中的数量或数量关系．例如，代数式100-2x可以表示哪些不同实际问题中的数量或数量关系？我们可以这样思考：如果x元是一件某商品的价格．那么式子100-2x表示用100元买2件该商品还剩的钱数：如果。表示每天读书的页数，那么式子100-2x可以表示1本100页的书读了2天后剩余的页数．因此，我们要在现实情境中理解符号表示的意义，解释代数式的具体含义．

二、解决实际问题，提升推理能为

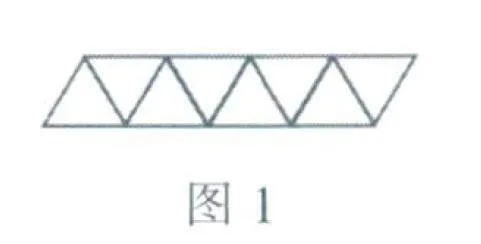
我们来看这样一个问题：用火柴棍摆成一排由三角形组成的图形（如图1所示）．如果图形中摆出了n个三角形，那么需要多少根火柴棍？

下面是几位同学的答案，我们一起来分析他们思考的过程．

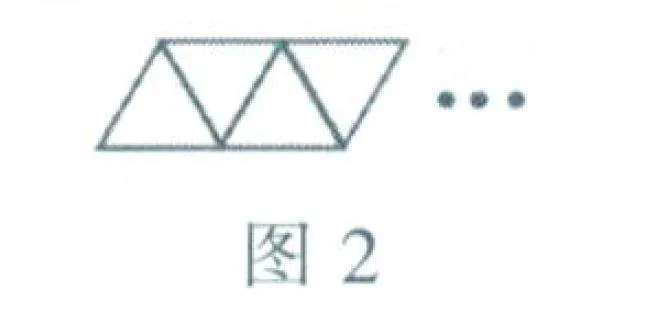
A同学：如下页图2所示，整个图案由上层、中间层和底层三部分组成，当图形中摆出了几个三角形时，上层与底层的火柴棍的根数之和就是三角形的总个数n，而中间层的火柴棍的根数是三角形的总个数n加1．所以，共需要（n+n+1）根火柴棍．

B同学：如下页图2，摆出1个三角形，一共需要火柴棍1+2=3（根）；摆出2个三角形，一共需要火柴棍1+2×2=5（根）；摆出3个三角形，一共需要火柴棍1+2×3=7（根）……所以，如果摆出几个三角形，一共需要（1+2n）根火柴棍．

C同学：如图2，当摆出1个三角形时，需要3根火柴棍；当摆出2个三角形时，需要火柴棍3×2=6（根），但是，有一边是重合的，所以，要拿走火柴棍2-1=1（根），也就是一共用了火柴棍3×2-（2-1）=5（根）；当摆出3个三角形时，需要火柴棍3×3=9（根），但是，有两边是重合的，所以，要拿走火柴棍3-1=2（根），也就是一共用了火柴棍3×3-（3-1）=7（根）……当摆出几个三角形时，需要[3n-（n-1）]根火柴棍．

D同学：当摆出1个三角形时，需要3根火柴棍；当摆出2个三角形时，在3根的基础上加上2根火柴棍，即3+2=5（根）；当摆出3个三角形时，在3根的基础上加上2×2根火柴棍，即3+2×2=7（根）……因此，当摆出n个三角形时，需要[3+2（n-1）]根火柴棍．

同样的问题，为什么会有不同的答案呢？谁的答案才是正确的呢？接下来我们进行解释说明．

考虑到字母n取值的任意性，我们来验证一下（参见表1）．

从表1中我们可以发现，无论n取什么值，四个整式的结果总是相同的，那么，四位同学的答案是否都正确呢？也就是说，四位同学所得的式子是否都相等呢？

这是我们的猜想！而且这个猜想是合理的（起码就我们验证的数字来说，是对的）．可以发现，在四个式子中，1+2n是最简单的，计算起来也最简捷．

猜想1：n+n+1=2n+1．

思考过程：我们可以将这个多项式中相同的项“加”在一起，即n+n=2n，因而，n+n+1=2n+1是有道理的．

猜想2：3n-（n-1）=2n+1．

思考过程：如果这个等式成立，那么必然有n-（n-1）=1，也就是说，-（n-1）等于-n+1．换句话说，去掉括号前的负号和括号，括号内的各项的符号都要改变．

猜想3：2（n-1）+3=2n+1．

思考过程：如果这个等式成立，那么必然有2（n-1）=2n-2，也就是说，去掉括号，括号内的各项都要同时乘括号前的数．

通过解决上述问题，分析三个猜想，我们实际上“发现”了去括号法则和合并同类项法则——尽管这两个法则是规定！在解决上面问题的过程中，我们发现，此规定是合理的，否则，就会出问题．

试一试

1．（2024年贵州）计算2a+3a的结果，正确的是（ ）．

A.5a B.6a

C.5a2 D.6a2

2．（2024年苏州）若a=b+2，则（b-a）2=____.

参考答案：

1.A

2.4