基于改进分布估计算法的能耗最优AUV路径规划算法与仿真研究

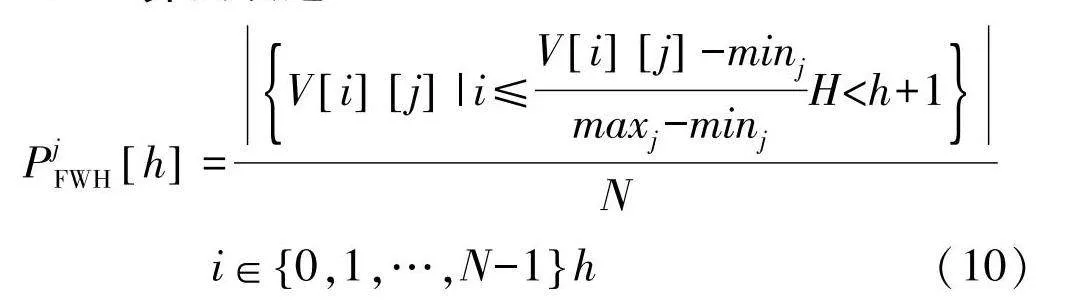
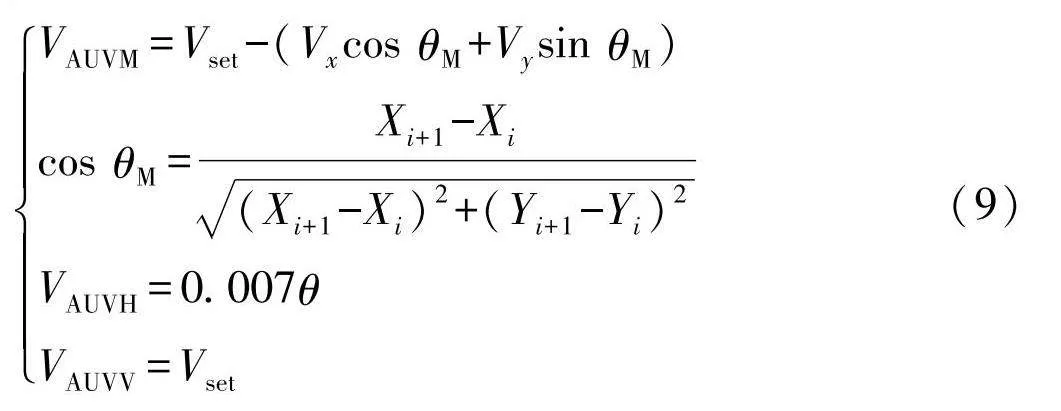
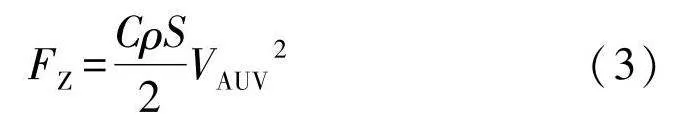
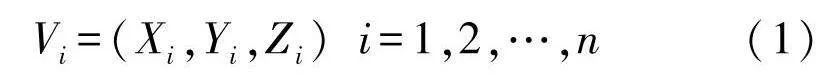
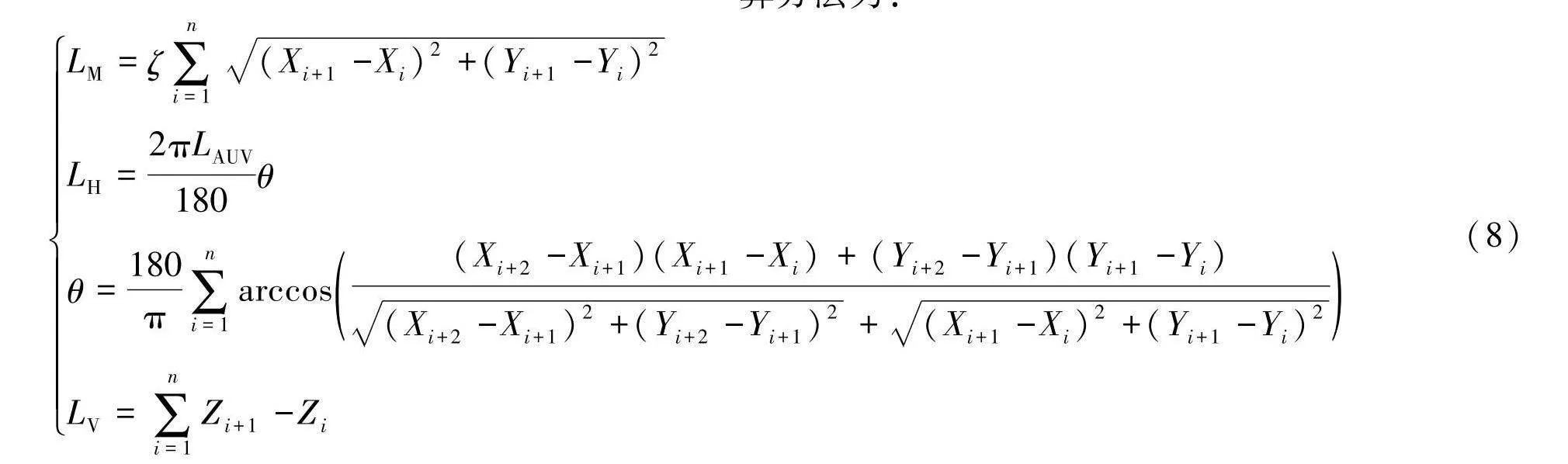
摘"要： 针对经典基于等宽度直方图的分布估计算法（FWH）在解决自主水下机器人（AUV）路径规划问题中易陷入局部极值、计算精度不高等问题，提出一种受粒子群优化算法启发的改进分布估计算法.通过将FWH与粒子群优化算法中优势个体的部分筛选机制相结合的方法，组成双重优势个体产生方法，提高AUV路径规划最优路径的精度，增加收敛速度.在水下数字高程模型环境中对经典分布估计算法、PSO算法、A*算法以及改进后的算法进行性能评估.仿真结果表明，相比于改进前的算法，新的算法计算出的能耗值减少24.9%，有效增加计算精度，避免陷入局部极值，提高效率.

关键词： 分布估计算法；路径规划；能耗最优；粒子群优化算法；水下数字高程模型

中图分类号：TP24"""文献标志码：A""""""文章编号：1673-4807（2024）04-058-07

Research on optimal AUV path planning algorithm and simulation of energyconsumption based on improved estimation of distribution algorithm

DAI Xiaoqiang1， XU Hewei1， WANG Ying2， SUN Xiaotian1， SHANG Le1

（1.College of Automation， Jiangsu University of Science and Technology， Zhenjiang 212100， China）

（2.School of Computer， Jiangsu University of Science and Technology， Zhenjiang 212100， China）

Abstract：In order to solve the problem that the classical distribution estimation algorithm based on equal width histogram （FWH） is easy to fall into local extremum and the calculation accuracy is not high in the path planning problem of autonomous underwater vehicle （AUV）， an improved distribution estimation algorithm inspired by particle swarm optimization （PSO） algorithm is proposed. By combining FWH with the partial screening mechanism of dominant individuals in particle swarm optimization algorithm， a dual individual screening method is formed to improve the accuracy of AUV path planning optimal path and increase the convergence speed. The performance of the classical distribution estimation algorithm， PSO algorithm， A* algorithm and the improved algorithm are evaluated in the environment of underwater digital elevation model. The simulation results show that compared with the previous algorithm， the energy consumption calculated by the new algorithm is reduced by 24.9%， which effectively increases the calculation accuracy， avoids falling into local extremum， and improves the efficiency.

Key words：estimation of distribution algorithm， path planning， optimal energy consumption， particle swarm optimization， underwater digital elevation model

自主水下航行器（autonomous underwater vehicle，AUV）作为海洋作业的重要工具，目前已广泛用于执行海底探测、打捞、识别等任务.而作为自主水下航行器的关键技术，路径规划技术一直是机器人控制领域的研究热点.AUV利用已有的海图和采集到的环境信息建立水下环境模型，利用路径规划方法基于环境模型在经济性、安全性、隐蔽性等多约束条件下搜寻最优路径.文献［1］主要通过在目标位置和机器人之间的最短距离建立人工势场法（artificial potential field，APF）中新的排斥势函数，使改进的APF算法能够让机器人在未知环境中开展路径规划.文献［2］主要通过构造新的随机布点法，利用随机函数均匀产生搜索节点构成搜索空间，解决了A*算法在解决AUV路径规划问题上实时避障能力不足的缺陷.文献［3］通过在多层快速步进（multi-layered fast marching，MFM）算法中引入海流流向、障碍物安全距离的因素来节约能源成本，提高算法实用性.文献［4］提出各项异性快速步进算法，通过引入AUV运动学作为约束条件，同时引入自适应网格生成多分辨率方法，提高路径规划速度.但上述算法的缺陷在于人工势场法易陷入局部最优解，A*全局优化能力不足，处理速度慢，快速步进算法（fast marching，FM）迭代时间过长.随着路径规划算法的模拟运行环境越发复杂，传统路径规划算法优化效果差的问题越发明显，一系列智能启发式算法逐渐占据主导地位.文献［5］考虑了AUV的航行特点和海流的运动规律，提出一种基于粒子群优化算法的路径规划算法，缺点是仅于二维环境中验证算法的有效性.文献［6］采用遗传算法进行路径规划，采用二进制编码规则，将AUV实时航向和速度作为影响因子，成功规划出可规避动态障碍物的路径，缺点在于未考虑海流等其他海洋复杂干扰因素的影响.文献［7］提出一种基于自适应等高度直方图的分布估计算法，通过隔代生成随即个体的方法避免算法收敛于局部最优，缺点在于算法运行的三维环境较为简单，同时未考虑其他干扰因素.

作为启发式智能算法的一种，分布估计算法（estimation of distribution algorithm，EDA）被应用于处理AUV路径规划问题，但也存在计算精度低，计算出的路径能耗值难以收敛到最优等问题.因此，文中在EDA的一种算法的迭代过程中融入粒子群优化算法的筛选机制，避免了算法收敛于局部极值，加快了算法的收敛速度，形成一种双重个体筛选法的改进分布估计算法，同时算法计算的适应度函数考虑了AUV的实际能耗，运行的环境采用地理真实环境数据，使仿真结果更贴近实际需求.

1"水下环境模型构建

1.1"水下静态地形模型构建

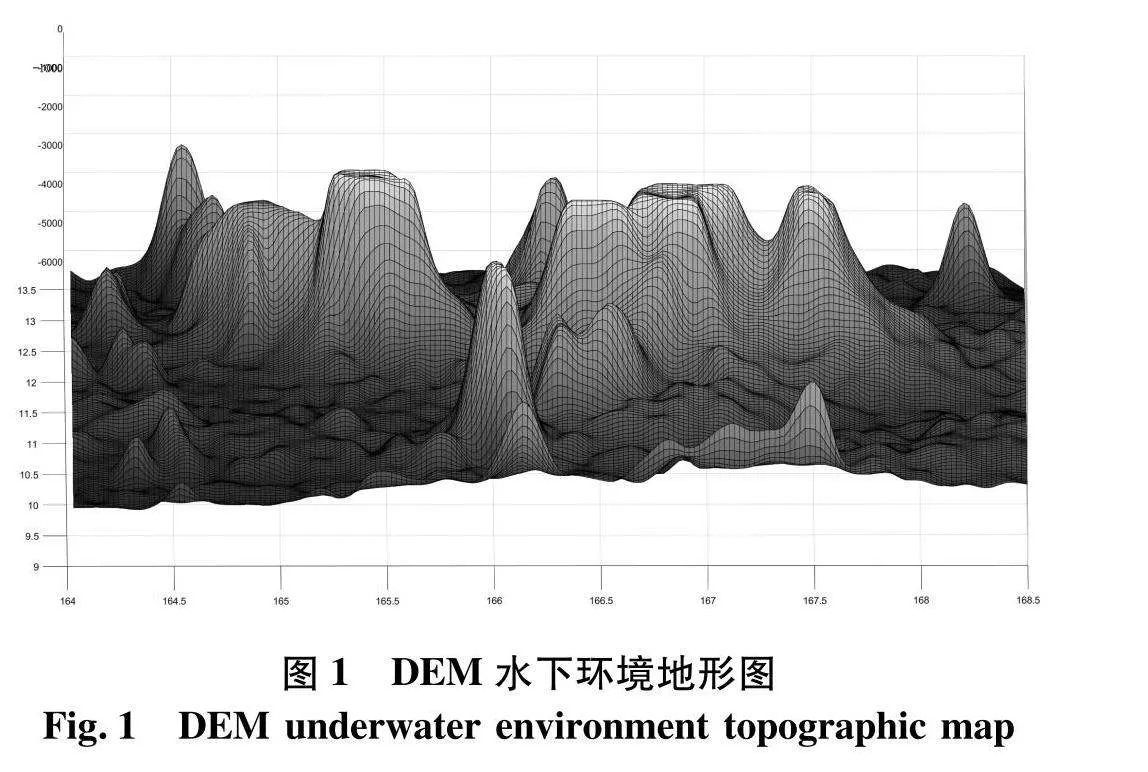
目前各种路径规划算法的研究中环境建模的主要方法有栅格法、可视图法和维诺图法等.近些年地理信息系统（geographic information system， GIS）高速发展，数字地图应用越发广泛.其中栅格型数字地图中的一种，数字高程模型（digital elevation model， DEM）因其数据集离散形式，信息量大，绘制地形的坐标精度高成为主要地图形式.水下数字高程模型存储水下地形分布状态，通过回声探测仪、测深声呐和水面的GPS坐标信息结合而成［8］.文中使用的水下DEM数据来源为国家海洋科学数据中心，数据形式表达为：

Vi=（Xi，Yi，Zi）i=1，2，…，n（1）

式中：（Xi，Yi）为GPS坐标信息；Zi为与坐标对应的深度值.提取目标海域的DEM数据，通过MATLAB绘图生成的三维静态水下地形图，如图1.

1.2"静态海流模型构建

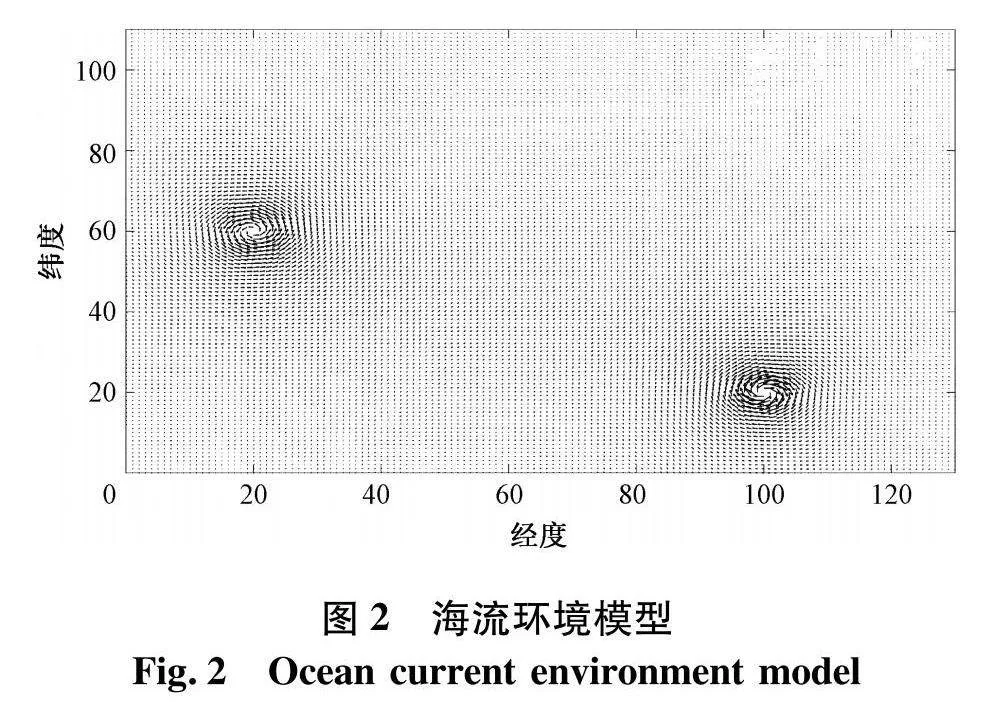
AUV在水下航行过程中会受到各种复杂干扰，其中主要为海流影响.复杂海流的海洋环境可以通过多个粘性Lamb漩涡的叠加来模拟［9］.由于地球的自转，海流在水平面的变化比垂直面更为复杂，因此，模拟的海流环境仅在二维水平面运动.海流模型的数学表示为：

Vx=∑ni=1-τi2π×y-yi（x，y）-（xi，yi）21-e-（x，y）-（xi，yi）2δ2i

Vy=∑ni=1τi2π×x-xi（x，y）-（xi，yi）21-e-（x，y）-（xi，yi）2δ2i（2）

式中：τi为每个漩涡的涡流强度;（xi，yi）为每个漩涡的涡流中心坐标;（x，y）为地图中路径点的坐标;Vx，Vy为海流x和y方向上的分量;δi为每个涡流的半径.其中改变τi值的正负可以改变漩涡的旋转方向，模拟的海流环境模型如图2.

2"AUV能耗模型构建

当考虑海流影响时，AUV的能耗问题变为距离最短能耗非最低问题，这时AUV的能耗由距离因素和海流影响因素叠加而成.这两种因素具体体现在适应度函数中，同时这两种因素也在互相影响.如果适应度函数中对距离的描述与对海流因素的描述不够平衡，此时算法计算的最优路径容易陷入局部最优.因此，在适应度函数中结合AUV的各项实际参数建立真实的距离与海流的关系可以得出更真实的能耗.

AUV在水下航行时主要克服水阻力［10］，AUV受到的水阻力为：

FZ=CρS2VAUV2（3）

式中：C为流体动力系数；S为AUV受力的横截面积；ρ为海水密度；VAUV为AUV的进速.其中VAUV=Vset-Vc，Vset为设定的AUV实际对地的航行速度，Vc为海流速度.

AUV航行时主要能耗为推进器使用的电能，同时由于海流环境产生的不同的水阻力，导致AUV在不同地区克服水阻力时推进器产生的能耗也不同.因此，在适应度函数中，通过推进器能耗可以将移动距离和海流因素有效关联.推进器效率为［11］：

ηthrust=KTKQ×VAUV2πnD（4）

式中：KT为推力系数；KQ为转矩系数；VAUV为AUV进速；n为螺旋桨转速；D为螺旋桨直径.文中使用的AUV推进器经过多次实验测试，采用二次函数拟合后得到KT、KQ、n与VAUV的对应关系为：

KT=-3.470 2×10-4VAUV2-0.088 7VAUV+0.378 9

KQ=-6.185 1×10-4VAUV2-0.002 1VAUV+0.034 8

n=-38.784 4VAUV2+448.633 2VAUV+637.5（5）

AUV航行能耗为：

E=Ptηthrust=FZVAUVtηthrust=FZLηthrust（6）

式中：t为航行时间；L为航行距离；P为推进器功率.则AUV航行的总能耗为：

∑E=∑FZMLM+FZHLH+FZVLVηthrust（7）

式中：FZM、FZH、FZV分别是AUV主推、侧推、垂推克服的阻力，三者的区别在于其受力的横截面积以及螺旋桨进速的不同；LM、LH、LV分别是AUV主推、侧推、垂推行进的距离，3种方向的行进距离计算方法为：

LM=ζ∑ni=1"（Xi+1-Xi）2+（Yi+1-Yi）2

LH=2πLAUV180θ

θ=180π∑ni=1arccos（Xi+2-Xi+1）（Xi+1-Xi）+（Yi+2-Yi+1）（Yi+1-Yi）"（Xi+2-Xi+1）2+（Yi+2-Yi+1）2+"（Xi+1-Xi）2+（Yi+1-Yi）2

LV=∑ni=1Zi+1-Zi（8）

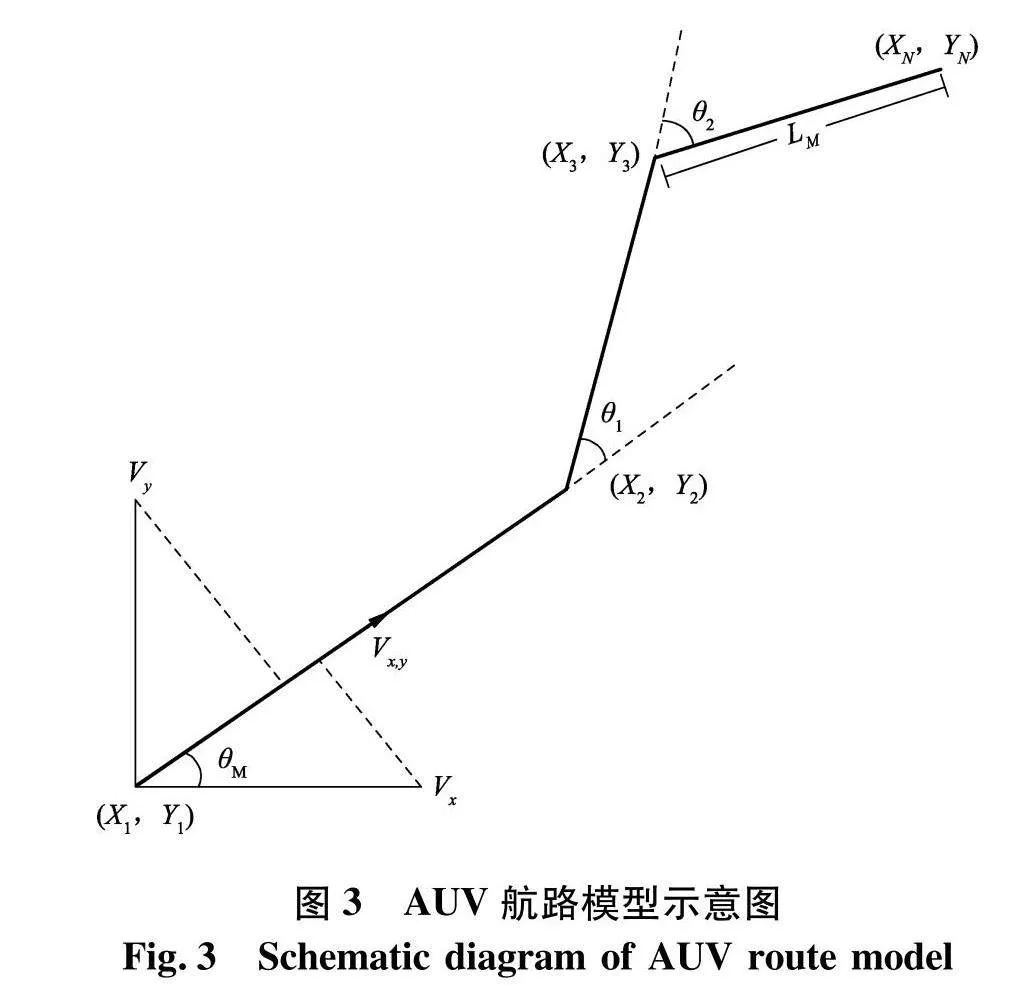
式中：主推LM行进的距离计算方法为DEM数据中坐标点之间的欧式距离.在DEM数据中，垂直距离为测量得出的实际距离，但并没有记录（Xi，Yi）之间的距离，这是由于（Xi，Yi）之间的距离受坐标测量精度的影响.因此式中ζ的作用是用来放大坐标之间的距离，使主推LM行进的距离为真实距离，与侧推、垂推行进距离的度量一致，ζ=101 4.侧推LH行进的距离为AUV在转弯时侧推转过的弧长，半径LAUV为AUV长度的一半，θ为AUV改变方向时侧推转过的角度，假设AUV在航行时不会做横滚运动.

AUV 3个方向的推进器的速度计算方法为：

VAUVM=Vset-（Vxcos θM+Vysin θM）

cos θM=Xi+1-Xi"（Xi+1-Xi）2+（Yi+1-Yi）2

VAUVH=0.007θ

VAUVV=Vset（9）

式中：cos θM为路径中相邻两点之间的夹角，不考虑海流对侧推的影响，侧推速度只与AUV旋转的角度有关.由于海流因素只考虑二维平面，负责AUV垂直运动的垂推不受海流影响，其速度为固定速度.AUV航路模型示意图如图3.

3"改进分布估计算法的路径规划

3.1"基于等宽度直方图的分布估计算法

分布估计算法是一种基于概率模型的进化算法，为了改善遗传算法在求解“积木块”松散分布问题时其交叉操作会破坏“积木块”导致求解精度低的问题，分布估计算法将遗传算法中的交叉操作与变异操作环节替换为构建概率模型，通过概率模型抽样机制产生新种群，依据概率控制种群的分布规律，获得更可靠的信息来引导算法进行探索.不同的概率模型和抽样机制产生了不同种类的分布估计算法.基于固定宽度直方图的分布估计算法（fixed-width histogram，FWH）是一种以固定宽度直方图为概率模型，即将搜索区间划分为宽度相同而高度不同的n个区间，不同高度代表该区间取值概率的大小，依据取值概率在区间内进行采样获取新个体，具有较强全局搜索能力.

FWH算法的具体步骤为：

步骤1"初始化各参数，设置迭代计数器t.

步骤2"依据初始概率随机生成初始总群体P0，初始概率为均匀分布.

步骤3"计算总群体P0中每个个体的适应度值.

步骤4"根据适应度值的大小选择前n个较优势的个体组成优势种群St.

步骤5"根据优势种群St构建等宽度直方图模型.

步骤6"根据直方图模型和采样策略生成新的种群Ot.

步骤7"计算Ot中每个个体的适应度值.

步骤8"用Ot中的个体替换总体P0中适应度值较差的个体形成新的种群Pt.

步骤9"升级迭代次数t→t+1.

步骤10"如果最优秀的个体的适应度值不满足精度或其他终止要求，则转去步骤3；满足则输出最终解.

3.2"算法改进

PjFWHh=Vij|i≤Vij-minjmaxj-minjHlt;h+1N

i∈0，1，…，N-1h（10）

FWH算法的概率模型将每个变量xj（j=1，…，n）的取值区间［minj，maxj］划分为宽度相同而高度不同的H（hj=0，1，…，H-1）个区间，不同高度代表该区间取值概率的大小，V［i］［j］为群体中个体的变量xj的值，N为群体大小［12］.依据取值概率进行采样获取新个体.相比于高斯网络的概率密度模型，直方图法估计概率密度更加直接.FWH在迭代时，会根据适应度值的大小选取前n个较为优势的个体为参考进行下一次迭代，其余较为劣势的个体会根据优势个体的分布重新采样参与下一次迭代，其中n值设置的大小与寻优速度关系密切.n值设置过大，被认为是较优势的个体占总群中的个数较多，虽然每次迭代时种群的多样性增加，但寻优速度缓慢，算法收敛速度慢.n值设置过小，迭代时种群的多样性减少，算法容易陷入局部最优.因此，在不增加n值的情况下增加迭代过程中的种群筛选机制可以保证种群多样性和寻优速度，同时不易陷入局部极值.

同为启发式算法，粒子群优化算法（particle swarm optimization，PSO）的种群筛选机制与分布估计算法完全不同，其种群的更新不是通过概率模型，而是根据每一代的个体最优路径和全局最优路径改变更新速度进行路径更新.PSO算法更新速度和位置为：

Vi=wVi+c1r1pbesti-xi+c2r2gbesti-xi

xi=xi+Vi（11）

式中：Vi为粒子的速度；r1、r2为［0，1］之间的随机数；c1、c2为学习因子；xi为粒子的当前位置；pbesti为个体最优路径；gbesti为全局最优路径.PSO在解决路径规划问题时每个粒子为每一条路径.

PSO算法与FWH算法在进行种群更新时的区别在于PSO算法每次更新时每一条路径需要根据这条路径的历史最优路径即个体最优路径更新速度，进而产生下一次迭代的路径，而FWH算法每次更新最优路径时虽然会记录前n个较优势的个体，但其他个体的更新并不需要与之前的个体进行对应比较，而是通过适应度值优胜劣汰，不需要记录每个个体在种群当中的位置.因此，在原有FWH更新种群的方法中融合式（12）的种群筛选机制，形成PFWH算法.

Vi=c2r2gbesti-xixi=xi+Vi

gbesti=gbesti（1+randn）（12）

式中：randn为符合高斯分布的随机数.

由于FWH算法不需要记录每条路径在群体中的位置，因此，与PSO更新速度方法不同，PFWH在更新部分劣势个体的速度时不需要参考初始速度和个体最优路径，式（12）中c2r2的作用是限制个体更新时增加的速度，防止产生的个体超出地图边界.

FWH算法的缺陷在于其计算出的最优路径最终仅能收缩至某一特定区间内，由于其取值区间无法收缩，导致最终计算的结果会在这一特定区间内随机取值.而PSO算法的个体更新具有方向性，同时由于速度可变最终会收敛至某一特定路径而不是一个固定范围，但由于其根据每代的最优个体更新种群，如果算法收敛时最优个体并非全局最优，则算法依然会收敛于局部最优.而种群通过FWH和PSO算法计算的路径进行比较，两种更新机制更易产生全局最优路径.在算法未收敛的迭代过程中，全局最优路径gbesti并非算法最终的最优路径，为了防止融合的算法在更新个体时陷入局部最优，对公式中的最优个体gbesti进行高斯变异，使其有概率跳出局部最优，改变搜索方向.

改进后的算法PFWH算法步骤：

步骤1"初始化各参数，设置迭代计数器t.

步骤2"依据初始概率随机生成初始总群体P0，初始概率为均匀分布.

步骤3"计算总群体P0中每个个体的适应度值.

步骤4"根据适应度值的大小选择后m个较为劣势的个体，根据式（11）产生较为优势的个体.

步骤5"根据适应度值的大小选择前n个较优势的个体构建等宽度直方图概率模型.

步骤6"根据直方图模型和采样策略生成新的种群并与步骤4中产生的个体进行比较，更新P0.

步骤7"升级迭代次数t→t+1.

步骤8"如果最优秀的个体的适应度值不满足精度或其他终止要求，则转去步骤3；满足则输出最终解.

4"仿真实验

在众多基于栅格环境的路径规划算法研究当中，算法的适应度函数中需要增加判断路径安全性，即需要判断路径点是否会碰撞障碍物.其缺陷在于如果一条路径的其中一个航路点不安全，其适应度值会被设置的放大系数增大，整条路径会在迭代中淘汰，即使这条路径的其他路径点组成了最优路径.这样算法的收敛速度会减慢，甚至不收敛.因此，基于DEM数据格式，生成的路径格式如式（13）.在路径生成个体的Z轴值时，提供每个路径点的参考Z轴值，算法在参考Z轴值附近划分区间进行采样.相比于在适应度函数中设置安全判定函数，设置参考Z轴值的优势在于群体中每条路径均为可行路径，加快收敛速度.参考Z轴值设定方法为式（14）.

Path=X0，X1，…，Xn

Y0，Y1，…，YnZ0，Z1，…，Zn（13）

Zi=ZE-ZS"XE-Xi2+YE-Yi2XE-XS2+YE-YS2（14）

式中：（XS，YS，ZS）为路径中起点；（XE，YE，ZE）为终点；（Xi，Yi，Zi）为路径中间点.算法寻优的过程即为寻找最优Xi，Yi的过程.

文中基于六自由度AUV，因此在路径规划中未考虑AUV转向角以及路径平滑度的问题.最终规划出能耗、路径长度达到最优并能成功避障的路径.仿真环境以坐标为（E164.030 831 798 2， N13.195 392 451 1）附近的海底DEM数据集为基础，构建了水下仿真环境，算法依据起始点和终止点的X轴值的个数划分为多个切片，每个切片划分Y轴值区间个数设为10，每个区间Z轴值采样个数为50，算法的终止条件为迭代次数200次.为了减少计算量，简化算法程序，将原始DEM模型中的坐标数据进行加权处理为整数，其中起点与终点的GPS坐标及深度经过加权处理后的坐标如表1.AUV以及各公式中的常量设置如表2.

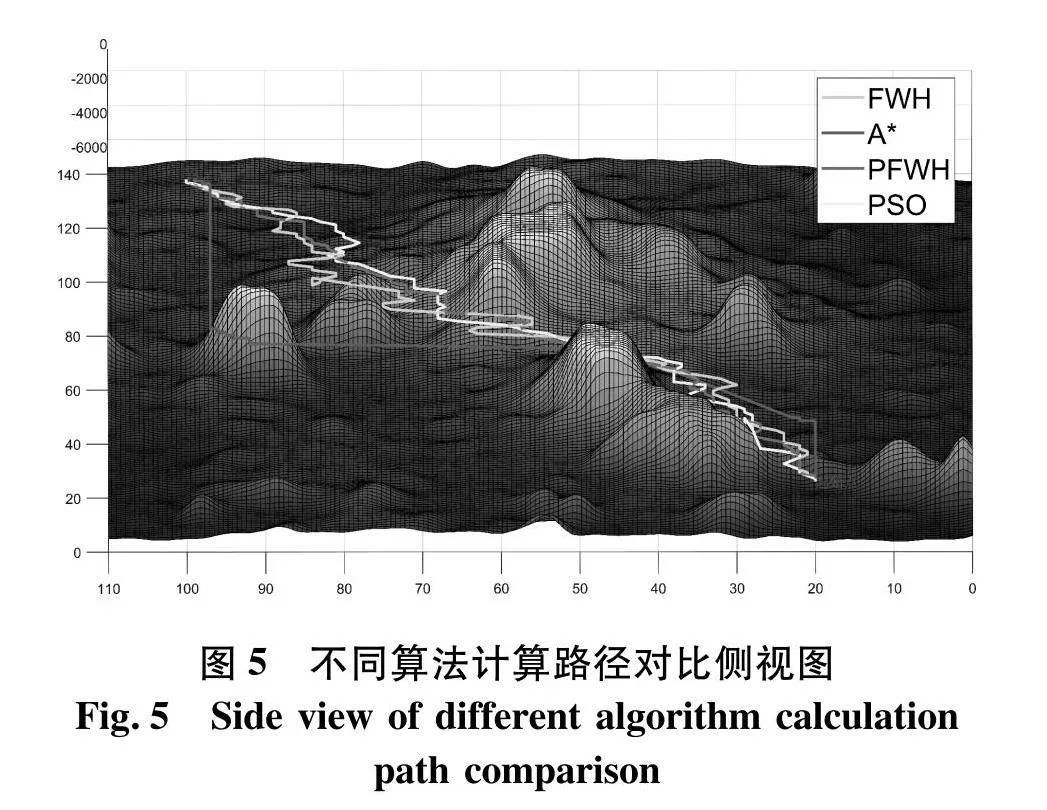
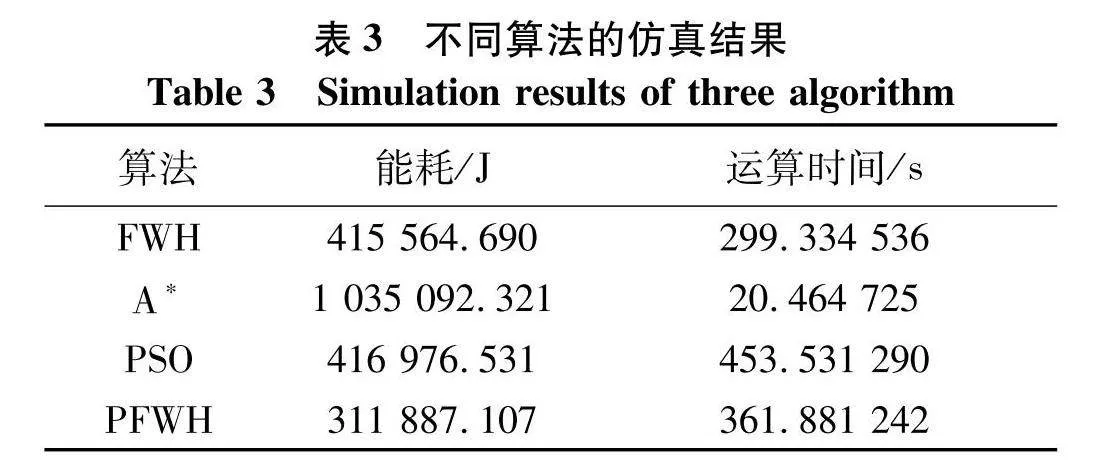
如图4，5，文中的算法与经典路径规划算法中的A*算法以及其他智能启发式算法相比，路径更平滑.虽然A*的计算时间明显更少，由于搜索环境的复杂度高，其更易陷入局部极值.

图4、5中可以看出，相比于FWH算法，PFWH算法产生的路径更加平滑.但由于增加了计算量导致PFWH相比于FWH计算速度增加了20%左右.

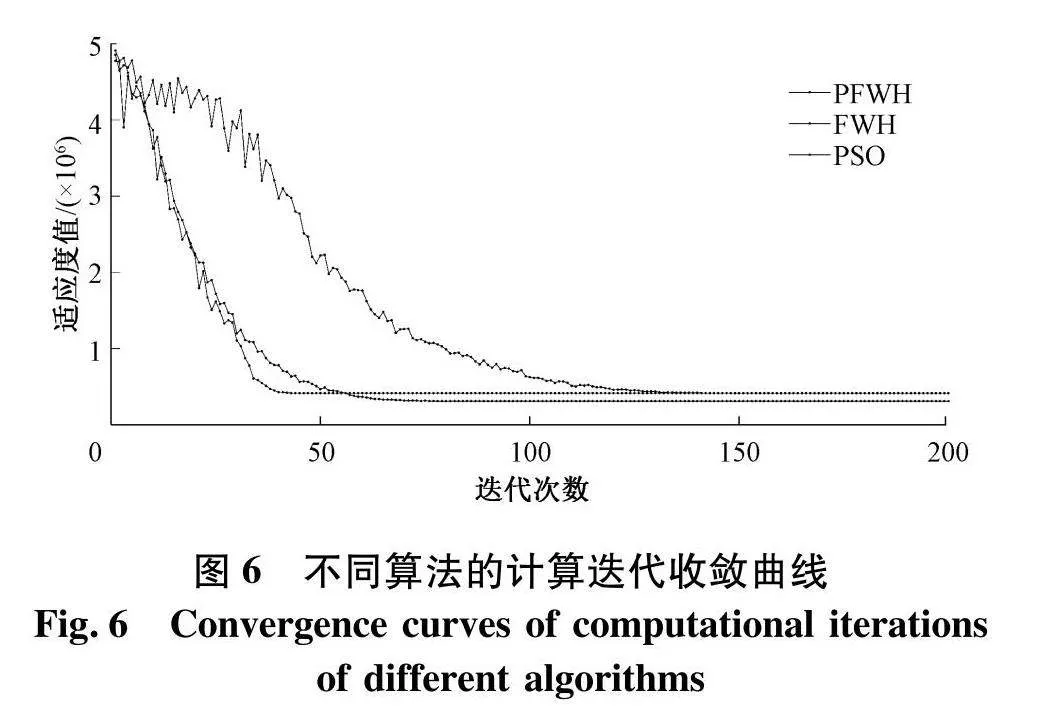
如图6，FWH算法的收敛速度明显慢于PSO算法和PFWH算法，但得出的最优路径的能耗值FWH和PSO差距较小.由于PFWH在产生优势个体时采用了FWH的概率模型和PSO的部分优势个体生成机制相融合的方法，迭代过程中每代的劣势个体经过式（12）的筛选得出更为优势的个体，使群体的优势个体比例增大，优势个体的选择更具多样性，其收敛速度更接近于PSO，但最优路径的能耗值相比其他两种算法降低了24.9%和25.2%.PFWH通过融合的双优势个体产生机制可以在迭代中优势个体多样性多于FWH，同时，PFWH的种群中包含了比PSO更多的可能路径，在迭代次数40～50次PSO由于种群多样性较少则开始收敛于局部最优，而PFWH并未立即收敛，这是因为算法在FWH产生的优势个体的基础上通过PSO算法的个体更新机制进一步优化产生更优势的个体.

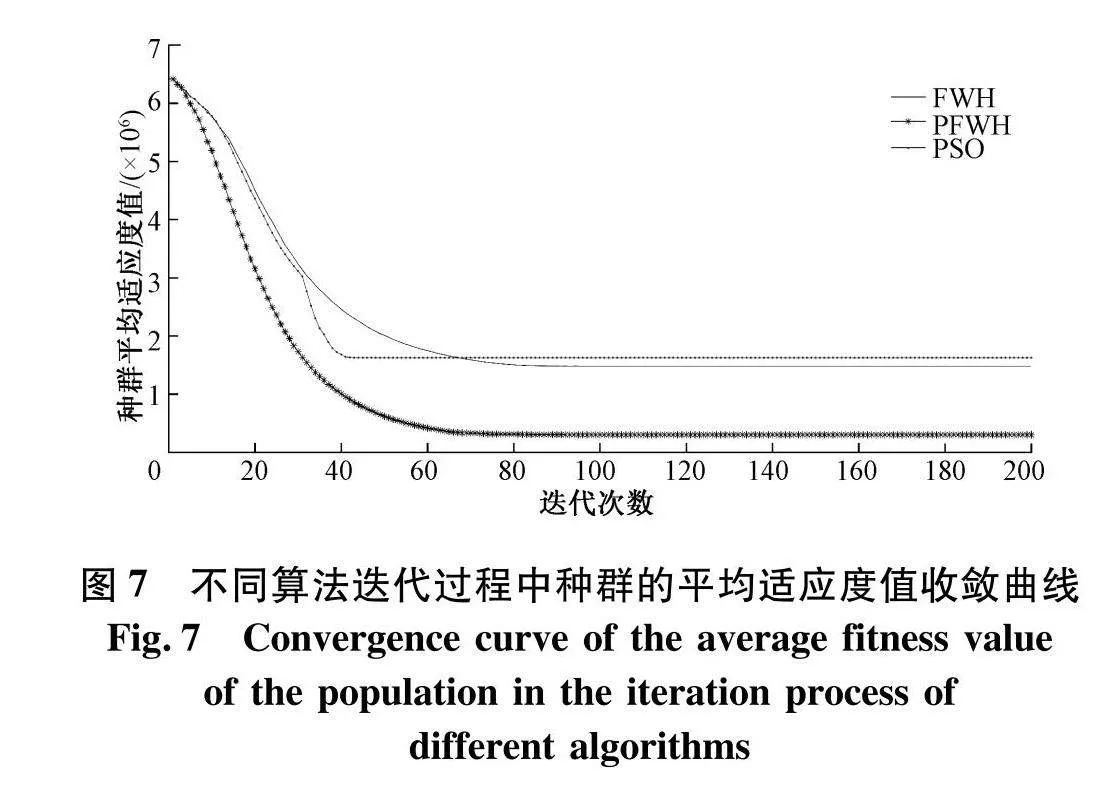
图7反映了不同算法迭代过程中整个种群的平均适应度值变化，由于PFWH采用两种方法同时筛选优势个体与劣势个体，其迭代过程中种群的平均适应度值更低，表明不论种群中的优势个体还是劣势个体，PFWH算法中的每个个体均比改进前的算法更优.同时由于式（12）中个体进行高斯变异的影响，算法更容易避免收敛于局部极值，使得改进后的算法趋于收敛后其群体中的路径相比于改进前有较大优化.

5"结论

基于固定宽度直方图分布估计算法与粒子群优化算法，提出一种改进分布估计算法，实现AUV能耗最优路径规划.通过将粒子群优化算法的部分优势个体筛选机制以及收敛前的最优个体的高斯扰动融合到FWH算法中，形成双重优势个体生成机制，增加种群多样性，使算法避免过早收敛，提高AUV路径规划的精度.仿真结果表明，文中算法在计算AUV在三维空间中的路径规划时，改进后的算法相比FWH算法与PSO算法路径能耗更小，精度更高，计算时间略有增加.

参考文献（References）

［1］"NGANGBAM H S， SALAM S D， KHELCHANDRA T.Modified artificial potential field approaches for mobile robot navigation in unknown environments［C］// International Conference on Soft Computing for Problem Solving. Berlin：Springer，2019：319-328.

［2］ 程志，张志安，李金芝，等.改进人工势场法的移动机器人路径规划［J］.计算机工程与应用，2019，55（23）：29-34.

［3］ SONG R， LIU Y C， RICHARD B. A multi-layered fast marching method for unmanned surface vehicle path planning in a time- variant maritime environment［J］. Ocean Engineering， 2017， 129：301-317.

［4］ ZHANG H H， LIMING G， TAO C， et al. Global path planning methods of UUV in coastal environment［C］//Proceedings of the 2016 IEEE International Conference on Mechatronics and Automation. Piscataway： IEEE， 2016：1018-1023.

［5］ 冯炜，张静远，王众，等.海洋环境下基于量子行为粒子群优化的时间最短路径规划方法［J］.海军工程大学学报，2017，29（6）：72-77.

［6］ 严浙平，黄宇峰，李锋.遗传算法在AUV局部路径规划中的应用研究［J］.应用科技，2009，36（2）：46-51.

［7］ LIU Rundong， ZHAN Zhihui， CHEN Weineng .Estimation of distribution algorithm for autonomous underwater vehicles path planning［C］//International Symposium on Neural Networks. Cham：Springer， "2018：647-655.

［8］ 汤国安，李发源，刘学军数字高程模型教程［M］.3版.北京：科学出版社，2016：45-53.

［9］ GARAU B， ALVAREZ A， OLIVER G. AUV navigation through turbulent ocean environments supported byonboard H-ADCP［C］//Proceedings 2006 IEEE International Conference on Robotics and Automation.Orlando： IEEE， 2006： 3556–3561.

［10］ 徐炜翔，朱志宇.基于飞蛾火焰算法的AUV三维全局路径规划［J］.上海理工大学学报，2021，43（2）：148-155.

［11］ 秦玉峰，齐占峰，彭家忠，等.小型长航程AUV续航力分析［J］.水下无人系统学报，2019，27（3）：346-354.

［12］ TSUTSUI S， PELIKAN M ， GOLDBERG D E .Evolutionary algorithm using marginal histogram models in continuous domain［J］.IIIi GAL Report， 2001，2001019：105.

（责任编辑：曹莉）