响应电网频率的电车充电站分层实时调度

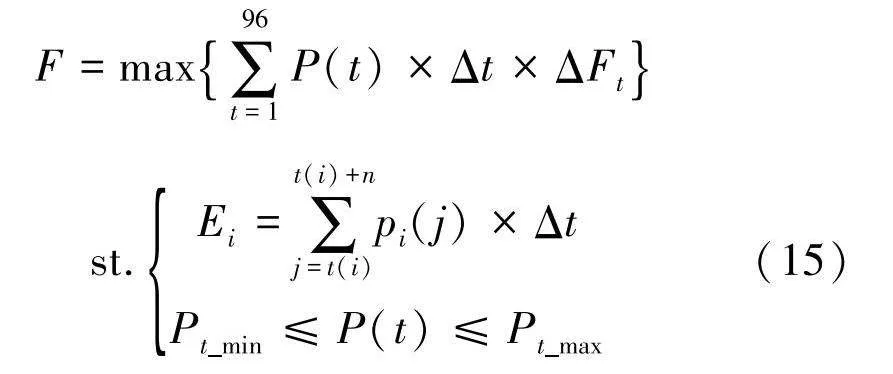
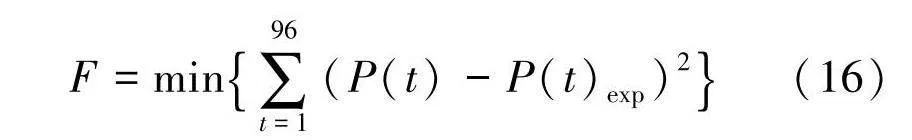
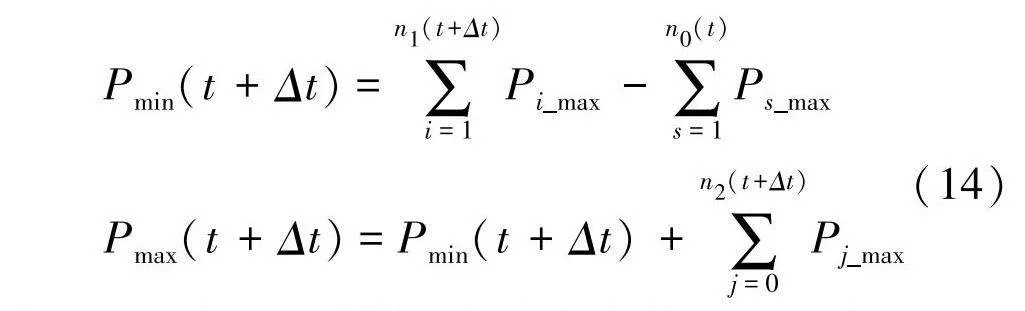
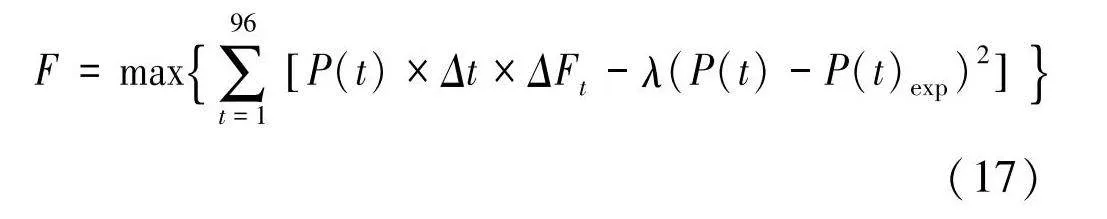
摘"要： 针对充电站内大量电动汽车负荷的实时调度问题，提出了一种分层式的实时调度策略，分别以充电站效益、指导功率追踪以及综合考虑效益和追踪三种方案作为上层优化目标，采用粒子群算法进行寻优得到充电站负荷的优化值.基于上层优化的结果，提出基于用户充电需求紧迫程度并计及电网实时频率的充电功率分配方法为电动汽车制定充电方案.最后通过算例验证了该分层实时调度策略的有效性，能够在满足电动汽车充电需求的基础上，满足充电站与电网的经济运行.

关键词： 电动汽车；分层控制；实时调度；频率响应

中图分类号：TM761"""文献标志码：A"""""文章编号：1673-4807（2024）04-092-08

Layered real-time scheduling strategy considering frequency responsefor electric vehicle stations

XIAO Yi1， LOU Nan1， WANG Ke1， YANG Lin1， ZHANG Yong1，FANG Biwu1， CHEN Qian2， ZHANG Xiao3

（1. Southern Power Grid Co. Ltd.， Power Dispatching Control Center， Guangzhou 510062， China）

（2. College of Energy and Electrical Engineering， Hohai University， Nanjing 211100， China）

（3. Nanjing Nari Relays Electric Co. Ltd.， Nanjing 211100， China）

Abstract：In this paper， a hierarchical strategy is proposed for real-time scheduling of a large number of electric vehicle loads in charging stations. Taking the three schemes， based on benefit of charging station， tracking reference power， and integration of benefit and tracking respectively， as the upper optimization objective， the optimal load value of charging station is obtained by using particle swarm optimization algorithm. According to the results of upper optimization， a charging power allocation method based on urgency of users′ charging demand considering frequency response is proposed to formulate a charging scheme for electric vehicles. Finally， the effectiveness of the layered real-time scheduling strategy is verified by an example， which can meet both the charging demand of electric vehicles and the economic operation of charging stations and power grids.

Key words：electric vehicle， hierarchical control， real-time scheduling， frequency response

电动汽车具有清洁、高效的优点［1］，随着社会的发展，电动汽车将会成为未来出行的主流交通工具［2］.目前电动汽车的发展主要受限于基础充电设施的建设，一方面小规模离散的充电桩虽然对电网影响较小，但是难以满足大量的充电需求［3］.另一方面，大规模充电站的建立使供电台区内大量的电动汽车负荷接入电网，对电网造成不利影响［4］.因此针对充电站的站内充电负荷调度控制开展深入研究具有重要的意义［5］.

充电站调度控制技术［6］的应用是减小规模化电动汽车接入电网造成不利影响的有效措施.开展调度控制技术的研究是为了能够实现电动汽车的有序充电［7］.有序充电能减小充电负荷对电网带来的压力，甚至参与电网的频率响应，其研究主要有两个角度：第一类是从电网的需求考虑，研究在满足用户充电需求的前提下，根据电网与用户提供的信息调节电动汽车的充电功率与充电时段，实现降低负荷波动与峰谷差的目的［8］；第二类是从用户的需求出发，通过需求侧响应引导用户参与有序充电过程.通常是制定分时电价策略，通过电价激励或补贴的方式，降低用户充电费用，引导用户参与有序充电，达到降低负荷峰谷差的目的［9-10］.

由于单一目标优化难以满足充电站与电网的运行要求，目前针对电动汽车有序充电的控制越来趋向于多目标化.文献［11］基于博弈理论，以负荷方差作为调峰水平的指标，综合考虑电动汽车充电等待的时间，制定了降低电网负荷方差与提高充电站利润双重目标的优化策略；文献［12］将用户成本作为第一层目标，电网负荷波动作为第二层优化目标，设计了双目标分层优化的模型，为有序充电调度提供依据.

国内外针对电动汽车有序充电的策略与应用都开展了深入的研究.但考虑电网频率补偿的充电站负荷实时调度的应用还存在一定的困难.文中在某些汇集点测量电网频率，然后按照一次调频的响应策略将响应功率分配到指定设备，具有测量精度高、响应协同性好、总体成本较低的优点.所提出的站内分层实时调度策略，有利于实现实时优化的同时减少计算时间，提供工程可行性.

1"电动汽车充电负荷建模

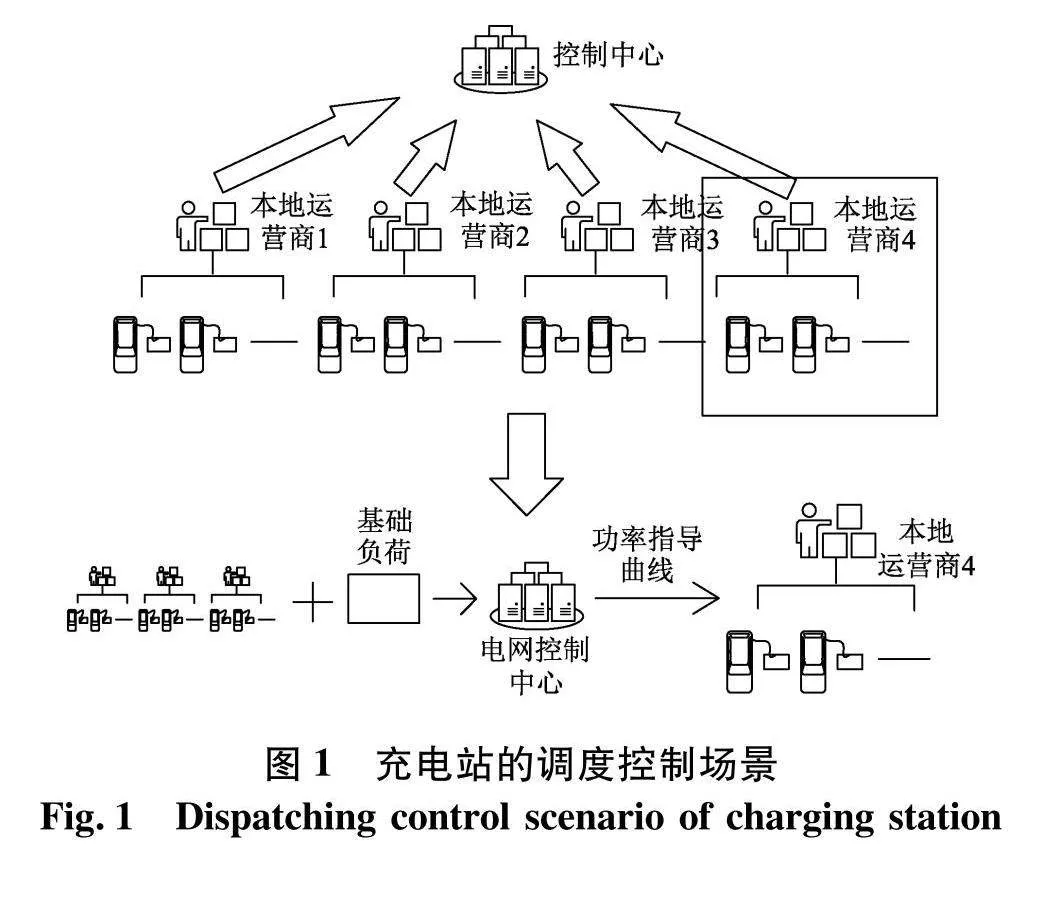
1.1"充电站的调度控制场景

充电站如图1，电网控制中心根据区域内其它负荷以及本地运营商4的历史数据，通过设定的优化目标进行离线计算，为运营商4下发了日前功率指导曲线.

而本地运营商4根据电网控制中心下发的功率指导曲线通过设定优化目标优化充电站的负荷.并根据优化结果，为站内电动汽车合理的分配充电功率.

1.2"电动汽车充电场景构建

研究电动汽车的充电行为能够建立有效的充电模型，充电行为的主要因素包括：初始荷电状态、电池的容量、完成充电后的电量、充电起始时间、停车时间、充电方式、充电频率和选择的充电站位置.

根据2017年美国交通部发布的全国家庭旅行调查报告［13］，拟合了23 474组私家车每日最后一次回家的时间分布函数，作为处于居民区电动汽车充电开始时间的分布函数，得到正态分布为：

f（t）=12π×σe－（t－μ）22σ2"（μ－12）lt;t≤24

12π×σe－（t+24－μ）22σ2"0lt;t≤（μ－12）（1）

式中：t为时间；期望值μ=17.6，标准差σ=3.6.

汽车每日最早离开时间的分布，可以拟合得到充电结束时间的分布函数：

f（t）=12π×σe－（t－μ）22σ2"0lt;t≤（μ+12）

12π×σe－（t－24－μ）22σ2"（μ+12）lt;t≤24（2）

式中：期望值μ=8.3，标准差σ=3.2.

车辆的日均行驶里程整体呈现泊松分布的趋势，而不同电动汽车单位千米的耗电量基本相当，因此可以认为电动汽车的日均电荷量需求也有相似的趋势.因此初始荷电状态分布将以泊松分布表示，其期望值设定在30%～40%，符合大多数车主的正常使用习惯.

通过以上分析得到了电动汽车各参数的分布函数.通常建立充电汽车模型可以采用蒙特卡罗模拟.系统模拟过程中由于不需要海量的数据，因此采用拉丁超立方抽样（Latin hypercube sampling， LHS）生成电动汽车的充电场景.拉丁超立方抽样属于分层抽样，能够在采样样本数较少的情况下反映被采样值的理论分布.

若有变量X的累积分布函数为式（2），则其反函数为：

Y=F（X）（3）

Y=F-1（X）（4）

假设生成的电动汽车数量用N来表示.LHS首先将特征参数累积分布函数的纵轴等分为N个区间，然后在每个区间中进行抽样，抽样得到的点对应的反函数就是该特征参数的一个样本，可以表示为：

xn=F－1（yn）（5）

若电动汽车参数中含有K个随机变量，对每个随机变量的累计分布都进行LHS采样，把采样结果合在一个行向量中得到一个K×N阶的矩阵X为：

X=x11x21…xN1

x12x22…xN2

x1Kx2K…xNK（6）

每一列就代表了一台电动汽车的参数信息.由于每个参数之间是独立的，为了降低各参数之间的相关性，需要对采样值进行重新组合.采用柯列斯基分解法，其步骤如下：

① 生成一个K×N阶的矩阵L，其第k行的元素由整数1－N随机排列而成，每个元素代表了X矩阵行向量中元素的位置；

② 计算L矩阵各行之间的相关系数矩阵ρ，ρ是一个K×K阶的矩阵，可以表示为：

ρ={ρij，i=1，2，…，K;j=1，2，…，K}（7）

式中：ρij表示第i行和第j行之间的相关系数，其数学表达式为：

ρij=∑Kk=1［（Lik-Li）（Ljk-Lj）］

∑Kk=1（Lik-Li）2∑Kk=1（Ljk-Lj）2（8）

③ 可见ρ是一个正定对称矩阵.通过对相关系数矩阵使用柯列斯基分解，可以得到非奇异的下三角矩阵D满足：

ρ=DDT（9）

④ 根据式（8）计算得到K×N阶矩阵G：

G=D-1L（10）

⑤ 根据矩阵G中行向量元素的大小，将L中对应位置的元素进行排列；

⑥ 将矩阵X中行向量的元素按照重新排列后的矩阵L中对应的行向量元素所指示的位置进行重新排列.

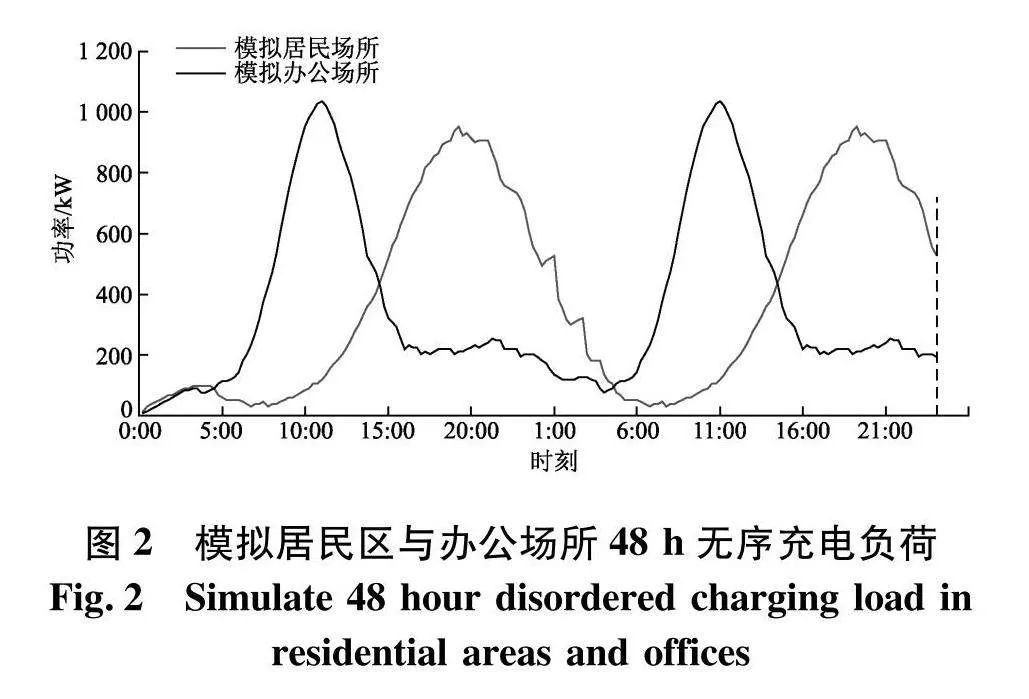
通过以上步骤生成的充电场景，可以有效的减少电动汽车参数之间的相关性，保证入站充电汽车状态的随机性.得到两个模拟充电场景48 h负荷，如图2.

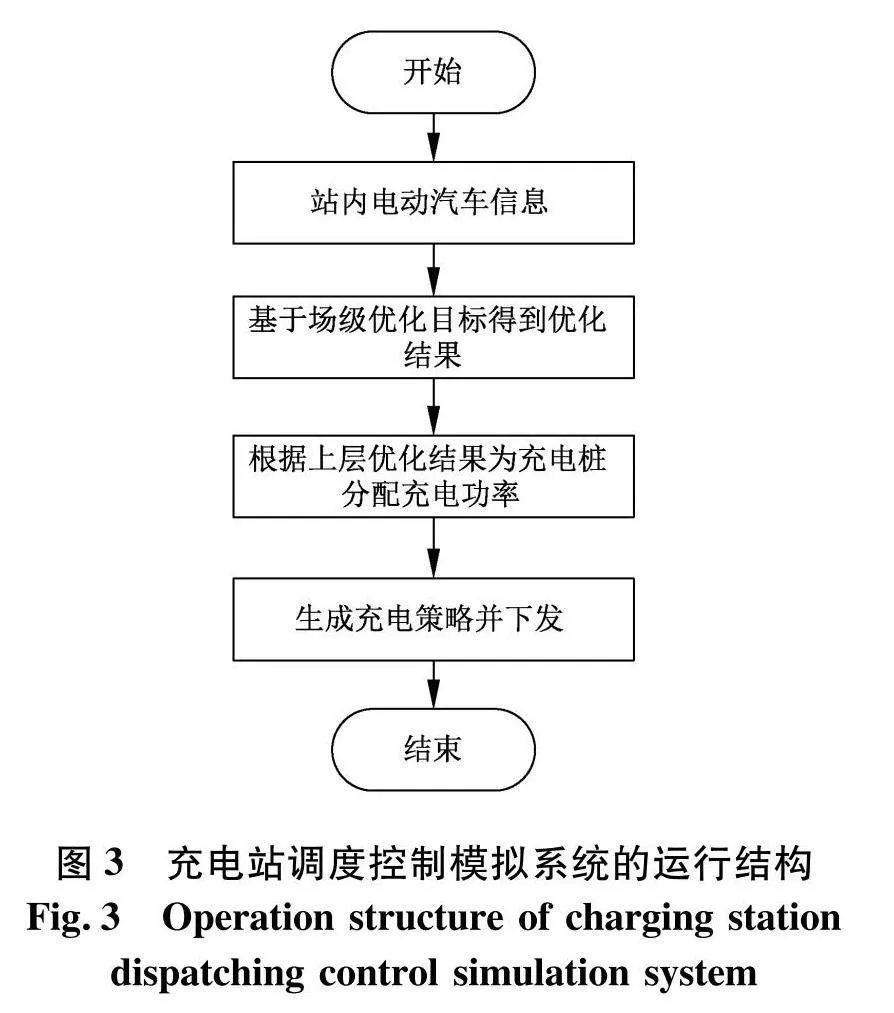
2"充电站实时优化上层控制策略

充电站实时分层控制的过程如图3.通过上层优化能够实现对充电站负荷的优化.

2.1"充电站负荷的调度空间分析

充电站负荷的可调度空间等于当前时刻站内充电可调度的电动汽车集合.电动汽车充电的可调度性，可以理解为车辆是否有富余的停车时间供充电站调度.当然车辆的可调度性不仅与充电时间有关，还与其最大充电功率及电量需求有关.因此定义了充电裕度指标k为：

k=Pmax×Tleave×ηE（t）（11）

式中：Tleave为该车辆的预计剩余停车时长；Pmax为能获得的最大充电功率；η为充电效率；E（t）为t时刻该电动汽车的电量需求：

E（t）=（SOC期望－SOCt）×Capacity（12）

式中：SOC为电池荷电系数.由上述定义可以看出，当电动汽车的klt;1时，在剩余停车时间内即使以最大充电功率Pmax为其充电都不能满足其电量需求Et；k=1时，表示剩余时间内以Pmax充电才能满足其电量需求；kgt;1表示该电动汽车具有参与调度的能力，为充电站提供了可调度空间.则t时刻充电站负荷的最大值、最小值分别为：

Pmin（t）=∑n1（t）i=1Pi_max

Pmax（t）=∑n1（t）i=1Pi_max+∑n2（t）j=1Pj_max（13）

式中：功率下限Pmin（t）为在充汽车中k≤1的最大充电功率之和；功率上限Pmax（t）为所有在充电动汽车的最大充电功率之和；n1（t）为t时刻k≤1的车辆数；n2（t）为t时刻kgt;1的车辆数；Pi_max、Pj_max分别为电动汽车i、j能够获得的最大充电功率.

在优化过程中，如果仅考虑当前时刻充电站内的电动汽车负荷约束，难以达到整体最优的效果，还需要对未来时间段充电站的负荷可调度空间进行分析.在不考虑电网对充电站约束的情况下，下一控制时段充电站的可调度空间就是去除当前时段已完成充电的汽车加上预测新进入充电站汽车的调度范围，可以表示为：

Pmin（t+Δt）=∑n1（t+Δt）i=1Pi_max－∑n0（t）s=1Ps_max

Pmax（t+Δt）=Pmin（t+Δt）+∑n2（t+Δt）j=0Pj_max（14）

式中：n0（t）为t时段内完成充电的电动汽车；n1（t+Δt）、n2（t+Δt）分别为t+Δt时刻充电站内k≤1、kgt;1的电动汽车.

但是通过这种方法预测得到的充电站各控制时段的负荷调度范围是相关联的，如果滑动的窗格较长，会导致优化过程中产生指数级的计算量，难以工程实用化.一般可以用电网控制中心根据台区历史基础负荷与充电站历史信息计算得到的指导功率范围作为可调度空间的约束范围.为了防止调度结果不能满足站内电动汽车的充电需求，需要对当前时刻充电站的功率限制进行研究.

图4为当前时刻充电站可调度空间与电网约束之间可能存在的关系.Pg_max、Pg_min分别为电网提供的指导功率范围，P1（t）～P6（t）为t时刻充电站可调度空间可能出现的情况.为了能够防止优化调度结果越限，同时使调度结果尽量在电网约束范围内，在滚动的过程中，应根据表1调整当前时刻的功率约束范围.

2.2"上层优化调度策略

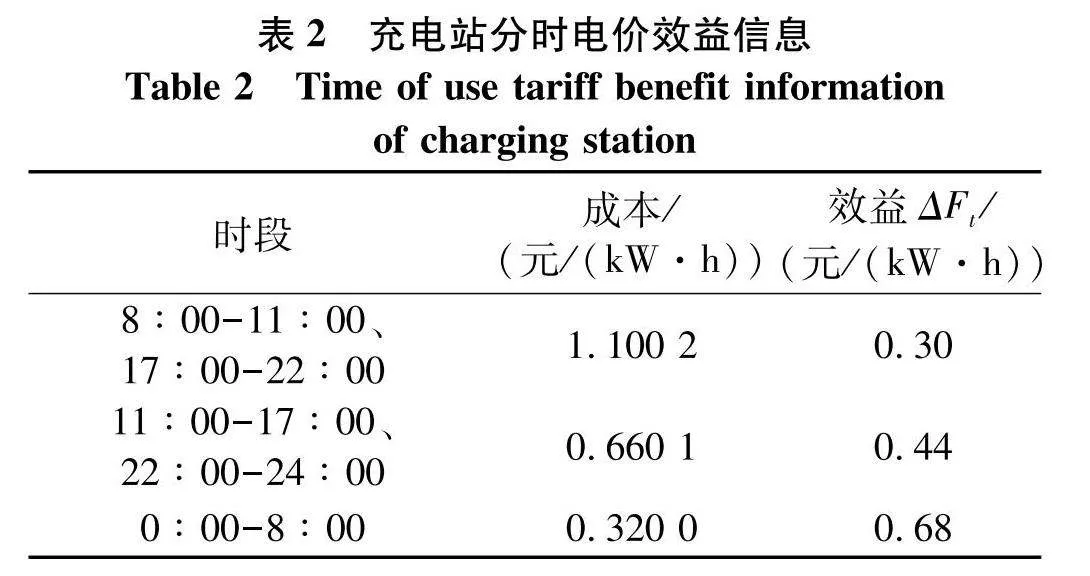
分时电价机制的建立是为了引导负荷需求的转移，如果充电站在满足用户充电需求的基础上，合理的利用分时电价对充电负荷进行调度，就可以有效的降低充电成本，提高充电站效益.文中在传统分时电价的基础上，制定了充电站运营效益优化的策略.分时电价采用某省发布的电价信息，其中含有峰期、谷期、平期3个阶段，假定每个阶段对应的单位电价效益如表2.

由于系统的控制时段Δt=15 min，则目标函数与约束条件为：

F=max∑96t=1P（t）×Δt×ΔFt

st.Ei=∑t（i）+nj=t（i）pi（j）×Δt

Pt_min≤P（t）≤Pt_max（15）

式中：ΔFt、P（t）为t时刻的单位售电效益和充电站功率；Ei为电动汽车i的电量需求；t（i）、t（i）+n分别为汽车i的充电起止时间；pi为电动汽车的充电功率；Pt_max、Pt_min分别为t时刻充电站的可调度功率的上、下限值.

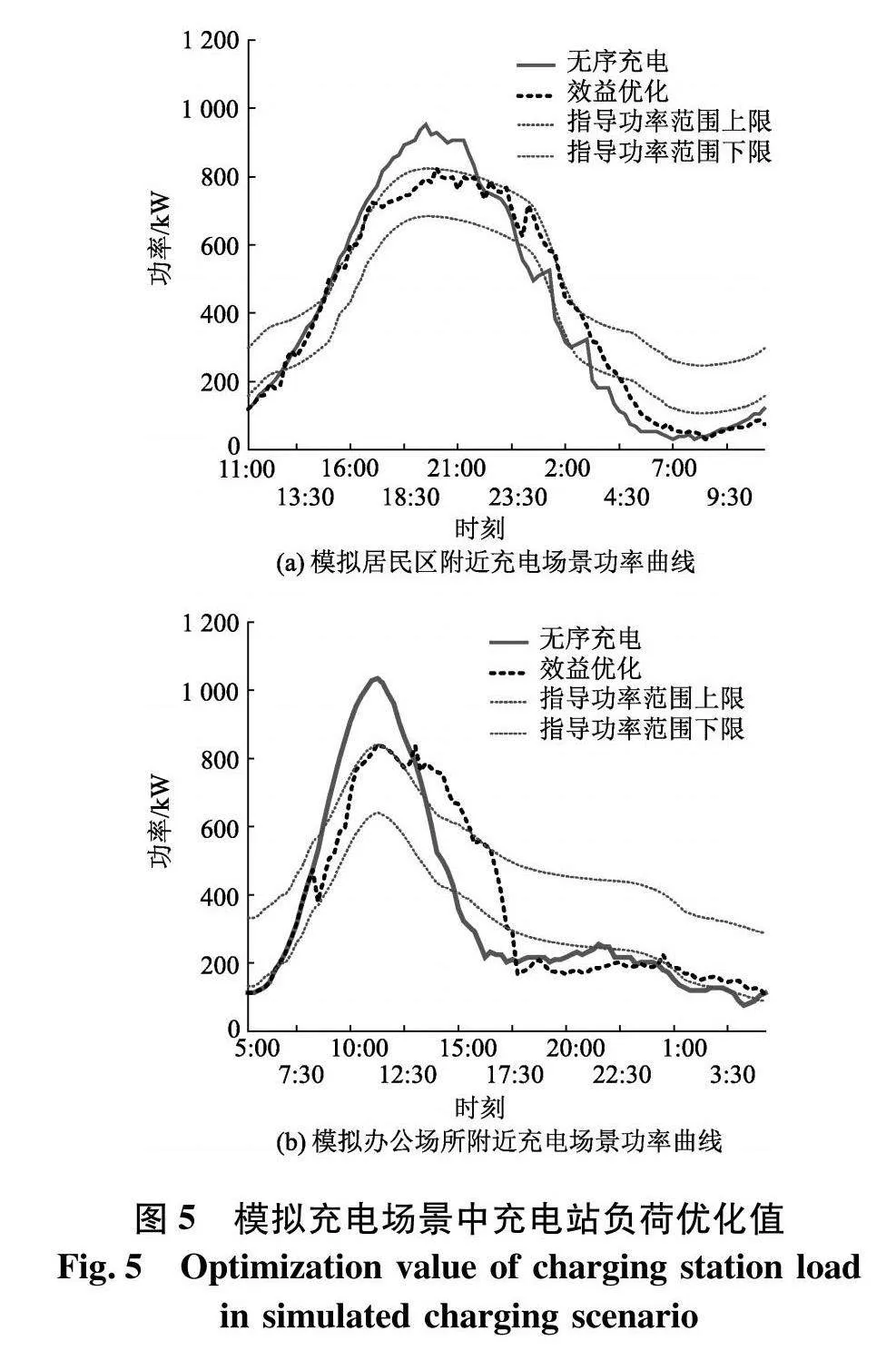
通过粒子群算法进行寻优得到两个模拟充电场景中充电站负荷优化值曲线如图5.

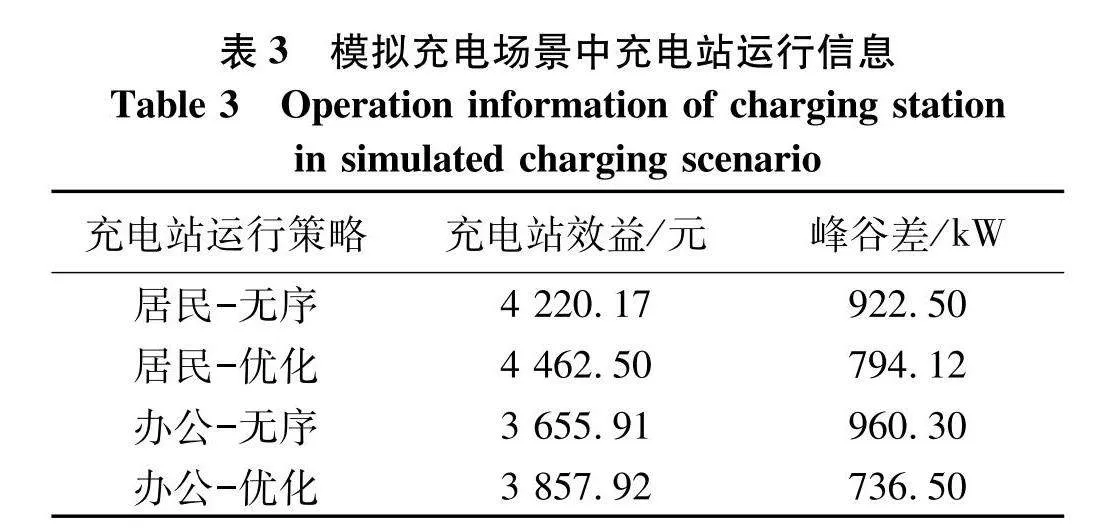
充电站运行信息如表3.

相比于无序充电，该方案能够实现充电站效益的优化.改变目标，以电网对充电站负荷的功率约束中间值作为指导功率进行追踪优化.其目标函数为：

F=min∑96t=1（P（t）－P（t）exp）2（16）

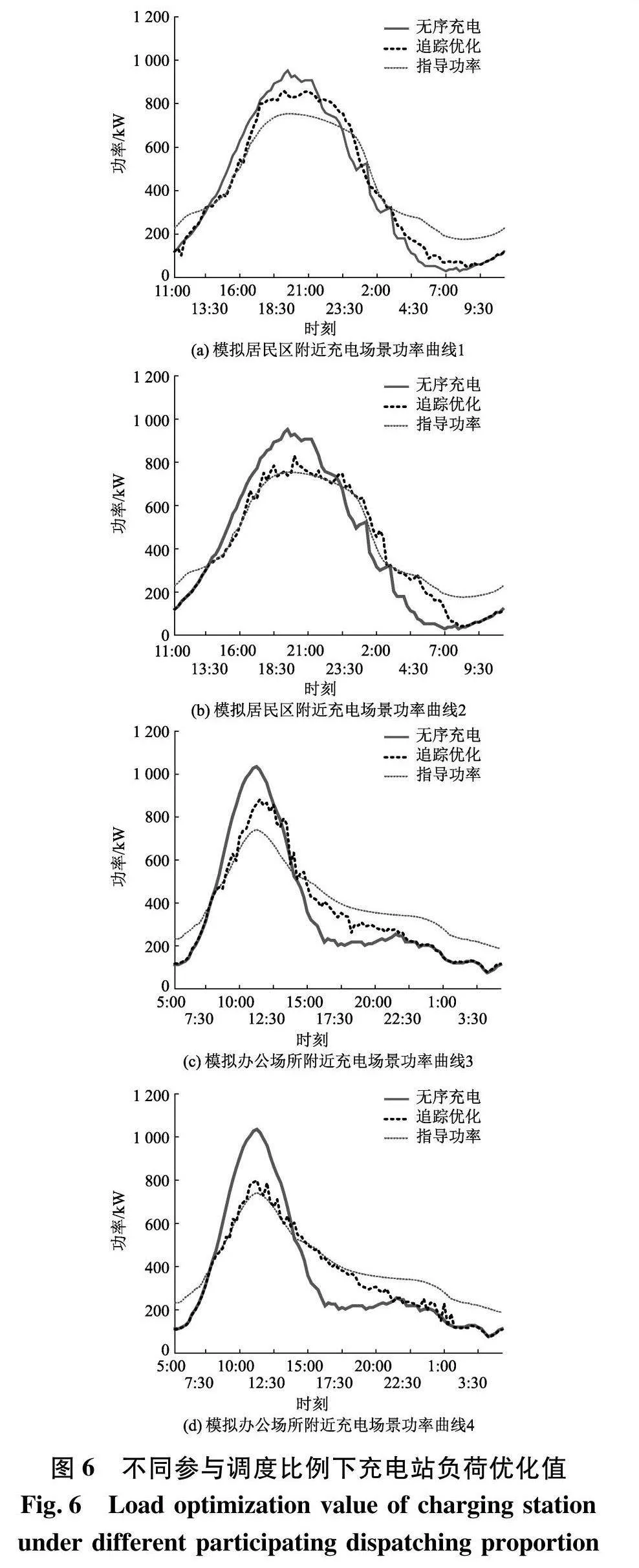
通过调整两个模拟充电场景中参与调度的电动汽车比例，得到充电站负荷的优化值如图6.

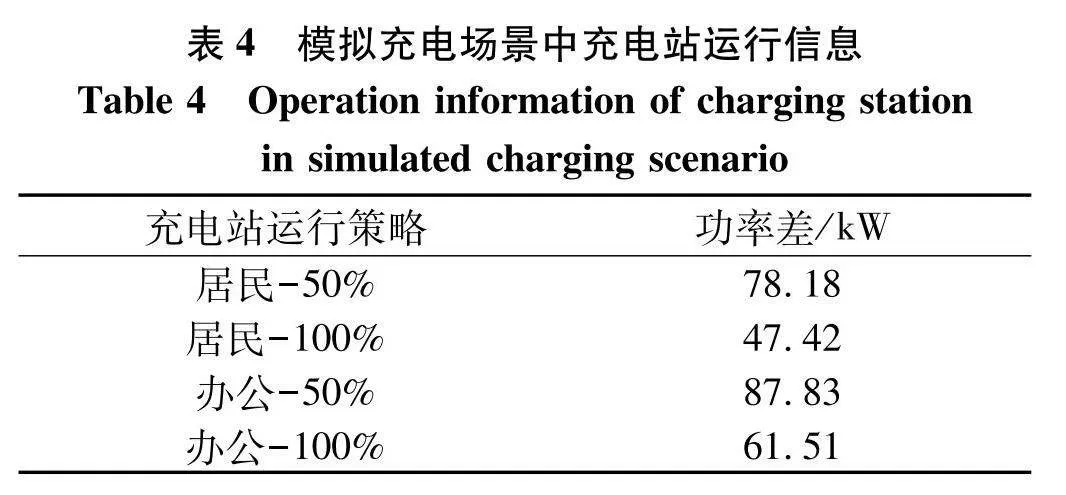
用负荷与功率指导曲线之间的功率平均差值表示追踪效果得到充电站运行信息如表4.

两个模拟场景中居民区与办公场所附近充电站无序充电下与指导功率的功率差分别为111.62、139.35 kW.结合表4中信息可以看出该方案能够实现功率追踪优化同时参与调度的电动汽车比例越高，调度效果越好.

第三个目标函数是综合考虑效益与功率追踪的优化，其目标函数为：

F=max∑96t=1P（t）×Δt×ΔFt－λ（P（t）－P（t）exp）2（17）

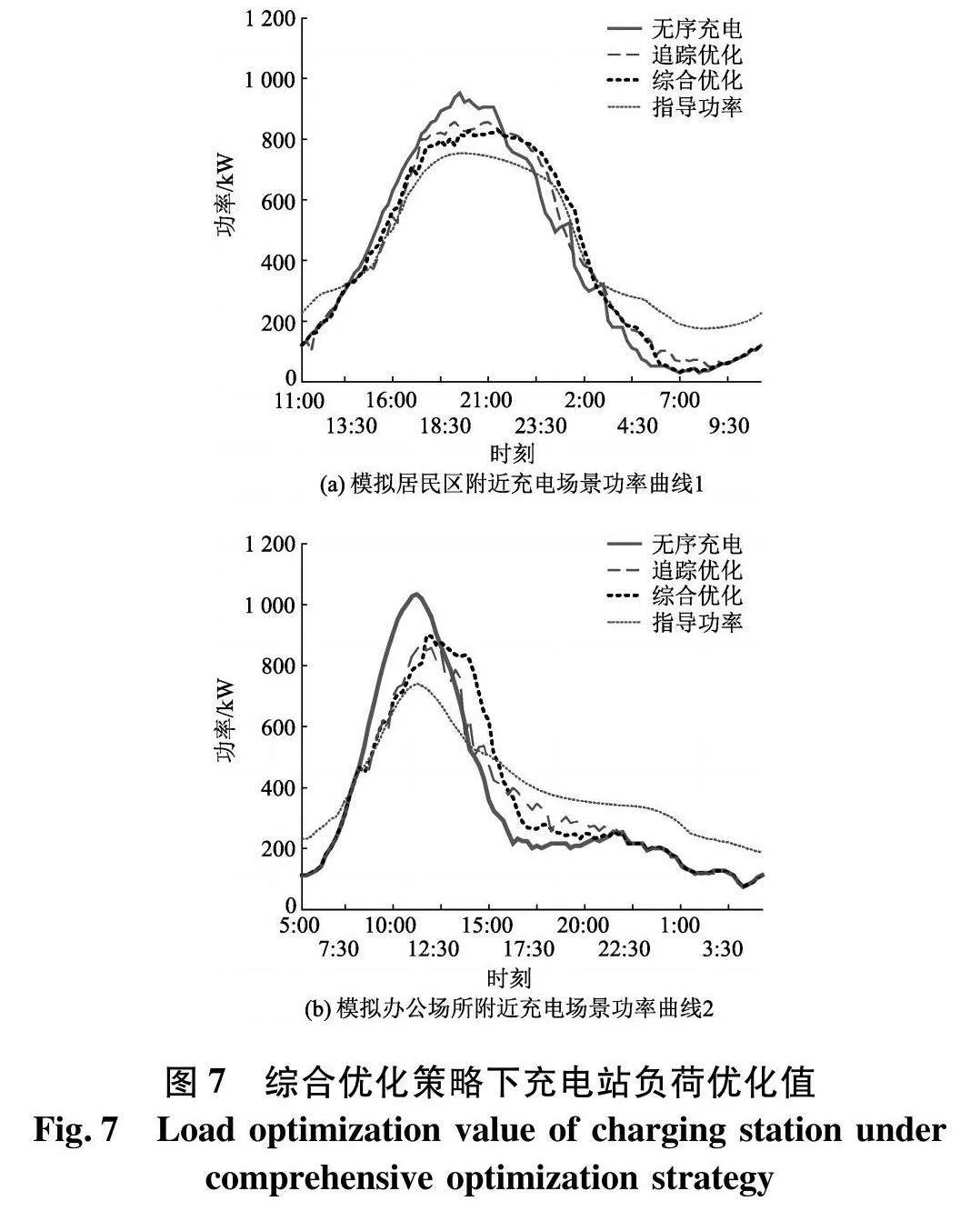
得到充电站负荷的优化值如图7.

充电站运行信息如表5.

结合表3、4中信息，可以看出该方案能够在实现功率追踪的同时提升充电站效益.

3"基于用户充电需求紧迫度与电网频率特性的功率分配方案

为了考虑电动汽车之间充电功率的平衡分配.一般可根据各电动汽车的最大充电功率使用注水法分配方案，文中提出了采用电网实时频率信号进行修正，从而使得电车充电站可以参与电网频率相应，对充电功率指令进行适度补偿.

根据充电裕度k并结合电网的频率指标将可调度的电动汽车分成3类，如表6.

由充电裕度k的定义可知：k越大其可调度的能力越强，对充电的需求紧迫程度越小.因此3类电动汽车对充电功率需求的紧迫程度依次下降.为了满足频率相应目标，可以在k的基础上按照电网实际频率进行修正，具体参数可根据需要在一定范围内（经测试0.2为佳）调整.

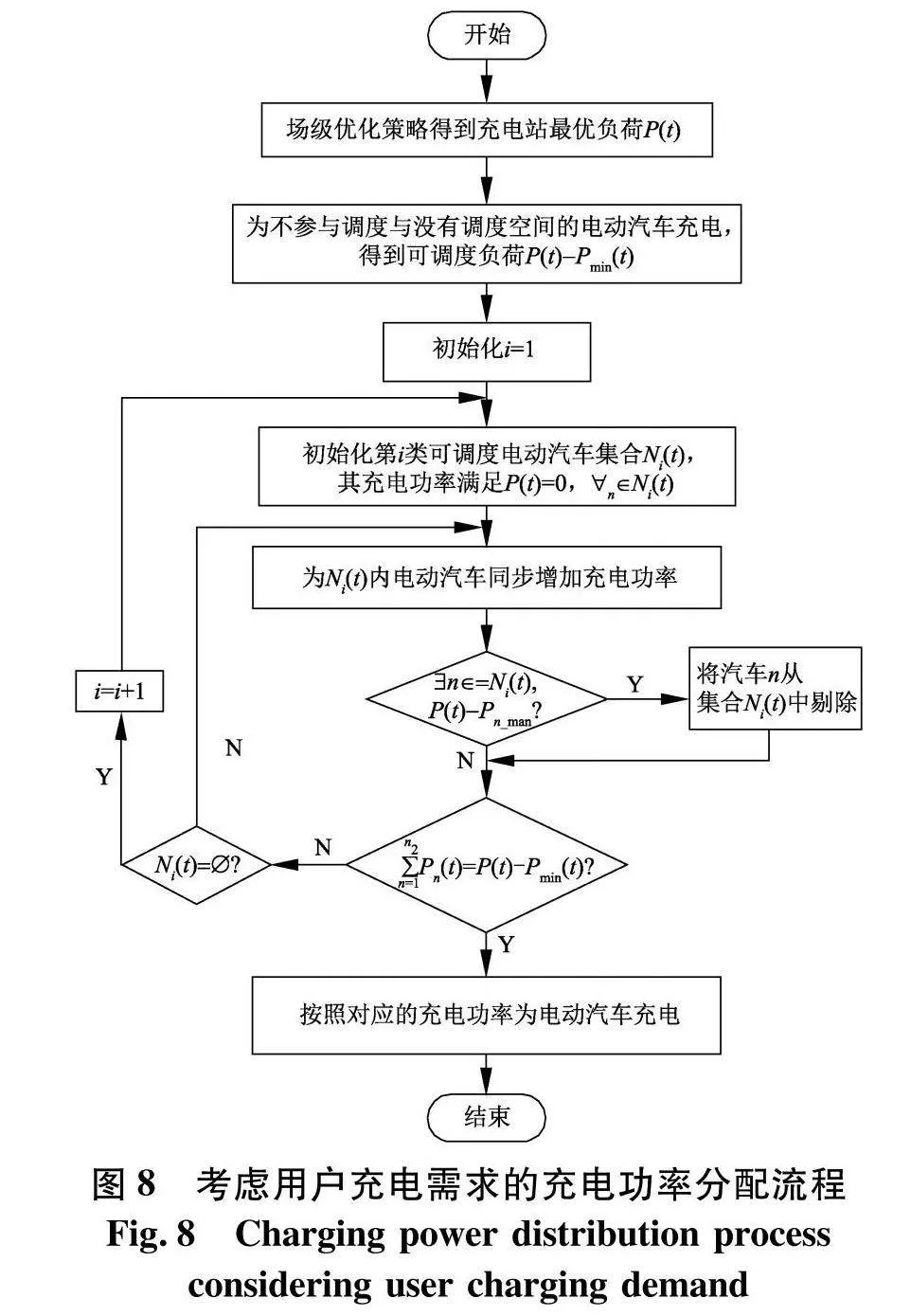
为了让对充电需求较为紧迫的车辆优先获得充电功率，制定了功率分配流程，如图8.

与原分配策略不同的是，该策略首先将电动汽车分为3个集群，分别为第一、二、三类电动汽车的集合.首先为第一个集群即对电量需求较为紧迫的电动汽车进行充电功率的分配，若分配完之后有多余的充电功率才对第二个集群内的车辆进行功率分配，同理第三类电动汽车充电功率分配需要在第二类完成之后有剩余功率时才进行.

与不考虑充电需求的功率分配方案进行对比分析，分别使用两种方法进行功率分配，从中选取4台电动汽车，其分到充电功率分别为0，15，1.5，3.5 kW，观察期荷电状态变化如图9.

其中一、二两台电动汽车在充电初始阶段属于第一类，调整后的分配方案使其在前期获得更多的充电功率.第二台电动汽车原先的分配策略下前期分配得到的充电功率较小使得后期必须以最大功率充电才能充满，从而失去了调度空间.第四台电动汽车由于提前完成了充电而失去了调度空间.

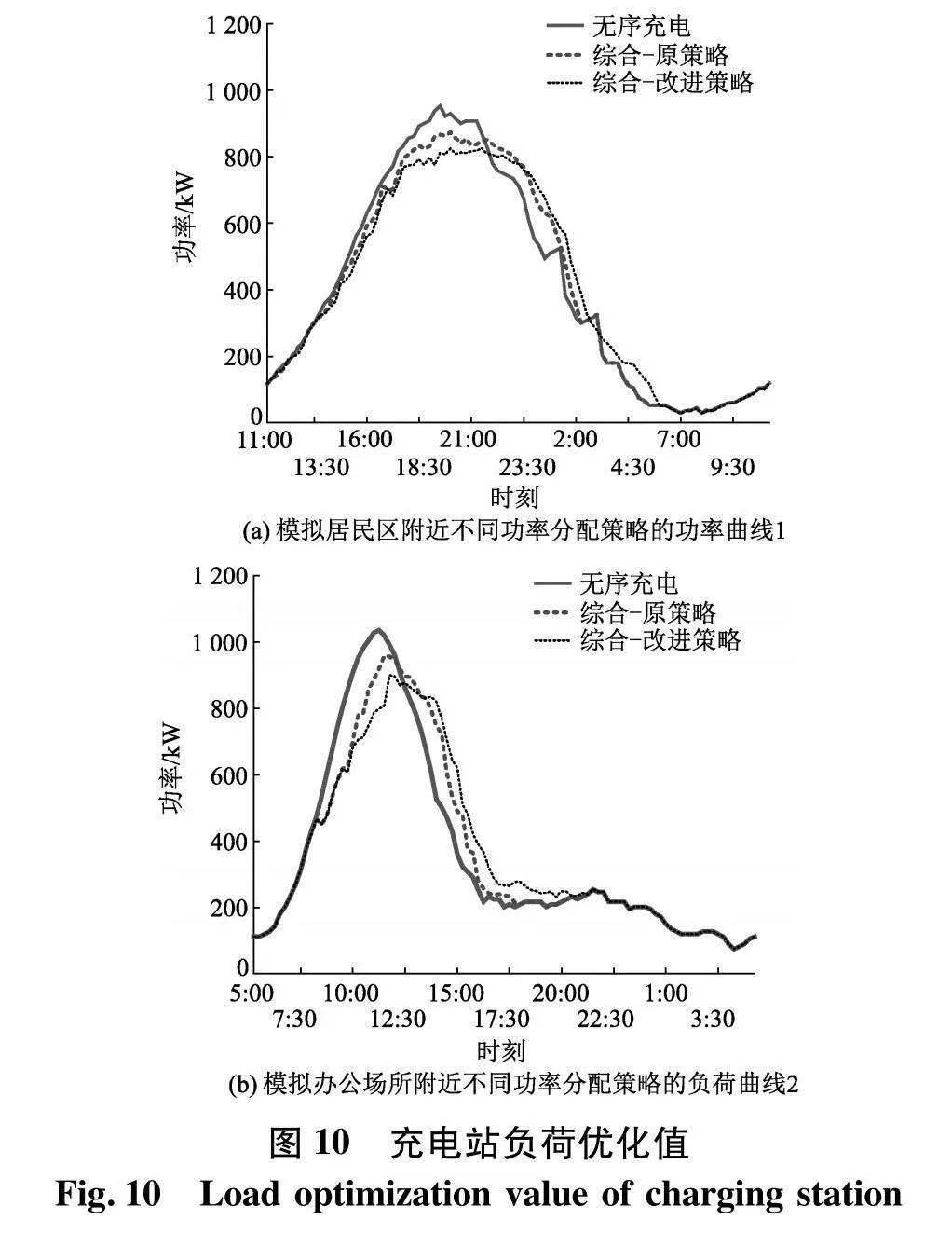
结合上层优化控制，以综合优化作为上层控制目标，分别采用调整前后的分配方案进行调度分析得到充电站负荷优化值如图10.

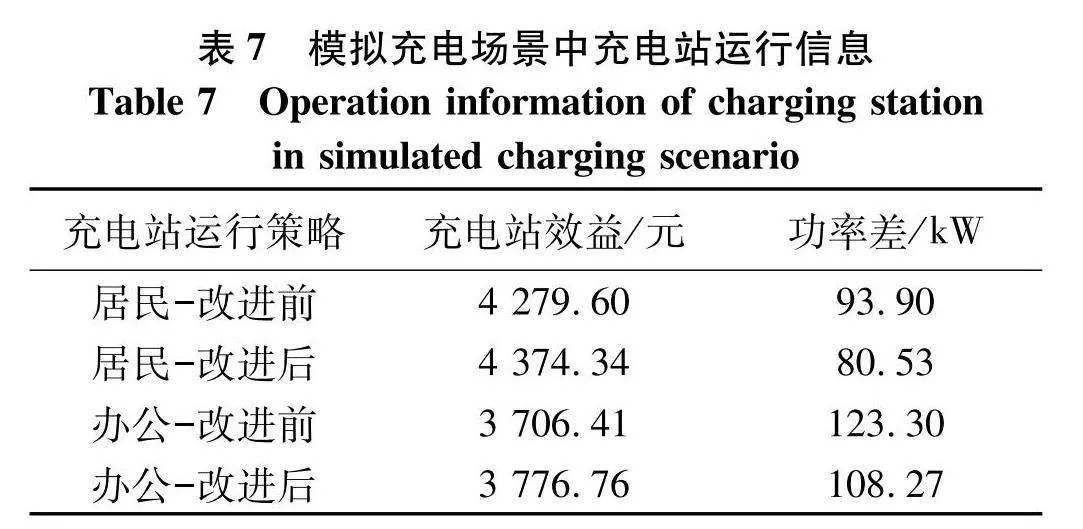
充电站运行信息如表7.

从表中信息可以得出改进后的综合优化策略在效益与功率追踪方面都比原策略好，这是由于在这两个模拟充电场景中，原先的充电桩控制策略使充电站的调度空间变得不合理.可以认为，在模拟系统中使用改进后的充电桩控制策略能够提高提升充电站场级调度的效果.

4"结论

针对充电站内电动汽车负荷，设计了一种分层实时调度策略.在上层优化中以效益优化、功率追踪、综合效益与追踪优化作为优化目标进行充电站负荷优化.而下层，以计及电网实时频率的用户充电需求紧迫程度作为考量调整充电功率分配方案，能够合理的为电动汽车进行充电并降低电网压力.该方案能够在较小的计算量下实现站内电动汽车实时充电策略制定，具有较好的工程可行性.两层优化的设计，通过下层充电桩与电车之间的优化，在满足充电需求的情况下，扩展了可调余量，为上层优化提供了更大的优化空间.

文中只研究了某种特定的充电功率分配方案，后续可在该框架下对诸多可行方案进行深入的对比研究，另外分配方案对上层调度的影响也有待于进一步深入研究.另一方面，文中的充电桩模型和方法目前没有考虑V2G功能，在后续研究中将对此进行探讨.

参考文献（References）

［1］"LIN X， SUN J， AI S， et al. Distribution network planning integrating charging stations of electric vehicle with V2G［J］. International Journal of Electrical Power and Energy Systems， 2014， 63： 507-512.

［2］"王新彦，赵培，桂天，等.轻型电动汽车新型制动能量回收系统的研究［J］. 江苏科技大学学报（自然科学版）， 2013， 27（2）：129-136.

［3］"DOUCETTE R T， MCCULLOCH M D. Modeling the CO2 emissions from battery electric vehicles given the power generation mixes of different countries［J］. Energy Policy， 2011， 39（2）： 803-811.

［4］"贺晓婧. 城市电动汽车规模化发展的环境和经济影响研究［D］.南京： 南京大学， 2020.

［5］"ANWAR M， MURATORI M， JADUN P， et al. Assessing the value of electric vehicle managed charging： A review of methodologies and results［J］. Energy and Environmental Science， 2022， 15（2）： 466-498.

［6］"阎怀东， 马汝祥， 柳志航， 等. 计及需求响应的电动汽车充电站多时间尺度随机优化调度［J］. 电力系统保护与控制， 2020， 48（10）： 71-80.

［7］"周萌. 考虑交通流量和网损的电动汽车充电站规划［D］. 宜昌：三峡大学， 2020.

［8］"DENG X， ZHANG Q， LI Y， et al. Hierarchical distributed frequency regulation strategy of electric vehicle cluster considering demand charging load optimization［J］. IEEE Transactions on Industry Applications， 2022， 58（1）：720-731.

［9］"江明， 许庆强， 季振亚. 基于时序差分学习的充电站有序充电方法［J］. 电力工程技术， 2021， 40（1）： 181-187.

［10］"孙近文， 万云飞， 郑培文， 等. 基于需求侧管理的电动汽车有序充放电策略［J］. 电工技术学报， 2014， 29（8）： 64-69.

［11］"柳也东. 基于需求响应的电动汽车有序充电定价策略［D］. 秦皇岛：燕山大学， 2019.

［12］"闫志杰， 张蕊萍， 董海鹰， 等. 基于需求响应的电动汽车充放电电价与时段研究［J］. 电力系统保护与控制， 2018， 46（15）： 16-22.

［13］"李苗苗. 面向电动汽车有序充电的控制策略研究［D］. 济南：山东大学， 2020.

（责任编辑：曹莉）