HPM视角下单元整体复习教学思考与实践

［摘 要］HPM视角下的单元整体教学和复习，有助于实现对教学内容的整体性认知。在“多边形的面积”单元复习中，通过整理单元学习框架、解决实际问题、概括一航策略、联系现实生活等活动，突出东西方数学文化中“出入相补”原理和“等底等高”命题相结合的转化路径，引导学生进行自主探究，达成对学习内容整体、一致的认识。

［关键词］HPM视角；单元整体复习；多边形面积

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）26-0020-04

《义务教育数学课程标准（2022年版）》指出，教学实施过程中“不仅要整体把握教学内容之间的关联，还要把握教学内容主线与相应核心素养发展之间的关联”。单元整体教学无疑是实现此整体性目标的重要手段，特别是单元整体教学视角下的复习课，更是具有提升学生认知水平，发展学生核心素养的重要价值。要想使单元整体教学与单元整体复习更加科学、合理，HPM（数学史与数学教育）视角下的教学分析、设计和实施是一条重要路径。如何借助HPM视角合理定位单元整体复习的目标？如何结合数学史、数学文化设计并开展单元整体复习？基于对这些问题的思考，笔者以“多边形面积整理与复习”为例，开展了教学设计与实践。

一、基于数学史料支持的单元整体复习定位

（一）“多边形的面积”相关内容的史料支撑

为了展现数学的发展历史，增加数学的人文“温度”，各版本教材中大都以“你知道吗？”等形式编排了片段式的数学史和数学文化内容。但这些数学史料没能形成统一的整体，在教学中的运用大多处于附加式、复制式等较低的水平层次，发挥的作用较为有限。对此，教师应搜集更为丰富的数学史料，围绕核心概念进行选择和加工，利用其设计并实施具有整体性和一致性的教学活动。

关于“多边形的面积”，在东西方数学文化中都能找到丰富的数学史料。我国传统数学文化注重实用性，由土地面积引出的面积计算公式是重要的多边形的面积研究对象。比如《九章算术》“方田”章就是围绕各种不同形状的土地面积展开研究并概括出了相应的计算公式，刘徽在为《九章算术》中的“圭田术（半广以乘正从）”做注时，提出了“半广者，以盈补虚为直田也”的观点，此即“出入相补”原理的具体表现。刘徽借助“出入相补”原理，用图形的分、合、移、补证明了不少数学恒等式，开创了中国古代数学中数形结合的独特的研究方法。在西方，古希腊数学的代表作《几何原本》被奉为经典，虽然它没有记载与面积计算直接相关的内容，但其中的“等底等高”命题与面积密切相关，是解决诸多面积计算问题的重要依据：将平行四边形和梯形都转化为三角形后再进行面积公式推导。

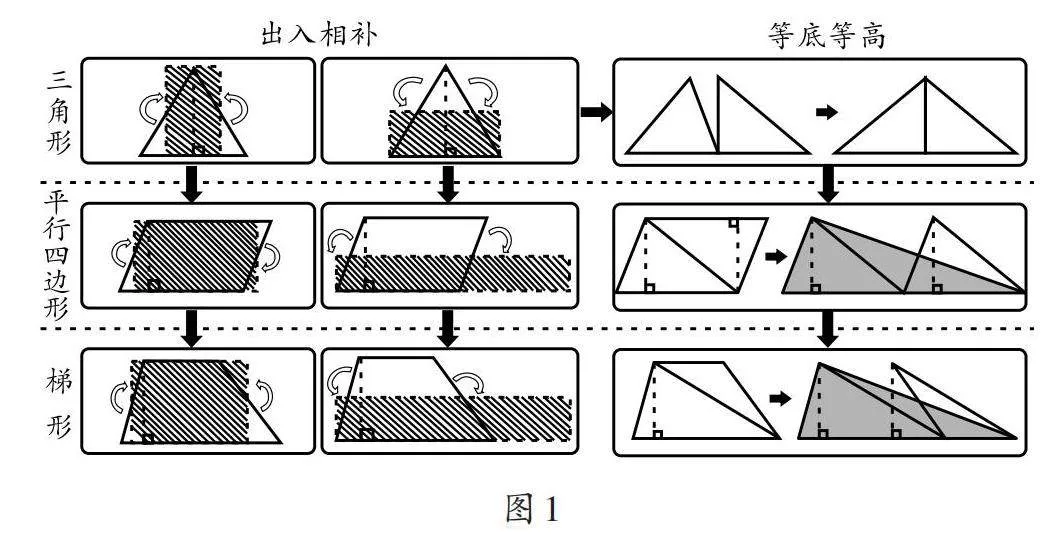
在HPM视角下的单元整体教学中，笔者设计并实施了三角形、平行四边形、梯形面积的整体性学习活动（如图1），希望在这三种多边形面积的学习过程中，学生能对东西方数学文化及多边形面积的转化方式有较为深刻的理解。有研究认为，平行四边形、梯形都可通过对角线分成两个三角形，因此可以用三角形面积计算公式来推导平行四边形与梯形面积的计算法则，然后可将圆无限细分成近似三角形，再同样以三角形面积之和来求圆的面积。这不仅印证了笔者已有的教学思路，还指出 了“多边形的面积”教学活动要兼顾后续“圆的面积”的教学。

（二）“多边形的面积”单元复习的目标定位

数学史、数学文化的价值在于它站在历史的高度俯瞰数学内容的发展脉络，能清晰地展现某一特定数学内容的过去、现在甚至未来。复习的意义在于温故知新：一方面是整理旧知，形成并完善知识体系和结构，另一方面是运用完善的知识脉络研究新的问题。因此，HPM视角能为复习活动的有效开展提供参照。

“多边形的面积”这一单元主要包括平行四边形的面积、三角形的面积、梯形的面积、组合图形的面积、不规则图形的面积等内容。从“多边形的面积”单元的内部结构来看，其可以分为“基本图形的面积”和“利用基本图形的面积解决问题”两部分。前者的目标是探索基本图形的转化方式，推导出基本图形的面积公式，并对此形成一致性理解；后者的目标是根据已掌握的转化方式和面积公式解决更多实际问题，发展应用意识和创新意识。从“多边形的面积”单元在整个小学阶段“平面图形面积”主题中所处的位置来看，“多边形的面积”这一单元起到了承前启后的作用：学生需要以它为基础（包括转化思想和面积公式）结合极限思想继续学习圆的面积。

为此，笔者尝试将“多边形的面积”单元复习与“组合图形的面积”“不规则图形的面积”两块内容进行整合，并将“整理与复习”作为第一个环节，以此充分发挥复习活动温故知新的作用（如图2）。从“多边形的面积”单元内部结构来看，该单元复习是温“三角形面积”“平行四边形面积”“梯形面积”之故，知“组合图形面积”“不规则图形面积”之新；从整个“平面图形面积”主题整体发展而言，该单元复习是温“直边图形面积”之故，知“圆的面积”之新。

二、依据数学文化主线的单元整体复习实施

（一）总结回顾，整理学习内容

复习课的首要任务是梳理前期的学习内容。在数学史、数学文化支持下的单元整体教学将构建清晰的学习路径，这能使学生的学习事半功倍，复习也会变得更加高效。在“多边形的面积”单元中，学生虽然能够在各类多边形转化和面积公式推导的过程中，结合东西方文化中相关的史料对多边形的转化路径有清晰的认识，但是由于这些内容通常是分散的，因此很有必要通过整体呈现的方式再次唤醒学生的记忆。

课始，笔者请学生回顾本单元实际的学习路径，将其与教材中的学习路径进行比较，并说说学习过程和心得体会。有学生经过比较后指出，教材中的顺序和方法虽然比较简单和直接，但也相对单一；课堂上的学习过程更加丰富有趣，按照三角形、平行四边形、梯形的顺序来学习，整个单元都围绕“出入相补”和“等底等高”两种方法转化图形，不仅非常巧妙，而且有助于加深理解。也有学生提出，三角形可以转化成长方形，平行四边形可以转化成长方形和三角形，梯形可以转化成长方形、三角形和平行四边形，转化的方法越来越多。还有学生提出，按照《九章算术》的顺序，先学习三角形，再学习梯形，最后学习平行四边形，也是可以的。最后，学生还发现，虽然学习的过程是按照一定顺序进行的，但在学完了几种平面图形的面积公式之后，它们之间是可以互相转化的。在整体回顾的过程中，学生进一步明确了两条转化路径，全面、立体地感受了已知多边形之间的关系，并能用辩证、发展的眼光看待这些关系。

（二）问题解决，提升应用能力

基于数学史、数学文化视角的单元整理与复习，是希望教学的主线与脉络能有更好的延续。这样，在运用已有知识、技能、方法、策略解决新问题的过程中才能体现HPM视角下的单元整体教学的价值。通过对前期学习内容的整理，学生对多边形的两条转化路径有了更加清晰的把握，此时需要通过解决实际问题来给学生提供应用的机会，促使学生在问题解决的过程中提升分析和决策能力。

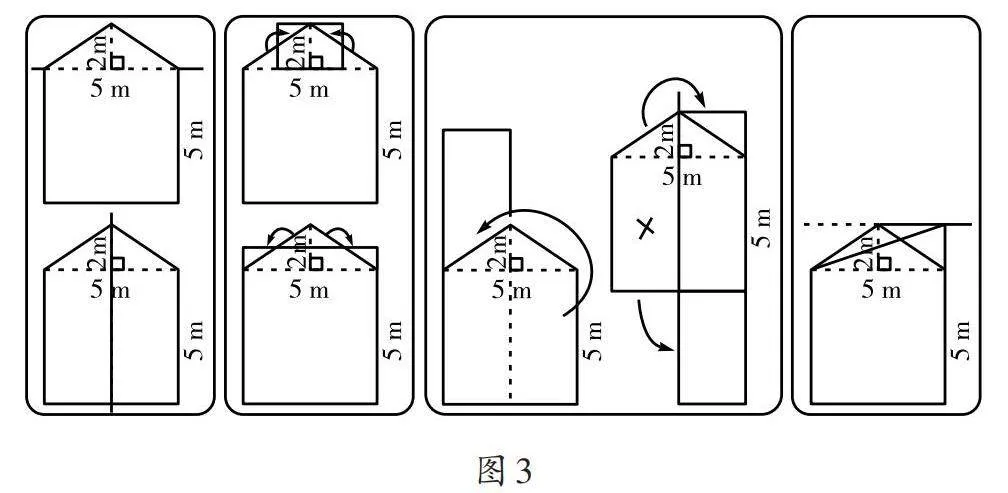
笔者出示“房屋侧面图”，请学生在转化的基础上计算其面积。学生根据图形的特点，采用了常见的“分割求和”“出入相补”原理和“等底等高”命题支持下的转化方法，对图形进行了合理转化，并计算出了它们的面积。笔者在此基础上组织学生对不同的转化方法进行分类整理，凸显同类方法之间的共同特点（如图3）。这一环节既考查了学生具体问题具体分析的能力，也充分体现了数学文化背景下的学习活动成果的应用价值。

（三）思维进阶，达成深度理解

在以数学文化背景下的单元整体教学中，复习课的目标就不能停留在简单应用的层面，而应借此进一步发展学生的思维水平，使学生概括出图形面积计算的一般策略。为此，在简单的组合图形面积计算的基础上，还应借助特定的素材，让学生体验转化思想、转化方法的灵活运用。在组合图形中，因为可以从上下、左右两个不同角度将“筝形”分割成不同的三角形，所以“筝形”是考查学生综合能力的有效载体。

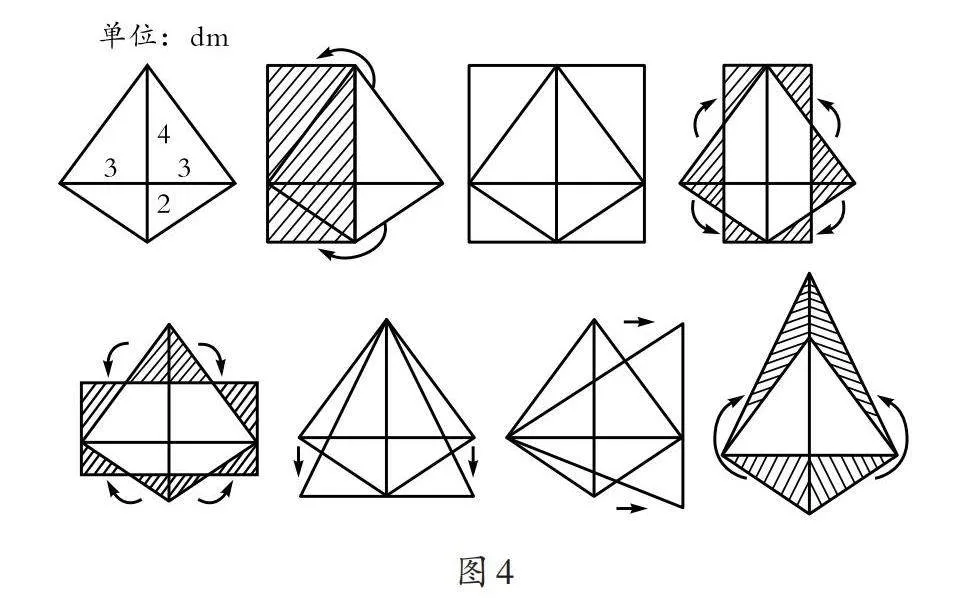
笔者出示“筝形”及相关的数据，请学生把它转化成已知图形并进行面积计算。学生探究得出了多种有效方法，包含了“一般割补法”“出入相补法”“等积变形法”等（如图4）。在教师的引导下，学生还发现，不管何种转化方式，最终都是将“筝形”转化为长方形或三角形两种基本图形，这也是解决此类问题最为便捷和有效的方法。在比较、概括转化结果及计算的过程中，学生还得出了计算“筝形”面积的通用计算方法（对角线的乘积除以2），以及这种通用计算方法与各转化方法之间的对应关系。于是，通过“筝形”问题，学生对转化思想及其具体策略的理解达到了兼XXV1JG4bhsVPRs19ych0SA==顾过程与结果的水平，这将对后续研究其他平面图形面积起到极大的推动作用。

（四）拓宽视野，延续探究思路

数学学习，既要注重知识内部的发展，也要关注数学与现实世界的联系。若能通过特定的情境与素材将这两者有机结合起来，不但能解决实际问题，还能引出后续的学习内容。比如浙江省地图作为一个不规则图形，与六边形比较接近，是一个非常有价值的素材，通过对其进行研究，可以优化图形转化的方案，凸显平面图形之间的内在联系。

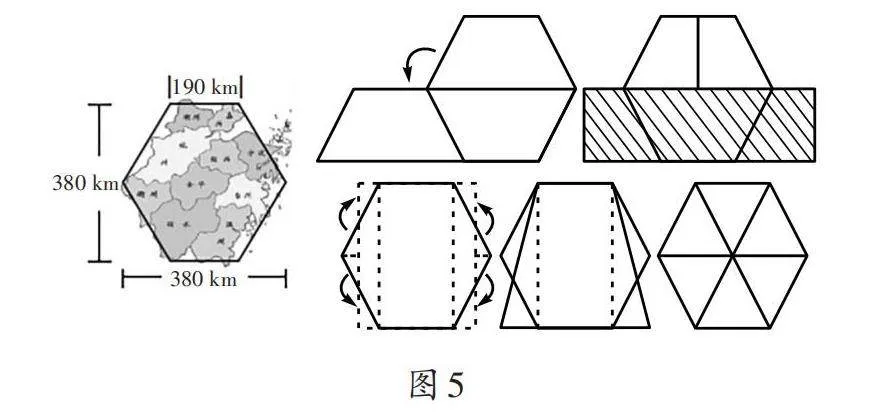
笔者出示浙江省地图，请学生说说可以采用什么策略来计算浙江省的面积。学生提出把浙江省地图近似地看作六边形，但需要知道相关的数据。笔者在浙江省南北、东西的最大距离（均为450 km）的基础上，给出将地图调整为近似六边形后的数据（设定南北、东西的距离均为380 km），请学生估算它的面积。学生运用计算“房屋侧面图”“筝形”等图形面积中获得的策略、方法和经验，通过“分割求和”“出入相补”“等底等高等积变形”等途径（如图5），计算出了近似面积（108300 km²）。此时，笔者出示浙江省实际面积（105500 km²）与学生计算的结果进行比较，以增强学生的自信心。

活动最后，笔者将“筝形”与正六边形联系在一起，得到了正十二边形（如图6），学生由此联想到了圆这一曲边图形，体会到了多边形与圆之间的关系，心中埋下了探究的种子。

三、立足文化育人目标的单元整体复习反思

基于HPM视角的单元整体复习，对数学史与数学文化的应用、单元整体目标的达成及学生主体地位的体现，都起到了积极的作用。

（一）促进学生思维的深度发展

数学史、数学文化融入数学课堂教学活动，不是将数学史料作为课堂教学中锦上添花的点缀，而是希望它能成为学生真正的内在需求，成为学生深度学习的有效载体和手段。在融入数学文化的单元整体教学的基础上，在“多边形的面积”单元复习课中，东西方数学文化下的转化思想成为学生有力的思想武器。在自觉运用两条转化路径解决问题和实践创新的过程中，学生的思维得到了进一步的发展，这正是HPM视角下的课堂教学追求的目标。

（二）达成学习内容的整体理解

在教学设计和实施过程中，不论是融入数学史，还是开展单元整体教学，都是为了更好地借助两者的优势实现学生对学习内容的整体理解，为学生呈现平面图形面积学习和研究的全景。在“多边形的面积”单元复习过程中，学生通过整理单元学习框架、运用多种方法解决问题、研究解决实际问题等活动，对整个单元的学习内容有了全面的认识；通过自主探索和迁移运用，不仅掌握了知识技能，也使转化思想在心中扎根。

（三）实现教学主体的有效转变

在HPM视角下的单元复习课将教学活动从“教”的立场转变为“学”的立场，学生主动参与活动，实现了知识、技能、能力、素养等方面的提升。数学史、数学文化的融入，打破了学生对数学的固有感受和刻板印象，让冰冷的数学变得有温度，学生就能够像数学家一样经历数学知识的整个学习和探究过程，学习自然就成为学生的自主行为。

【本文系2020年度教育部人文社会科学研究青年基金项目“多路径数学科普的构建及其对少数民族学生数学观的影响研究（20YJC880117）”阶段性成果。】

（责编 金 铃）