HPM视角下单元起始课的教学思考与实践

［摘 要］数学史中蕴含的数学发展脉络，对于梳理教学顺序和提炼教学主线具有重要的参考价值，是单元起始课设计与实施的重要依据。从HPM视角梳理教学内容的顺序，以达到逻辑序、历史序和认知序“三序合一”的目的；从HPM视角提炼教学主线，以形成围绕特定主题的系列化、结构化数学知识体系和学习路径；从HPM的角度设计与实施单元起始课的教学活动，为核心思想方法提供载体，体现核心思想方法的价值，为单元后续内容的学习提供思路和线索。

［关键词］HPM；三角形的面积；单元起始课

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）26-0006-05

《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）特别注重核心素养培养的整体性落实，提出“要通过单元整体教学设计体现数学知识之间的内在逻辑关系，以及学习内容与核心素养表现的关联”。在单元整体教学的设计与实施过程中，单元起始课的作用非常重要，它是整个单元的知识技能、思想方法的起点，为后续内容的学习指明了方向。数学史作为蕴含数学发展脉络的重要资源，对于梳理教学顺序和提炼教学主线具有重要的参考价值，因此，它也是单元起始课设计与实施的重要依据。为此，笔者以数学史料为参照，将“三角形的面积”作为“多边形的面积”单元起始课，以HPM（数学史与数学教育）视角进行教学顺序分析、教学主线提炼及教学活动设计与实施。

一、分析教学顺序，明确教学起点

数学教材是数学学习的重要资源与载体，但是往往受限于篇幅容量和表现形式，只能静态呈现部分重要的结论，并且这些内容一般都侧重于知识点的逻辑顺序。然而，教材编排应平衡学生学习和学科体系之间的关系，既要关注学科内容的整体性，也要考虑学生学习的心理特征，不要简单地按学科体系的结构化顺序编排。数学学习应建立在充分经历和体验的基础上，学习过程应尽可能同时兼顾数学知识内部的逻辑顺序、数学知识产生和发展的历史顺序，以及学生认知过程中的心理顺序。从HPM视角分析教学内容的顺序，是达到“三序合一”目标的有效手段，并且有助于明确单元起始课的内容。

以“多边形的面积”单元为例，国内大部分教材都是按照“平行四边形→三角形→梯形”的顺序编排，国外一些教材（如美国Sadlier-Oxford版、新加坡Marshall Cavendish版等）则采用“三角形→平行四边形→梯形”的顺序编排。可见，平行四边形、三角形和梯形这三个内容之间并无绝对严格的先后顺序。

从教学内容的逻辑顺序来看，采用先平行四边形后三角形的顺序，是考虑到了平行四边形与长方形在形状上有较高的相似度，将平行四边形转化为长方形是有充分的逻辑依据且便于操作的。同时，以《几何原本》中的命题Ⅰ. 34（平行四边形的对边相等、对角相等，对角线平分该平行四边形）为依据，借助平行四边形与三角形的关系，有助于通过平行四边形的面积进一步研究三角形的面积。但是，《几何原本》命题Ⅰ. 41（如果一个平行四边形和一个三角形既同底又在两条平行线之间，即两者的高相等，则这个平行四边形的面积是这个三角形的面积的两倍）又表明，若已知三角形的面积，也可以得出与其等底等高的平行四边形的面积。

从教学内容的历史产生顺序来看，我国传统数学名著《九章算术》及其刘徽注中关于多边形面积的编排顺序依次为“方田（长方形）、圭田（等腰三角形）、邪田（直角梯形）、箕田（等腰梯形）”，其中并无平行四边形。由长方形面积的计算方法得到三角形面积的计算方法，古已有之。

从学生的认知心理顺序来看，虽然把平行四边形的面积安排在长方形、正方形的面积之后，有利于学生根据两者形状的相似性进行转化，但也正因为这个相似性，容易造成负迁移，使学生误认为平行四边形面积的计算方法是邻边相乘，而将三角形的面积安排在长方形的面积之后，就可以避免这个问题。

当数学知识在教材中以逻辑顺序呈现，而逻辑顺序不符合学生的心理认知顺序，未能凸显知识的必要性时，就需要从HPM的视角来设计教学。郭书春通过对《九章算术》的研究发现，三角形的面积公式在刘徽的面积理论中起着核心作用。他认为“刘徽的面积理论是一个以长方形面积为出发点，以三角形面积为核心，运用出入相补原理和无穷小分割方法的有机整体”。陈敏、许含英等认为，平行四边形、梯形都可通过对角线分成两个三角形，因此可以0d5443115e43aee3468d8aac32f6d23e2332c759d0d1b9adf4d4a203da1ea192用三角形的面积公式推出平行四边形与梯形面积的计算方法。

因此，为了尽可能使数学知识内部的逻辑顺序、数学知识产生的历史顺序、学生学习过程中的心理顺序三者协调一致，并揭示知识的内在联系，充分体现单元起始课作为教学起点的价值，将“三角形的面积”作为“多边形的面积”单元的核心内容与起始课是一种可行且有益的尝试。

二、提炼教学主线，锁定核心内容

《课程标准》指出，为实现核心素养导向的教学目标，不仅要整体把握教学内容之间的关联，还要把握教学内容主线与相应核心素养发展之间的关联。因此，教学主线是沟通教学内容与核心素养之间的媒介。不同社会文化背景下的数学学科在其漫长的发展过程中，经过不断地去粗取精，形成多个围绕特定主题的系列化、结构化数学知识体系与核心线索，这一核心线索必定是贯穿于同一主题中的各个内容的。因此，在数学课堂中引入数学史，有利于在单元起始课中体现教学主线，为学生在后续学习的过程中不断加深对教学主线的理解奠定基础。

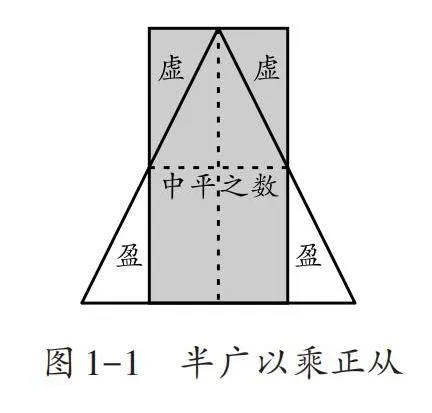
以“多边形的面积”单元中的“三角形的面积”一课为例，在《九章算术》中，关于等腰三角形面积计算的方法“圭田术”称“半广以乘正从”，即“底的一半乘高”。刘徽在为其做注时称：“半广知，以盈补虚为直田也。半广乘从，以取中平之数，故广从相乘为积步。”意思是，之所以取底的一半，是为了通过“以盈补虚”把三角形转化成长方形，并且底的一半其实就是上底与下底的平均数（这里可以理解为把三角形视作特殊的梯形，因此“中平之数”即上底与下底的平均数），也就是现在所说的中位线。因此，三角形的面积公式也就和长方形的面积公式“长×宽”保持一致了（如图1-1）。此外，刘徽也提出了自己的计算方法——“半正从以乘广”，即“高的一半乘底”，同样也采用“以盈补虚”的策略，把三角形转化成长方形，并借助长方形的面积计算方法来计算三角形的面积（如图1-2）。此外，《九章算术》及其刘徽注的“邪田术”“箕田术”“圆田术”“环田术”都体现了对平面图形面积计算整体性和一致性的极致追求。虽然《九章算术》中的“圭田术”和刘徽的“以盈补虚”策略是以等腰三角形为对象的，但实际上它们适用于计算任意三角形的面积。因此，通过“以盈补虚”的策略化归为“广从相乘”是三角形的面积及后续推导其他平面图形的面积公式的重要途径。

西方古典数学名著《几何原本》注重对数学对象的理性思考，几乎不涉及实际问题的解决，因此也没有与图形面积计算直接相关的内容，但其中有一些重要命题与图形的面积有关。除上文提到的命题Ⅰ. 34和命题Ⅰ. 41涉及等底等高的平行四边形与三角形之间的面积关系之外，命题Ⅰ. 35、命题Ⅰ. 36、命题Ⅰ. 37、命题Ⅰ. 38也都与图形的面积有关。其中，命题Ⅰ. 35是“同底且在两条平行线之间的平行四边形的面积相等”，命题Ⅰ. 36是“等底且在两条平行线之间的平行四边形的面积相等”，这两个命题都是关于平行四边形面积的，一般可将这两个命题统一为“等底等高的平行四边形的面积相等”；命题Ⅰ. 37和命题Ⅰ. 38都是关于三角形面积的，两者关系与命题Ⅰ. 35和命题Ⅰ. 36之间的关系类似，可以概括为“等底等高的三角形的面积相等”。在教材中，这些命题一般被用于解决具体的面积问题，然而，其教学价值远非如此，如“等底等高的三角形的面积相等”还可用于平行四边形、梯形的面积公式的推导。因此，在“三角形的面积”一课教学中，还应结合具体问题，使学生体会“等底等高的三角形的面积相等”这一特征，并能对其进行灵活应用，为后续运用这一命题进行多元化的图形转化和公式推导提供方法支持。

从HPM视角出发，结合东西方数学史料的分析可以发现，转化思想是“三角形的面积”及“多边形的面积”单元的教学主线。围绕转化思想这一教学主线可以得到“以盈补虚（出入相补）”和“等底等高的等积变形”两条明确的路径，这两条路径的有效推进与协同作用是教学多边形面积的重要保障。可见，以历史上的既成事实作为提炼教学主线的重要参照，对教学内容进行整体分析，可以使单元整体教学活动的逻辑更加清晰，同时也提升了单元起始课的教学定位。

三、实施教学活动，体现核心价值

转化思想是一种重要的数学思想方法，运用转化思想的目的在于将陌生的对象转化为熟悉的对象，将未知的问题转化为已知的问题，从而有效地解决问题。在“多边形的面积”单元中，转化思想主要表现为“以盈补虚（出入相补）”和“等底等高的等积变形”两种形式。在教学单元起始课“三角形的面积”时，应紧紧围绕转化思想的两种表现形式开展教学活动，以使其能在整个单元中起到提纲挈领的作用。

（一）初步探究，提供转化思想的恰当载体

长方形的面积是学习平面图形面积的基础，长方形也是三角形转化的对象。因此，有必要对长方形的面积公式进行适当复习，并以此引出《九章算术》中的“方田术”（长方形面积的计算方法），通过对古今方法的比较，使学生体会数学知识的历史传承。需要注意的是，即使学生有了长方形的面积公式这个基础，教师要想让学生自主推导出三角形的面积公式也是有一定难度的。因此，为了遵循从特殊到一般的认知规律，并与《九章算术》中的内容顺序保持一致，同时也是从便于操作探究的角度考虑，笔者选择了等腰三角形作为引导学生感受转化思想的载体。

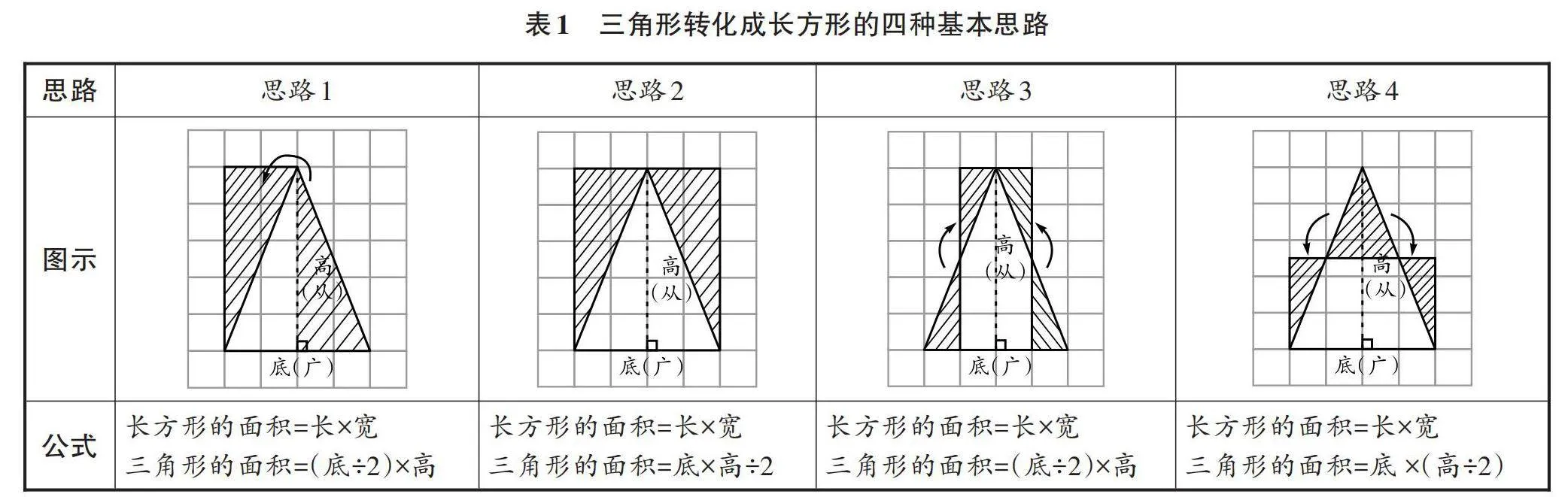
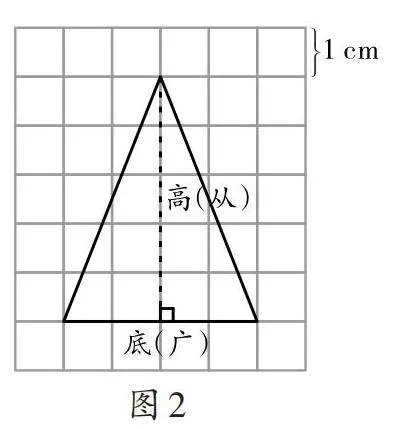
笔者在引导学生复习长方形面积公式的基础上，请学生解读《九章算术》中的“方田术”——“广从步数相乘得积步”，将广与长、从与宽联系起来，以便更好地解读“圭田术”。随后，笔者出示等腰三角形（如图2）及刘徽对“圭田术”的注解“以盈补虚为直田也”，请学生尝试解读这句话的意思。学生结合等腰三角形的图示，认为这句话的意思是指通过“移多补少”的方法把三角形变成长方形。笔者对此予以肯定，并请学生按照这一思路，以小组合作的形式，通过画图将三角形进行转化，并根据转化前后图形之间的关系，得出等腰三角形的面积公式。通过不同的转化操作，学生得到了不同的转化结果和面积公式（见表1）。在师生共同评价的过程中，笔者围绕问题“为什么要除以2？”请各小组解释自己的操作活动，让学生将具体的操作与抽象的符号联系起来，帮助学生进一步深入理解转化过程和结果。

（二）迁移运用，理解转化思想的重要价值

等腰三角形作为特殊的三角形，有助于学生迅速找到转化思路。学生在领悟了“以盈补虚”策略后，还需要由点及面进一步验证任意三角形都能通过“以盈补虚”策略转化成长方形。如此，研究的思路也遵循了从特殊到一般的规律，并使结论更具严谨性和普遍性。

在运用“以盈补虚”策略推导出等腰三角形的面积计算方法后，笔者追问：“这样得到的面积公式是否能运用于所有三角形？”学生指出“需要用一般的三角形去验证计算方法的正确性”，并经过操作验证发现任意三角形都能通过“以盈补虚”策略转化成长方形，充分体现了转化思想在数学中的重要意义和价值。这样的活动设计与实施，既在单元起始课中根植了能统领整个单元的转化方法，又让学生感悟到从特殊到一般的研究策略，并且培养了他们科学严谨的学习和研究态度。

（三）古今对照，了解转化思想的历史传承

教学过程中有意识地选用中华优秀传统文化中的实际问题及其解决方法作为整个单元系列活动的起点，有助于学生了解数学知识技能、思想方法的发展过程和特点。在此基础上，借助古今对照，可以引导学生与古代伟大数学家进行跨越时空的“对话”，从而体会思想方法的历史传承，提升学习兴趣和信心。这充分体现了数学史“转知为智”“以文化人”的教育功能。

在学生对三角形的几种转化思路有了深入的理解之后，笔者出示《九章算术》及其刘徽注中的两种“圭田术”——“半广以乘正从”和“半正从以乘广”，请学生说说两种方法分别对应表1中的哪种转化思路，它们之间有什么异同。学生结合这两种古代方法的语言描述及同伴操作时所作的图示，确定了它们分别对应表1中的思路3和思路4，它们的不同点是分割的方式有所区别，但它们的目标都是通过“以盈补虚”策略将三角形转化成长方形。这样的辨析活动有两方面作用：一是使学生了解关于三角形面积的知识及转化思想在历史上的表现形式，感受古人应用图形特征的巧思妙想，同时也为后续形成多边形转化的主线提供了参照；二是帮助学生看到古代数学家的研究方法和自己或同伴的探究方法有着异曲同工之妙，知道了数学知识不是凭空产生的。至此，数学文化通过不同的形式得到了不断延续和传承，进一步增强了学生数学学习的参与感和获得感。

（四）中外对比，感受转化思想的多元形式

转化思想在数学学习中具有重要作用，其内涵非常丰富，就图形面积问题而言，至少包括“以盈补虚（出入相补）”和“等底等高的等积变形”两种方式，后者是“多边形的面积”单元的重要内容。因此，笔者以问题解决的形式，在图形面积的比较中帮助学生认识这一转化方式。

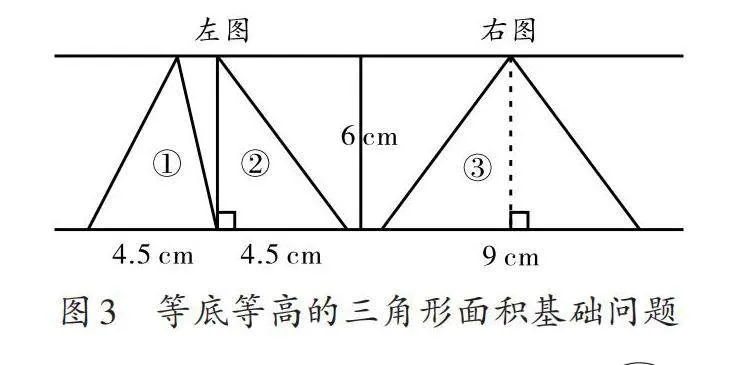
笔者提供一组平行线之间等底等高的两个三角形①②（如图3），请学生判断两个三角形的面积是否相等。学生给出两种不同的判断方法：一是通过具体计算得到两个三角形的面积后进行比较；二是根据三角形的面积公式及其中的底和高两个数据直接判断。于是，笔者出示《几何原本》中的命题Ⅰ. 38，并请学生判断图3的①②两个三角形的面积之和与三角形③的面积的大小关系。此时，大部分学生根据“等底等高的三角形面积相等”这一命题对左图进行转化，发现左图两个三角形可以合并成一个大三角形，且面积与右图三角形的面积相等。

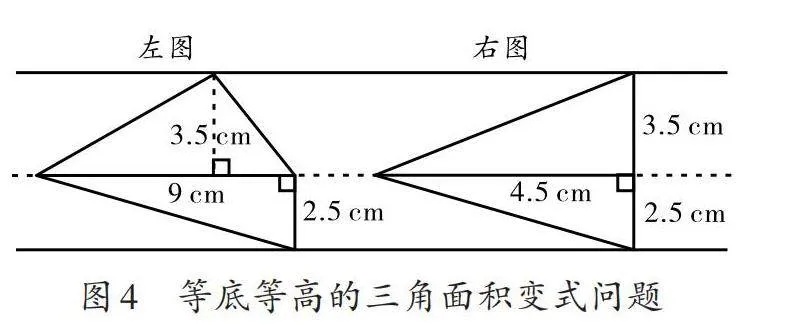
在此基础上，笔者通过变式练习（如图4）帮助学生进一步理解“等底等高的等积变形”在解决问题中的重要作用。学生发现，根据“等底等高”命题，移动左图上方钝角三角形的顶点，可以将其变成与原来面积相等的直角三角形，因此图4中左、右两图的面积也是相等的。通过上述问题，学生不仅深刻地理解了“等底等高的三角形面积相等”这一命题，而且体会到了转化思想的不同表现形式，为后续平行四边形、梯形和组合图形的转化提供了思路。

单元起始课的价值不仅是让学生掌握知识，还应充分体现学习的必要性，以知识为载体，全面揭示数学知识背后的育人价值，提升课程与教学的立意与价值。HPM视角下的单元起始课以数学史料为素材，将其转化为能够直接促进学生数学学习的一系列活动，并按照一定的逻辑构建一个让学生经历问题解决全过程的学习结构，促使学生思维生长。同时，学生的思维、情感、态度与价值观得以深度激活与释放，学生真正经历了有意义的学习过程。因此，在HPM视角下有目的、有计划地设计单元起始课，发挥其在单元整体学习活动中的导航作用，有助于凸显教学主线，完善学生的认知结构，使学生对单元学习建立总体认知。

［ 参 考 文 献 ］

[1] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[2] 马云鹏.基于结构化主题的单元整体教学：以小学数学学科为例[J].教育研究，2023（2）：68-78.

[3] 陈飞.中国特色的HPM理论：将数学历史融入数学教学：汪晓勤教授访谈录[J].中学数学教学参考，2019（7）：7-12.

[4] 郭书春.古代世界数学泰斗刘徽[M].济南：山东科学技术出版社，2013.

[5] 陈敏，许含英.三角形和梯形面积教学研究[M].北京：教育科学出版社，2014.

【本文系2020年度教育部人文社会科学研究青年基金项目“多路径数学科普的构建及其对少数民族学生数学观的影响研究（20YJC880117）”阶段性成果。】

（责编 金 铃）