基于VBEM的一致受限字典织物图像重构模型

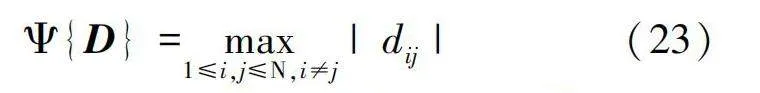
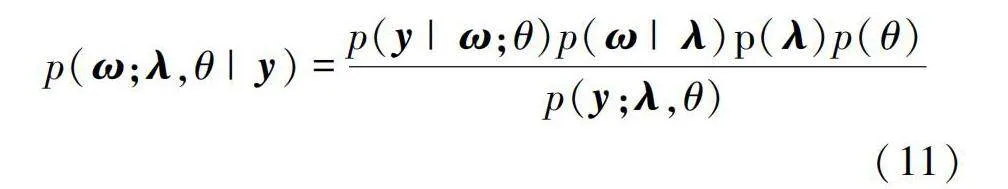
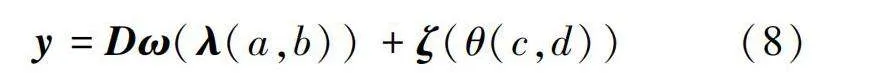
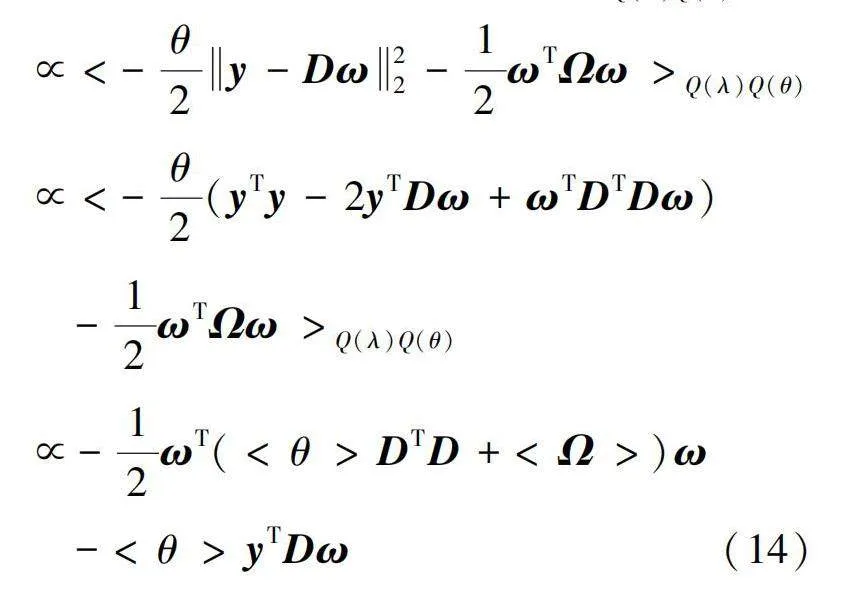
摘 要：针对传统稀疏贝叶斯算法中字典列之间较强的相互一致性导致的重构性能下降问题，提出了一种基于变分贝叶斯期望最大化的一致受限字典织物图像重构模型（CCD-VBEM）。考虑织物图像的真实应用场景，采用多层先验的稀疏贝叶斯学习（SBL）模型进行建模，并通过VBEM方法求解后验分布近似值，从而构建SBL-VBEM模型。由于SBL-VBEM模型的重构结果仍然受字典矩阵的相关性影响，因此通过减少字典列之间的相互一致性来改善重构结果。首先，通过S形函数的拓扑结构获得收缩因子；然后，在获取一致受限字典的每次迭代中，利用收缩因子缩小字典矩阵中最大非对角项的邻域间隔；最后，将获取的一致受限字典作为SBL-VBEM模型的输入，获得更有效的重构织物图像。对CCD-VBEM模型在阿里云天池数据集上进行验证，验证结果表明，在不同采样率（0.20～0.40）下，CCD-VBEM模型对织物图像的重构均获得最优性能。

关键词：织物图像；重构；一致受限字典；变分贝叶斯期望最大化；收缩因子

中图分类号：TP181

文献标志码：A

文章编号：1009-265X（2024）09-0117-10

收稿日期：2023-12-13

网络出版日期：2024-03-20

基金项目：国家自然科学基金项目（U1709219，61601410）；浙江省科技厅重点研发计划项目（2021C01047，2022C01079）；产业技术基础公共服务平台项目（2021-0174-1-1）

作者简介：陈影柔（1999—），女，贵州黔西南州人，硕士研究生，主要从事计算机视觉方面的研究。

通信作者：吕文涛，E-mail：alvinlwt@zstu.edu.cn

随着数字化转型的发展，纺织业逐步数字化、智能化和自动化，人工分拣、人工检查被优秀的计算机视觉算法和精密的仪器所替代，实现高精度、高效率、低成本和低损耗的生产^［1-2］。在大数据时代下，图像数据日益增多，然而硬件对图像数据处理能力终究受限，因此，为了提高智能纺织业的核心竞争力，需要大力提高计算机视觉算法软实力。在智能纺织工业生产中，织物图像的采集、传输、存储、检测等环节都是不可或缺的，而传输作为关键的一环影响着织物图像数据的处理能力。然而图像在传输过程中总存在压缩损失。织物图像本身的规则纹理因失真而被破坏^［3］，会导致织物缺陷检测^［4］、织物纹理表征^［5］、织物密度检测^［6］等其他算法的性能受限。为了降低织物图像在传输过程中受到压缩损失，稀疏表示和稀疏重构可以很好地解决了这一问题。

稀疏表示是在织物图像的传输过程中对图像进行压缩，稀疏重构则是对压缩的数据进行图像的恢复。稀疏表示通过测量矩阵将原始数据稀疏化，原始数据不仅可以简洁地表达，还提取出有效的特征信息。稀疏表示的前提是图像可以被精确重构^［7］。稀疏重构算法作为稀疏表示的逆问题^［8］，在计算机视觉领域获得许多成果，例如压缩感知^［9］、图像处理^［10］、图像去噪^［11］、图像重构^［12］等。稀疏重构通过测量矩阵将稀疏信号投影到低维空间进行求解，使得原始信号在不丢失信息的前提下大概率地被重构^［13］。稀疏重构算法最终的重构效果取决于产生优化过程的重构模型。根据稀疏表示理论，通常将稀疏表示模型表示为：

y=Dω（1）

式中：y∈R^M×1表示观测信号，D∈R^M×N表示测量矩阵（也称为字典），ω∈R^N×1表示待估计的稀疏解向量，M与N表示维度。

由于稀疏表示的建模简单，稀疏重构模型的优化方向可以分为以下两种。一种是通过优化字典D来提高重构性能^［14-17］。Jiang等^［14］提出了一种用于人脸和对象类别识别的K奇异值分解（K-Singular value decomposition，K-SVD）字典学习方法，即引入新的标签一致性约束，并将其与重构误差相结合，形成统一的目标函数，从而获得良好的重构效果。Jing等^［15］提出了一种卷积匹配追踪双字典算法来检测图案化织物图像中的缺陷。Zhan等^［16］提出了一种区分共享字典学习模型，通过基于低秩约束和相似性约束来优化字典，该模型有效地提取了特定类图像的特征。这些方法侧重于词典学习的优化设计，然而大多数模型没有很好地考虑字典矩阵列之间的互相关性；当互相关性较强时，这可能让自然图像的重构性能提升总是存在一个上限。

另一种则是通过求解最优稀疏信号ω来精确重构图像^［18-20］，求解的方法可以大致分为3种：贝叶斯、贪婪迭代以及最优逼近。稀疏贝叶斯学习（Sparse Bayesian learning，SBL）^［21］作为贝叶斯模型的一种新兴技术，具有高稀疏性、强鲁棒性以及逻辑的严谨性等特点。SBL通过求解稀疏解向量的后验概率，可以获得较高的重构精度。Wipf等^［22］应用SBL模型在单个测量向量模型中重构稀疏信号，其缺点在于重构过程收敛较慢导致计算效率低。针对此问题，Zhang等^［23］提出了块稀疏贝叶斯学习（Block sparse Bayesian learning，BSBL）方法来快速恢复稀疏系数，该方法主要将信号视为块结构，从而将信号划分为多个块进行重构，达到提高重构效率的目的。Serra等^［24］将K-SVD字典学习式引入SBL模型，以抑制具有简单背景的光学图像中的噪声。然而，这些基于SBL的方法直接应用于真实场景时，各方面的重构性能受到一定的限制。主要有以下原因：a）这些算法需要真正等效的稀疏字典作为感测矩阵，并且这些等效字典在重构前就需要是已知的；b）由于字典是为特定目标精心设计的，很难扩展到其他对象，降低了算法的鲁棒性；c）在现实应用场景中，稀疏图像往往具有复杂的结构，SBL方法在后验估计时，它的计算复杂度随着问题的大小而显著增加。Fox等^［25］通过EM算法与变分贝叶斯理论相结合设计了一种广义EM算法，即变分贝叶斯期望最大化（Variational Bayesian expectation maximization，VBEM），利用VBEN算法对模型参数进行简化估计，从而得到模型后验分布信息的近似估计，提高算法模型的运算效率及鲁棒性。近几年来，学者们基于VBEM算法衍生出许多重构模型^［26-27］，在图形重构上均取得一定的成果。毛兆华等^［3］提出了基于字典学习的机织物图像的重构算法，该算法通过分解机织物纹理信号的线性表达来学习字典，字典的线性组合可以在一定的约束下对机织物图像进行最优的重构。

本文提出了一个基于VBEM的一致受限字典织物图像重构（CCD-VBEM）模型，采用多层先验模型建模和VBEM方法求解后验分布近似值，以构建SBL-VBEM模型来降低计算复杂度。除此之外，为提高SBL-VBEM模型对织物图像的重构质量，本文在SBL-VBEM模型的基础上加入一致受限字典优化式，以构建CCD-VBEM模型。一致受限字典优化式提供了一种新的S形函数拓扑结构以获得收缩因子，并在字典的每次迭代中使用收缩因子缩小字典矩阵中最大非对角项的邻域间隔，以此来快速获得字典矩阵的列之间的较低互相关，这有利于CCD-VBEM模型重构更好的稀疏信号。CCD-VBEM模型进一步提高了织物图像的重构精度，减少了织物图像在传输过程中的压缩失真。本文在公共织物图像数据集进行实验，以验证本文提出方法的有效性。

1 稀疏贝叶斯（SBL）的理论基础

SBL模型建立的本质是为了解决稀疏信号恢复（Sparse signal recovery，SSR）问题和相关的压缩感知问题。单个测量向量的情况下，SSR问题包括从M≤N个有噪声的测量向量y∈R^M×1中恢复稀疏信号ω∈R^N×1［28］。SBL的数学模型可以表示为：

y=Dω+ζ（2）

式中：D∈R^M×N是已知的观测矩阵，ζ∈R^M×1是观测噪声。

在SBL框架中，假定ζ服从均值为0、方差为的高斯分布，即ζ～N（0，σ²），令θ=σ^-2，则测量向量y的高斯似然函数的表达式可以写成：

类似地，本文假设ω的项ω是独立分布的，并假设ω服从高斯分布，且均值为0，方差为λ^-1，ω的先验分布函数的表达式可以写成：

式中：λ {λ}是控制信号ω稀疏性的非负超参数，Ω diag（<λ>，<λ>，···，<λ>），根据贝叶斯理论，SBL模型的后验概率分布可以表示为：

由于p（y|ω;θ）、p（ω|λ）均服从高斯分布，因此p（ω;λ，θ|y）也服从高斯分布，且均值μ和协方差矩阵∑可以表示为：

2 基于VBEM的一致受限字典重构模型（CCD-VBEM）

2.1 多层先验模型

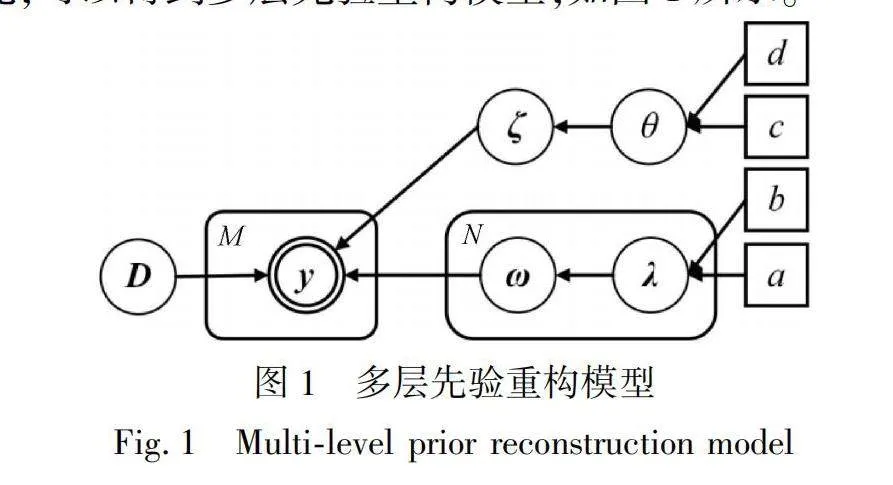
考虑织物图像的真实应用场景，结合变分推断的思想，在SBL的框架上构建多层先验的重构模型，式（2）可以改写为：

y=Dω（λ（a，b））+ζ（θ（c，d））（8）

式中：λ为精度参数，a、b分别为形状参数和尺度参数。形状参数a是对上层先验分布的形状表达进行约束，尺度参数b则是对上层先验分布的幅度变化进行约束。同理，ζ表示确定性噪声模型，c、d分别为控制噪声模型精度参数θ的形状参数和尺度参数。由此，可以得到多层先验重构模型，如图1所示。

在此多层先验重构模型中，指定超参数λ服从Gamma分布，即：

p（λ）=∏Ni=1p（λ;a，b）=∏Ni=1Gamma（λ|a，b）

=∏Ni=1b^aΓ（a）λ^a-1exp（-bλ）（9）

其中Γ（x）=∫^∞t^x-1e^-tdt为Gamma函数。同理，为了学习精度参数θ，本文假设θ也服从Gamma分布，即

p（θ）=p（θ;c，d）=Gamma（θ|c，d）

=d^cΓ（c）θ^c-1exp（-dθ）（10）

根据贝叶斯理论和变分贝叶斯推断理论，图1中重构模型的后验概率分布可以表示为：

p（ω;λ，θ|y）=p（y|ω;θ）p（ω|λ）p（λ）p（θ）p（y;λ，θ）（11）

因此，p（y;λ，θ）的边际似然函数可以表示为：

p（y;λ，θ）=∫p（y|ω;θ）p（ω|λ）p（λ）p（θ）dωdλdθ（12）

2.2 变分贝叶斯期望最大化（VBEM）推理

由于式（12）的求解非常困难，所以根据变分推断思想，利用VBEM算法对模型的后验概率分布进行估计，模型的VBEM估计表达式为：

p（ω;λ，θ|y）∝Q（ω，λ，θ）=Q（ω）Q（λ）Q（θ）（13）

VBEM算法的目标是最大化Q（ω）、Q（λ）以及Q（λ）。VBEM推理分为两步：VBE-Step和VBM-Step。与EM算法相似，VBEM在对后验分布信息进行估计时，仍然需要采用交替迭代的策略。通过VBE-Step更新Q（ω），再将新的Q（ω）作为VBM-Step的输入对Q（λ）和Q（θ）进行更新。VBE-Step和VBM-Step的不断迭代，直到达到收敛条件停止更新输出最终结果。在织物图像的实际应用中，VBEM算法比EM算法大大的加快了计算速率，更加适用于工业场景。VBE-Step和VBM-Step的具体原理如下。

2.2.1 VBE-Step

更新Q（ω）。忽略与ω无关的项，则Q（ω）的近似后验分布可由式（14）计算（<·>表示求期望）：

lnQ（ω）∝＜lnp（y|ω;θ）p（ω|λ）＞

∝＜-θ2y-Dω²-12ω^TΩω＞

∝＜-θ2（y^Ty-2y^TDω+ω^TD^TDω）

-12ω^TΩω＞

∝-12ω^T（＜θ＞D^TD+＜Ω＞）ω

-＜θ＞y^TDω（14）

显然，Q（ω）遵循高斯分布，其均值μ和协方差∑分别表示为：

ω=μ=<θ>∑D^Ty（15）

∑=（<θ>D^TD+<Ω>）^-1（16）

2.2.2 VBM-Step

更新Q（λ）。忽略与λ无关的项，则Q（λ）的近似后验分布可由式（17）计算（<·>表示求期望）：

lnQ（λ）∝＜lnp（ω|λ）p（λ）>

∝∑Ni=1（（a-12）lnλ-（<ω²>2+b）λ）

∝∑Ni=1（（a^-1）lnλ-b^λ）（17）

式中：<ω²>=μ+∑；μ表示的第i个元素；∑表示对角矩阵中的第i个元素。令a^=a+12，b^=<ω²>2+b。由式（17）可以得出：

Q（λ）=∏Ni=1Gamma（λ;a^，b^）（18）

<λ>=a^b^（19）

更新Q（θ）。忽略与θ无关的项，则Q（θ）的近似后验分布可由式（20）计算（<·>表示求期望）：

lnQ（θ）∝<lnp（y|ω;θ）p（θ）>

∝（c-1+M2）lnθ-（12<y-Dω²>+d）θ

∝（c^-1）lnθ-d^θ（20）

式中：<y-Dω²>=y-Dμ²+tr（D^T∑D）。令c^=c+M2，d^=12<y-Dω²>+d，由式（20）可以得出：

Q（θ）=Gamma（θ;c^，d^）（21）

<θ>=c^d^（22）

根据式（15）—（16）、式（19）和式（22）的迭代计算可以估计出期望最大的稀疏信号ω。

2.3 一致受限字典

为了让织物图像的重构性能获得各方面的提升，本文在SBL-VBEM模型上融入了对字典的优化，使得CCD-VBEM模型的重构精度更加精确。CCD-VBEM重构模型如图2所示。

通常，相互一致性用于衡量字典列之间的相关性。在式（15）—（16）中，字典D的列之间有较低的相互一致性可以获得更好的重构结果。因此，有必要减小字典D每一列之间的线性相关性，从而获得更好的解决方案。格拉姆矩阵是求解线性相关问题的一个较好解决方案，矩阵的每一个元素实际上是在计算两两特征之间的相关性。本文考虑使用格拉姆矩阵将字典D的每一列两两关联，并提出新的规则约束格拉姆矩阵，以减小字典D的相互一致性。格拉姆矩阵可以表示为G=D^TD，则字典D的相互一致性可以表示为：

Ψ{D}=max1≤i，j≤N，i≠j|d|（23）

式中：d=<d，d>。理论上，相互一致性有一个下限。对于大小为M×N（M<N）的全秩矩阵，相互一致性由下式作为下限：

Ψ≥（M-NN（M-1））¹²（24）

本文的优化目标是使字典D的相互一致性在每次迭代中接近下限^［28-29］。多次迭代后可以获得理想的字典矩阵。文献［29-30］中提到每次迭代中仅更新最大非对角项，可以大大地加快计算效率。在本文提出的方法中，基于S形函数的拓扑结构提供了一个新的收缩因子ρ（0<ρ<1），达到快速优化的目的，其表达式如下：

ρ=γ11+e^-kΨ{D}+ν（25）

式中：γ和k用于控制收敛速度。γ是一个常数，可以通过实验确定。ν表示校正偏移量。注意，D的初始化使用随机高斯矩阵获得。

3 实验

为了评估CCD-VBEM算法的重构性能，本文将CCD-VBEM算法在阿里云天池数据集^［31］和浙江大学所提供的ZJU-Leaper数据集^［32］上进行实验，与经典的SBL-EM^［22］、SBL-VBEM^［25］、KSVD-SBL^［24］以及BSBL^［23］等4种不同模型进行实验对比，采用图像质量相关的评价指标来衡量不同方法的性能。

3.1 CCD-VBEM算法流程

算法1：CCD-VBEM

输 入：样本y，字典D^（0），超参数Ω^（0）、θ^（0）、a、b、c、d，阈值ε、ε，参数γ、k、ν；

初始化：t、t=0，maxIter、maxIter=5000；

步骤 1：计算格拉姆矩阵G^（t）：

G^（t）=D^（t）TD^（t）；

步骤 2：利用式（23）找到最大非对角项（d）；

步骤 3：利用式（25）优化收缩因子ρ；

步骤 4：更新最大非对角项：

d≥ρ×（d）；

步骤 5：使用奇异值分解（SVD）算法降低G^（t）的秩：

［U，S，V］=SVD（G^（t）），S（M+1：end，M+1：end）=0，G^（t+1）=U·S·V^T；

步骤 6：对G^（t+1）的列进行归一化，获得新的字典D^（t+1）：

D^（t+1）T·D^（t+1）=G^（t+1）；

步骤 7：利用式（23）计算字典D^（t+1）的相关一致性，并通过|Ψ（D^（t））-Ψ（D^（t+1））|<ε和t>maxIter判断是否达到收敛条件，如果到达收敛条件，令D=D^（t+1），且继续步骤8；反之回到步4EkkmzDWt0NFmW//Ixj49Q==骤1，且令t=t+1；

步骤 8：利用式（15）和（16）估计均值μ^（t）和协方差∑^（t）；

步骤 9：利用式（19）和（22）估计超参数<λ>^（t）、<θ>^（t）；

步骤10：通过μ^（t）-μ^（t-1）2μ^（t）2<ε和t>maxIter判断是否达到收敛条件，如果到达收敛条件，令ω=μ^（t），结束算法；反之回到步骤8，且令t=t+1；

输出：利用稀疏信号ω输出重构图像。

3.2 算法参数设定

在整个实验中，本文为CCD-VBEM算法设置了必要的参数值。设置的参数值使得算法迭代过程无过拟合现象，参数a、b、c、d、γ、k和ν的初始值分别设置为1×10^-6、1、1×10^-6、1、1.8、0.74和20。在算法1中的阈值参数ε和ε分别设置为1×10^-6和1×10^-5。另外，字典矩阵D采用高斯随机矩阵初始化。

3.3 实验环境

本文实验验证程序的运行环境均满足在Matlab 2016a中编写，计算机配置为2.4 GiHz Intel Xeon Silver的CPU和64 Gi RAM的DELL Workstation 7920T以及 Windows 10操作系统中运行。

4 结果与分析

为验证CCD-VBEM算法对织物图像重构的有效性，本文设计了包括KSVD-SBL、SBL-EM、SBL-VBEM以及BSBL方法在内的多组对照实验，实验通过图像质量评价指标峰值信噪比（Peak signal-to-noise ratio，PSNR）和结构相似度（Structural similarity，SSIM）进行定量的分析和比较。每种方法采用不同采样率κ对图像进行稀疏化，以验证算法的性能。采用不同采样率κ进行多组实验。κ的取值范围为0.20～0.40，步长为0.05。为保证所有方法获得最佳的结果，所有的比较方法都是根据文献提出的最优参数值来设置。KSVD-SBL方法是通过对标准图像的特征学习获得字典，BSBL方法使用原始的伯努利字典矩阵，并设置划分块数目为64。

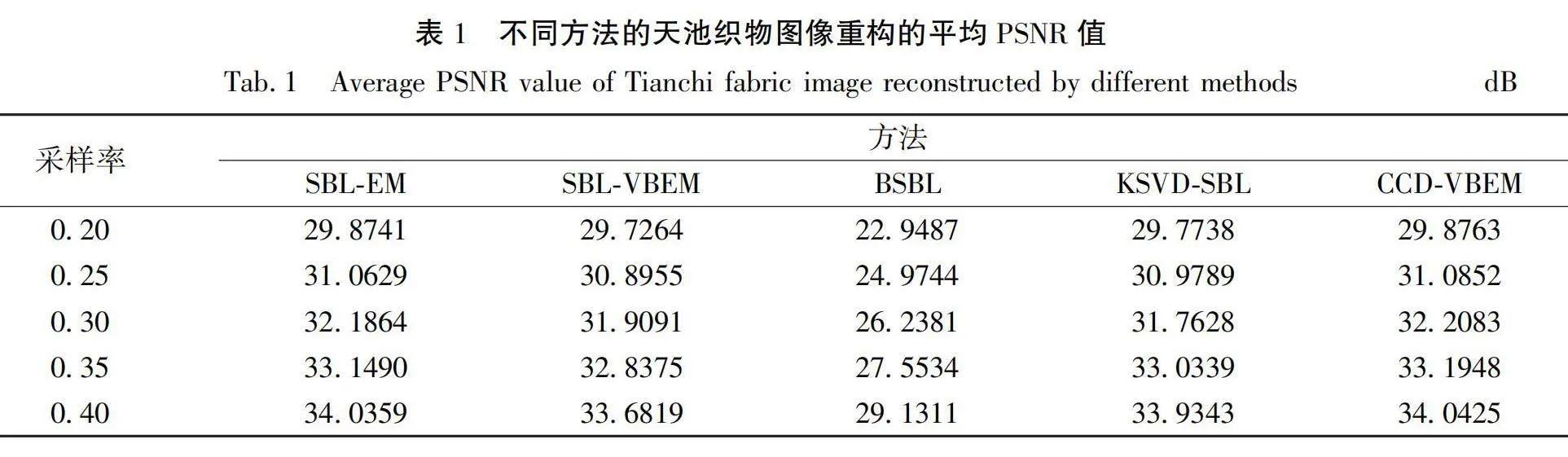
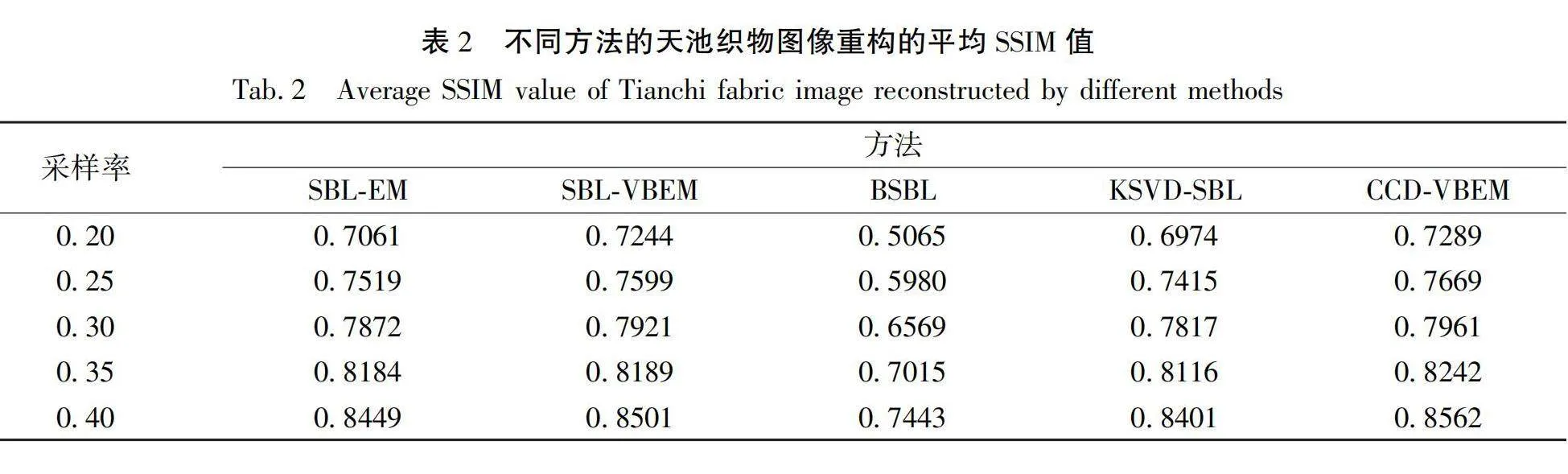
第一组实验图像来自阿里云的天池数据集，图像对象是纺织布匹，图像为256×256像素。随机挑选3张织物图像进行重构效果展示。图3分别展示了不同方法的重构图像（κ=0.30）。从图3中可以看出，CCD-VBEM算法、KSVD-SBL算法和SBL-EM算法重构出来的织物图像与原图最为近似，而BSBL方法的重构效果相对较差。造成这样结果的原因有两个：一是BSBL使用块结构进行了更新，以牺牲重构精度的方式提高了重构效率；二是织物图像呈现出更加规则的纹理，而分块更新破坏了这一规则。除此之外，为了获得更为详细的重构性能数据，从织物数据集中随机选取50张图像作为样本用不同方法进行重构，重构的PSNR和SSIM均值结果如表1和表2所示。

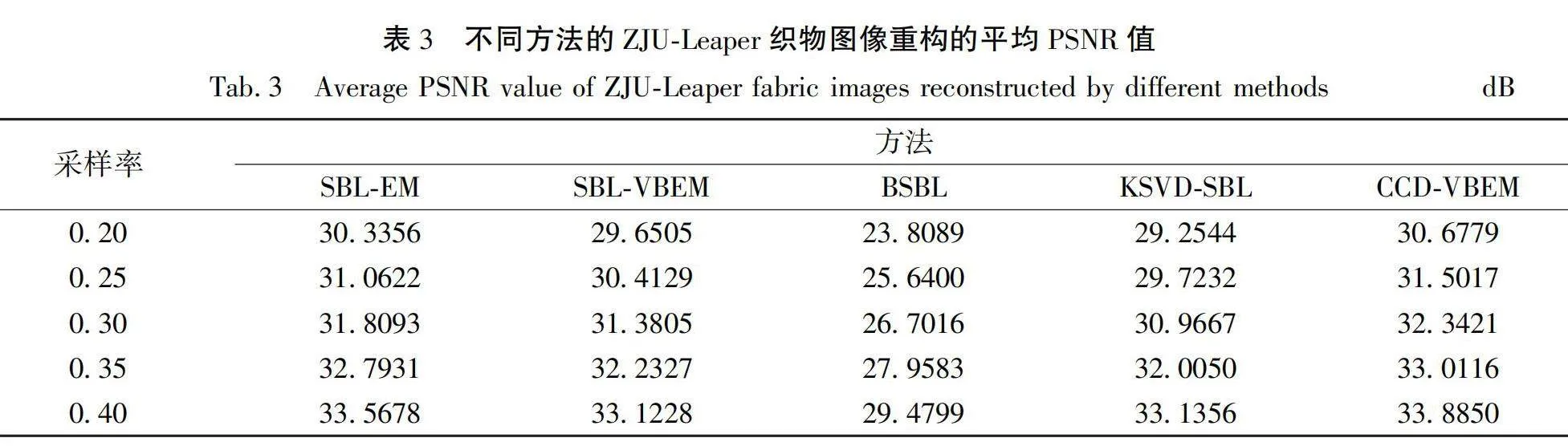
从表1和表2可以看出，CCD-VBEM方法优于所有对比方法，在不同的采样率内均获得最高的PSNR和SSIM。采样率为0.40时，CCD-VBEM方法的PSNR为34.0425 dB；SBL-EM方法的PSNR为34.0359 dB，仅次于CCD-VBEM；而PSNR最低的仍然是BSBL方法，其值为29.1311 dB，相较于CCD-VBEM方法降低了4.9114 dB。相对于SBL-VBEM算法而言，CCD-VBEM算法的PSNR值和SSIM值都得到了一定的提升，这得益于一致受限字典对SBL-VBEM模型的优化，进一步证明了本文提出的方法的有效性。

第二组实验图像是由浙江大学提供的ZJU-Leaper数据集，图像类型共有19种，图像为512×512像素。随机挑选3张织物图像进行重构效果展示（κ=0.30），分别是花卉印花1、花卉印花2、红格子3种类型（对应图像从上向下排序），如图4所示。

从图4可以看出CCD-VBEM算法和SBL-EM算法的重构在纹理和印花上做到与原图最优的近似，SBL-VBEM算法和SBL-EM算法在3张织物图像上也展现了良好的重构效果。KSVD-SBL算法对花卉印花1图像的纹理重构不够完整，但对花卉印花2和红格子图像上的重构效果不弱于SBL-VBEM算法和SBL-EM算法。而BSBL的重构造成了严重的失真，几乎无法辨认原图像的纹理和印花。

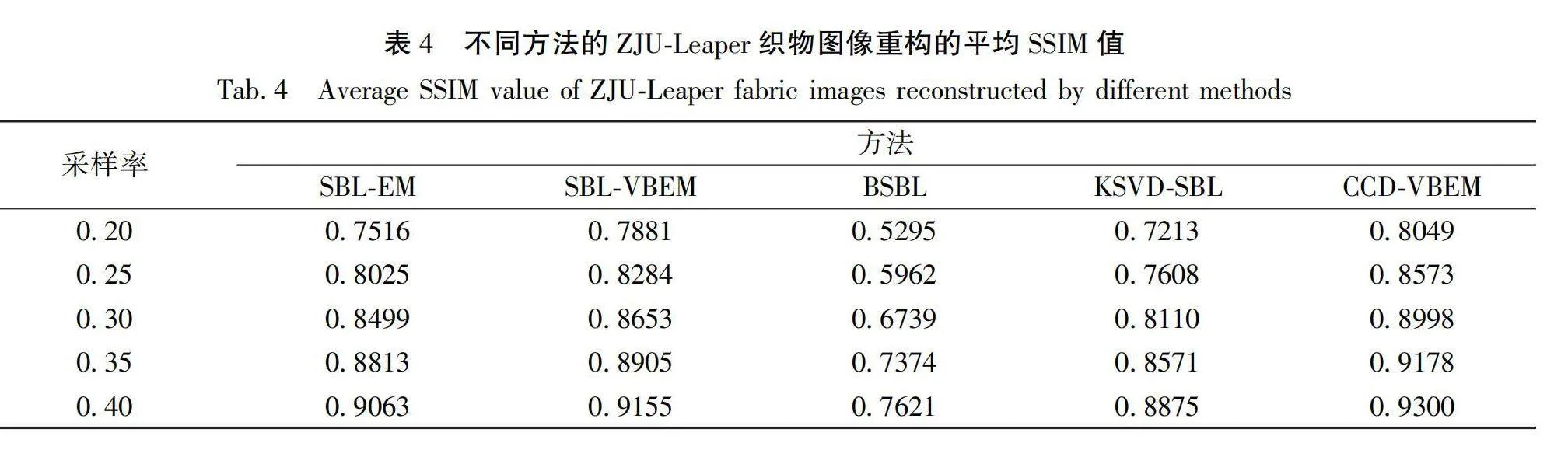
为了增强算法的鲁棒性，从ZJU-Leaper数据集中随机选取50张图像作为样本进行重构，重构的PSNR和SSIM均值结果如表3和表4所示。从表3和表4可以看出，CCD-VBEM方法在ZJU-Leaper数据集上获得了最佳重构性能。采样率为0.40时，CCD-VBEM方法的PSNR为33.8850 dB。同样地，SBL-EM方法和SBL-VBEM方法的峰值信噪比仅次于CCD-VBEM方法，说明CCD-VBEM方法的重构误差较小，尽可能地保证不失真。而BSBL方法的PSNR仅为29.4799 dB不适用于织物图像的重构，无论是峰值信噪比还是结构相似度都没有达到理想的值。CCD-VBEM方法将优化后的字典集成在VBEM模型上，进一步提升了图像重构的精度，减小误差，同时提升了织物图像重构后的结构相似性，尽可能地保证织物纹理的复原。

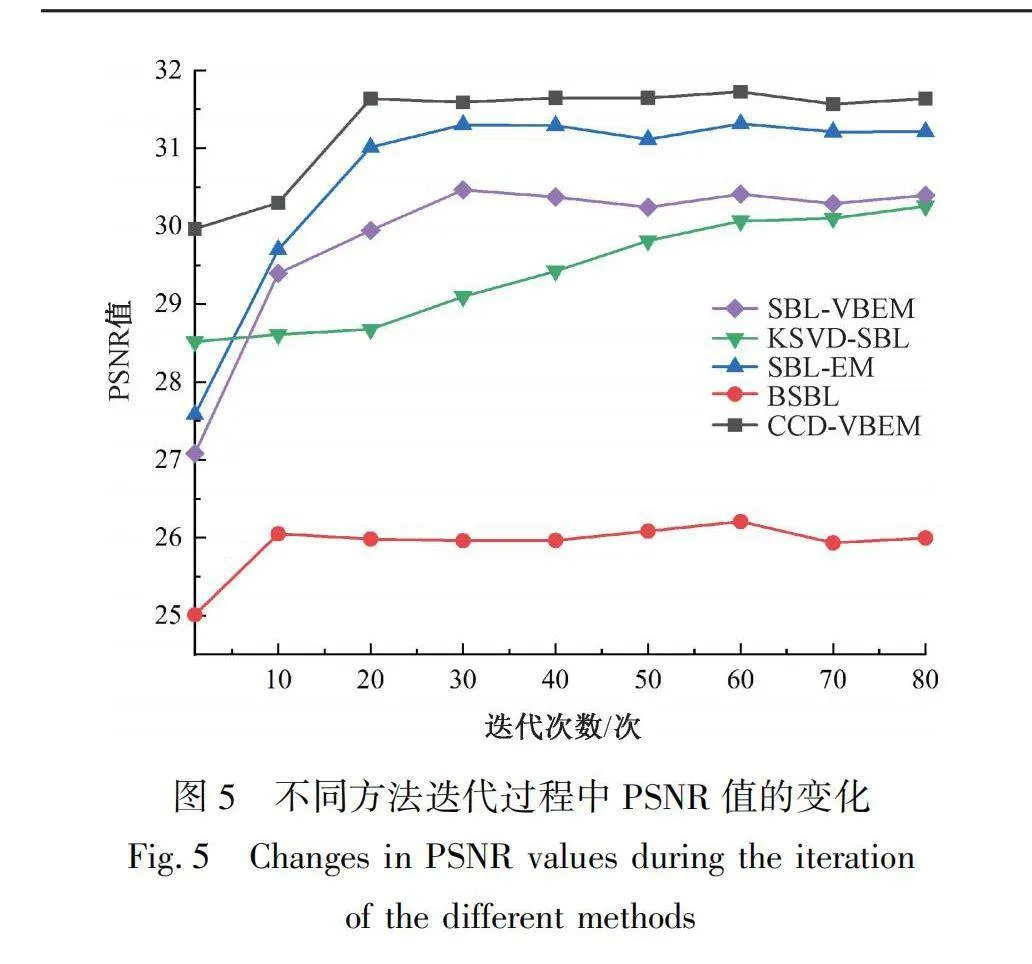
此外，本文还进行了不同方法之间的重构效率对比，如表5所示。在不同采样率下，BSBL方法获得最快重构速度，这归功于它的分块机制。而本文提出的CDD-VBEM方法仅次于BSBL方法，且在高采样率的条件下，重构时间大大缩短，获得了几乎接近BSBL方法的重构效率。为了更详细地分析算法优势，图5展示了织物图像重构算法在迭代过程中PSNR值的变化。从图5可知，在对照实验中，BSBL收敛最快，迭代约10次完成收敛，但是重构精度受限。而本文提出的CCD-VBEM方法约20次完成收敛，且获得了最优重构精度。虽然CCD-VBEM方法的模型相较于SBL-VBEM方法的模型多了字典优化模块，但是CCD-VBEM方法比SBL-VBEM方法重构效率高，这是因为CCD-VBEM方法引入的一致受限字典加快了模型的收敛，使得模型提高重构精度的同时保持了重构效率。

5 结论

本文提出了一种基于VBEM的一致受限字典织物图像重构模型CCD-VBEM。CCD-VBEM模型采用多层先验模型建模，并用VBEM方法求解后验分布近似值，以构建SBL-VBEM模型来降低计算复杂度。除此之外，本文提出了一种新的S形函数拓扑结构，该结构计算获得收缩因子。CCD-VBEM模型通过收缩因子优化SBL-VBEM模型中字典的相互一致性，不仅提升了传统的SBL-VBEM模型的重构精度，还进一步加快了重构的收敛速度。阿里云天池数据集中的织物图像证明了本文所提方法的有效性。

然而，本文所提方法在重构效率仍受到计算复杂度的限制。为了进一步降低EM算法中E步的计算复杂度，需要从广义近似消息传递研究入手，进一步提高重构精度以及重构效率。

参考文献：

［1］靳文哲， 吕文涛， 郭庆， 等. 基于改进3E-LDA的织物图像分类算法［J］. 现代纺织技术， 2024， 32（6）：89-96.

JIN Wenzhe， LÜ Wentao， GUO Qing， et al. Fabric image classification algorithm based on improved 3E-LDA［J］. Advanced Textile Technology， 2024， 32（6）：89-96.

［2］吕文涛， 林琪琪， 钟佳莹， 等. 面向织物疵点检测的图像处理技术研究进展［J］. 纺织学报， 2021， 42（11）： 197-206.

LÜ Wentao， LIN Qiqi， ZHONG Jiaying， et al. Research progress of image processing technology for fabric defect detection［J］. Journal of Textile Research， 2021， 42（11）： 197-206.

［3］毛兆华， 万贤福， 汪军， 等.基于字典学习的机织物图像重构［J］.东华大学学报（自然科学版），2016，42（1）：35-39.

MAO Zhaohua， WAN Xianfu， WANG Jun， et al. Woven fabric image reconstruction based on dictionary learning［J］.Journal of Donghua University （Natural Science）， 2016，42 （1）： 35-39.

［4］付晗， 胡峰， 龚杰， 等. 面向织物疵点检测的缺陷重构方法 ［J］. 纺织学报， 2023， 4pd2sve16KpvboITqbxVvu/pYWttICl+Qg6mK/Z+LxmE=4（7）： 103-109.

FU Han， HU Feng， GONG Jie， et al. Defect reconstruction algorithm for fabric fault detection ［J］. Journal of Textile Research， 2023， 44（7）： 103-109.

［5］占竹， 王凯， 李立轻， 等. 基于通用学习字典的机织物纹理表征［J］. 棉纺织技术， 2021， 49（1）： 34-39.

ZHAN Zhu， WANG Kai， LI Liqing， et al. Woven Fabric Texture Characterization Based on General Dictionary ［J］. Cotton Textile Technology， 2021， 49 （1）： 34-39.

［6］彭然， 胡立文， 邓中民. 基于Radon变换和能量曲线的机织物密度检测［J］. 棉纺织技术， 2021， 49（4）：16-20.

PENG Ran， HU Liwen， DENG Zhongmin. Detection of Woven Fabric Density Based on Radon Transform and Energy Curve ［J］. Cotton Textile Technology， 2021，49 （4）： 16-20.

［7］曾艳， 王萌， 邢婷婷， 等. 一种改进的压缩感知彩色图像重构框架［J］. 计算机应用与软件， 2023， 40（9）： 248-252.

ZENG Yan， WANG Meng， XING Tingting， et al. An improved framework for color image reconstruction based on［J］. Computer Applications and Software， 2023，40 （9）： 248-252.

［8］赵东波， 李辉. 基于改进平滑L0算法的图像重构［J］.信息技术， 2023， 47（9）： 103-107.

ZHAO Dongbo， LI Hui. lmage reconstruction based on improved Smoothing L0 algorithm ［J］. Information Technology， 2023， 47（9）： 103-107.

［9］BABACAN S D， MOLINA R， KATSAGGELOS A K. Bayesian compressive sensing using Laplace priors［J］. IEEE Transactions on Image Processing Society， 2010， 19（1）： 53-63.

［10］ZHANG Y， QI X， JIANG Y， et al. Image Reconstruction for low-oversampled staggered SAR based on Sparsity Bayesian learning in the presence of a nonlinear PRI variation strategy［J］. IEEE Transactions on Geoscience and Remote Sensing， 2022， 60： 1-24.

［11］张睿颖. 稀疏表示图像去噪算法研究及在海浪反演中的应用［D］. 大连： 大连海洋大学， 2023： 8-53.

ZHANG Ruiying. Research on Sparse Representation based Image Denoising Algorithm and Its Application in Wave Inversion ［D］. Dalian： Dalian Ocean University， 2023：8-53.

［12］杨孟宇. 基于压缩感知的高光谱图像重构算法研究［D］. 哈尔滨： 哈尔滨理工大学， 2023： 9-64.

YANG Mengyu. Research on Hyperspectral Image Reconstruction Algorithm Based on Compressed Sensing ［D］. Harbin： Harbin University of Science and Technology， 2023： 9-64.

［13］毛璐. 基于稀疏表示的逆问题研究［D］. 西安： 西安石油大学， 2023： 6-54.

MAO Lu. Research on Inverse Problem Based on Sparse Representation ［D］. Xi'an： Xi'an Shiyou University， 2023： 6-54.

［14］JIANG Z， LIN Z， DAVIS L S. Label consistent K-SVD： Learning a discriminative dictionary for recognition［J］. IEEE transactions on pattern analysis and machine intelligence， 2013， 35（11）： 2651-2664.

［15］JING J， FAN X， LL P. Patterned fabric defect detection via convolutional matching pursuit dual-dictionary［J］. Optical Engineering， 2016， 55（5）： 053109.

［16］ZHAN Z， LI L， CHEN X， et al. Discriminative-shared dictionary learning for class-specific fabric texture characterization［J］. Textile Research Journal， 2020， 90（21/22）： 2478-2491.

［17］LÜ W， ZHOU D， WANG C， et al. A novel discriminative dictionary learning method for image classification［J］. IEICE Transactions on Fundamentals of Electronics， Communications and Computer Sciences， 2023， 106（6）： 932-937.

［18］AL-SHOUKAIRI M， SCHNITER P， RAO B D. A GAMP-based low complexity sparse Bayesian learning algorithm［J］. IEEE Transactions on Signal Processing， 2018， 66（2）： 294-308.

［19］李德高， 程涛， 许聪， 等. 基于后验信息的压缩感知图像重构方法［J］. 广西科技大学学报， 2023， 34（4）： 12-16.

LI Degao， CHENG Tao， XU Cong， et al. Compressed sensing image reconstruction method based on posterior information ［J］. Journal of Guangxi University of Science and Technology， 2023，34 （4）： 12-16.

［20］DUAN H， YANG L， FANG J， et al. Fast inverse-free sparse Bayesian learning via relaxed evidence lower bound maximization［J］. IEEE Signal Processing Letters， 2017， 24（6）： 774-778.

［21］DONG J， LÜ W， ZHOU D， et al. Variational Bayesian and generalized approximate message passing-based Sparse Bayesian learning model for image reconstruction［J］. IEEE Signal Processing Letters， 2022， 29： 2328-2332.

［22］WIPF D P， RAO B D. Sparse Bayesian learning for basis selection［J］. IEEE Transactions on Signal processing， 2004， 52（8）： 2153-2164.

［23］ZHANG Z， RAO B D. Recovery of block sparse signals using the framework of block sparse Bayesian learning［C］//IEEE International Conference on Acoustics， Speech and Signal Processing （ICASSP）. IEEE， 2012： 3345-3348.

［24］SERRA J G， TESTA M， MOLINA R， et al. Bayesian K-SVD using fast variational inference［J］. IEEE Transactions on Image Processing， 2017， 26（7）： 3344-3359.

［25］FOX C W， ROBERTS S J. A tutorial on variational Bayesian inference［J］. Artificial intelligence review， 2012， 38： 85-95.

［26］苏挺超， 沈映珊. 基于分层贝叶斯模型的图像修复方法［J］. 计算机应用与软件， 2023， 40（10）： 261-267.

SU Tingchao， SHEN Yingshan. Image inpainting method based on hierarchical bayesian model［J］. Computer Applications and Software， 2023，40 （10）： 261-267.

［27］甘宜超. 基于贝叶斯理论的雷达成像技术研究［D］. 西安： 西安电子科技大学， 2020： 14-73.

GAN Yichao. Research on Radar Imaging Technology Based on Bayesian Theory ［D］. Xi'an： Xidian University， 2020： 14-73.

［28］LÜ W， WANG J， YU W， et al. Improvement of semi-random measurement matrix for compressed sensing［J］. IEICE Transactions on Fundamentals of Electronics， Communications and Computer Sciences， 2014， 97（6）： 1426-1429.

［29］ELAD M. Optimized projections for compressed sensing［J］. IEEE Transactions on Signal Processing， 2007， 55（12）： 5695-5702.

［30］DUARTE-CARVAJALINO J M， SAPIRO G. Learning to sense sparse signals： Simultaneous sensing matrix and sparsifying dictionary optimization［J］. IEEE Transactions on Image Processing， 2009， 18（7）： 1395-1408.

［31］TIANCHI A. Smart diagnosis of cloth flaw dataset［EB/OL］. （2020-10-21）［2021-11-05］. https：//tianchi.aliyun.com/dataset/dataDetail？dataId=79336.

［32］ZHANG C， FENG S， WANG X， et al. Zju-leaper： A benchmark dataset for fabric defect detection and a comparative study［J］. IEEE Transactions on Artificial Intelligence， 2020， 1（3）： 219-232.

A consistent constrained dictionary model based on VBEM for fabric image reconstruction

CHEN Yingrou¹， LÜ Wentao¹， YU Runze²， GUO Qing³， XU Yuzhen³

（1.Key Laboratory of Intelligent Textile and Flexible Interconnection of Zhejiang Province，Zhejiang Sci-Tech University， Hangzhou 310018， China; 2.China Mobile Group Design Institute Co.， Ltd.， Zhejiang Branch， Hangzhou 310012， China; 3.Zhejiang Technical Innovation Service Center， Hangzhou 310007， China）

Abstract： With the culmination of digital transformation， the textile industry， as an important component of the manufacturing sector， is gradually moving towards the field of intelligent manufacturing. By introducing advanced digital technologies and automation systems， the textile industry can achieve high efficiency and precision in the production process. The application of automation equipment and robots can reduce human errors and labor costs while improving production efficiency. With continuous technological advancements and changing market demands， the textile industry is facing numerous challenges and opportunities. The advent of big data has led to a significant increase in data volume， which poses a significant burden on intelligent manufacturing. Additionally， the increased volume of image data in particular can lead to compression distortion during the transmission process. To address this， compressing images using sparse representation technology can avoid wastage of resources during transmission. Sparse reconstruction， as the inverse problem of sparse representation， is crucial for accurately restoring the sparse-represented image data without losing the original information.

To enhance the core competitiveness of the textile industry， this paper proposed a VBEM （variational Bayesian expectation maximization）-based consistent constrained dictionary （CCD-VBEM） model for fabric image reconstruction. It addressed the problem of decreased reconstruction performance caused by strong inter-column consistency in traditional sparse Bayesian algorithms. Considering the real-world application scenarios of fabric images， a multi-layer prior sparse Bayesian learning （SBL） model was adopted for modeling， and the VBEM method was used to approximate the posterior distribution. This resulted in the construction of the SBL-VBEM model. However， the reconstruction results of the SBL-VBEM model are still affected by the coherence of the dictionary matrix. To improve the reconstruction results， this paper reduced the inter-column consistency of the dictionary matrix.

To achieve this goal， the paper first obtained a shrinkage factor using the topological structure of the sigmoid function. With the shrinkage factor， the neighborhood interval of the largest off-diagonal entry in the dictionary matrix can be reduced at each iteration of obtaining the consistent constrained dictionary. This effectively reduces the inter-column consistency， thereby improving the quality of the reconstruction results. Finally， the obtained consistent constrained dictionary was used as input for the SBL-VBEM model to reconstruct fabric images more effectively. The effectiveness of this approach was validated on the Alibaba Cloud Tianchi dataset. Experimental results demonstrate that the CCD-VBEM method achieves optimal performance in reconstructing fabric images at different sampling rates （0.20-0.40）， showcasing the potential of the algorithm in the field of fabric image reconstruction.

Keywords： fabric image; reconstruction; consistent constrained dictionary; variational Bayesian expectation maximization; shrinkage factor