核心素养视域下GeoGebra软件在高中数学课程可视化教学中的应用

新课标以培养学生学科核心素养为导向，将信息技术和数学教学内容有效结合，提高数学教学质量。GeoGebra（GGB）软件是一种动态化操作软件，涵盖几何、表格、图形、统计、代数、微积分等教学内容。在高中数学教学中充分利用GGB的动态表现形式和可视化功能，能将抽象的数学关系和数学问题以更加直观的方式展现出来，加深学生对数学知识的理解。

一、教材分析

“椭圆”选自人教版普通高中数学教科书A版，选修1第三章第3.1节。椭圆是生活中较为常见的圆锥曲线，但椭圆的形状与椭圆的定义之间并没有直接联系，需要以数学思维进行分析、推理，探究椭圆形状变化的本质。从学习地位来看，教材中这个单元按照教学先后划分，包括椭圆、双曲线以及抛物线三种类型。三类曲线都是按照几何特征、标准方程、方程中的曲线性质三个步骤由浅入深地进行研究，在研究内容、研究过程以及研究方式上具有极大的相似性。椭圆是研究的第一类曲线，对后续两类曲线的研究具有示范作用。因此，教师在教学中尤其要重视其蕴含的数学思想、研究基本方式以及逻辑思维方法等，为其他曲线的类比研究做好铺垫。

二、学情分析

高二学生已经具备研究直线和圆的方法和思想，具备研究椭圆及其标准方程的坐标法思想和数学运算方式等。但是在教学实践中，教师应该关注学生的数学抽象思想和运算能力，保证学生能准确掌握椭圆的定义。

三、教学方法

基于以上分析，笔者初步确定从几何的角度，利用坐标法来分析椭圆的标准方程及其几何性质。首先借助实验引导学生了解椭圆的几何特征和几何定义；其次从定义中推导椭圆的标准方程。在此过程中总结建立曲线方程的步骤，培养学生的数形结合、等价转化等数学核心素养，并理解椭圆方程中各个符号在几何中对应的含义，加强学生对椭圆定义的理解。主要应用的教学工具有GeoGebra软件、PPT、黑板。

四、教学过程

（一）问题引导，营造学习氛围

笔者首先在课堂上提问学生圆的定义，在学生举手回答后，笔者总结：圆是指到某一定点距离相等的点的轨迹，该定点为圆的圆心，定点到轨迹点的距离为半径。为了提高学生的学习兴趣，笔者利用GeoGebra软件引导学生学习，具体操作如下：

1.点击GeoGebra软件中的“定长线段”，弹出待输入点和线段长度的指令框。

2.根据指示在线段点位置处输入2，在长度位置输入AB，代表建立长度单位为2的AB定长线段。

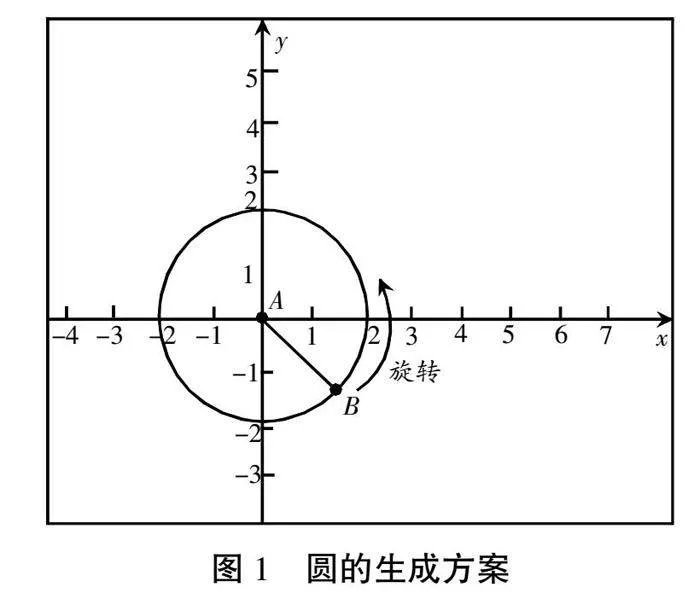
3.完成创建后，笔者直接在软件中进行演示，分别拖动线段的A点和B点，并组织学生观察、讨论随着笔者的拖动操作，在线段的A点和B点的移动中，线段分别产生了什么变化。学生观察后发现：拖动定长线段的点A，线段随着点A的移动而移动；拖动定点B，则B绕着点A转动。据此，笔者引出了B为动点的概念。

4.在软件中将动点B定义为“跟踪”，随后点击“启动动画”，点B自行围绕点A旋转，其运动轨迹形成圆，如图1所示。

（教学思路：在带领学生学习新的数学知识之前，对学生已经学习过的数学知识进行复习，一方面对原有知识进行强化，另一方面能激活学生原有知识结构中的坐标、图形等概念。同时在GeoGebra软件中进行演示，能激发学生的学习兴趣，引导学生积极参与课堂学习，为后期利用GeoGebra软件直观演示教学，培养学生的抽象思维、推理能力和想象力奠定基础。）

（二）继续变式教学，引入新的知识点

笔者首先利用PPT播放椭圆形状，引导学生从对圆形的直观感受转化为椭圆的直观感受。随后笔者以提问的方式鼓励学生猜想椭圆的定义。最后教师再利用GeoGebra软件引导学生深入探索椭圆的形成及其定义，具体操作方式为：

1.在软件中选择滑动条，建立变量并明确变量的取值范围，设变量为a。

2.以F1为圆心，绘制半径为2a的圆。

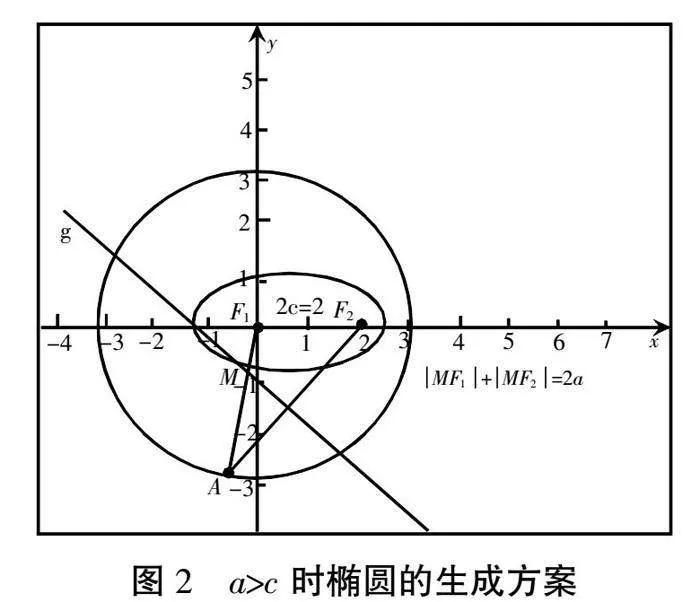
3.在绘制好的圆内任意选择一处F2，测量从圆心到圆内任意一点的距离2c。

4.在圆的轨迹上任意选择一点A，将点F2和点A相连并作出AF2的垂线，垂线与AF1相交于点M，得到MF2=AM，借此笔者引导学生思考MF1+MF2、MF1+AM、AF1、2a之间存在的关系，最后得出MF1+MF2=MF1+AM=AF1=2a。

5.在GeoGebra软件中，将点A作为控制动点，将点M作为追踪动点，随后点击“启动动画”生成M点的运动轨迹，如图2所示。

笔者引导学生观察由M点运动轨迹生成的图像，学生得出这一运动轨迹实际上是椭圆的结论。在此基础上笔者通过提问和小组讨论引导学生思考椭圆的数学特征，得出椭圆的定义为：在平面内到两定点距离之和等于定长（定长大于两定点间的距离）的动点的轨迹。

为了研究椭圆的定义，笔者在学生完成讨论后，继续操作GeoGebra软件：

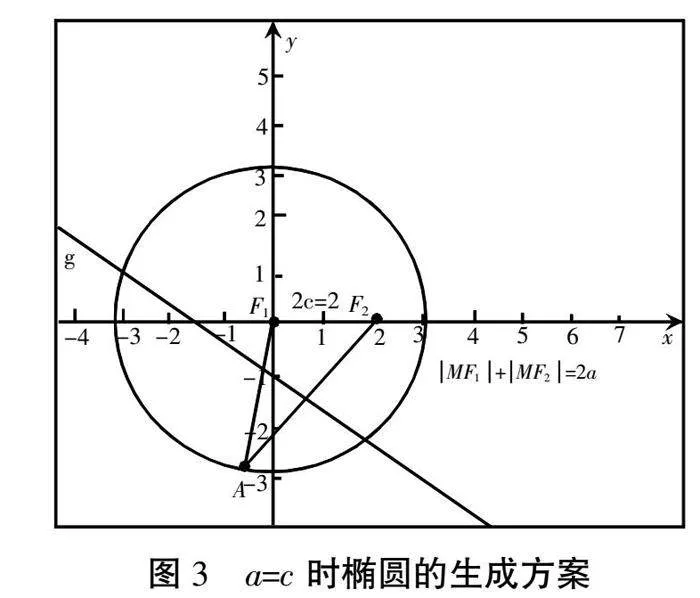
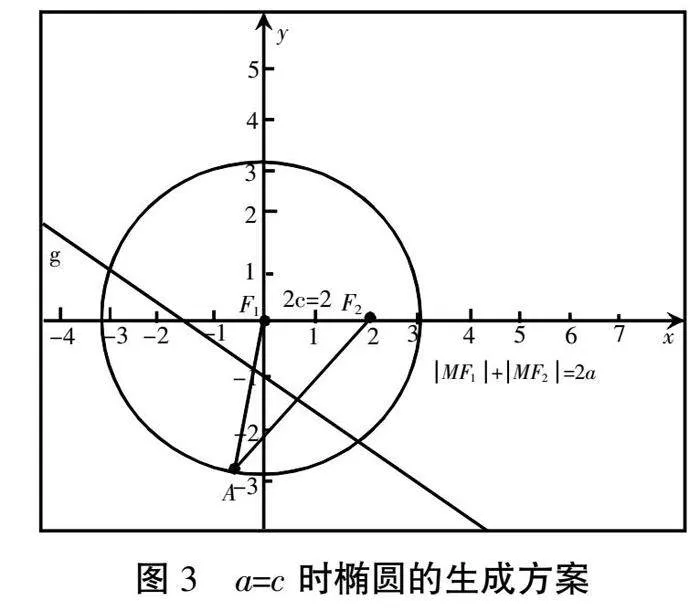
6.调整软件滑动条，以此改变量a值，带领学生从软件中直观观测随着a值的变化，图形的变化情况，随后提问并组织学生讨论2a和2c的值与图形之间的关系，最后笔者再进行总结：2a>2c>0时，图形为椭圆；2a=2c时，图形为圆，如图3所示。当2a<2c时，演示软件中AF2的垂线与AF1无法相交，并未形成图形，如图4所示。根据以上图形的变化，笔者在前期得到的椭圆定义基础上带领学生进一步完善，得到更为准确的椭圆定义为：在平面内的两个定点F1与F2之间存在的距离之和为常数2a，并且2a大于F1F2的绝对值2c时，由2a生成的点的运动轨迹为椭圆，并且称两个定点F1、F2分别为椭圆的左焦点和右焦点、F1F2即2c为焦距，从椭圆的定义中可以看出a>c>0。

（教学思路：在这一阶段的教学中，笔者首先利用GeoGebra软件将抽象的椭圆概念知识进行可视化演示，并利用动画生成功能直观演示椭圆的形成过程，不仅能集中学生的学习注意力，还能帮助学生理解椭圆背后蕴含的抽象数学概念，以降低学生理解的难度。）

GeoGebra软件以图形的方式直观地展示概念，学生能通过观察图像的变化和分析图像变化后的数学关系，理解椭圆的相关概念。在这一阶段，笔者在学生了解图像的变化后，主要以提问和小组讨论的方式组织学生自主概括其中的关联性，并尝试总结椭圆的概念。随后笔者再通过演示，让学生观察、分析椭圆的概念，对这个知识点进行循序渐进的理解。通过这一阶段教师可以有效培养学生的学科核心素养，包括数学抽象思维、逻辑推理能力以及想象能力等。

维果斯基的“最近发展区”理论强调教师开展教学活动时应该选择合适的工具协助学生尽可能减小最近发展区，让学生达到更高层次的学习水平，培养学生良好的数学思维能力。笔者在进行椭圆概念教学时，选择GeoGebra软件将抽象的椭圆概念知识转化为直观的椭圆图形变化问题，帮助学生初步感知椭圆的概念。之后，通过软件中的滑动条变化展示椭圆中a和c的变化及其与椭圆的关系，从而对学生的原有知识结构进行优化，在一系列教学活动中培养学生的交流能力、想象能力、抽象思维能力、逻辑思维能力等。

（三）知识的巩固和强化

（作者单位：溧阳市光华高级中学）

编辑：蔚慧敏