基于POA-RVM模型的抽蓄机组故障诊断

摘要：有效的故障诊断方法不仅能快速、准确地辨别抽蓄机组故障类型，还能降低抽水蓄能电站的运行维护成本。针对相关向量机（RVM）有关参数的调整不当导致诊断结果受影响的问题，提出利用鹈鹕优化算法（POA）对相关向量机参数的选取进行优化，构建鹈鹕优化算法和相关向量机组合的分类模型（POA-RVM）。选取仙居抽水蓄能电站4台抽蓄机组在5种状态下的数据进行预处理和特征选取后构成故障样本集，并分别采用标准相关向量机，以及用遗传算法、粒子群算法和灰狼算法优化的相关向量机模型对这些故障样本进行分类。结果表明：与标准相关向量机，以及经遗传算法、粒子群算法和灰狼算法优化的相关向量机模型相比，POA-RVM模型有效提高了抽蓄机组故障诊断的准确率。

关 键 词：抽蓄机组； 故障诊断； 相关向量机； 鹈鹕优化算法； 安全运行； 仙居抽水蓄能电站

中图法分类号： TV734

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2024.09.029

0 引 言

随着太阳能、风能、潮汐能等可再生能源的逐步开发，新能源发电在电网中所占比重日益增大，对电网的稳定运行造成了一定程度的影响［1-2］。抽水蓄能电站作为一种储能设施，对电网负荷调峰、填谷，改善电网运行条件，提高电网稳定性具有十分重要的作用［3-4］。

作为抽水蓄能电站的核心部件，水泵水轮发电机组的故障不仅会导致巨大的经济损失，还可能引发意外事故。因此，通过对抽蓄机组设备状态监测和故障诊断技术的进一步研究，可以及时掌握机组运行状态，对故障进行预测，有效降低设备损坏率，降低维护费用，从而提高机组的安全可靠性［5-6］。

在水电机组等旋转机械故障诊断领域，故障树（FT）、人工神经网络（ANN）、支持向量机（SVM）、相关向量机（RVM）等是应用最为广泛的故障分类算法。柳炀［7］采用故障树和概率神经网络（PNN）算法，通过分析抽蓄机组故障数据及其影响因素，诊断出抽蓄机组多种故障。闫双庆［8］采用小波变换方法对抽蓄机组不同工况下的振动信号进行处理并提取特征后，利用模糊聚类方法进行智能识别。Zhao等［9］采用反向传播神经网络（BPNN）对抽蓄机组在过度湍流、尾水管涡带振动、转轮中的过度振动等复杂运行状态进行了诊断识别。黎梓昕等［10］利用核主成分分析法（KPCA）对水轮机组噪声故障信号提取时域和频域特征后，采用PSO-SVM模型进行诊断和识别，从而得到高精度的分类结果。RVM是Tipping［11］提出的一种新算法，具有核函数选取范围广、泛化能力强和计算速度快等优点。而在RVM的应用过程中，超参数a、权重W和偏置B等参数的设置对分类效果影响较大，若选择不当可能会导致分类精度的下降。近年来，智能优化算法因采用非遍历式的方法，有助于计算成本的大大降低，被逐步应用到RVM超参数调整中。陈立伟等［12］利用遗传算法（GA）优化相关向量机的超参数，建立GA-RVM模型，并对燃机涡轮叶片故障进行分类，结果发现GA-RVM模型的分类精度高于SVM、标准RVM和BPNN。吕维宗等［13］提出了基于量子粒子群优化算法（QPSO）优化的相关向量机诊断模型，并采用此模型对轴承的振动故障进行诊断，有效提高了诊断效果。

虽然以上算法在精度上得以提升，但是这些算法存在调节参数多、容易陷入局部极值、迭代后期收敛速度慢等问题。因此，寻找一种性能更优并能有效应用于RVM参数优化的智能优化算法十分必要。鹈鹕优化算法（POA）具有参数少、结构简单等优点［14］。本文利用POA算法的优点提出了一种基于POA算法优化的POA-RVM模型，并采用该模型对抽蓄机组故障进行分类，弥补了传统群优化算法调节参数多、不易操作等不足。

1 相关向量机

RVM是一种监督学习算法，它是在稀疏贝叶斯学习理论的基础上，结合贝叶斯理论、Markov性质、最大似然估计和自动相关决定先验等理论提出的［15］。采用权重向量零均值的高斯先验分布来提高RVM模型的稀疏性，RVM的超参数采用最大化边缘似然函数的方法来估计。设xNi=1和tNi=1分别为训练样本的输入量和输出量，可得到目标t：

z=y（x）+εn（1）

y（x）=Ni=1Wi·K（x，xi）+B（2）

式中：εn为零均值方差σ2的噪声，K（x，xi）为核函数，B为偏置，B=W0，Wi为权重向量。

假设目标t是独立的，对其概率定义为

Ptw，σ2=（2πσ2）－N2exp－12σ2‖t－kw‖2

t=（t1，t2，…，tN）T，w=（w0，w1，…，wN）T

（3）

由于最大似然估计可能导致式（3）过拟合，因此在约束参数时采用了零均值高斯先验概率分布：

Pwa=∏Ni=0Nwi0，a-1i（4）

式中：a为超参数向量，a=（a0，a1，a2，…，aN）。

由贝叶斯理论可知，未知参数的后验概率表示如下：

Pw，a，σ2t=Pwa，σ2，t·Pa，σ2t（5）

其中后验分布的权重表达式如下：

Pwa，t，σ2=P（tw，σ2）P（wa）P（ta，σ2）=Nμ，

（6）

其中，

=（σ-2ΦTΦ+A）－1μ=σ－2ΦTtA=diag（a0，a1，…，aN）

（7）

式中：μ为后延均值，为协方差，A为超参数向量a的行列式值。为了实现统一的超参数，做出如下定义：

Pwa，t，σ2=（2π）－（N+1）2×－12exp－（w－μ）T－1（w－μ）2=Nwu，

（8）

2 鹈鹕优化算法

POA是由Pavel受鹈鹕狩猎行为启发而提出的一种新的元启发式优化算法［16］。鹈鹕确定猎物位置后，从10～20 m高空冲向猎物，并直扎入水中捕猎。这时，鹈鹕先张开大口，浮游前进，连鱼和水都进入囊中，然后闭口缩喉，将水挤出，鱼就会吞进肚子里［17］。

假设在一个M维搜索空间中，存在N只鹈鹕，第i只鹈鹕在M维搜索空间中的位置为Xi=［xi1，xi2，…，xim，…，xiM］，则N只鹈鹕组成的种群的位置X表示为如下形式：

X=X1X2XiXN=x11x12…x1m…x1Mx21x22…x2m…x2Mxi1xi2…xim…xiMxN1xN2…xNm…xNM（9）

式中：xim表示第i只鹈鹕在第m维的位置，在初始阶段它们在确定的范围内随机分布，即：

xim=Lm+Rd·Um－Lmi=1，2，…，N；m=1，2，…，M（10）

式中：Rd表示［0，1］之间的随机数，Lm和Um表示第i只鹈鹕在第m维位置的取值范围为［Lm，Um］。若在种群中的N只鹈鹕在M维搜索空间中的位置X作为适应度函数的变量，那么对应的适应度函数值FX可以表示为如下形式：

FX=F（X1）F（X2）F（Xi）F（XN）=f1f2fifN=f［x11x12…x1m…x1M］f［x21x22…x2m…x2M］f［xi1xi2…xim…xiM］f［xN1xN2…xNm…xNM］（11）

式中：F（Xi）表示第i只鹈鹕在M维搜索空间中位置Xi对应的适应度函数值。

在POA中，鹈鹕的捕鱼行为主要分为向猎物攻击和水上漂游2个阶段。

（1） 向猎物攻击阶段也称为探索阶段（P1）。在此阶段，鹈鹕确定猎物位置后从高空冲向猎物。猎物在搜索空间中的随机分布性增加了鹈鹕的探索能力，在每次迭代的过程中鹈鹕的位置更新描述为

XP1，t+1im=XP1，tim+Rd（Stm－λ·XP1，tim），FP1（XS）<F（Xi）XP1，tim+Rd（XP1，tim－Stm）， F（XS）≥F（Xi）（12）

式中：t表示当前迭代数；XP1，tim为在探索阶段P1第i只鹈鹕在第m维中的位置；Stm为猎物在第m维中的位置；λ取值为1或2的参数；F（Xi）表示第i只鹈鹕在M维搜索空间中的适应度函数值。如果目标函数的值在该位置上得到改善，则接受鹈鹕的新位置，这种更新叫做有效更新。为防止鹈鹕移到非最优区域，限制鹈鹕的移动，其对应的模型为

XP1，ti=XP1，ti，FP1i（XS）<F（Xi）XP1，tim，其他（13）

式中：XP1i为在探索阶段P1第i只鹈鹕的新位置，FP1i为在探索阶段P1第i只鹈鹕位置对应的目标函数值。

（2） 水面漂游阶段也称开发阶段（P2）。在这个阶段，鹈鹕在水面上展开翅膀，把鱼向上移动，然后把猎物放在喉咙袋里。鹈鹕在此过程中的这种行为描述为

XP2，t+1im=XP2，tim+γ·T－tT·2·Rd－1·XP2，tim（14）

式中：t表示当前迭代数；T表示最大的迭代次数；XP2，tim为在开发阶段P2第i只鹈鹕在第m维中的位置；γ为常数，在这里取值为0.2。同样，在开发阶段鹈鹕经过不断改变自己的位置来更新目标函数值。在此阶段为防止鹈鹕移到非最优区域，将限制鹈鹕的移动方向，其对应的数学模型如下：

XP2，ti=XP2，ti，FP2i（XS）<F（Xi）XP2，tim，其他（15）

式中：XP2i为在开发阶段P2第i只鹈鹕的新位置，FP2i为在探索阶段P2第i只鹈鹕位置对应的目标函数值。

根据上述描述，可知POA算法的计算流程如图1所示。

为了验证POA的优越性，本文选用了PSO、灰狼搜索（GWO）［18］与鲸鱼搜索（WOA）［19］算法分别对几个基准测试函数进行优化对比实验，基准测试函数名称及表达式如表1所列，其中F1和F2是单峰测试函数，F3、F4表示多峰测试函数。

分别采用PSO、GWO、WOA和POA算法独立运行表1的测试函数，计算出最优解、平均值和标准差等指标，其结果如表2所列。4种算法的种群规模、最大迭代次、独立运行次数等参数分别设置为30，1 000，20。

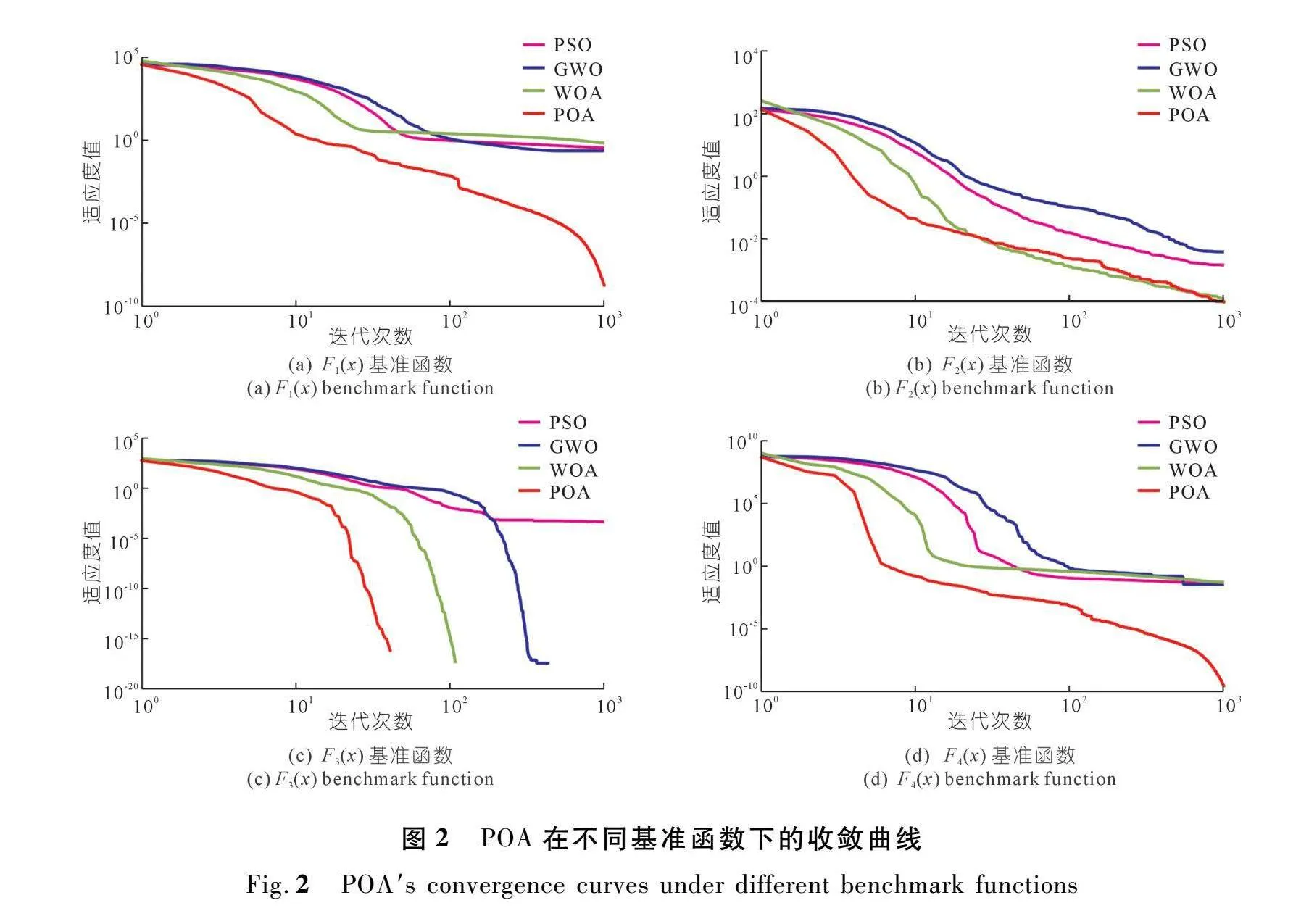
由表2可知，与PSO、GWO、WOA相比，POA的收敛精度更高。

POA在不同基准函数下的收敛曲线如图2所示。从图中可知，在几个基准函数中POA算法的收敛速度都快于PSO、GWO和WOA等算法。

3 POA-RVM模型

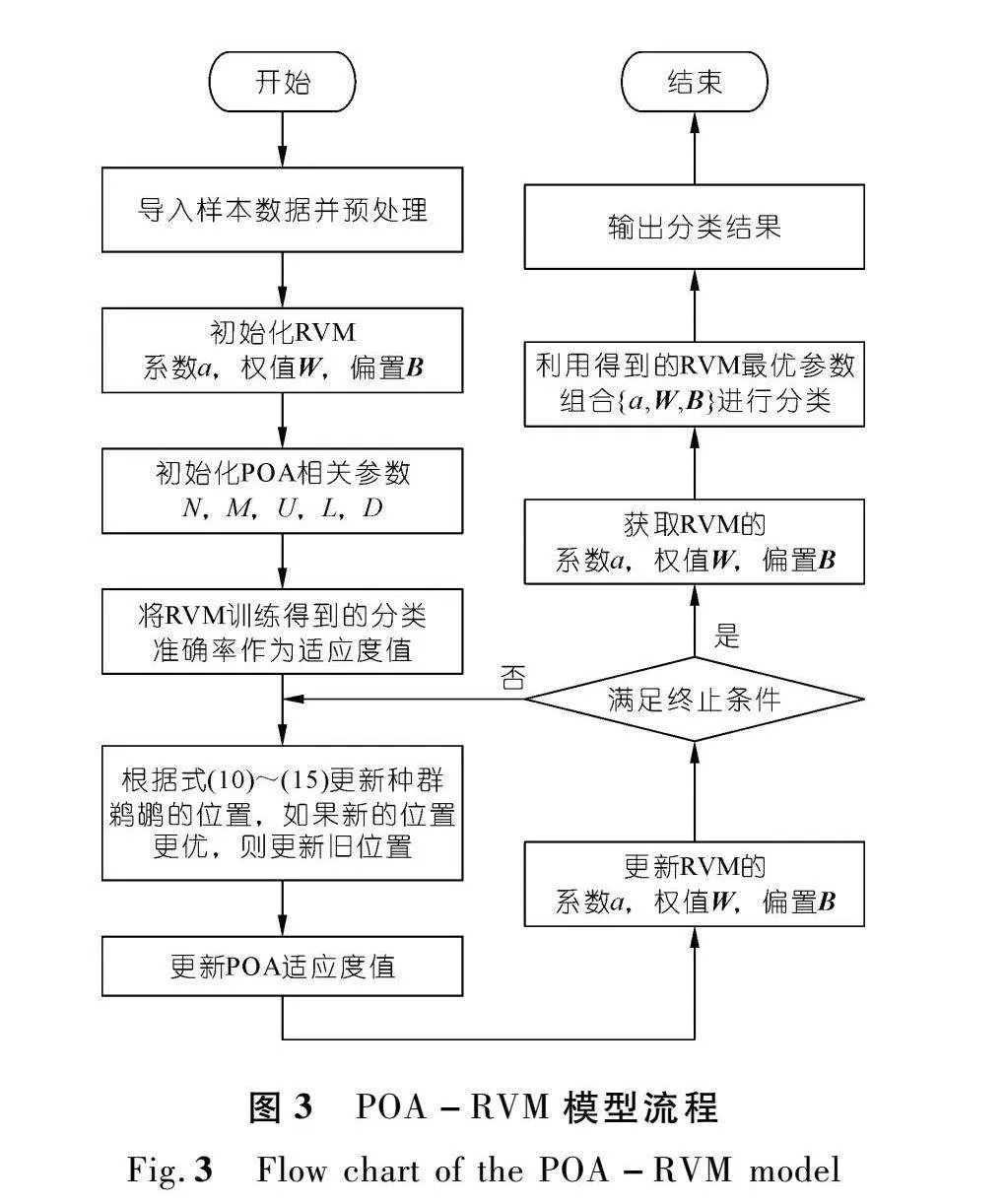
在RVM计算过程中，系数a、权重W和偏置B等相关参数的选取对分类结果有较大影响。在以往的参数设置中通常依据经验进行人工调整，因此难以找寻参数间的耦合关系，直接影响到最优参数组合的获得，进而影响到模型的精度。而通过POA优化RVM的系数a、权重W和偏置B等相关参数，可以有效获取最优的参数组合{a，W，B}，其相关的优化过程如图3所示。

POA-RVM诊断模型的具体计算步骤如下：

（1） 步骤1。对样本数据进行预处理，将其分为训练集和测试集后导入到算法中。

（2） 步骤2。初始化RVM的系数a、权重W和偏置B等相关参数。

（3） 步骤3。根据样本特征，设置POA算法的种群数量N、最大迭代次数M、自变量上限U、自变量下限L、维度D等相关参数。

（4） 步骤4。将训练得到的分类准确率作为适应度值，并按照系数a、权重W和偏置B的初始值训练RVM。

（5） 步骤5。采用公式（10）～（15）计算出鹈鹕当前位置相对应的适应度值，并与原值进行比较，如果新的适应度值更优，则替代原值。

（6） 步骤6。在RVM训练过程中当前的适应度值随鹈鹕位置变动而实时更新，不断保存最优的适应度值，以及其对应的RVM的系数a、权重W和偏置B。

（7） 步骤7。如果满足算法中设置的终止条件，则直接跳出该循环，同时输出RVM最优的参数组合{a，W，B}和对应的最优适应度值；如果不满足终止条件，则迭代次数自动加1，跳转执行步骤6。

（8） 步骤8。获取RVM的系数a、权重W和偏置B。

（9） 步骤9。使用选定的测试样本对RVM进行测试，输出分类结果。

4 实例分析

4.1 数据预处理

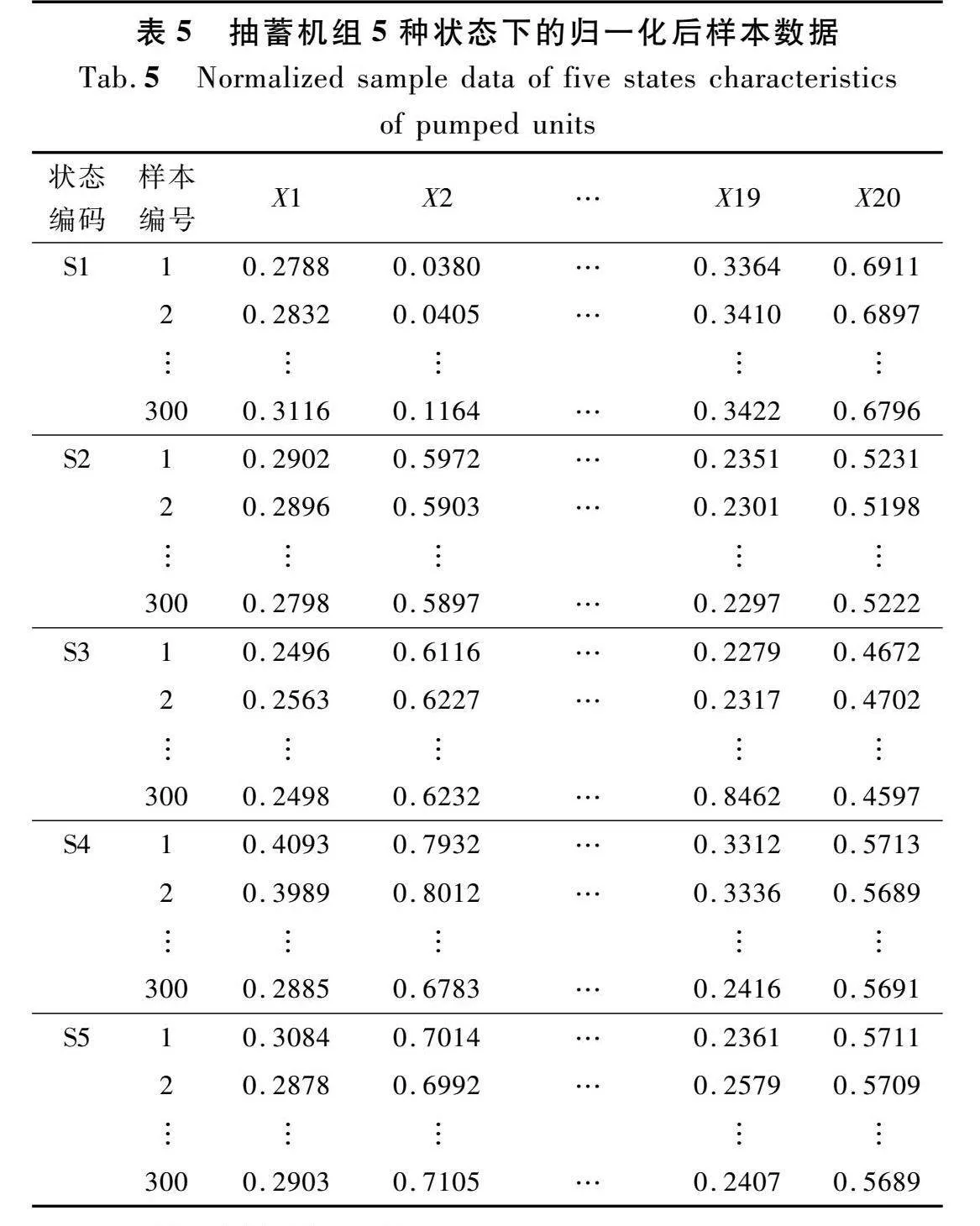
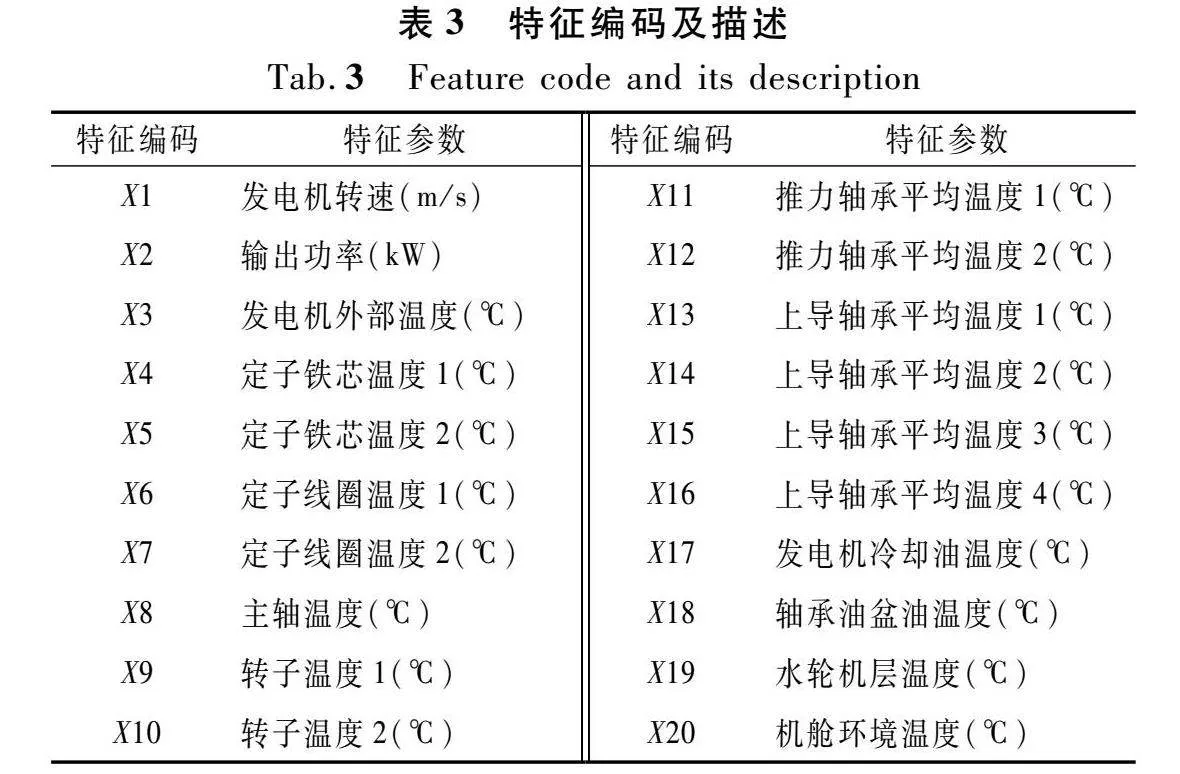
为验证POA-RVM诊断模型的性能，本文采用浙江省仙居抽水蓄能电站的4台抽蓄机组在5种状态下的相关数据作为试验数据，分别为发电机定子过热状态（S1）、发电机转子过热状态（S2）、推力轴承过热状态（S3）、上导轴承过热状态（S4）和正常状态（S5）。相关的特征参数如表3所列。

本次试验中，从5种状态中选取了1 500个样本，其中1 200个为训练样本，300个为测试样本，具体如表4所列。

分析之前，对样本进行预处理和归一化处理，归一化后的特征如表5所列。

4.2 模型性能比较

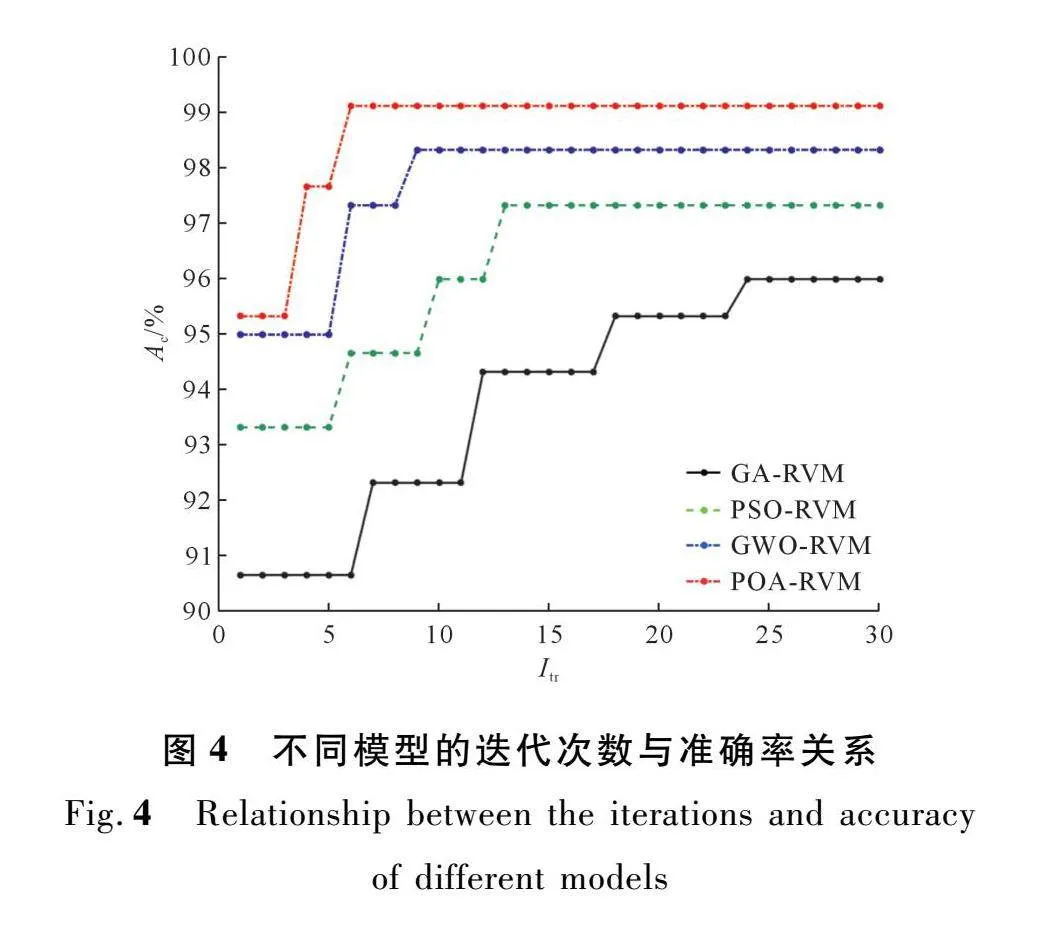
本文中，将POA-RVM与GA-RVM、PSO-RVM和GWO-RVM模型进行寻优适应度值比较，其结果如图4所示。图中，纵坐标Ac代表准确率，而横坐标Itr代表模型的运行次数。POA-RVM模型第6次运行时搜索到最优值（99.00%），GWO-RVM模型第9次运行时达到最优值（98.33%），PSO-RVM模型第13次运行时基本达到最优值（97.33%），而GA-RVM模型到达最优值（96.00%）需要运行到第24次。采用经POA算法参数优化后的RVM寻优速度最快且诊断准确率最高，GWO-RVM算法之次，而GA-RVM算法的效果最低。

SVM、RVM、GA-RVM、PSO-RVM、GWO-RVM、POA-RVM模型的分类结果如图5所示。图中，蓝色圆圈（○）表示实际类别，红色星星（＊）表示模型的预测类别，当实际类别和预测类别相同时，蓝色圆圈和红色星星相互重叠，重叠次数越多，表示该模型的分类精度越高。在图5（a）中，SVM模型把部分原属于S1、S2、S4和S5的样本误判为S2、S1、S2，蓝色圆圈和红色星星相互重叠次数最少，这表明SVM模型的分类效果不太好。在图5（e）中，POA-RVM模型完全正确分辨S2、S3、S4和S5，只有原属于S1的3个样本误判为S2，蓝色圆圈和红色星星相互重叠次数最多。结果表明，与其他模型相比，POA-RVM模型的分类效果最好。

为进一步显示POA-RVM模型的诊断性能，分别计算SVM、RVM、GA-RVM、PSO-RVM、GWO-RVM和POA-RVM等模型的精度（Pr）、召回率（Re）、F1值（F1）和准确率（Ac）等分类性能指标，其结果如表6所列。

从表中不难看出，当使用POA-RVM模型对抽蓄机组故障进行诊断时，除了误判3个发电机定子过热状态故障样本外，剩下的都正确识别，该模型的诊断准确率达到99.00%，均优于SVM、RVM、GA-RVM、PSO-RVM、GWO-RVM等模型，这表明POA-RVM模型能够较好地完成对抽蓄机组故障诊断的任务。

5 结 论

虽然RVM作为一种监督学习算法具有学习速度快、泛化能力强等优点，但其相关参数的设置将直接影响其分类效果，限制了其在故障诊断中的有效应用。针对这一问题，利用POA优化RVM相关参数值，可较大程度上弥补RVM模型的不足。本文研究结论如下：

（1） 采用POA优化RVM的相关参数，POA-RVM模型在测试集上的分类准确率可达到99.00%，且模型的分类性能指标均优于标准RVM、GA-RVM、PSO-RVM、GWO-RVM，有效提高了RVM的分类准确率和故障诊断性能。

（2） 在抽蓄机组的典型故障诊断中，虽然POA-RVM的分类准确率已经很高，但是对于一些复杂的故障情况仍然难以辨别。进一步研究更优的故障特征提取和特征选择方法，有助于提高该模型的分类精度。

参考文献：

［1］ XU W，DONG L，SHU Y，et al.Optimal sizing of energy storage in generation expansion planning of new power system with high penetration of renewable energies［J］.Energy Reports，2023，9（S7）：1938-1947.

［2］ 郑云平，焦春雷，亚夏尔·吐尔洪，等.基于新能源发电的构网型协调储能控制策略研究［J］.高压电器，2023，59（7）：65-74.

［3］ 张鹏，王俊星，段东晓，等.常规抽水蓄能电站电气主接线形式选择［J］.人民长江，2023，54（增1）：82-85.

［4］ 赵勇飞，卢小芳，瞿文鹏，等.长龙山抽水蓄能电站监控系统安全性设计［J］.水电站机电技术，2021，44（10）：60-61，73，179.

［5］ 姜爱军，孔令华，张涛，等.某大型抽水蓄能电站水泵水轮机转轮强度及模态分析［J］.水电与抽水蓄能，2023，9（1）：19-24.

［6］ 黄文龙，毕慧丽，叶永进，等.水泵水轮机开机过程水力特性研究［J］.水力发电学报，2023，42（2）：97-104.

［7］ 柳炀.基于故障树分析的水泵水轮机故障诊断方法研究及应用［D］.武汉：华中科技大学，2019.

［8］ 闫双庆.抽水蓄能机组运行状态分析与智能故障诊断研究［D］.武汉：华中科技大学，2019.

［9］ ZHAO W Q，EGUSQUIZA M，VALERO C，et al.On the use of artificial neural networks for condition monitoring of pump-turbines with extended operation［J］.Measurement，2020，163：1-13.

［10］黎梓昕，林海军，徐雄，等.基于KPCA-PSO-SVM的水轮机组故障检测方法［J］.排灌机械工程学报，2023，41（5）：467-474.

［11］TIPPING M E.The relevance vector machine［J］.Advances in Neural Information Processing Systems，2001，12：652-658.

［12］陈立伟，黄璐，齐传斌.基于遗传算法优化的相关向量机的燃机涡轮叶片故障诊断［J］.应用科技，2016，43（2）：70-74.

［13］吕维宗，王海瑞，舒捷.量子粒子群算法优化相关向量机的轴承故障诊断［J］.计算机应用与软件，2019，36（1）：6-11，16.

［14］XIONG Q，SHE J，XIONG J.A new pelican optimization algorithm for the parameter identification of memristive chaotic system［J］.Symmetry，2023，15（6）：1279.

［15］TROJOVSK P，DEHGHANI M.Pelican optimization algorithm：a novel nature-inspired algorithm for engineering applications［J］.Sensors，2022，22（3）：855-864.

［16］JOHN G T A.Foraging behavior of the american white pelican （Pelecanus erythrorhyncos） in western Nevada［J］.Colonial Waterbirds，1991（14）：166-172.

［17］O′MALLEY J，EVANS R.Kleptoparasitism and associated foraging behaviors in American White Pelicans［J］.Colonial Waterbirds，1983（6）：126-129.

［18］郭振洲，刘然，拱长青，等.基于灰狼算法的改进研究［J］.计算机应用研究，2017，34（12）：3603-3606，3610.

［19］张永，陈锋.一种改进的鲸鱼优化算法［J］.计算机工程，2018，44（3）：208-213，219.

（编辑：郑 毅）

Fault diagnosis of pumped storage units based on POA-RVM model

NI Jinbin1，XIAO Renjun2，SUN Huifang1，XIA Xin2，YU Shan1

（1.Pumped Storage Technology and Economic Research Institute of State GridXinyuan Co.，Ltd.，Beijing 100053，China； 2.Shandong Taishan Pumped Storage Co.，Ltd.，Taian 271000，China）

Abstract：

Effective fault diagnosis methods can not only quickly and accurately identify the fault types of pumped storage units，but also reduce the operation and maintenance costs of pumped storage power plants.To address the problem of improper parameters adjustment in the relevant vector machine （RVM） leading to the improper diagnosis results，we proposed to optimize selection of the parameters in the RVM by using the pelican optimization algorithm （POA），so a classification model combined with Pelican search algorithm and relevant vector machine （POA-RVM） was constructed.After preprocessing and feature selection of the data of four pumped storage units of the Xianju Pumped Plant under five states，a fault sample set was formed，and these fault samples were classified by using the standard RVM，and the RVM models optimized by genetic algorithm，particle swarm optimization algorithm，and gray wolf optimizer respectively.The results showed that compared with the standard RVM and variety of RVM models optimized by genetic algorithm，particle swarm optimization algorithm and gray wolf optimizer respectively，the POA-RVM model effectively improved the accuracy of fault diagnosis of pumped storage units.

Key words：

pumped storage unit； fault detection； relevant vector machine； pelican optimization algorithm； safety running