基于可解释性分析的大坝变形监控模型对比研究

摘要：近年来，经典统计模型和机器学习模型在大坝安全监控领域并行发展，然而前者的“预测能力”和后者的“可解释性”通常存在一定局限，且关于量化多重因素对大坝监测量影响程度的对比研究相对较少。基于闽江支流上GTX重力坝的水平位移和垂直位移原型监测数据，分别采用多元线性回归（MLR）、偏最小二乘回归（PLS）、随机森林算法（RF）建立兼顾预测能力和解释能力的大坝变形监控模型；同时，针对每种模型开展特征重要性分析，探究不同因素对大坝变形的影响程度。研究结果表明：3种模型中随机森林模型的拟合能力最佳，偏最小二乘回归模型的预测能力最佳；3种模型提供的可解释性基本符合实际规律，且特征重要性排序规律定性一致，水压分量和温度分量对该坝体位移影响显著，时效分量所占比例最低。研究成果可为后续开展大坝安全监控模型优选提供参考。

关 键 词：大坝； 安全监控； 机器学习； 统计模型； 特征重要性

中图法分类号： TV698.1

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2024.09.027

0 引 言

大坝作为国民经济中的关键基础设施，在发挥其显著经济效益的同时，亦面临多种因素损害其结构安全性，增加了运行故障的风险［1］。大坝变形是反映大坝总体工作性态的重要监测指标［2-3］，构建兼顾预测能力和可解释性的大坝变形监控模型，对于提升大坝的运行安全性和健康状况具有重大意义。

目前，广泛采用的大坝变形监控模型有3类：统计模型、确定性模型和混合模型［4］。统计模型利用历史监测数据，通过统计方法进行建模和分析。其中水位-季节-时效（hydrostatic-seasonal-time，HST）模型［5］是应用最广的大坝变形监控统计模型。在此基础上，广大学者对HST模型中水压、温度、时效3个分量的表达式进行了更加全面和细致的考虑［6-9］。然而，此类模型的准确性高度依赖于输入数据的质量，数据的误差或缺失将对预测和评估结果产生不利影响［10］。确定性模型的工作原理是基于物理和数学原理（如有限元）计算荷载作用下的变形场，然后根据实测值的统计分析求解调整参数［11-12］，其主要优点在于物理概念明确，可以更好地与结构性态相联系。此外，由于建立确定性模型不需要很长序列的实测数据，因此确定性模型适用于水库施工期和初蓄期。吴中如等［13］最先将确定性模型应用于佛子岭拱坝的监测资料分析中；李端有等［14］采用有限元法分别确定了隔河岩重力拱坝位移的水压位移分量和温度位移分量，并在此基础上建立了混凝土拱坝位移的一维多测点确定性模型。需要指出的是，准确的模拟结果需要大量真实、精确的输入数据，且确定性模型在处理未知或非线性动态行为时也存在一定的局限性。相对于统计模型和确定性模型而言，混合模型在建模时采用数值分析法来计算水压分量，采用统计方法来拟合计算温度分量和时效分量［15］。但此类模型的预测效果也受限于统计模型和确定性模型的局限，尤其是在数据量不足或数据质量较差的情况下［16］。魏博文［17］、黄万江［18］等构建了基于参数区间反演修正的单测点混合模型以及融合优化算法的多测点混合模型。

随着计算机技术和大数据的进步，机器学习已发展成为人工智能领域中最为活跃和成果丰富的研究分支。机器学习的目的是根据已知训练样本，让计算机从数据中自动学习、发现输入元素与输出元素之间的潜在规律，并通过对数据的分析和归纳来提高对未知数据的预测、分类或决策能力。Su等［19］将支持向量机应用于大坝变形预测中，有效地考虑到了大坝变形的非线性动力特性；王岩博等［20］提出了一种基于极限学习机的混凝土坝变形监测数据粗差识别方法，解决了连续时间序列数据中的粗差识别问题；吴云星等［21］提出了一种结合多种群遗传算法和反向传播神经网络的混合算法，旨在优化水工建筑物的定期变形监测预测；康俊锋等［22］将布谷鸟搜索算法和长短期记忆神经网络应用于大坝变形预测。尽管机器学习算法已在大坝安全监控领域取得了长足进步，但现有的大部分机器学习模型往往表现为“黑盒”模型，虽然可以根据输入给出相应的预测，但很难揭示其决策依据。此外，关于识别不同因素对大坝变形影响程度方面的研究相对较少。随机森林作为一种以决策树为基本结构的集成学习算法，能够计算出单个特征的重要程度，并可根据变量重要性度量对高维数据的特征进行选择，克服了“黑盒”模型的缺点。然而，采用随机森林模型对大坝变形监测数据进行分析和解释的研究并不常见。

为此，本文基于GTX重力坝的水平位移和垂直位移监测数据，分别采用多元线性回归（MLR）、偏最小二乘回归（PLS）、随机森林算法建立大坝变形监控模型；并在此基础上，定量分析不同因素对大坝变形的影响程度，对不同模型的估计结果进行对比分析，以期为大坝的长期服役和运行管理提供理论依据与决策支持。

1 算法模型

本文选用的3种模型均为兼顾预测能力和解释能力的模型，但计算原理以及特征重要性量化方法有所差异。

1.1 多元线性回归模型

多元线性回归的本质是研究多个自变量与一个因变量之间的相关关系，从而建立自变量与因变量之间的数学模型。其通用表达式为

Y=A+B1X1+B2X2+…+BnXn+ε（1）

式中：Y为因变量；A为回归模型常数项；X1～Xn为自变量；B1～Bn为回归模型未知参数；ε为随机误差。

在多元线性回归分析中，采用相对权重［23］来衡量自变量的相对重要度。先分别建立自变量与正交变量以及因变量与正交变量之间的线性回归模型，进而以两组线性回归系数平方和的乘积作为衡量自变量相对重要性的指标。其数学原理如下［24］：

（1） 将全部数据中自变量X构成n×m阶矩阵N，令P表示NNT的特征向量，Q′表示NTN的特征向量，得到相互正交的中间矩阵Z：

Z=PQ′（2）

（2） 建立因变量Y关于中间矩阵Z的多元线性回归方程，得到回归系数α：

α=ZTZ－1ZTY=QPTPQT－1QPTY=ITQPTY=QPTY（3）

（3） 因为正交变量互不相关，因此用α2表示中间矩阵Z对因变量Y的贡献比。为了精准表示自变量矩阵N对因变量Y的贡献比，建立自变量N关于中间矩阵Z的多元线性回归方程，得到回归系数χ：

χ=ZTZ－1Z′N=QPTPQT－1QPTPΔQT=I′QΔQT=QΔQT（4）

（4） 同理，可以用χ2表示中间矩阵Z对自变量矩阵N的贡献比，故自变量矩阵N对因变量Y的贡献比可表示为

ε=χ2α2（5）

因为自变量对因变量的贡献比是通过正交变换获得的，不仅解决了变量间的多重共线性问题，还反映了自变量对因变量的直接影响，包括自变量与模型中其他自变量的共同作用效应。因此可以使用各个自变量对因变量的贡献比来表示自变量对因变量的相对重要性。

1.2 偏最小二乘回归模型

偏最小二乘回归将多元线性回归、主成分分析、典型相关分析融为一体，通常用于处理自变量间的多重共线性问题。其基本原理如下［25］：

（1） 设有自变量X1，…，Xn构成的矩阵和因变量Y=（Y1，…，Yn）m×1构成的矩阵。对初始数据进行标准化处理从而避免量纲的影响，得到X标准化矩阵M0，Y标准化矩阵N0。

（2） 首先分别从M0、N0中提取第一成分t1和u1，t1和u1应尽可能大地代表X和Y中数据信息，且两者间相关系数应最大。然后分别建立自变量矩阵M0和因变量矩阵N0对t1的回归方程：

M0=t1pT1+M1（6）

N0=t1rT1+N1（7）

式中：p1=MT0t1‖t1‖2、r1=NT0t1‖t1‖2为回归系数向量，M1、N1为回归方程残差矩阵。

（3） 以M1和N1替代M0和N0，重复上述步骤直到满足迭代要求，得到：

M0=t1pT1+t2pT2+…+thpTh（8）

N0=t1rT1+t2rT2+…+thrTh（9）

最后得到：

y^=α1x1+α2x2+…+αpxp（10）

式中：αi（i=1，…，p）为偏最小二乘回归系数。

偏最小二乘算法通过变量投影重要性（VIP）原理解释自变量x作用于因变量Y时的重要性［26］，通过计算每个自变量对偏最小二乘模型中各成分的贡献程度，而这个贡献度反映的是各个自变量在构建偏最小二乘模型成分时的权重和这些成分对响应变量的解释程度，从而用得到的各个自变量的VIP值衡量变量重要性。其计算公式如下：

VIPj=p·Aa=1［qaY；th·ω2hj］Aa=1qaY；t1，…，th（11）

式中：VIPj表示第j个特征对应的VIP值；p为预测变量总数；A为偏最小二乘成分总数；qa（Y；th）表示th轴对Y的解释能力；ωhj表示轴的第j个分量，用于测量xj对构造th的边际贡献；qa（Y；t1，…，th）表示轴t1，…，th对Y的累积解释能力。

1.3 随机森林模型

随机森林回归算法模型是一种集成多棵决策树的强学习器模型［27］，通过将随机子空间方法和Bootstrap集成学习理论结合，用以数据挖掘和机器学习。其基本原理如下：

（1） 对于输入的数据集进行提取，划分拟定的因变量与自变量并形成原始样本集。

（2） 利用Bootstrap的重抽样技巧，在原始样本集中执行有放回的随机提取，以此创建若干个独立的样本集。对于每个独立样本集，既包括被随机选出的数据，也包括那些未被选出的数据（称为袋外数据），这两部分数据共同参与构造成一棵独立的决策树。

（3） 在构建每一棵决策树时，系统在全部N个特征（即自变量）中随机选取m个特征来决定树的分支条件。根据增益（Gain）指标从这m个特征中挑选出最佳的分裂点进行节点的分裂，以确保树能够以最充分的方式成长，进而建立回归决策树。

（4） 对于输入的自变量Xi（i=1，2，…，n），每棵决策树都会生成一个预测值Yi，所有决策树预测值的平均值即为最终输出的预测结果。同时此前决策树未抽取到的数据集可用来验证真实值与预测值的误差。

随机森林回归算法通过计算每棵树对应的袋外数据误差，随机对袋外数据所有样本中的特征Xi加入噪声干扰，然后重新计算误差，并分析袋外数据同一特征加入噪声前后的误差变化幅度，变化幅度越大说明该特征对预测结果即因变量的影响越大，也表明其重要性越高。

2 实例分析

研究实例为中国福建省境内闽江支流上GTX混凝土宽缝重力坝，其最大坝高71 m，坝顶高程384.5 m。针对该坝20号坝段坝顶监测点的水平位移数据和15号坝段坝顶监测点的垂直位移数据，分别建立多元线性回归模型、偏最小二乘回归模型以及随机森林模型。将位移以及相对应的自变量数据集划分为两组，前70%数据用来训练模型（训练集），后30%数据用来测试模型（测试集）。根据水位-季节-时效（HST）模型［5］，选取H、H2、H3、H4、sin2πt365、cos2πt365、sin2πt365·cos2πt365、θ和lnθ共9个变量作为影响因子变量［2］，其中H为上游水深，t为观测日至观测基准日的累计天数，θ=t100。

2.1 预测结果分析

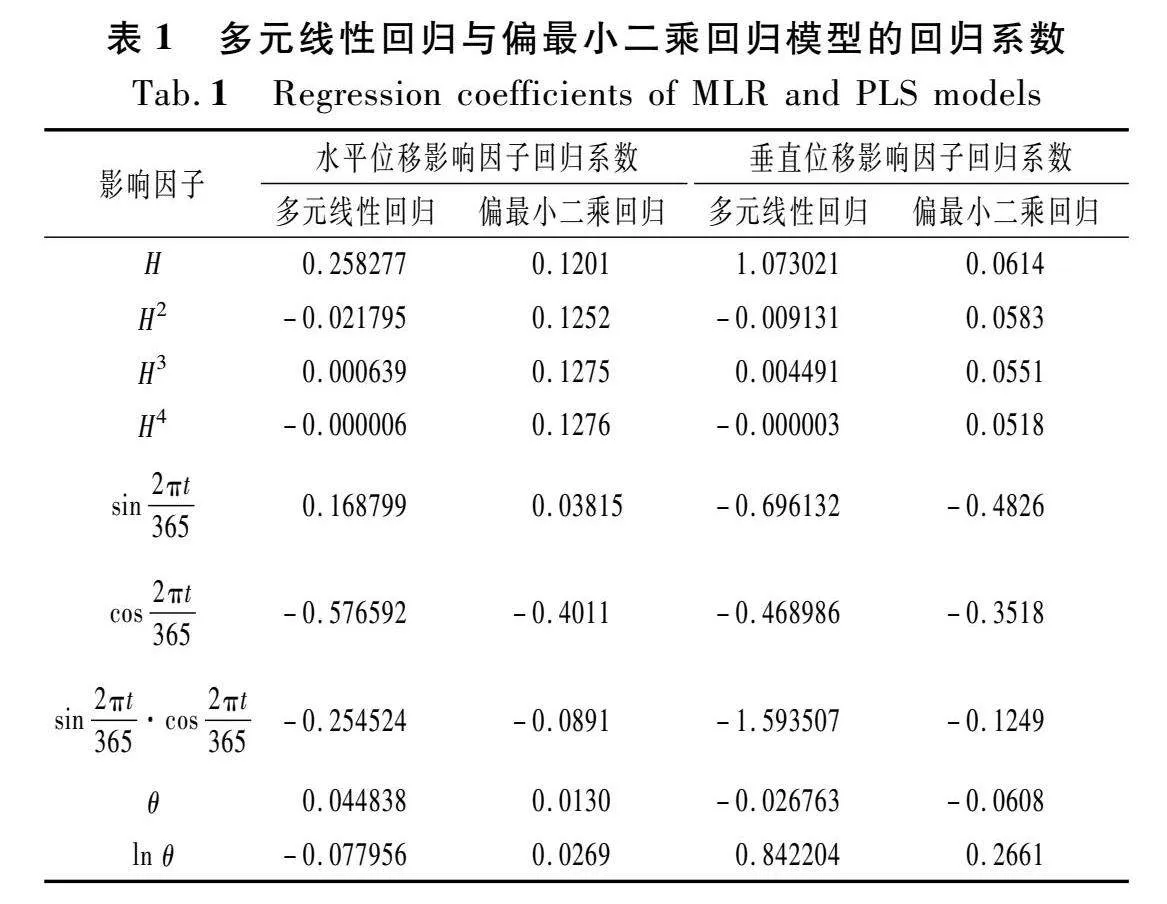
基于监测数据建立多元线性回归模型、偏最小二乘回归模型和随机森林模型，其中，由MLR和PLS模型得到的回归系数结果见表1。由表1可知，根据两种不同方法所确定的回归系数通常存在较大差异。例如，4个水位因子呈幂次关系，系数符号该保持一致，而在多元回归中，系数有正有负，并不合理；相比之下，偏最小二乘回归的系数同号且均为正数，表明上游水深增大，坝体水平位移向下游变化，与大坝实际变形规律相符。引起这种差异的主要原因在于偏最小二乘回归模型较好地解决了模型中各自变量因子高度相关的问题，使得大坝水位、温度和时效变量在解释监测效应量上更加严谨。

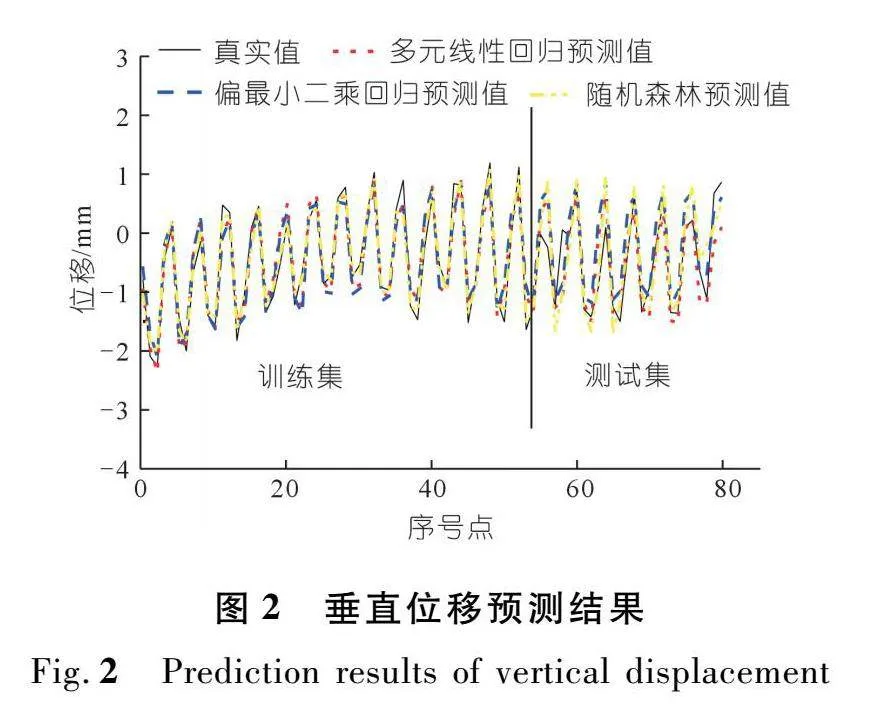
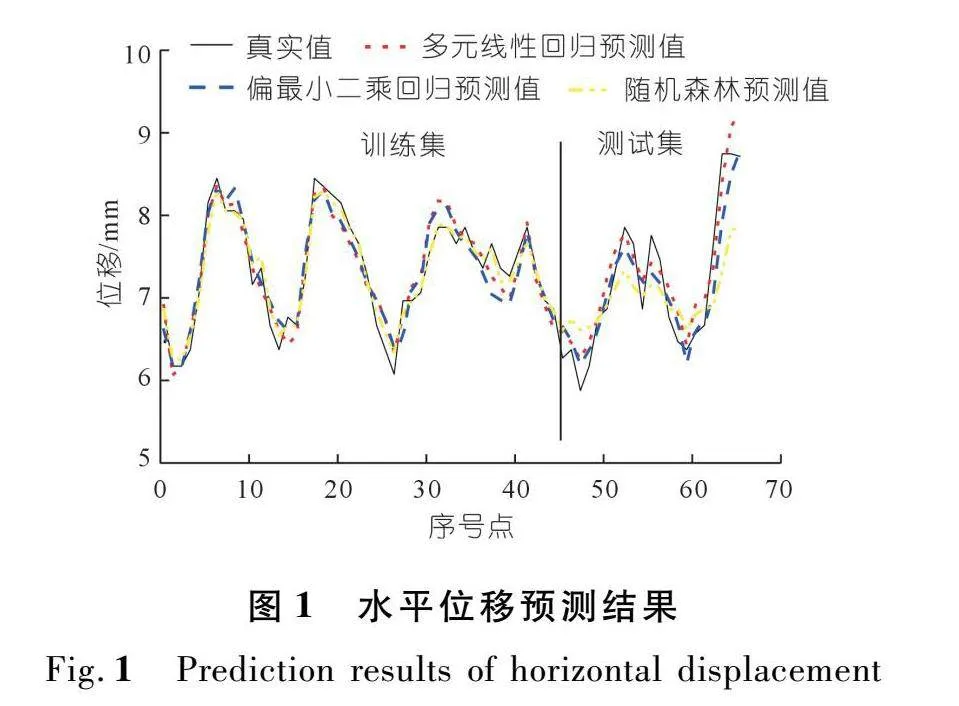
基于3种模型，进一步确定训练集的拟合精度和测试集的预测精度。图1和图2分别给出了水平位移和垂直位移的“预测值与实测值”对比结果。可以发现，3种模型预测的位移值大体上与实测值变化规律一致，但在部分“转折点”上存在相对较大差异。结合前文对回归系数的分析可知，自变量之间的相关性对模型回归的拟合效果影响不大，但对模型回归系数的影响较大，这与之前的研究结论［28］相符。

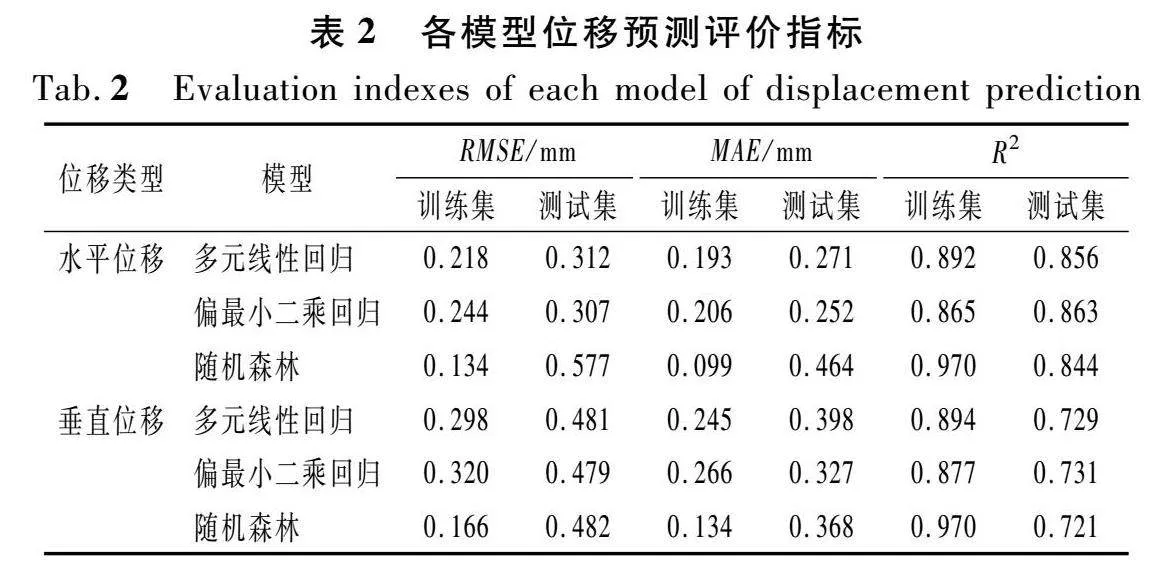
采用均方根误差RMSE、平均绝对误差MAE和决定系数R2作为模型评价指标，将结果汇总于表2。

从表2可以发现，在训练集中，随机森林模型的拟合能力优于多元线性回归和偏最小二乘回归模型。以水平数据为例，随机森林模型的R2最大，RMSE和MAE均最小，相较于其他两种统计模型，其RMSE和MAE分别降低约40%和50%。然而，在测试集中，偏最小二乘回归模型展示出较高的准确性，其预测性能优于其他两种模型。具体而言，偏最小二乘回归模型的RMSE和MAE分别比多元线性回归和随机森林模型降低1.6%和46.8%、7%和45.7%。

需要指出的是，3个评价指标具有不同的内在含义。例如，与MAE相比，由于RMSE对残差项进行了平方，因此该指标往往对大残差更为敏感，这意味着RMSE更容易受到部分离群值的影响。综上，偏最小二乘回归模型的预测能力优于其他两种模型，多元线性回归模型次之，随机森林模型的预测精度相对较低，这可能与当前样本数量有限有关。

2.2 影响因素重要性分析

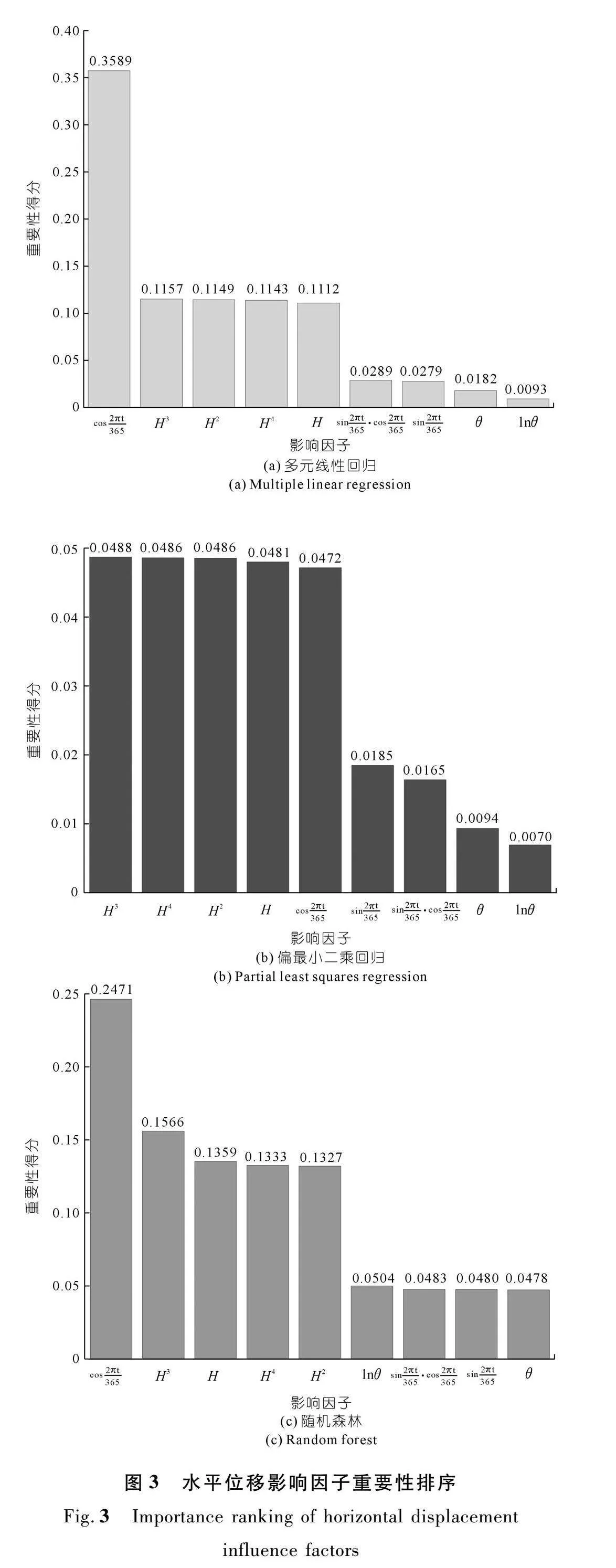
根据前文不同模型的特征重要性计算方法，以多元线性回归模型运用相对权重的思想对水平位移监测数据进行特征重要性分析为例，首先得到按不同顺序剔除某个变量后的R2，例如按不同顺序剔除影响因子H后，回归得到的R2分别为0.452 3，0.272 7，0.149 5，0.072 7，0.030 6，0.011 7，0.006 1，0.004 8，0；其次根据每个变量的R2之和等于多元线性回归的总R2，对上述9个结果取平均值，可以得到影响因子H的重要性得分为0.111 2。3种模型所得结果如图3～4所示。可以发现，尽管模型不同，但所确定的分量得分排序规律基本一致。此外，对于不同模型，同一分量（如水压分量）中不同因子的相对排序可能有所差异。

由图3可知，针对该混凝土重力坝，温度影响因子cos2πt365在多元线性回归模型和随机森林模型中的重要性排名第一；4个水压因子在偏最小二乘回归模型中排名前四，在其余两个模型中均排在第2～5位；而时效因子的影响相对较小，在3个模型中其重要性得分远低于水压分量和时效分量。由图4可知，对于垂直位移，水压分量的影响最大，4个代表水压分量的影响因子在每个模型重要性排序中均在前4位；其次是温度分量；相比之下，时效分量的重要性得分明显小于前两者。该结论与以往监测资料分析中得到的重力坝测点变形规律亦相符。

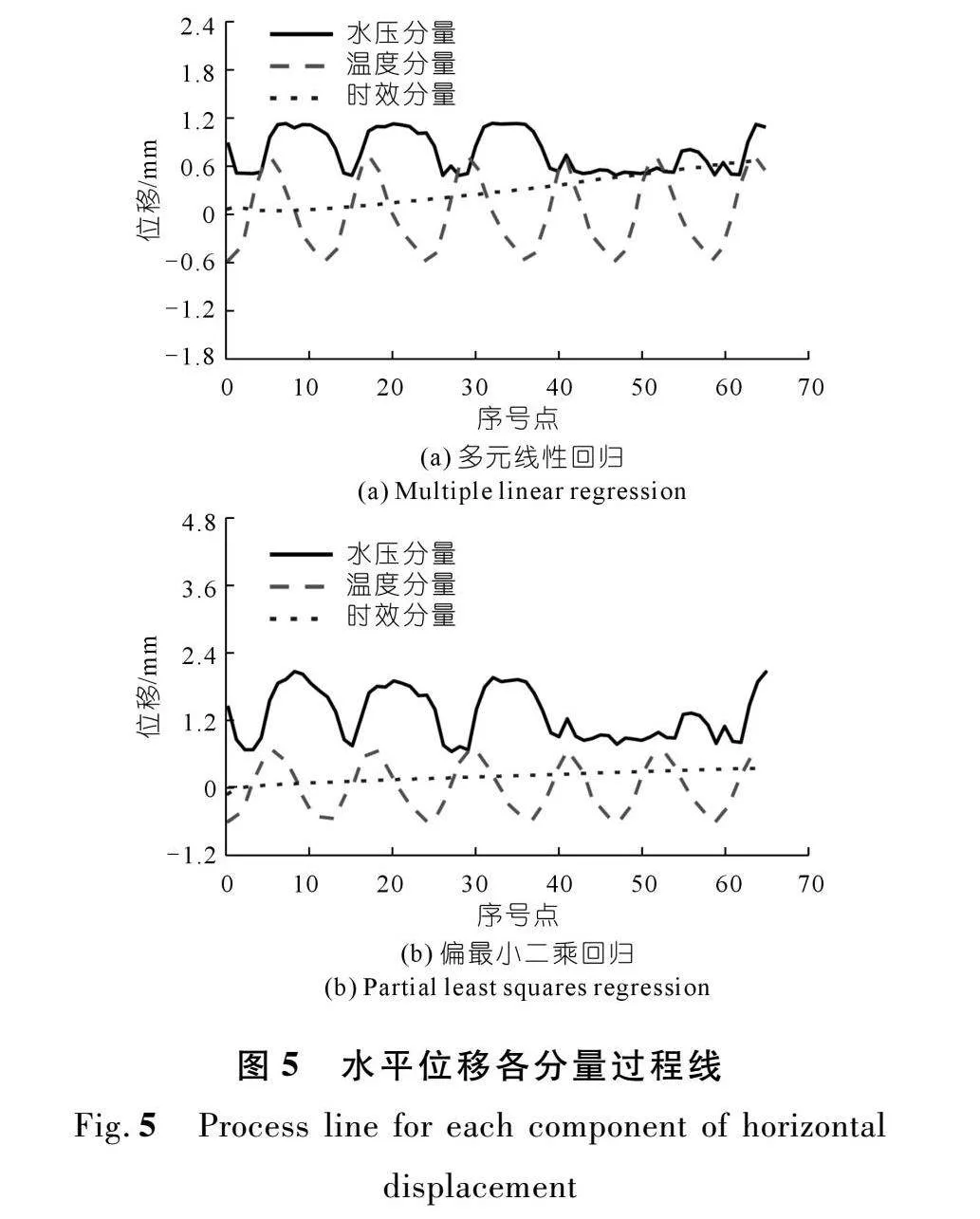
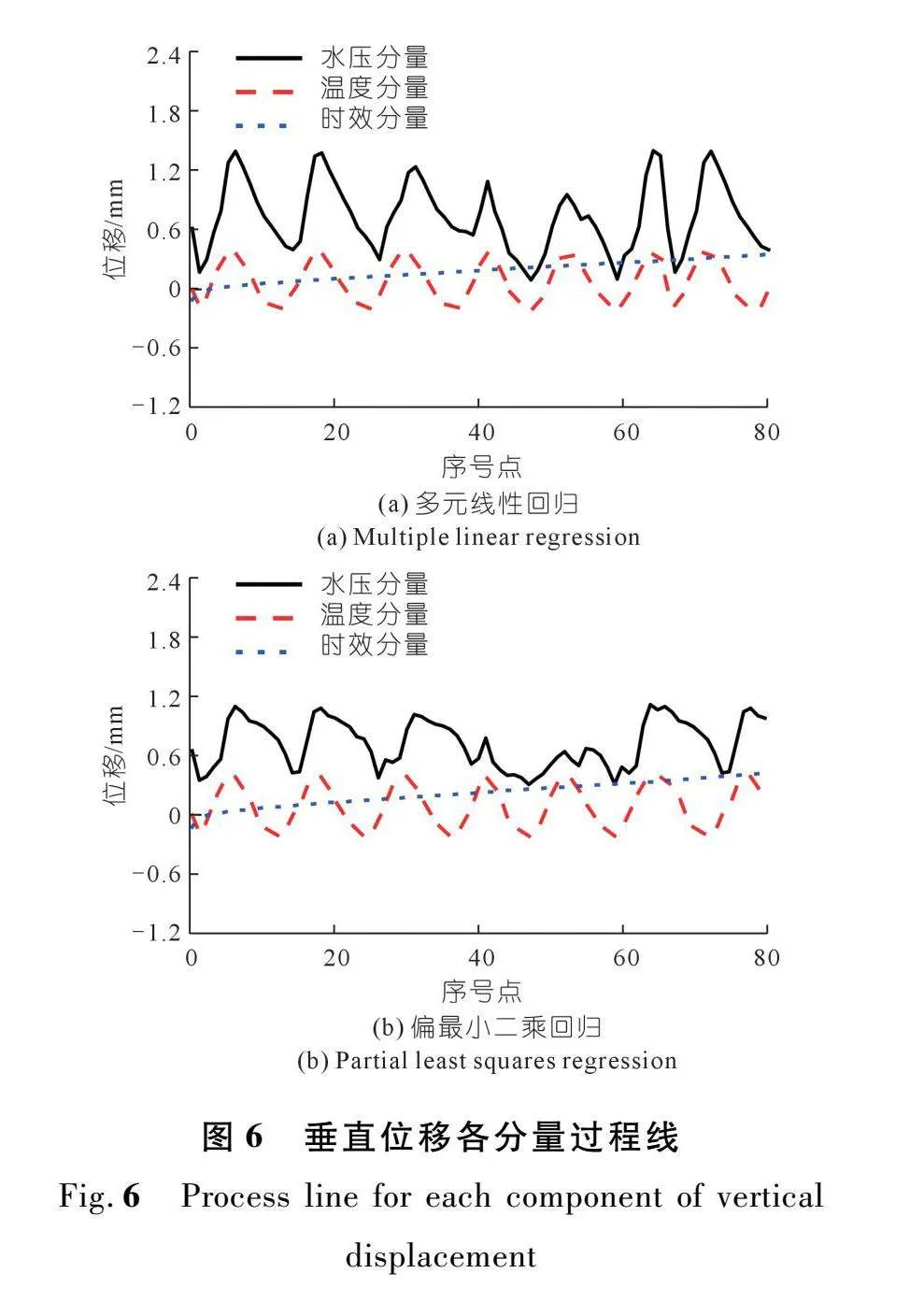
为进一步验证特征重要性分析结果，图5～6分别给出了多元线性回归模型和偏最小二乘模型所得的各分量过程线［28-29］。可以看出，无论水平位移还是垂直位移，水压分量和温度分量均占有较大的比例，时效分量所占比XFbXiOhBMXP3jSx7WYtg5g==例最小。但与图5～6相比，图3～4的特征重要性分析结果更为直观且更易量化。

综上，特征重要性分析是为模型提供可解释性的重要工具，不同自变量影响因子对水平位移和垂直位移的影响程度可能有所区别。结合水平和垂直位移的特征重要性分析可以发现，对于该混凝土重力坝，水压分量和温度分量是位移的主要影响因素。

3 结 论

本文以GTX混凝土重力坝的变形监测数据为研究实例，分别对多元线性回归模型、偏最小二乘回归模型和随机森林模型的预测能力和可解释性进行了对比分析。

研究结果表明：对于训练集，基于决策树算法的随机森林模型能够更加有效地捕捉数据中的复杂非线性关系，其评价指标R2最高，RMSE和MAE均最低；对于测试集，偏最小二乘回归模型的表现最佳。特征重要性分析结果表明，3种模型的分析结果定性一致：水压分量和温度分量对坝体位移影响显著，时效分量影响较小。模型提供的可解释性符合大坝变形规律，与传统分量过程线法相比，特征重要性分析结果能够更加直观地反映不同自变量对坝体位移的影响程度。研究成果可为后续开展大坝安全监控模型优选提供参考依据。

参考文献：

［1］ 吴中如，陈波.大坝变形监控模型发展回眸［J］.现代测绘，2016，39（5）：1-3，8.

［2］ 吴中如.水工建筑物安全监控理论及其应用［M］.北京：高等教育出版社，2003.

［3］ 易正元，苏怀智，杨立夫.混凝土坝变形监控模型的随机森林与旗鱼优化组合建模方法［J］.水电能源科学，2021，39（10）：106-109，143.

［4］ 黄华东，郭张军.大坝安全智能监控模型对比分析研究［J］.中国水运（下半月），2019，19（6）：71-73.

［5］ WILLM G，BEAUJOINT N.Les me′thodes de surveillance des barrages au service de la production hydraulique d′Electricite′ de France-Proble`mes ancients et solutions nouvelles［C］∥IXth international congress on large dams，1967：529-550.

［6］ WANG S，XU Y，GU C，et al.Hysteretic effect considered monitoring model for interpreting abnormal deformation behavior of arch dams：a case study［J］.Structural Control and Health Monitoring，2019（3）：e417.

［7］ PIERRE L，LECLERC M.Hydrostatic，temperature，time-displacement model for concrete dams［J］.Journal of Engineering Mechanics，2007，133（3）：267-277.

［8］ SALAZAR F，TOLEDO M A.Discussion on "thermal displacements of concrete dams：accounting for water temperature in statistical models"［J］.Engineering Structures，2015，171：1071-1072.

［9］ LI F，WANG Z，LIU G，et al.Hydrostatic seasonal state model for monitoring data analysis of concrete dams［J］.Structure & Infrastructure Engineering，2015，11（12）：1616-1631.

［10］李富强.大坝安全监测数据分析方法研究［J］.杭州：浙江大学，2012.

［11］王小敏，刘小勇.大坝变形分析与预报的有限元法［J］.地理空间信息，2009，7（5）：127-130.

［12］许昌，岳东杰，董育烦，等.基于主成分和半参数的大坝变形监测回归模型［J］.岩土力学，2011，32（12）：3738-3742.

［13］吴中如，范树平.佛子岭连拱坝原型结构性态综合分析［J］.水利水电技术，1993（11）：2-6.

［14］李端有，周元春，甘孝清.混凝土拱坝多测点确定性位移监控模型研究［J］.水利学报，2011，42（8）：981-985，994.

［15］顾冲时，吴中如.大坝与坝基安全监控理论和方法及其应用［M］.南京：河海大学出版社，2006.

［16］任超，梁月吉，庞光锋，等.最优非负变权组合模型在大坝变形中的应用［J］.大地测量与地球动力学，2014，34（6）：162-166.

［17］魏博文，袁冬阳，李火坤，等.基于参数区间反演修正混合模型的混凝土坝位移监控指标确定方法［J］.岩石力学与工程学报，2018，37（增2）：4151-4160.

［18］黄万江.混凝土拱坝多测点变形监控混合模型研究［J］.水利技术监督，2023（4）：13-15.

［19］SU H，LI X，YANG B， el al.Wavelet support vector machine-based prediction model of dam deformation［J］.Mechanical Systems and Signal Processing 2018，110：412－427．

［20］王岩博，顾冲时，石立，等.基于改进IGGⅢ-ELM法的混凝土坝变形监测数据粗差识别方法［J］.水利水电科技进展，2023，43（6）：89-95.

［21］吴云星，周贵宝，谷艳昌，等.基于LMBP神经网络的土石坝渗流压力预测［J］.人民黄河，2017，39（8）：90-94，148.

［22］康俊锋，胡祚晨，陈优良.基于布谷鸟搜索算法优化LSTM的大坝变形预测［J］.排灌机械工程学报，2022，40（9）：902-907.

［23］JEFF W.A heuristic method for estimating the relative weight of predictor variables in multiple regression［J］.Multivariate Behavioral Research，2000，35（1）：1-19.

［24］代鲁燕，沈其君，张波，等.相对权重法在线性模型自变量相对重要性中的估计及其应用［J］.中国卫生统计，2013，30（1）：19-20，22.

［25］王惠文.偏最小二乘回归方法及其应用［M］.北京：国防工业出版社，1999.

［26］BENJAMIN M，MOSTAFA E Q，BENOT J.Extension and significance testing of variable importance in projection （VIP） indices in partial least squares regression and principal components analysis［J］.Chemometrics and Intelligent Laboratory Systems，2023，242：104986.

［27］BERIMANL.Random forests［J］.Machine Learning，2001，45（1）：5-32.

［28］徐洪钟，吴中如.偏最小二乘回归在大坝安全监控中的应用［J］.大坝观测与土工测试，2001（6）：22-23，27.

［29］何金平.大坝安全监测理论与应用［M］.北京：中国水利水电出版社，2010.

（编辑：胡旭东）

Comparison of monitoring model for dam deformation based on interpretability analysis

HUANG Haiyan1，AI Xingxing2，LIU Xingyang2，LI Zhanchao2，QIU Jianchun2

（1.Yunnan Water Resources and Hydropower Vocational College，Kunming 650499，China； 2.College of Hydraulic Science and Engineering，Yangzhou University，Yangzhou 225100，China）

Abstract：

In recent years，classical statistical models and machine learning models have parallelly developed in dam safety monitoring field.However，the predictive ability of the former and the interpretability of the latter usually have certain limitations，and there are relatively few comparative studies on the impact of quantitative multiple factors on dam monitoring measured data.Based on the prototype monitoring data of horizontal displacement and vertical displacement of GTX gravity dam on the tributary of Minjiang River，this paper used multiple linear regression （MLR），partial least squares regression （PLS） and random forest algorithm （RF） to establish different dam deformation monitoring models that takes both predictive ability and interpretability into account.At the same time，the feature importance analysis was carried out for each model to explore the influence of different factors on dam deformation.The results showed that the random forest model had the best fitting ability and the partial least squares regression model had the best prediction ability among the three models.The interpretability provided by the three models was basically in line with the actual law，and the order of feature importance was consistent：the water pressure component and the temperature component had a significant impact on the displacement of the dam body，and the proportion of the aging component was the lowest.The research results can provide reference for the subsequent optimal selection of dam safety monitoring model.

Key words：

dam； safety monitoring； machine learning； statistical model； feature importance