典型平推式滑坡水力分布规律及启动机理研究

摘要：平推式滑坡形成于近水平岩层中，地下水对平推式滑坡的启动和运动过程影响非常显著。为揭示平推式滑坡滑动面上水力分布与滑坡启动的相关性，以成都市狮子山滑坡为地质原型，自主研制试验设备，进行水力测试试验，测试近水平倾角（0°～10°）条件下，底滑面两种不同连通条件下不同位置的水压力，研究底滑面承压水压力分布规律及启动机理。结果表明：① 底滑面渗流条件较差或滑坡前缘堵塞条件下，水压力分布呈现梯形分布；流通条件下，水压力在底滑面方向上呈曲线下降，自后缘至剪出口下降速率先增大后减小，底滑面倾角越增大，下降速率变化越显著。② 层间裂隙水扬压力值比传统采用三角分布形式的扬压力值小约27.6%。③ 薄层状泥岩的软化、变形是滑坡启动的根本原因；暴雨情况下底滑面扬压力和后缘裂隙中高水压下的水平推力联合作用将滑体推出是滑坡启动的直接原因。研究结果对平推式滑坡的稳定性分析评价和治理方案确定具有一定参考和借鉴价值。

关 键 词：平推式滑坡； 水力分布； 承压水； 孔隙水压力； 启动机理； 工程地质

中图法分类号： P642.22

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2024.09.020

0 引 言

在传统极限平衡法中，一般认为岩层近水平滑坡是稳定的，不具备破坏条件。而四川盆地红层覆盖区却广泛发育着一种岩层产状近水平的岩质滑坡，如川中垮梁子滑坡、宣汉县天台乡滑坡、南江县千邱塝滑坡均为此类型滑坡。这类滑坡多在暴雨条件下发生，由岩体风化裂隙中的水对滑体的向前推力和滑移面向上的浮托力提供力学基础。水的力学作用大大降低了滑坡稳定性，当裂隙中水位超过临界值时，滑体在水力作用下推出，故称此类滑坡为平推式滑坡。

张倬元［1］、王兰生［2］等最早提出平推式滑坡的概念，他们基于四川盆地红层地区大量滑坡实例分析指出，此类滑坡是以塑流-拉裂变形为主，在后缘裂Q3PSOuWnGuTZNQpiHHHDQA==隙和滑移面中水的推力和浮托力联合作用下产生的一种暴雨启动型滑坡，并提出平推式滑坡的启动判据。殷坤龙等［3］通过对万州区近水平地层滑坡和堆积体成因机制的研究，提出静水压力诱发平推式滑坡的主要因素。上述研究总结了平推式滑坡的基本特征，指出裂隙中水的动力因素在平推式滑坡成因机制中具有重要作用，但并未对其破坏机制以及水动力影响进行深入分析以及验证。

近年来，平推式滑坡相关研究逐渐丰富。在平推式滑坡启动机制的研究中，对后缘裂隙水的作用形式、滑带土在水作用情况下力学性质劣化等方面均有较为深入的研究。范宣梅［4］、郭晓光［5］等通过物理模拟方法对天台乡滑坡、垮梁子滑坡等多级平推式滑坡的形成过程模拟并分析其成因机理，将平推式滑坡滑动过程分为蠕滑启动、平推快速滑动、减速制动3个阶段，并对张倬元等［1］提出的判据进行了验证。张明等［6］对青宁乡滑坡进行数值模拟研究发现，暴雨是滑坡启动的必要条件，启动后滑带的抗剪强度急剧下降，导致滑体加速运动。蒋宇等［7］对红层滑坡特征矿物进行物理化学分析，研究表明在地下水的水解、溶蚀和动力作用下滑带土强度会显著降低。向云龙等［8］根据流体运动理论推求滑面底部裂隙径流对平推式滑坡产生的拖曳力，并修正了滑坡抗滑稳定性与后缘裂隙临界水深的关系。同时，在平推式滑坡运动量化方面，唐然［9］、李嘉雨［10］等在考虑后缘裂隙以及滑带中水的联合作用下，通过数学模型计算、数值模拟等方法，推导出平推式滑坡运动距离的计算公式。以上学者对平推式滑坡的成因机制，运动过程以及滑面的物质组成、水动力条件进行了深入研究，补充了滑坡启动中滑面的动态变化以及对滑体的力学影响。

在平推式滑坡的长期研究中，对成因机制的认识基本达成共识，认为滑坡竖向裂隙以及水平裂隙中的水在滑坡启动中起到关键作用，在计算过程中，将水平裂隙中的浮托力分布与竖向裂隙中的水力分布均看作三角形分布。但在众多平推式滑坡的物理模拟实验中，实测的水平裂隙的水力分布并不符合三角形分布，而是呈现下降速率逐渐增大的曲线。本文针对平推式滑坡的滑移面的水力分布规律，自主研制试验设备并进行水力测试试验，测量水的压力，总结滑动面水力分布规律，以期对滑坡的稳定性分析评价和治理方案提供参考。

1 平推式滑坡地质模型

根据平推式滑坡成因机制中水力启动模式，暴雨条件下后缘竖向裂隙水位逐渐升高并高于临界水位。在裂隙水的水平推力和滑移面水的浮托力联合作用下，滑坡下滑力大于抗滑力，滑坡失稳向前推出。竖向裂隙中的水压可视为静水压力，与水深有关；而滑移面中水存在渗流通道，并且水流运动过程中还存在阻力作用。本次研究选取成都市狮子山滑坡为地质模型进行水力测试试验，探索平推式滑坡滑移面的水力分布规律，分析水力启动机理。

1.1 滑坡概况

2013年8月8日06：00，成都市新津区永商镇狮子山发生小型岩质滑坡。滑坡位于斜坡中部，平面形态呈“箕”型，滑坡长约140 m，宽150～200 m、厚度3～15 m、平均厚度4 m、总方量约7.5万m3。滑坡发生在雨季，8月7日当日降雨量为108 mm。滑坡后缘形成巨大拉陷槽，滑坡整体向前位移约20 m。滑坡摧毁房屋4户，无人员伤亡。

1.2 滑坡基本特征

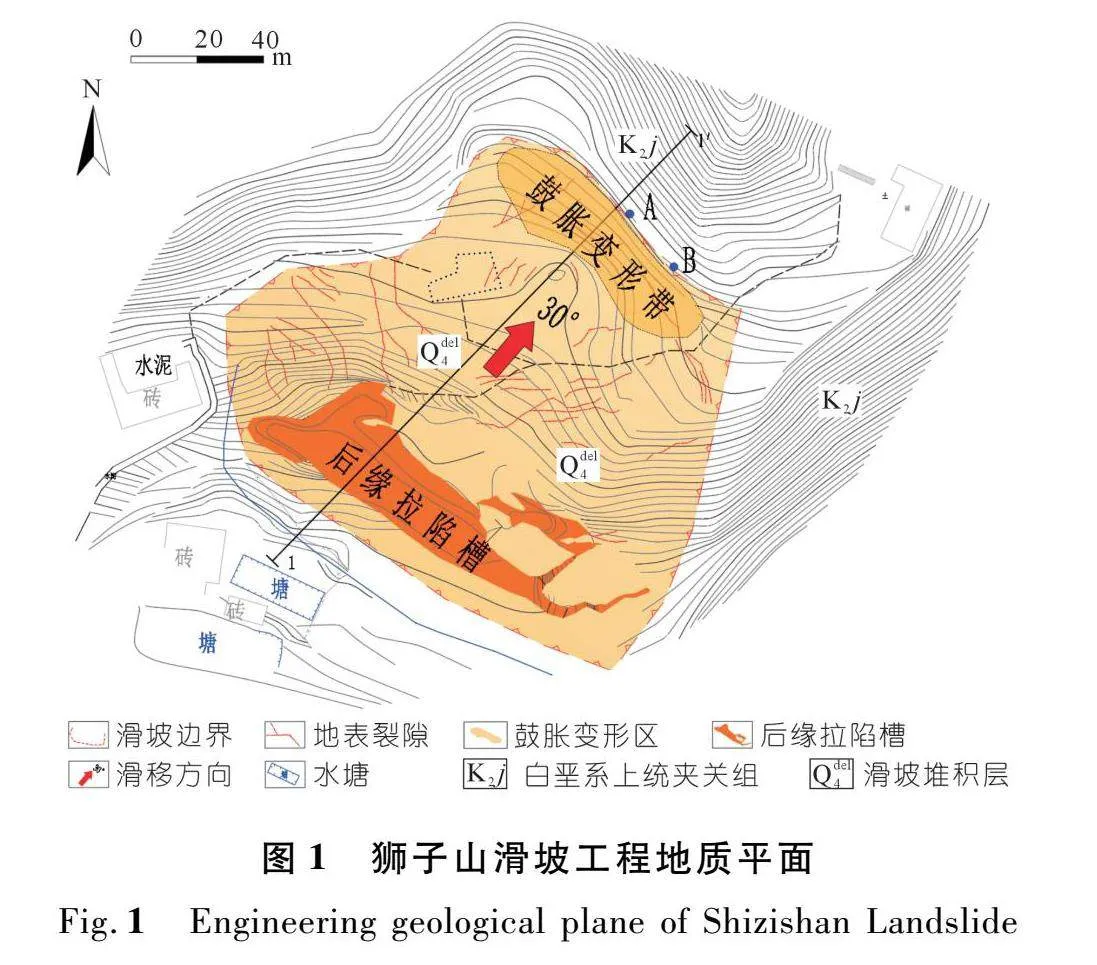
滑坡所处地质构造部位为熊坡背斜东北缘核部。地层岩性为白垩系上统夹关组（K2j）的厚层砂岩夹薄层泥岩。原始坡体浅表层为2～3 m厚的残坡积层与耕植土，其下为砂岩夹页的基岩，基岩岩层总体产状为30°～40°∠3°～6°（图1～2），走向与所在斜坡走向基本一致，基岩发育有NE向和NW向两组节理。

据气象资料显示，2013年8月4～8日，滑坡所在区域累计降雨量达194.7 mm，其中8月7日单日降雨量达108 mm。现场调查走访发现，在20世纪斜坡已出现漏水现象；受“5·12”汶川地震影响，斜坡发育有一条长拉裂缝，此后，暴雨条件下裂隙会发生不同程度的扩展。滑坡前缘存在两处地下水出露点，A点呈渗流状，B点呈股状流出。

1.3 变形破坏特征

滑坡运动过程中同时存在平移与右旋特征。总体滑动方向为NE30°，依据变形特征和变形程度将滑坡分为3个区：西侧剪切破坏区，拉陷槽拉张时，对周围岩土体进行拉张和剪切，导致西北侧形成两个次生滑坡，地表形成大量的剪切裂缝，呈羽状分布；中部平推前进区，有多条张拉裂缝，滑体推挤至前缘产生鼓丘；东侧微弱变形区，存在少量表生裂缝。

滑坡区变形破坏迹象明显，边界清晰：滑坡后缘发育有拉陷槽，平面形态为三角形，东侧收窄闭合，西侧拉开，最宽处约23 m（图3），长约130 m，底部高程一致，深约15 m；后缘岩壁陡立，岩石完整表面平直，滑坡体一侧岩石破碎，槽内填充崩落的碎石；东侧边界为一条北东-南西向张剪裂缝，长约100 m；西侧边界为西北侧陡坎；滑坡于前缘陡缓交界处剪出，剪出口处有两处地下水出露点。

2 平推式滑坡水力分布规律试验

范宣梅等［4］ 在采用物理模型试验对平推式滑坡成因机制研究中测量了滑移面的水压力。李伟［11-14］、赵权利［15］和涂园［16］等根据滑移面水的连续性原理，建立数学模型，并进行数学求解和敏感性研究，得到理论条件下承压水的分布规律。在前人计算过程中，为方便计算，常常忽略层间摩擦力以及水的黏滞力，采用水压力三角形分布形式，但这与现实情况不符。本次研究进行水力测试试验测得承压水的分布规律，以为实际案例中斜坡的稳定性评价和治理方案提供参考。

2.1 地质原型

以新津区狮子山滑坡为地质原型，建立地质概化模型（图4），开展典型平推式滑坡水力分布规律及启动机理研S/39LD9P3CR++fSoUvfGfQ==究。其中，AB段为竖直裂隙，地表水可沿此裂隙快速入渗，排水不畅时，可形成具有一定高度的水体。BC段为砂岩与泥岩边界处的结构劣化岩层，其中存在渗流通道。与完整岩石渗透性相比，其可视作透水层，上下岩石为不透水层。平推式滑坡的启动和制动，主要与后缘裂隙中水头高度相关。当AB段中水头高度到达临界高度时，滑坡启动；水位低于制动高度时，滑坡制动。BC段滑移面的承压水会对滑体底部产生向上的浮托力。BC段的水压力分布规律会影响最终的稳定性评价结果。前人研究中，承压水层（BC段）的水压力计算多采取三角形分布模式。

2.2 试验设备及方案

充分参考狮子山滑坡水力结构模型，水力测试试验设备为自行研制的“水力分布测试装置”（图5）。该仪器由动力装置、承压装置、测压装置3部分组成。动力装置对应模型AB段中水体对承压水层的水压力；承压装置对应BC段承压水层的3层层状结构；测压装置对承压水层各测点的水压大小进行测量。

动力装置由水头压力提供动力，主体为高度可调节的溢水槽，试验时外接水源至动力装置的溢水槽中，多余水流通过溢水管排走，稳定高度水面通过进水管与承压装置一端相连，为整个水力试验设备提供稳定压力。

承压装置由两层15 cm×30 cm的有机玻璃板组成。上层有机玻璃板完整，用于观察层间水流和填充颗粒的运移情况；下层玻璃板中部设有一排监测孔（图6），间距5 cm，共6个，与测压装置通过水管相连。两层有机玻璃板层间有间隙层，为水流通道，间隙层宽度可调，可填充不同物质，对应平推式滑坡底滑面的层状结构，两侧使用胶带封闭。后缘为进水口，通过水管与动力装置相连。前缘为出水口，可根据试验方案进行堵塞。

测压装置是测量监测孔水压所能支撑的水柱高度。主体由6支液位计组成，液位计底端与承压装置下层监测孔对应连接，液位计零点与下层玻璃板高度相平，上端与大气相通。液位计内水柱高度表示下层玻璃板该监测孔的水压大小。

试验时，外接水源使溢水槽中的水位高度稳定，水头压力将通过管道作用于承压装置中。承压装置中间隙层由水充满，待液位计水位高度稳定时进行读数，记录（图7）。

水力测试试验是以狮子山滑坡水力结构概化模型为理论基础，设立不同试验条件，获得层间水力分布状态，建立水力分布规律与层状结构之间的关系。在水力测试试验共设计2组试验，分别为前缘堵塞组、前缘贯通层间组。两组水头高度均为400 mm，设置倾角α=0°，2°，4°，6°，8°，10°，15°，对应不同倾角下的水力分布状态。试验时，前缘堵塞状态使用丁基胶带封闭前端出水口，层状结构倾角的调节时固定后端，调整前端高度，改变倾角。

2.3 水头高度分布规律

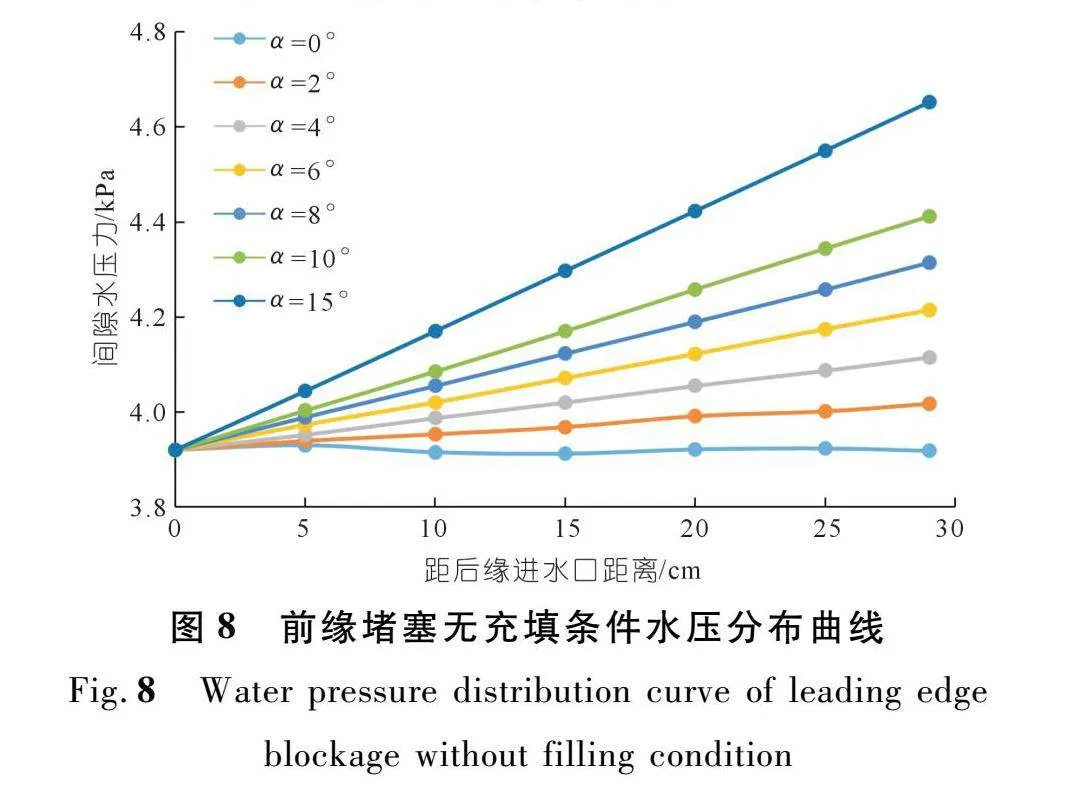
在前缘堵塞情况下，当底面水平时，各测点水头均等于后缘水头高度；底面倾角增大，前端高度降低，相对水头增加，越前缘间隙水压力越大（图8）。

在前缘贯通情况下，底面倾角增大过程中水位变化有以下特征：① 距后缘进水口越远，水头高度越低。② 底面倾角增大，距后缘进水口13 cm内水头高度升高，13 cm外水头高度降低（图9）。

2.4 结果分析

通过水力测试试验，可以观察到滑面的水力分布状态以及出水力分布与滑面倾角的定量关系。试验中，前缘堵塞条件下，水力分布与静水压力相同，即滑体底面所受压力为该点到自由水面的水柱高度。

前缘无堵塞情况下，承压水结构中出现两个自由水面（后缘水面和前缘出水口），即此点对滑体底面的水压力为0。后缘到前缘的水力下降速率并非为此前研究中假设为定值，即斜直线下降。试验中得出水力下降速率为先增大后减小，水力分布呈现为曲线。

3 讨 论

3.1 承压水水力分布规律

前人曾使用流体力学中连续介质力学方程等方法对平推式滑坡的启动临界水位、滑行距离进行计算。计算过程中，往往需简化滑移面上水压的分布形式。然而，滑移面的承压水水压研究中，滑带土和滑体物理力学参数、水体的黏滞性、孔隙的贯通情况以及光滑度等指标都会对水的水压情况产生影响。

针对平推式滑坡中底滑面的水力分布特征，以相似结构对间隙水压力进行测量，获得距离与水压的关系曲线（图10），通过多项式函数进行拟合，建立间隙水压力与位置的数学关系如式（1）所示。

y=-4.8108x4+11.315x3-7.4862x2-0.0185x+1

（1）

式中：y为间隙水压力比（某点的水压与后缘总水头的比值）；x为位置比（测点到后缘的距离与滑移面全长的比值）。

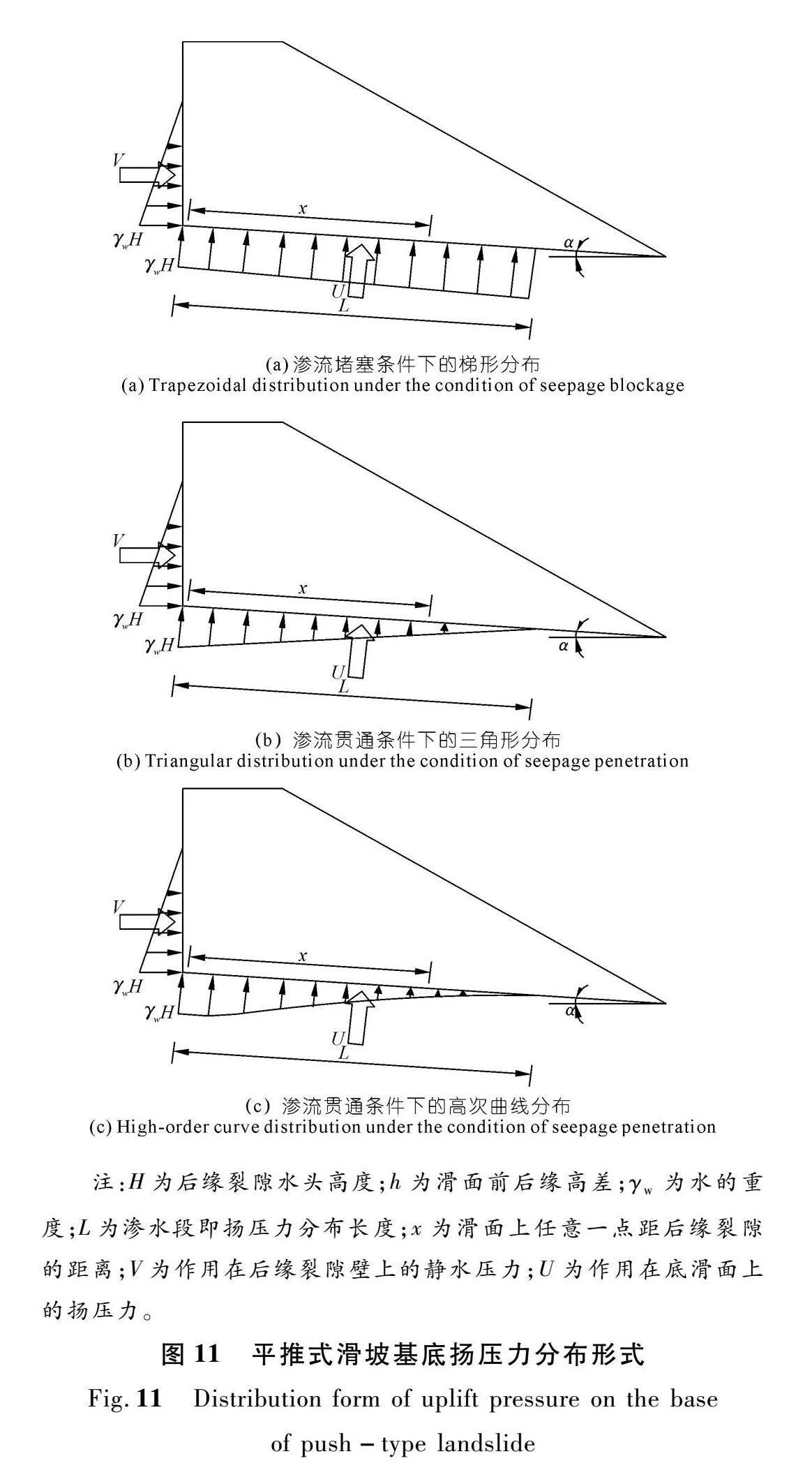
根据试验结果，前缘渗流条件会改变平推式滑坡中基底扬压力的分布形式。当底滑面渗流条件较差或滑坡前缘堵塞，便会使地下水流速度减慢或几乎静止，基底扬压力便会呈现梯形分布形态（图11（a））。其扬压力为

U1=γwHL+12γwL2sinα

（2）

当底滑面渗流条件较好时，地下水向坡表渗出，基底扬压力分布形式为提出的三角形分布［17］（图11（b））。其基底扬压力为

U2=0.5γwHL

（3）

在渗流贯通条件下，根据测试试验得出的基底扬压力为高次曲线分布（图12（c）），扬压力总值由式（1）积分得：

U3=0.36194γwHL

（4）

对比式（2）～（4）可知，U1 ＞ U2 ＞ U3，即后缘水头与渗水长度均相同时，扬压力大小依次为梯形分布＞三角形分布＞高次曲线分布。高次曲线分布要比三角形分布低27.6%。故采用三角形分布形式的扬压力对平推式滑坡进行稳定性评价时偏保守。三角形分布是将平推式滑坡的地画面视为光滑表面前提提出的，非线性的高次曲线分布形式是基于试验结果进行拟合获得，更能反映实际情况。

综上所述，滑坡底滑面的水压力由后缘裂隙中的潜水提供，潜水水位越高，底滑面后缘水压越大。当底滑面渗流条件较差或滑坡前缘堵塞时，地下水流速度减慢或几乎静止，水压力呈现梯形分布；当渗流条件较好时，水压力呈现曲线分布，水压力在底滑面方向上呈曲线下降，自后缘至剪出口下降速率先增大后减小。底滑面倾角越大，下降速率变化越显著。

3.2 启动机理分析

滑坡稳定性评价方法众多，本文采用极限平衡法中的传递系数法进行狮子山滑坡的稳定性计算。在后缘水头作用下，平推式滑坡底滑面中的承压水是从后缘裂隙逐渐向前缘流动的，扬压力的作用范围是与渗流过程有关的。由于扬压力会减小抗滑力，后缘裂隙蓄水后，潜在滑面上的扬压力作用范围逐渐向前缘扩展，扬压力作用范围内的浮托滑体抗滑力减小，剩余下滑力增加，没有受到扬压力作用的滑体部分受到的推力逐渐增大。当扬压力作用范围之外的天然滑体剩余抗滑力与所受推力相等时，滑坡处于临滑状态，稳定性系数等于1。基于GB/T 38509-2020《滑坡防治设计规范》中的不平衡推力传递法，考虑基底承压水逐渐渗流、扬压力分布的渐进扩展的过程及其分布形式，提出适用于平推式滑坡的极限平衡计算方案（图12）。

平推式滑坡稳定性系数计算公式为

Fs=n-1i=1Ri∏nj=i+1Ψj+Rnn-1i=1Ti∏nj=i+1Ψj+Tn

（5）

Ri=（Wicosαi-Ui）tanφ+cLi

（6）

Ti=（Wi+Vi=1）sinαitanφ+cLi

（7）

式中：Fs为滑坡稳定性系数；Ri为第i条滑块抗滑力，kN/m；Ti为第i条滑块下滑力，kN/m；Ψj为第i-1条滑块对第i条滑块的的传递系数，平推式滑坡为直线型滑面，取值为1.0；Wi为第i条滑块重量，kN/m；Ui为第i条滑块所受基底扬压力，kN/m；Vi=1为第1条滑块所受后缘静水压力，kN/m；φ为滑面内摩擦角，处于扬压力作用范围内取饱和参数，反之取天然参数，（°）；c为滑面黏聚力，处于扬压力作用范围内取饱和参数，反之取天然参数，单位kPa。

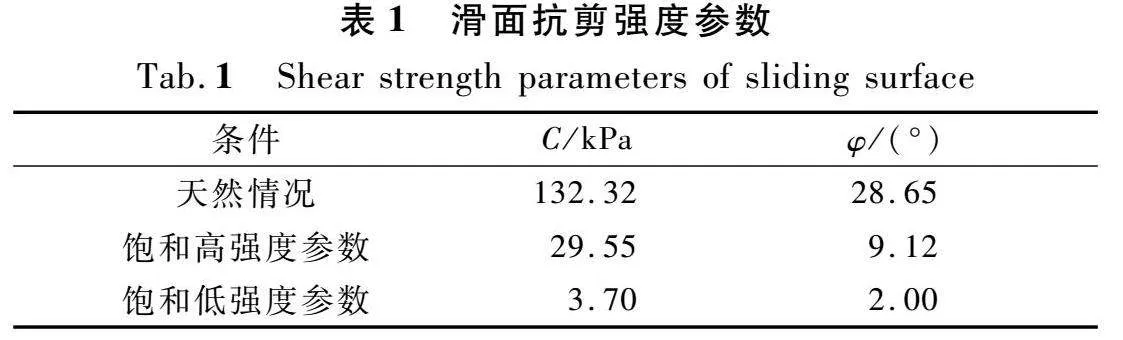
后缘拉陷槽完全充水情况下高度约为11.0 m。在最高水头情况下，基底扬压力采用高次曲线分布形式和传统三角形分布形式对饱和高、低强度参数分别进行计算稳定性计算（表1），其中，滑体的天然重度为21.2 kN/m3，饱和重度为23.6 kN/m3。

在饱和高强度参数下，两种分布形式稳定性系数均远大于1.0，考虑文章篇幅，本文仅展示饱和低强度参数的计算结果（表2）。

在饱和低强度参数情况下，扬压力为高次曲线分布时的临界长度高于三角分布，水压力分布长度差值在0.2 ～0.4 m之间，差距较小。无论何种扬压力分布形式，当扬压力分布扩展至100 m时，稳定性系数均接近于1.0或小于1.0。狮子山滑坡发生前后缘水头可能的最大高度为11 m，说明扬压力分布长度需超过100 m时，狮子山才会有失稳的可能。

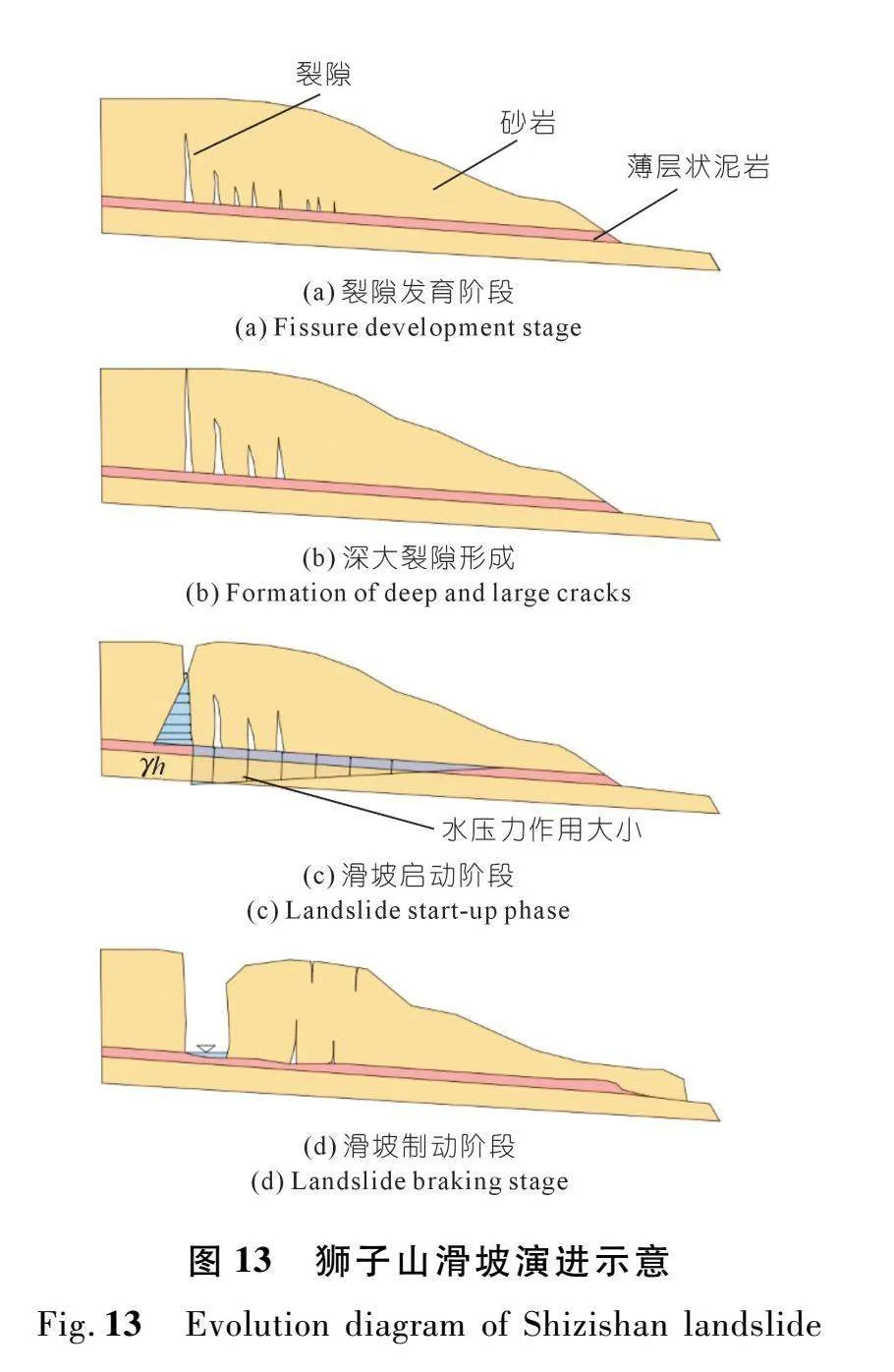
在滑坡地质条件、诱发因素和历史变形破坏特征等基础上，结合滑坡水力分布规律测试试验，综合分析狮子山滑坡的变形破坏过程可以概化为4个阶段（图13）：

（1） 裂隙发育阶段（图13（a））。斜坡倾向与岩层倾向一致，且倾角缓于坡向，坡体结构为厚层状砂岩夹薄层泥岩。斜坡在自身重力作用下有滑动的趋势。泥岩层相对于砂岩的力学性质而言，抵抗地下水软化能力较弱，在地质演化中，更易风化成泥质软弱夹层成为影响斜坡稳定性的关键层面。风化后的泥岩层强度不断降低，在滑体下滑力作用下发生塑性流动，滑体中产生自滑移面向上扩展的张拉裂隙。

（2）深大裂隙形成（图13（b））。2008年5月12日，在汶川地震水平加速度的作用下，块体间产生剧烈错动，部分裂缝裂隙扩展成深大裂隙，同时局部微张裂隙在上部位移下闭合。深大裂隙的形成为坡面水流进入坡体提供条件。坡体内部的渗透速度往往小于水面抬升速度，裂隙中常有积水赋存。竖向裂隙中的水在坡体中有两方面作用：① 其静水压力对坡体产生向外的推力，加快泥岩层的机械破碎，增大泥岩层的孔隙；② 加快泥岩层的软化，进一步降低滑动面抗剪强度。

（3） 滑坡启动阶段（图13（c））。暴雨情况下，单位时间内后缘裂隙排水量低于降雨量，在裂隙内形成一定高度的水头。水头的静水压力作用于滑体，并通过滑移面中的孔隙传递到滑块底部。滑坡体受裂隙中水提供向坡外的推力（γh）和滑面中水向上的浮托力。水头增大，水平推力增大；同时，斜坡底部渗流长度增加，扬压力逐渐增大，斜坡稳定性逐渐降低。在后缘裂隙水面上升至临界高度（11 m）时，滑坡失稳，向前开始滑动。

（4） 滑坡制动阶段（图13（d））。滑体整体向前部位移，拉陷槽宽度变大，裂隙网络进一步扩大、连通，拉陷槽中水面高度下降。水平推力低于抗滑力，滑坡制动。

薄层状泥岩的软化、变形是滑坡启动的根本原因［18-19］。软化岩层失去自身结构直接导致坡体发生蠕变，产生竖向拉裂缝。两次地震也极大加速了裂缝发育。滑坡启动的直接原因是：暴雨情况下，后缘裂隙中水位上升，后缘静水压力和层间水压力上升。滑体在底滑面扬压力和后缘裂隙中高水压下的水平推力联合作用下，滑坡抗滑力小于下滑力时滑坡启动。

4 结 论

以成都市狮子山滑坡为例，分析平推式滑坡的成因机制、变形特征，并采用试验测试方法对平推式滑坡变形破坏中的水力影响进行试验与量化分析，得出以下结论：

（1） 平推式滑坡多形成于近水平红层（倾角小于10°）。滑坡变形过程中为整体向外推出，滑体整体多能保证良好的完整性，后缘拉陷槽显著，坡表变化不大，变形破坏相对较小。

（2） 底滑面渗流条件较差或滑坡前缘堵塞条件下，水压力分布呈现梯形分布；流通条件下，水压力在底滑面方向上呈曲线下降，自后缘至剪出口下降速率先增大后减小，底滑面倾角越增大，下降速率变化越显著。

（3） 在滑移面渗流通道贯通情况下，高次曲线分布比经典的三角形分布关系曲线条件下提供的浮托力传统计算中的少27.6%。采用三角形分布形式的扬压力对平推式滑坡进行稳定性评价时偏保守。非线性的高次曲线分布形式通过试验所得，比三角形分布形式更能接近实际情况。

（4） 平推式滑坡启动机理可概括为裂隙发育—深大裂隙形成—滑坡启动—减速制动4个阶段。在斜坡演变中，泥岩层向坡外塑性流变，使得坡体中产生自下而上发育的竖向裂缝。暴雨条件下，竖向裂隙中的水压力与滑移面的地下水浮托力联合作用使滑坡滑出。后缘裂隙水位降低，水平推力下降，滑体制动。

参考文献：

［1］ 张倬元，王仕天，王兰生，等.工程地质分析原理［M］.4版.北京：地质出版社，2016.

［2］ 王兰生，李曰国，詹铮.1981年暴雨期四川盆地区岩质滑坡的发育特征［J］.大自然探索，1982（1）：44-51.

［3］ 殷坤龙，简文星，周春梅，等.万州区近水平地层滑坡和堆积体成因机制与防治工程研究［R］.武汉：中国地质大学，2005.

［4］ 范宣梅，许强，张倬元，等.平推式滑坡成因机制研究［J］.岩石力学与工程学报，2008（增2）：3753-3759.

［5］ 郭晓光，黄润秋，邓辉，等.平推式滑坡多级拉陷槽形成过程及成因机理分析［J］.工程地质学报，2013，21（5）：770-778.

［6］ 张明，胡瑞林，殷跃平，等.川东缓倾红层中降雨诱发型滑坡机制研究［J］.岩石力学与工程学报，2014，33（增2）：3783-3790.

［7］ 蒋宇，赵宇.基于特征矿物的红层滑坡形成机理分析［J］.人民长江，2021，52（6）：82-87.

［8］ 向云龙，符文熹，周洪福.考虑裂隙水流拖曳力效应的平推式滑坡稳定性［J］.岩土工程学报，2018，40（增2）：173-177.

［9］ 唐然，许强，吴斌，等.平推式滑坡运动距离计算模型［J］.岩土力学，2018，39（3）：1009-1019，1070.

［10］李嘉雨，王崇艮，毛邦燕，等.基于滑距计算与危险性评价的某平推式滑坡防治对策研究［J］.长江科学院院报，2021，38（4）：63-69，80.

［11］李伟，吴礼舟，肖蓉.平推式滑坡中承压水的敏感性研究［J］.工程地质学报，2017，25（2）：480-487.

［12］李伟，肖蓉，吴礼舟.岩质边坡中结构面上水压分布假设的改进研究［J］.岩石力学与工程学报，2017，36（3）：599-608.

［13］李伟，许强，吴礼舟，等.平推式滑坡中底滑面承压水渗流形式对其稳定性的影响［J］.岩土力学，2018，39（4）：1401-1410.

［14］李伟，詹良通，王康.水力作用下平面滑动岩质边坡极限倾角解析计算［J］.岩石力学与工程学报，2018，37（4）：876-886.

［15］赵权利，孙红月，王智磊，等.承压水对平推式滑坡的作用分析［J］.岩石力学与工程学报，2012，32（4）：762-769.

［16］涂园.平推式滑坡承压水模型研究［J］.岩石力学与工程学报，2018，37（9）：2110-2119.

［17］张家旭，易庆林，邓茂林，等.三峡库区三门洞滑坡复活机理及韧性变形研究［J］.人民长江，2024，55（4）：160-168.

［18］杨连伟.金沙江白格滑坡失稳机理及影响因素分析［J］.人民长江，2023，54（1）：119-125，176.

［19］雷菁，雷洁.库水位涨落对某库岸堆积体滑坡稳定性研究［J］.水利水电快报，2018，39（4）：25-28.

（编辑：刘 媛）

Study on hydraulic distribution law and start-up mechanism of typical translational landslide

CHEN Lixin1，WANG Zhenyu2，JI Feng1，GUO Pengyu1

（1.State Key Laboratory of Geohazard Prevention and Geo-environment Protection，Chengdu University of Technology，Chengdu 610059，China； 2.Sichuan Vocational and Technical College of Communications，Chengdu 611130，China）

Abstract：

Translational landslides occur in nearly horizontal strata and groundwater plays a crucial role in their initiation and subsequent movement.This study aimed to explore the correlation between the hydraulic distribution on the shear plane and the initiation of the landslides.Using the Shizishan Landslide in Chengdu City as a geotechnical model，a bespoke apparatus was developed for hydraulic testing.The experiment measured the hydraulic pressure at various points along the base sliding plane of nearly horizontal angles from 0° to 10°，under two penetration conditions，to investigate the distribution pattern of hydrostatic pressure.The outcomes revealed that：① Under poor permeability on a bottom sliding plane or the landslide's front was obstructed，the hydraulic pressure exhibited a trapezoidal distribution.Conversely，under free-flow conditions，the hydraulic pressure decreased in a curvilinear pattern along the basal sliding plane，with the decreasing rate first ascending and then slowing from the rear to the front.The steeper the angle of the basal sliding plane，the more notable the decreasing rate change.② Hydraulic uplift pressure in interlayer fractures was found to be around 27.6% less than the pressures calculated using traditional triangular distribution models.③ The softening and deformation of thin layers of mudstone were the root causes of landslide initiation.Specifically，the trigger for landslide initiation was the result of intense rainfall causing uplift pressure on the bottom and high-pressure water within the rear-edge fractures，which worked in tandem to thrust the landslide mass.These findings can offer an important reference for the stability analysis，assessment，and remediation plans for translational landslides.

Key words：

translational landslide； hydraulic distribution； confined water； pore water pressure； initiation mechanism； engineering geology