多重不确定性下水风光多能互补长期优化调度方法

摘要：如何应对水风光多重不确定性及其导致的高维优化求解难题是流域水风光多能互补长期调度面临的关键挑战。为此，提出基于马尔科夫链和Copula函数的水风光联合场景生成方法，并通过同步回代缩减法进行场景削减，量化表征水风光多重不确定性；以此为输入，构建流域水风光多能互补长期两阶段随机优化调度模型，并通过Benders分解算法和凸化线性化建模技术实现高维非线性优化问题的高效求解。最后以金沙江下游清洁能源基地为研究对象进行了仿真验证。通过对比分析，证明了所提方法能够有效提升长期调度方案对水风光不确定环境的适应性，提高了多能互补综合效益。在样本外检验中，所提方法比传统方法的发电量增加了0.552亿kWh，弃水量减少了1.694亿m3，表现得更具可靠性。

关 键 词：水风光多能互补； 长期调度； 两阶段随机优化； Benders分解

中图法分类号： TV697.1

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2024.09.004

0 引 言

流域水风光一体化是推动实现能源绿色转型和新能源高质量发展的重要路径［1-3］。由于径流和风光发电能力在长期尺度上表现出很强的随机性［4-6］，再叠加梯级水电站复杂水力、电力联系，其明显的非线性运行特征以及防洪、生态等复杂需求［7-8］，导致流域水风光一体化长期调度面临建模和求解两大难题。建模方面难点主要体现为如何生成高效水风光耦合场景并将其合理纳入调度模型框架，充分提升调度方案对不确定环境的适应性；求解方面难点则体现在多维场景集、梯级水电站复杂运行特性导致的大规模非线性优化求解。

长期多能互补优化调度能够有效促进新能源消纳［9-10］，探索长期优化调度策略对多能互补系统至关重要。因此，围绕多能互补长期调度建模和求解问题，学者们开展了广泛的研究。

在多能互补长期调度建模方面，闻昕等［11］提出了一种基于余留期效益函数的随机优化调度方法，用以指导水光互补系统的长期调度运行。Cao等［12］通过场景树方法生成长期尺度场景集，并将其输入到随机规划模型中，有效提高了系统的长期运行性能。Zhang等［13］开发了一种混合模型估计水风资源的联合概率分布，并生成大量场景纳入调度模型中，提高了互补系统的经济效益。Hu等［14］提出了大规模水风光系统优化调度混合整数规划模型，以提升系统运行效率。在多能互补长期调度求解方面，赵志鹏等［15］采用动态规划、离散微分动态规划和逐步优化结合算法高效求解多目标调度模型。Li等［16］基于随机动态规划求解考虑径流和光伏发电量不确定性的长期随机优化，实现发电量和发电保证率最大化。Yang等［17］基于隐随机优化调度方法，制定水光互补系统的中长期优化调度规则，有效提高了系统效益。上述文献针对多能互补长期调度建模与求解进行了诸多有益探索，然而如何准确量化多能互补系统水风光不确定性，生成水风光耦合场景，并有效解决在其纳入优化调度模型后的求解问题依然需要进一步研究。

因此，本文提出一种考虑多重不确定性的流域水风光多能互补长期优化调度方法。首先提出基于马尔科夫链和Copula函数的水风光联合场景生成方法，并基于同步回代缩减法对生成的大量径流、风光出力场景集进行缩减获得水风光典型场景；其次，建立考虑计划发电量与实际发电量偏差的两阶段随机优化调度模型，然后依据Benders分解算法将模型分为主问题和子问题，通过对其循环迭代求解所提出的两阶段随机优化模型；最后以金沙江下游清洁能源基地为例进行对比仿真，验证了本文所提方法能够有效指导多能互补系统的调度运行。

1 数学模型

1.1 目标函数

发电量最大是传统长期随机优化调度模型最常见的目标函数。本文在此基础上考虑计划发电量与实际发电量的偏差构建两阶段随机优化调度模型。第一阶段对多能互补系统各水电站的水位过程进行决策；第二阶段在典型场景下模拟水库运行，其目标是选择最优的水位，令多能互补系统总发电量最大，具体目标函数如下：

maxE=Nn=1

Tt=1

（PHn，t+PWindn，t+PPVn，t）Δt-

Nn=1Tt=1Ww=1pwen，t，w

（1）

式中：n，N分别为电站编号和电站数量；t，T分别为时段编号和调度时段数；PHn，t、PWindn，t、PPVn，t分别为第n个水电站在时段t的出力及其接入的风电站与光伏电站的出力，MW；Δt为t时段的时间长度；w，W分别为场景编号和场景数；pw表示第w组场景的概率；en，t，w表示第w场景时第n个水电站及其接入的风光电站在时段t的计划总发电量与实际总发电量的偏差，MW·h，如式（2）所示：

en，t，w=（PHn，t+PWindn，t+PPVn，t）Δt-

（PHf，n，t，w+PWindf，n，t，w+PPVf，n，t，w）Δt

（2）

式中：PHf，n，t，w、PWindf，n，t，w、PPVf，n，t，w分别表示第w场景时第n个水电站在时段t的出力及其接入的风电站与光伏电站的出力。

1.2 约束条件

（1） 水量平衡约束。

vn，t+1=vn，t+3600Δt×（qinputn，t-qoutputn，t）

qinputn，t=qoutputn-1，t+qrangen，t

qoutputn，t=qpowern，t+qspillagen，t

（3）

式中：vn，t表示第n个水电站在t时刻的库容，m3；qinputn，t表示第n个水电站在时段t的入库流量，m3/s；qoutputn，t表示第n个水电站在时段t的出库流量，m3/s；Δt表示t时段的小时数；qrangen，t表示第n个水电站在时段t的区间流量，m3/s；qpowern，t表示第n个水电站在时段t的发电流量，m3/s；qspillagen，t表示第n个水电站在时段t的弃水流量，m3/s。

（2） 水位约束。

Zn，t≤zn，t≤Z—n，t

（4）

式中：zn，t表示第n个水电站在t时刻的水位，m；

Z—n，t和Zn，t分别为第n个水电站在t时刻的水位上、下限，m。

（3） 发电流量约束。

Qpowern，t≤qpowern，t≤Q—powern，t

（5）

式中：Q—powern，t和Qpowern，t分别为第n个水电站在t时刻的发电流量上、下限，m3/s。

（4） 出库流量约束。

Qoutputn，t≤qoutputn，t≤Q—outputn，t

（6）

式中：Q—outputn，t和Qoutputn，t分别为第n个水电站在t时刻的出库流量上、下限，m3/s。

（5） 出力限制约束。

PHn≤PHn，t≤P—Hn

（7）

式中：P—Hn和PHn分别为第n个水电站的出力上、下限，MW。

（6） 通道能力限制约束。

PHn，t+PWindn，t+PPVn，t≤P—Ln

（8）

式中：P—Ln为第n个水电站的现有通道能力，MW。

（7） 水位-库容关系。

zn，t=fzvn（vn，t）

（9）

式中：f zvn（·）为第n个水电站的水位-库容关系函数。

（8） 水电站出力函数。

PHn，t=3.6×qpowern，trn，t

（10）

式中：rn为第n个水电站在t时刻的耗水率，m3/（kW·h）。

（9） 始末水位控制。

zn，1=zstartn

zn，T+1=zendn

（11）

式中：zstartn和zendn分别为第n个水电站调度期初水位和调度期末的控制水位，m。

（10） 实际水位与计划水位偏差。

|zn，t-zf，n，t，w|≤δn

（12）

式中：zf，n，t，w为第w场景时第n个水电站在时段t的水位，m；δn为第n个水电站允许的实际水位与计划水位的偏差。

由于本文所提模型为两阶段随机优化模型，对第二阶段目标求解时同样需要满足约束（1）～（9）。

1.3 约束处理

（1） 水位-库容关系线性化。

一般情况下，水库库容是关于水位的非线性函数，因此需要线性化处理。

对于具有日调节以上调节性能的水电站，其死水位至正常高水位区间内水位-库容关系基本呈线性，可在该区间内对水库水位和库容进行线性回归分析来表示水位-库容关系函数［18］，如式（13）所示：

vn，t=αnzn，t+βn

（13）

式中：αn，βn为第n个水电站的水位-库容关系线性化参数。

（2） 绝对值约束线性化。

对于目标函数中存在的绝对值式（2），采取如下方式进行处理：

en，t，w≥（PHn，t+PWindn，t+PPVn，t）Δt-

（PHf，n，t，w+PWindf，n，t，w+PPVf，n，t，w）Δt

（14）

en，t，w≥（PHf，n，t，w+PWindf，n，t，w+PPVf，n，t，w）Δt-

（PHn，t+PWindn，t+PPVn，t）Δt

（15）

对式（10）中的实际水位与计划水位偏差约束，则可转换为

-δn≤zn，t-zf，n，t，w≤δn

（16）

2 求解方法

2.1 场景生成与削减

2.1.1 场景生成

本文提出的场景生成方法分为两步：第一步通过马尔科夫链模型捕捉水风光时序特性，并结合蒙特卡洛抽样生成考虑时间相关性的初始场景集；第二步基于C-vine Copula进一步生成水风光耦合场景集，流程如图1所示。

以径流为例阐述生成考虑时间相关性的初始场景集的详细步骤：

（1） 假设当前月份t的径流状态为θt，流量为ωt，生成一个服从均匀分布的随机数ε1t且ε1t∈［0，1］。

（2） 依据当前月份选定相应的累积状态转移矩阵Qh，其元素为qi，j=jδ=1pi，δ，其中pi，j为状态转移矩阵Ph中的元素，表达式为

pij=P（θt+1=jθt=i）=nij/（Nk=1nik）

（17）

式中：nij表示相继过程i→j的转移次数。

（3） 判断ε1t与对应矩阵第θt行元素的大小关系，从而确定下一月份风电出力的状态θt+1，为确定该月具体流量，再生成一个服从均匀分布的独立随机数ε2t∈［0，1］。设与状态θt+1相应的取值区间为［ω1，ωr］，则有ωt+1=ω1+ε2t（ωr-ω1）。

（4） 令t=1，重复步骤（1）～（4）直到t=12结束，即完成一个场景序列的生成。

（5） 循环上述步骤W次，即可得到包含W个场景的初始径流场景集SI，h（本文中W取300），初始风电、光伏出力场景集SI，w、Sl，s可按同样步骤生成。

基于第一步生成的多能互补系统初始场景集，结合C-vine Copula进一步抽样生成考虑时空相关性的水风光耦合场景集，具体步骤如下：

（1） 确定多能互补系统C藤结构，并选择藤结构每条边的最佳pair Copula函数，流程参考文献［19］，C-vine Copula联合概率分布表达方式如下：

f（x1，…，xn）=∏nk=1f（xk）∏n-1j=1∏n-ji=1cj，j+1|1，…，j-1

［F（xj|x1，…，xj-1），F（xj+i|x1，…，xj-1）］

（18）

式中：cj，j+1|1，…，j-1（·）为在已知x1，x2，…，xj-1的条件 下，变量xj和xj+i二者构成的Copula概率密度函数；F（xj|x1，…，xj-1）为在已知x1，x2，…，xj-1的条件下，变量xj的分布函数。

（2） 令均匀变量Z1∈［0，1］为某种资源初始场景集对应的累积概率，生成服从0-1均匀分布的随机数，定义为均匀变量Z2。

（3） 令U1，U2，U3为3组待求变量，第1组待求变量等于（2）中的第一组变量，即U1=Z1，Z1为变量U1的采样点。

（4） 由式（18），第2组待求变量U2可利用Z2=F（x2|x1）=C（U1，U2）/U1计算，Z2和U1均为已知量，由此将问题转化为一元线性方程求解问题，所得结果即为变量U2的抽样数据。

（5） 同理，由于Z2、Z3已被定义，可以由Z3=F（x3|x1，x2）=Cx3，x2|x1（F（x3|x1），Z2）/Z2得F（x3|x1），又F（x3|x1）=C（U1，U3）/U1，重复步骤（4）求得结果为U3的抽样数据。

（6） 对U1，U2，U3进行逆变换抽样，最终将上述所得的随机数样本转化为考虑时空相关性的水风光耦合场景集。

2.1.2 场景削减

采用同步回代缩减方法［20］对生成的大量场景进行缩减。具体步骤如下：

（1） 设置每个初始场景的概率为1/W。

（2） 计算每对场景之间的概率距离，并找到概率距离最小的场景，将其剔除。

（3） 将场景总数减少至W=W-1，并将被剔除场景的概率加到距离该场景最近的场景上，以确保剩余场景的概率总和为1。

（4） 如果剩余的场景总数W仍大于指定的保留场景个数，则返回步骤2，直到减少到指定的保留场景个数为止。

2.2 Benders分解法

随着场景数量的增加，本文模型的复杂度将呈指数级增长，直接求解将耗费大量的时间。Benders分解算法作为一种求解大规模混合整数线性优化问题（mixed integer linear programming，MILP）的迭代算法，通过划分复杂变量和易处理的变量，将模型分为主问题（master problem，MP）和子问题（subproblem，SP），并对主问题和子问题依次求解，从而使问题维数降低，提高模型求解效率。设置第一阶段决策变量y={zn，t，vn，t，qpowern，t，qspillagen，t，PHn，t}，第二阶段变量xw={zf，n，t，w，vf，n，t，w，qpowerf，n，t，w，qspillagef，n，t，w，PHf，n，t，w，en，t，w}，带有下标f、w表示第w个场景的实际值。

为了方便求解，将所提模型写成如下紧凑形式：

miny，{xw}-aTy+Ww=1bTxw

s.t.

Ay+k=0

By≥d

Fxw=g

Mxw-Iuw=0

Dxw≥f

Gxw+Jy-Ruw≥j

（19）

式中：A、B、F、M、I、D、G、J、R分别为模型中各个约束所对应的系数矩阵；a、b、k、d、g、f、j为常数列向量；uw代表第w个场景的不确定性变量；第1条约束代表第一阶段约束式（1）、（7）～（9）；第2条约束代表第一阶段约束式（2）～（6）；第3条约束代表第二阶段约束式（7）～（9）及n≠1时的第二阶段约束式（1）；第4条约束代表n=1时的第二阶段约束式（1）；第5条约束代

表第二阶段约束式（2）～（5）；第6条约束代表第二阶段约束式（6）及（14）～（16）。

对式（19）进行分解，得到第一阶段主问题MP，如式（20）所示和第二阶段子问题SP如式（21）所示。首先求解MP，得到下界LB；将MP解得的第一阶段变量y代入求解SP，得到上界UB，相应地向MP添加新的约束；交替求解MP与SP，判别其是否满足阈值，从而获得最优解，MP及SP具体形式如下：

MP

miny，{xw}-aTy+Ww=1θw

s.t.

θw≥bTxw

Ay+k=0

By≥d

Fxw=g

Mxw-Iuw=0

Dxw≥f

Gxw+Jy-Ruw≥j

（20）

SP

minxwbTxw

s.t.

Fxw=g → λ1

Mxw-Iuw=0 → λ2

Dxw≥f → λ3

Gxw+Jy-Ruw≥j → λ4

（21）

根据强对偶理论与式（21）中的对应关系，将SP转化为max形式：

maxλ1，w，λ2，w，λ3，w，λ4，wgTλ1，w+（Iuw）Tλ2，w+fTλ3，w+

（Ruw+j-Jy）Tλ4，w

s.t.

FTλ1，w+MTλ2，w+DTλ3，w+GTλ4，w≤b

λ1，w，λ2，w，λ3，w，λ4，w≥0

（22）

具体求解步骤为

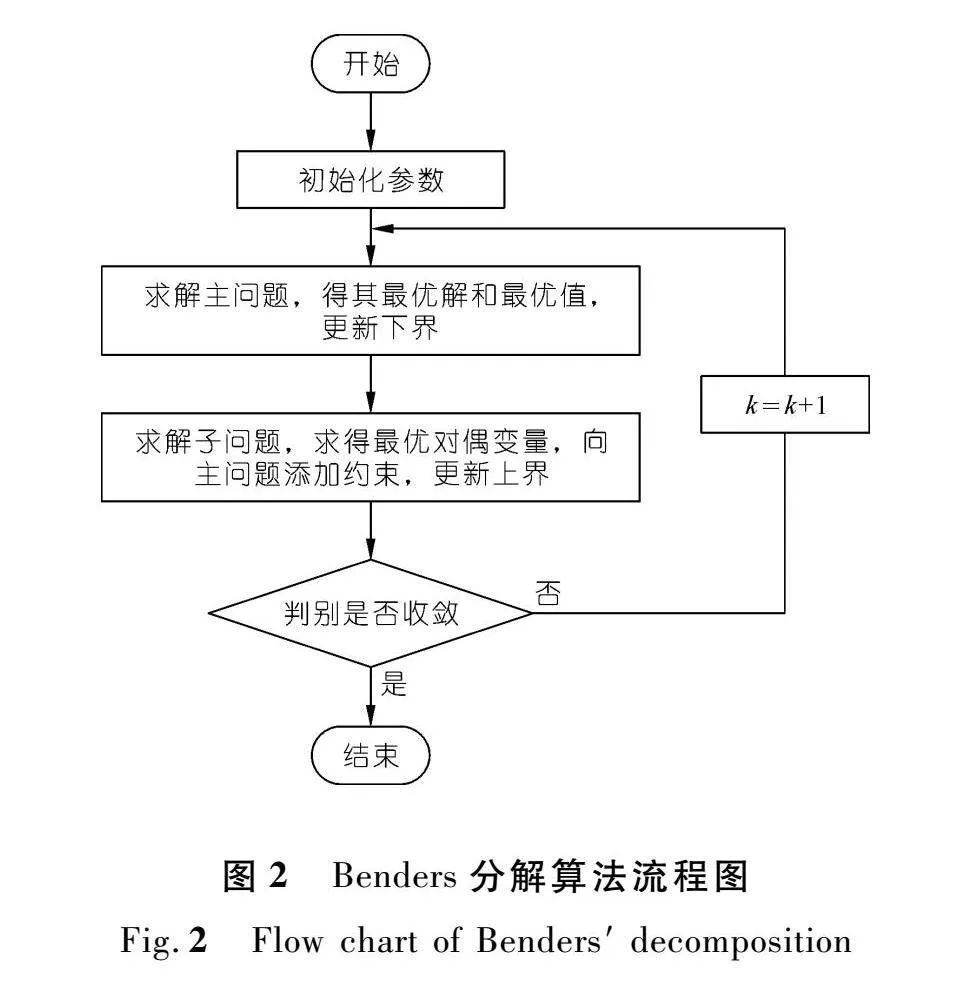
（1） 设置模型上界UB=+∞，下界LB=-∞，收敛阈值ε=0.000 01，迭代次数k=1。

（2） 求解主问题，得其最优解x*k和最优值E*k，更新下界LB=max{LB，E*k}。

（3） 对每组场景w∈W，代入x*k求解子问题，求得最优对偶变量λ*1，w，k，λ*2，w，k，λ*3，w，k，λ*4，w，k，向主问题添加最优割约束：

gTλ*1，w，k+（Iuw）Tλ*2，w，k+fTλ*3，w，k+

（Ruw+j-Jy）Tλ*4，w，k≤θw

（23）

并更新上界：

UB=max{UB，-aTy+Ww=1gTλ*1，w，k+（Iuw）Tλ*2，w，k+

fTλ*3，w，k+（Ruw+j-Jy）Tλ*4，w，k}

（24）

（4） 当（UB-LB）/|UB|≤ε，迭代结束。输出当前的x*k；否则，令k=k+1并返回（2）重新进行计算。求解流程图如图2所示。

3 实例分析

3.1 数据资料

以金沙江下游清洁能源基地作为实例研究对象。金沙江下游干热河谷地段由于地势及气候等因素的影响，风光资源丰富，且金沙江下游建有电站A、电站B、电站C、电站D四座巨型水电站，总装机容量达4 646万kW。水电站基本信息如表1所列。

本文获得水风光典型场景时使用的风电和光伏出力数据是基于参考文献［16］中描述的方法，利用欧洲中期天气预报中心（European Centre for Medium-Range Weather Forecasts，ECMWF）的ERA5再分析数据折算得出的。径流数据则是从电网公司获取的，数据采集步长为每月一次，时间范围为1990～2021年。

本文所提模型在Python环境下实现，调用Gurobi9.1求解。计算环境为 Intel（R） Core（TM） i7-1165G7 CPU @2.80GHz，16GB RAM。

3.2 结果分析

根据给定的径流及风光出力数据，应用2.1节提到的场景生成和缩减方法生成10组径流及风光出力典型场景量化多能互补系统的水风光不确定性，如图3所示。

3.2.1 收敛性分析

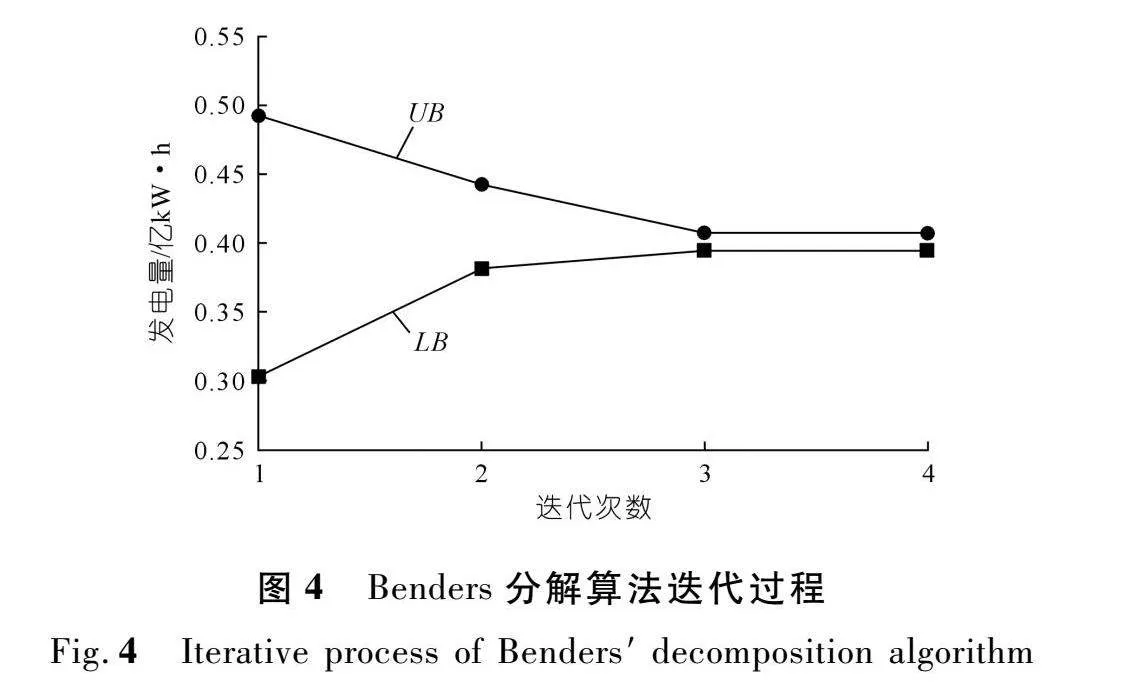
图4验证了Benders分解算法的收敛性，本文所提模型在迭代3次后完成收敛。主问题约束随着最优割数量的增加而更严格。由主问题计算得出的下界LB变大，水风光多能互补系统的调度方案变得越来越合理。同时，子问题通过最优割检验主问题所求得的调度方案的效果，并指出了优化方向。当上、下界满足收敛阈值时，最新的调度方案被认为是最优的，并终止Benders分解算法。

3.2.2 调度结果

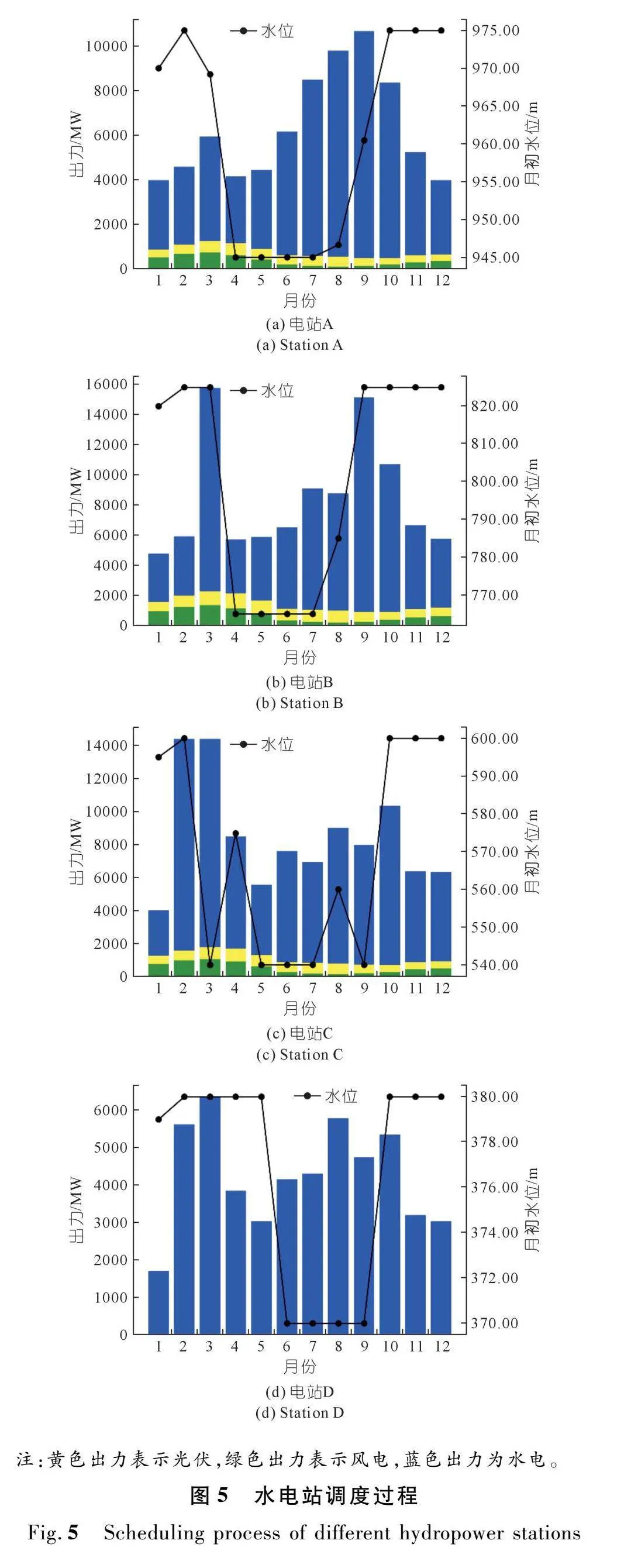
图5是本文所提调度方法的水风光多能互补系统出力及水位过程。电站D由于未接入风光电站，所以仅有水电出力。由图5可见：电站A出力在1～9月逐步上升，在达到峰值之后迅速下降；电站B在3月份出力最大，达到15 760.76 MW，主要得益于该月耗水率比相邻月份更大，增加其发电流量有利于获得更多的效益，并且由于风光发电能力具有季节性特征，该月接入电站B的风光出力最大；电站C和电站D总体都呈现先减小后增大的趋势，存在一定的月间波动。电站A的水位在4月降至死水位945.00 m，随后在7月开始上升，至10月达到正常高水位975.00 m，并维持至年底。电站B在初期水位略升后，4月降至死水位765.00 m，随后平稳运行至7月，之后水位逐渐升高至825.00 m的正常高水位，并保持至年底。电站C在3月降至死水位540.00 m后，尽管水位有所波动，但始终符合月间变幅限制，9月升至正常高水位600.00 m后保持稳定。电站D由于其正常高水位与死水位相差仅10.00 m，全年基本在这两个水位之间运行。

3.2.3 典型场景影响

本文进一步探究典型场景对本文所提方法的影响。分别设置典型场景数为5，10，20的调度方案为方案1（a）、（b）、（c）。比较本文所提方法在这3种方案下的性能。

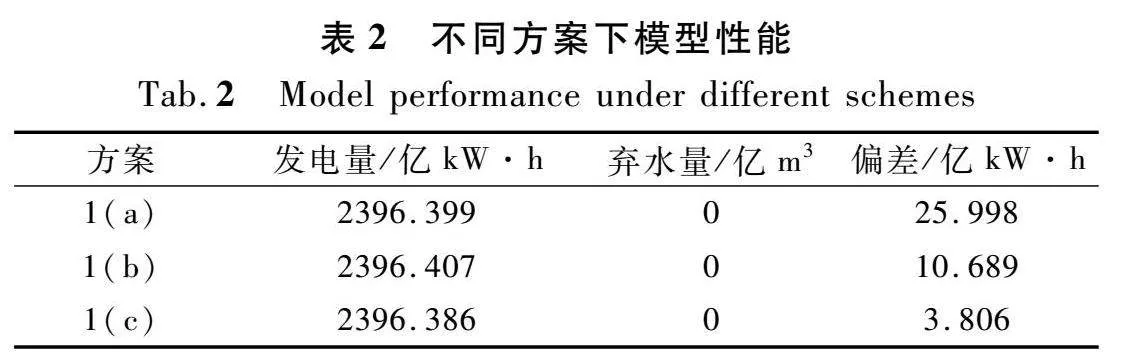
表2为方案1（a）、（b）、（c）的发电量、弃水量以及计划发电量和实际发电量的偏差变化。由表2可以看出，方案1（b）即当典型场景为10时，发电量最大，分别比方案1（a）和方案1（c）多0.008亿kW·h和0021亿kW·h。从弃水量指标来看，3种方案多能互补系统的弃水量都为0。随着典型场景数的增加，计划发电量和实际发电量的偏差逐渐减小。但事实上，由于场景数的增加，模型求解时间也会指数倍增长。

电站A中的水电站部分是金下梯级水电站的龙头电站，且由于其余3个水电站调节能力较强，因此不同的典型场景数对其水位影响不大。电站A的水电站在3种方案的水位过程变化如图6所示。3种方案的水位过程的差异主要体现在水位抬升状态的8、9月份。整体来看，方案1（b）的水位过程相对较低，可以使水量利用更加充分，有利于提升单位水量所产生的电量。

综上所述，选取典型场景数为10时，模型性能最好。

3.2.4 有效性分析

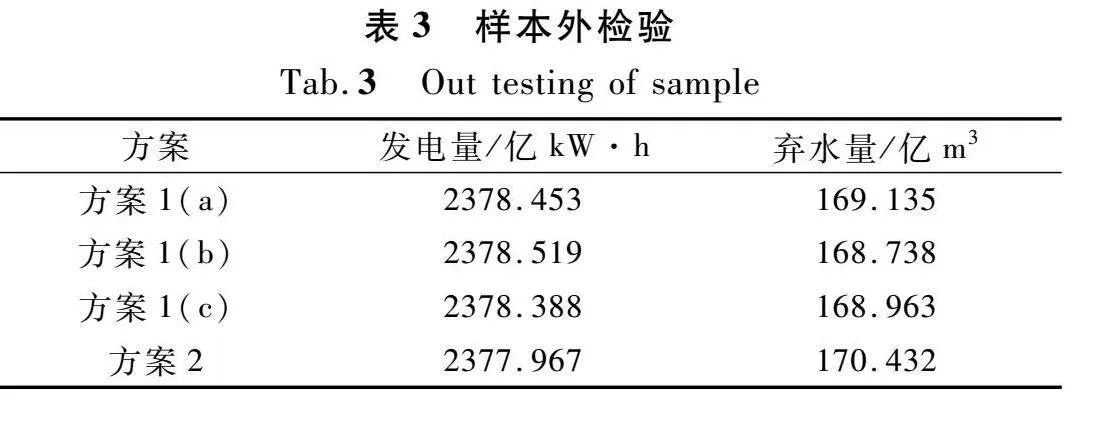
为验证本文所提方法的有效性，本文通过蒙特卡洛模拟生成1 000个场景进行样本外检验。将不考虑计划出力与实际出力偏差的确定性模型得出的调度方案确定为方案2。比较该方案与3.2.3节3种方案对应的的平均发电量及弃水量。

结果如表3所列，方案1（a）、（b）、（c）的平均发电量和弃水量明显优于方案2，即确定性模型得出的调度方案。其中方案1（b）由于取到了最佳典型场景数，所以在样本外检验中表现最优，其平均发电量为2 378.519亿kW·h，分别比方案1（a）、方案1（c）和方案2多了0.066亿，0.131亿，0552亿kWh。对于平均耗水率指标，方案1（b）的弃水量最少，为168.738亿m3，方案2的弃水量则达到了170.432亿m3。由此可见，本文所提模型相比确定性模型具有更好的效果，这是因为本文所提模型考虑了水风光资源的不确定性和计划发电量与实际发电量的偏差，所以表现为在样本外检验中效益更好，更具稳定性。

4 结 论

本文提出了一种考虑多重不确定性的流域水风光多能互补长期优化调度方法，并以金沙江下游梯级电站为例对模型进行了验证，研究结论如下：

（1） 本文提出用Benders分解算法来有效求解两阶段随机优化模型。该算法通过不断迭代，满足阈值，从而快速收敛。所得的调度方案能够在很好地保证多能互补系统发电效益的同时，对各水电站的水位过程进行合理调控。

（2） 探究了典型场景数对本文所提方法的影响。结果表明典型场景数为10时，所提模型发电量相对典型场景数为5和20时提高了0.008亿kW·h和0021亿kW·h，具有最优的综合性能。

（3） 本文所提模型由于考虑了水风光资源的不确定性和计划发电量与实际发电量的偏差，在样本外检验中表现更具稳定性。与传统模型相比，发电量增加0.552亿kW·h，弃水量减少1.694亿m3。

本文提出了应用Benders分解算法求解两阶段随机优化模型，但目前该方法只能处理线性问题。如何增强其求解非线性问题的能力，获得更有效、更可靠的调度方案，将是下一步研究的重点。

参考文献：

［1］ 王永真，康利改，张靖，等.综合能源系统的发展历程、典型形态及未来趋势［J］.太阳能学报，2021，42（8）：84-95.

［2］ 申建建，王月，程春田，等.水风光多能互补发电调度问题研究现状及展望［J］.中国电机工程学报，2022，42（11）：3871-3885.

［3］ 周建中，杨佩瑶，覃晖，等.水库（群）随机优化调度研究进展与展望［J］.华中科技大学学报（自然科学版），2022，50（8）：19-26.

［4］ 张俊涛，程春田，于申，等.水电支撑新型电力系统灵活性研究进展、挑战与展望［J/OL］.中国电机工程学报，1-22［2024-05-23］.

［5］ GONZALEZ-APARICIO I，ZUCKER A.Impact of wind power uncertainty forecasting on the market integration of wind energy in Spain［J］.Applied Energy，2015，159：334-349.

［6］ PURVINS A，ZUBARYEVA A，LLORENTE M，et al.Challenges and options for a large wind power uptake by the European electricity system［J］.Applied Energy，2011，88（5）：1461-1469.

［7］ NAZARI-HERIS M，MOHAMMADI-IVATLOO B B，GHAREHPETIAN G.Short-term scheduling of hydro-based powerplants considering application of heuristic algorithms：A comprehensive review［J］.Renewable and Sustainable Energy Reviews，2017，74：116-129.

［8］ 程春田，武新宇，申建建，等.亿千瓦级时代中国水电调度问题及其进展［J］.水利学报，2019，50（1）：112-123.

［9］ 谢俊，鲍正风，曹辉，等.金沙江下游水风光储联合调度技术研究与展望［J］.人民长江，2022，53（11）：193-202.

［10］明波，李研，刘攀，等.嵌套短期弃电风险的水光互补中长期优化调度研究［J］.水利学报，2021，52（6）：712-722.

［11］闻昕，秦济森，谭乔凤，等.基于余留期效益函数的水光互补随机优化调度方法［J］.水资源保护，2023，39（6）：23-31，62.

［12］CAO H，QIU J，ZHUO H M，et al.A long term operational scheme for hybrid hydro photovoltaic（PV） systems that considers the uncertainties in reservoir inflow and solar radiation based on scenario trees［J］.Water Resources Management，2023，37：5379-5398.

［13］ZHANG Y，CHENG C T，CAO R，et al.Multivariate probabilistic forecasting and its performance’s impacts on long-term dispatch of hydro-wind hybrid systems［J］.Applied Energy，2021，283：116243.

［14］HU W，ZHANG H X，DONG Y，et al.Short-term optimal operation of hydro-wind-solar hybrid system with improved generative adversarial networks［J］.Applied Energy，2019，250：389-403.

［15］赵志鹏，于志辉，程春田，等.水风光综合基地多风险量化及长期多目标协调优化调度方法［J/OL］.电力系统自动化，1-17［2024-05-23］.

［16］LI H，LIU P，GUO S L，et al.Long-term complementary operation of a large-scale hydro-photovoltaic hybrid power plant using explicit stochastic optimization［J］.Applied Energy，2019，238：863-875.

［17］YANG Z，LIU P，CHENG L，et al.Deriving operating rules for a large-scale hydro-photovoltaic power system using implicit stochastic optimization［J］.Journal of Cleaner Production，2018，195：562-572.

［18］吴洋，苏承国，孙映易，等.现货市场环境下水电富集电网日前优化调度研究［J］.人民长江，2023，54（7）：210-217，233.

［19］赵书强，金天然，李志伟，等.考虑时空相关性的多风电场出力场景生成方法［J］.电网技术，2019，43（11）：3997-4004.

［20］HEITSCH H，ROMISCH W.Scenario reduction algorithms in stochastic programming［J］.Computational Optimization and Applications，2003，24（2/3）：187-206.

（编辑：郑 毅）

Long-term optimization scheduling method for hydro-wind-PV multi energy complementary systems considering multi uncertainty

CAO Hui1，2，MU Changxing3，YANG Yuqi1，2，XU Yang1，2，ZHANG Zheng1，2，CHENG Chuntian3

（1.China Yangtze Power Co.，Ltd.，Yichang 443002，China； 2.Hubei Key Laboratory of Intelligent Yangtze and Hydroelectric Science，Yichang 443002，China； 3.Institute of Hydropower & Hydroinformatics，Dalian University of Technology，Dalian 116024，China）

Abstract：

Multi uncertainty of hydro-wind-PV systems and its optimal solution with high dimension is a key challenge in the lonOQ+rGi0w3WR/Y54sXoiJJ1/+kXawvbYgaNicVHrQ3eE=g-term scheduling of hydro-wind-PV multi energy complementary systems.By employing a hydro-wind-PV scene generation method based on Markov chain and Copula function，and utilizing a reduction technique to reduce the number of scenes，the uncertainties of the hydro-wind-PV system can be quantified.Taking the reduced scenes as input，we developed a long-term two-stage stochastic optimal scheduling model that incorporates Benders decomposition algorithm and convex linearization to realize high efficient solution for high dimension problems.The model was used to simulate the scheduling process of a clean energy base in downstream of Jinsha River，which demonstrated the method's effectiveness in enhancing adaptability to the uncertain hydro-wind-PV systems and in improving overall benefits.In out-of-sample testing，the proposed method increased 55.2 million kWh power generation and decreased 169.4 million m3 abandoned water compared to traditional methods，demonstrating a greater performance.

Key words：

hydro-wind-PV complementary systems； long-term scheduling； two-stage stochastic optimization； Benders′ decomposition