二分图中高效计算top-n maximal α-biclique的方法研究

关键词：（1，α）-core;maximal α-biclique;共同邻居;节点顺序

中图分类号：TP391 文献标志码：A

0 引言（Introduction）

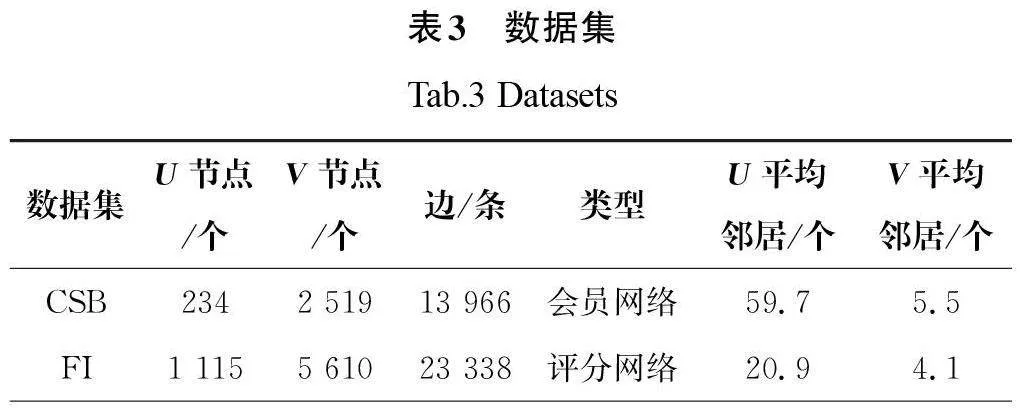
二分图是社交网络中一个备受关注的研究领域[1]，通常被用于两种不同类型的实体及两类实体之间的联系建模。当前的研究主要聚焦于根据给定查询用户及查询参数，输出符合查询条件的稠密子图[2-3]，或者通过直接遍历子图获得整个二分图上所有的稠密子图[4]。但是，当用户只给定某一类节点的组合数量，希望输出另一类节点数量排序为前n 的子图时，现有的研究不能很好地解决这个问题。针对上述问题，本文提出了两种不同的搜索算法：基础搜索算法和基于共同邻居搜索算法。基础搜索算法使用（1，α）-core剪枝方法简化初始图，该算法必须遍历简化图中全部节点，才能获得所有的maximal α-biclique。基于共同邻居搜索算法，每次选择顺序最大的节点进行遍历，并且只枚举该节点的二跳邻居，当已经获得n 个maximal α-biclique时，根据当前最小阈值判断是否提前结束算法。实验结果表明，两种算法都可以有效地解决上述问题，与基础搜索算法相比，基于共同邻居搜索算法的搜索效率提升了80%。

1 相关研究（Related work）

1.1 二分图中的常用模型

LYU等[5]研究了大规模二分图中进行最大biclique搜索的问题。他们设计了一种渐进式边界框架，该框架通过将问题映射到二维空间进行分析，利用节点性质缩小子图从而提高搜索效率，并通过阿里巴巴集团控股有限公司的真实数据集验证了算法的有效性。LIU等[6]提出了一种基于索引的（α，β）-core分解算法，并介绍了实用的索引维护方法。该分解算法的运行时间复杂度为O（n），其中n 为节点数量，索引仅需要O（m）大小的空间存储，其中m 为边的数量。杨珍等[7]提出了基于加权二分图的推荐方案，采用基于用户和方案特征的评分方式组成用户方案规则库，使用协同过滤算法比较新用户特征和规则库中用户特征的相似度，并选择相似度高的进行推荐。

1.2 二分图中的biclique计数问题研究

蝴蝶计数作为biclique计数问题的一个特例，近年来引起了许多研究者的关注。WANG等[8]首次提出了二分图中蝴蝶计数的精确算法，该算法避免了枚举所有的蝴蝶。首先，算法随机选择一层节点;其次，对于所选层中的每个节点u，计算它的二跳邻居。对于u 的每个二跳邻居w，计算出u 和w 之间的共同邻居数量，就可以得到包含u 的蝴蝶数量。将所有节点的蝴蝶数量相加再除以2，就是蝴蝶的总数。ZHOU等[9]定义了不确定二分图上的蝴蝶结构，提出了蝴蝶结构的计数问题，在基础搜索算法的基础上提出了改进算法。该改进算法在不增加内存成本的情况下，进一步使用启发式策略减少程序的运行时间。在不需要获得精确结果的情况下，可以通过抽样方法获得近似结果。YANG等[10]研究了二分图中的bi-triangle计数问题，其中bi-triangle被定义为6-cycle。

1.3 二分图中的biclique枚举问题研究

一个与本文的研究密切相关的问题是二分图中的maximal biclique枚举。只有当一个biclique不被其他任何biclique包含，才被称为maximal biclique。ABIDI等[11]发现基于枢轴的搜索空间修剪在集团枚举中有效，于是他们提出了一种实现枢轴修剪的算法，并通过对节点进行离线排序，达到加快修剪的目的。SHAHAM 等[12]提出了一种使用蒙特卡洛子空间聚类方法寻找最大边团的概率算法，并证明了该算法的有效性。CHEN等[13]证明了在实际应用的二分图中可以快速地发现最大平衡二分团，并且针对小型稠密图和大型稀疏图分别提出不同的精确算法;针对典型的大型稀疏图，他们还提出了一种将大型稀疏图转换为有限数量的稠密子图的算法。

2 常用符号和基础定义（Frequently used notationsand basic definition）

在二分图中有许多常用的符号，这些符号会在本文中重复出现，为了不重复描述同一个符号，也便于查找符号对应的解释，本文将常用符号和对应的解释全部列于表1中。

本文中经常使用的定义如下。

3 基础搜索算法（Basic search algorithm）

针对当二分图中一类节点的数量固定时，如何搜索另一类型节点数量排序为前n 的maximal α-biclique的问题，最简单的解决方法就是直接枚举二分图中所有的maximal α-biclique，最后从结果集中找到V 节点数量最多的排序为前n 个的maximal α-biclique。但是，这种方法是极其耗费时间的，尤其是在二分图非常大的情况下。因此，本文首先根据maximal α-biclique的性质进行剪枝，其次在经过剪枝之后的简化图中进行maximal α-biclique枚举。剪枝条件和枚举算法如下。

引理1：在二分图G 中被包含在maximal α-biclique的节点一定被包含在（1，α）-core中。

证明：可以使用反证法证明。如果一个U 类型节点出现在maximal α-biclique中，那么该节点的邻居数量一定大于1，如果这样的节点不被包含在（1，α）-core中，那么与定义1相违背。同理，如果一个V 类型节点出现在maximal α-biclique中，那么该节点的邻居数量一定大于α，如果这样的节点不被包含在（1，α）-core中，那么也与定义1相违背。

基础搜索算法首先从原始二分图中获得经过（1，α）-core剪枝的简化图（第1行）;其次将优先级队列C 和已遍历节点队列Q 进行初始化（第2行）;再次对简化图中的U 类型中的每一个节点进行递归，找到符合要求的maximal α-biclique，同时将已经遍历过的节点添加到队列Q 中（第3～5行）;最后从优先级队列C 中将前n 个结果返回（第6行）。

Enumeration子过程是用来枚举maximal α-biclique的具体算法。调用Enumeration子过程时需要传入4个参数。双向队列L 中存放已经选中的节点，数组C中存放可以添加到双向队列L 中的节点，集合R 中存放双向队列L 中所有节点的共同邻居，整数index 则表示C 中下一个要被遍历的节点下标。Enumeration算法首先会判定双向队列L 中节点的数量和C 中还未遍历节点的数量之和是否小于α，如果判定成立，就直接返回，不再向下递归（第8～9行）。当判定成立时，当前选择的节点集合不可能成为一个maximal α-biclique，当前枚举过程可以提前结束。当判定不成立时，会继续判断当前双向队列L 中节点的数量是否等于α，如果成立，那么就把当前双向队列L 和集合R 中的节点添加到优先级队列C 中，并且返回（第10～12行）。当双向队列L 中的节点数量小于α 时，从数组C中选出下标为index 的节点u'添加到双向队列L中，集合R中的节点更新为集合R中节点和u'邻居节点的交集，并进行下一层的递归，当递归完成后，将双向队列L 和集合R中的节点恢复为此次遍历之前的节点集合（第13～16行）;具体的算法过程如下。

引理2：基础搜索算法可以正确地输出top-n maximal α-biclique。

证明：为了证明算法返回的是正确的结果，需要证明在删除不满足要求的节点时，G总是包含最大（1，α）-core。显然在第一行初始化G 时，它包含了最大（1，α）-core，而且在对U 中的节点进行遍历时，也没有删除节点，所以可以确保所有的节点都被遍历，不会遗漏任何一个maximal α-biclique。同时，队列Q 会记录遍历过的节点，并在数组C中已将遍历过的节点全部排除，不会出现同一个maximal α-biclique重复出现的情况。因此，引理2正确。

复杂度分析：给定一个二分图G=（U，V，E），基础搜索算法的时间复杂度是O（|U|α），其中Uc 为简化后子图包含的U类型节点。

4 基于共同邻居的搜索算法（Search algorithmbased on common neighbors）

虽然基础搜索算法可以成功计算出top-n maximal α-biclique，但是它仍有优化的空间。比如基础搜索算法在数组CL 中存放的是Uc 中除了已经遍历过的节点外的所有节点，但实际上对于Uc 中的一个节点u'，如果u'不是节点u 的二跳邻居，那么u 和u'之间的共同邻居数量一定为0，u 和u'一定无法满足maximal α-biclique，因此会导致一些无效搜索过程。基于此观察，本节介绍基于共同邻居的搜索算法。

4.1 基于共同邻居的搜索策略

二跳邻居的定义如下。

定义4：二跳邻居。在一个二分图G=（U，V，E）中，如果节点u 和节点v 之间存在一条边（u，v），同时节点v 和节点u'之间也存在一条边（u'，v），那么称u'是u 的二跳邻居。

同时发现，本文的求解目标是top-n maximal α-biclique，因此只需要求解出排序为前n 个的maximal α-biclique即可，不需要枚举出所有的maximal α-biclique，因此本文使用了节点顺序的概念，如定义5。节点顺序排名高的节点，优先进行遍历。一个节点的节点顺序越大，那么在该节点组成的maximal α-biclique中，V 中元素数量越多的可能性越高。

定义5：节点顺序。给定一个二分图G=（U，V，E），对于两个节点u，u'∈U，如果节点u 的邻居数量d（u，G）>d（u'，G）或者d（u，G）=d（u'，G）并且u.id<u'.id，那么u的节点顺序高于u'的节点顺序。

如果当前结果集中maximal α-biclique的数量已经到达n个，同时一个节点的共同邻居数量小于或等于当前结果集中最小maximal α-biclique中V 的节点数量，那么要遍历的U类型节点形成的maximal α-biclique就不会出现在结果集中。这个现象可以被用来搜索空间剪枝。

4.2 算法设计

根据以上观察结果，本文设计了基于共同邻居搜索算法，算法流程具体如下。

基于共同邻居搜索算法的第一步和基础搜索算法相同，都是先对原始图进行（1，α）-core剪枝得到简化图（第1行），然后将优先级队列C 初始化为空，同时将阈值min设置为0。min用来记录当优先级队列C 的大小为n 时，优先级队列C 包含的各个maximal α-biclique中V 类型节点数量的最小值（第2行）。算法将所有节点的二跳邻居存放到集合NN 中，并根据每个节点的度计算出节点的排序（第3～4行）。根据此节点的排序按逐渐降序的方式进行遍历（第5～11行），如果当前节点的邻居数量小于或等于阈值min，那么表示此节点包含的maximal α-biclique不可能优于当前已知结果，因此直接结束此次循环（第6～7行）。如果当前节点的二跳邻居数量大于或等于α-1，那么对该节点可能形成的maximal α-biclique进行枚举。当前节点遍历完成后，需要更新集合NN ，防止枚举相同的maximal α-biclique。

PBlisting子程序是实现枚举过程的具体算法，需要传入3个参数：集合W 用来存放u 的二跳邻居，集合CommonN 存放L 中所有节点的共同邻居，双向队列L 存放当前候选的所有节点。当双向队列L 中的节点数量为α 时，判断当前集合CommonN 中的节点数量以及优先级队列C 的大小，如果集合CommonN 中的节点数量大于min，同时优先级队列C 中maximal α-biclique数量等于n，那么将优先级队列C 中V 节点数量最少的maximal α-biclique 弹出，将新的maximalα-biclique加入优先级队列C 中，并且更新参数阈值min。如果优先级队列C 中maximal α-biclique数量小于n，那么同样将新的maximal α-biclique插入优先级队列C，并且若插入后优先级队列C 中maximal α-biclique的数量等于n，则更新阈值min，最后返回（第14～21行）。如果L 中节点的数量小于α，同样根据节点的顺序，每次选择集合W 中顺序最高的节点添加到双向队列L 中，直到程序结束。基于共同邻居搜索的算法伪代码如算法2所示。

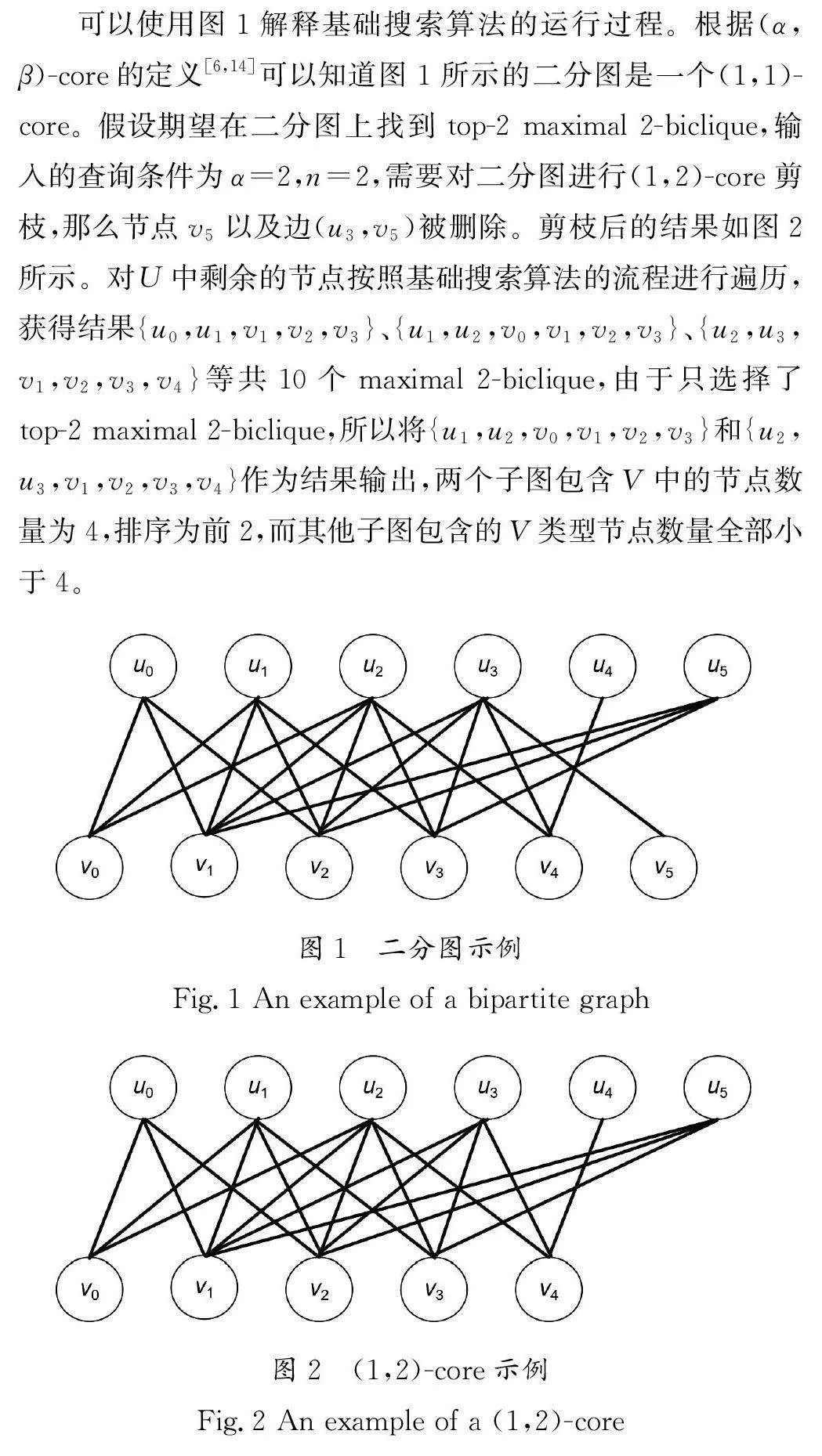
4.3 算法运行实例

使用图2模拟基于共同邻居搜索算法遍历节点的过程。节点的遍历顺序和结果集的变化过程如表2所示，查询参数同样为α=2，n=2。

5 实验（Experiments）

5.1 实验环境和数据集

实验环境：本研究在CSB、FI、MI和LA真实数据集上对本文提出的算法进行实验评估，以验证算法在不同数据集上的有效性。所有实验都是在一台配置为Intel i5 3.1 GHz CPU和16 GB内存的Windows机器上运行的。算法全部由Java语言编写。

算法：使用基础搜索算法和基于共同邻居算法验证top-nmaximal α-biclique。为了方便表述，以下使用BL和CN分别表示基础搜索算法和基于共同邻居搜索算法。

数据集：从不同领域选择了4个真实数据集，这些数据集具有不同的数据属性。所有的数据集都可以在Konect（www.konect.cc）上获得，数据集的详细信息如表3所示。

参数设置：为了更好地评估本文提出的算法，本文将n 的参数范围设置为10～100，每次增加30，同时α 的范围设置为3～11，每次增加2。同时，如果没有特殊说明，那么实验中默认使用n=10，α=3作为参数。

5.2 算法运行时间分析

不同数据集上的实验结果：BL和CN在不同数据集上的运行时间如图3所示。从图3中可以观察到，在所有数据集上，CN的运行时间比BL的运行时间增加了接近一个数量级。这是因为CN剪去大量的无效分支，并能够在已确信获得所需结果的前提下提前终止算法的运行，从而节约了计算时间。当U 类型的节点增加时，BL的运行时间快速增加，但是CN运行时间增加缓慢，说明CN具有良好的剪枝效果。

参数n 变化的效果：表4展示了当查询参数α=3时，BL和CN在4个数据集上随着n 从10变化到100时的运行时间变化情况。从表4中可以观察到，BL的运行时间没有发生变化，这是因为BL每次都要获取所有的3-biclique。CN的运行时间随着n 的变大而增加，但是增加的幅度十分缓慢，这是因为当n 的值变大时，要返回的maximal 3-biclique数量更多，此时阈值可能变小，必须遍历更多的节点，才可以获得结果。

参数α 变化的效果：图4展示了当n=10时，BL和CN在4个数据集上随着α 从3变化到11的运行时间。从图4中可以观察到，CN在4个数据集中的运行时间没有剧烈的变化且远远小于BL的运行时间。在CSB和FI中，BL的运行时间随着α的增加呈现先增加后减小的变化趋势。这是因为当α很大时，简化图就会变得比较小或者比较稀疏，此时BL可以很快地枚举整个子图。在MI和LA中，简化图虽然变小，但是仍有大量的节点需要遍历，因此BL的运行时间随着α的增加而增加。

5.3 算法剪枝效果分析

α变化的剪枝效果：表5展示了随着α 的变化，BL和CN需要遍历的节点数量。从第二列到第五列，每一列左边和右边的数字分别表示BL与CN需要遍历的节点数量。从表5中可以观察到，随着α 变大，BL遍历的节点数量逐渐减少。这是因为当α 变大时，使用（1，α）-core剪去U 类型节点的数量增加，U中剩余的节点数量变少，需要遍历的节点也变少。然而在CN中，每次都选择排序最大的节点枚举，则越有可能成为结果的节点就会越早被遍历到，当已经获得数量为n 的maximal α-biclique后，就可以通过阈值判断是否结束算法。

n 变化的剪枝效果：表6展示了当n 变化时，BL和CN需要遍历的节点数量。从第二列到第四列，每一列左边和右边的数字分别表示BL和CN需要遍历的节点数量。从表6中可以观察到，当n 变大时，BL需要遍历的节点数量是一样的，n 变大时，经过（1，3）-core剪枝的简化图的大小没有变化，BL每次都要遍历所有的U 类型节点。CN需要遍历的节点数量随着n的变大而不变或增加，这是因为当n 变大时，阈值可能会变小，只有遍历更多的节点，才能确定最终结果。

6 结论（Conclusion）

本文研究当二分图中某一类节点的数量固定时，如何搜索包含另一类型节点数量排序为前n 的maximal α-biclique问题。首先，本文介绍了maximal α-biclique的定义。其次，提出了一种使用（1，α）-core剪枝的基础搜索算法，并在该算法的基础上利用共同邻居概念提出了基于共同邻居搜索算法。基于共同邻居搜索算法每次选择排序最大的节点遍历，通过枚举该节点的二跳邻居减少搜索分支，并且根据已知结果的最小阈值，判断是否能提前结束搜索过程，从而提高搜索效率。最后，本文通过理论分析和广泛的实验验证了两种算法的有效性，同时实验结果表明，相比于基础搜索算法，基于共同邻居搜索算法的搜索效率提升了80%。

作者简介：

唐东杭（1997-），男，硕士生。研究领域：数据挖掘，社交分析。

吴进高（1977-），男，本科，工程师。研究领域：数据挖掘，社交分析。本文通信作者。

徐建（1975-），男，博士，教授。研究领域：数据挖掘，社交分析。