指向学生思维发展的小学数学“1与多”辩证认知策略

摘要：学生对数的认识经历了基于具体物体的单个量的认知到借助计数单位和理解数量关系的抽象认知阶段，实现了对从“1”到“多”的辩证理解。教师应提炼基于量化表述、定性描述和模型刻画的认知策略，以促进学生的认知从“1”走向“多”、从“量”走向“计数单位”，最终达成从“量”到“率”的转变，进而发展数学思维。

关键词：1与多；辩证；认知策略；思维发展

小学阶段“数的认识”领域是在不断经历“1与多”的辩证认知过程中行进的，可分为“数量的累加”“位值的拓展”“关系的增减”三个阶段，本文将结合具体案例阐述这三个阶段的认知策略。

一、量化表述：实现“单个量”到“多个量”的叠加

建立正确的数概念是认数教学的任务，也是学生数学学习的起点。理解数的意义一般有两个角度：一是立足数的组成，指基于元素和集合的角度，运用组成理解数的大小和多少，加强对数的感知；二是联系生活实际，指出通过具体的现实情境理解数在生活中的意义，使抽象的数和具体的量有机结合，从而进一步理解数的意义。实际教学中，教师应将这两种方式有机融合。一年级是学生系统认数的开始，学生眼中所见的每一个物体都可“数”，根据这一年龄段学生的认知特点，对于数概念的建构应以具体直观为主，引导学生在操作中推动思考，在思考中感悟数的叠加性。

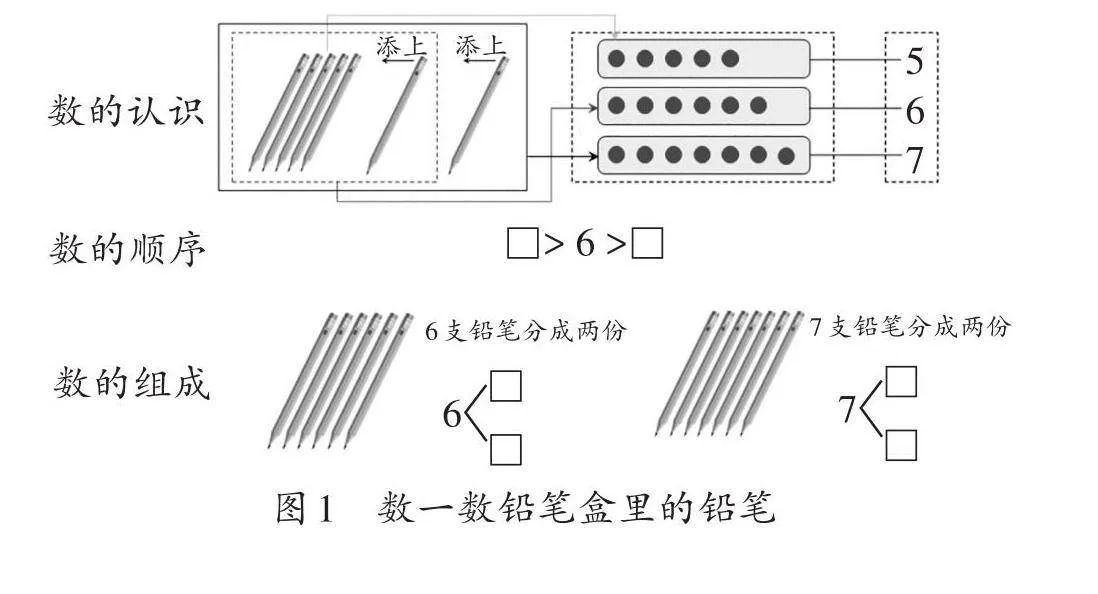
例如，在教学“6，7的认识”时，教师可创设“数一数铅笔盒里的铅笔”的真实情境（如图1），让学生经历从具体实物到半抽象的点子图，再到抽象的数。

学生经历以下思考：一是5支铅笔添上1支是几支铅笔？继续添，有什么发现？二是□ > 6 > □，□里可以填几？三是如果把6支铅笔分成两份，可以怎样分？其中的一份有可能是7支吗？

学生对数的认识从具体走向抽象，体会量一个一个的叠加，理解数的意义，初步感知每一个数即为1个元素；掌握数的大小和顺序，体会每一个元素都能找到一个后继的元素，由此可得：一个又一个元素可以组成一个无穷的集合。

二、定性描述：实现“1个数”到“1个计数单位”的递进

（一）感官体验，借实物感知“1到多”的辩证关系

在“1到多”的累加过程中，当数量达到10时，实现了数到计数单位的飞跃。教师要把握“10的认识”教学关键点，提供丰富的素材，如散放的10颗糖、一盒鸡蛋（10个）、一包口罩（10只）、一对娃娃、8个苹果，引导学生寻找能用10表示的物品。学生通过数一数确定“10”；运用数的组成确定一盒鸡蛋里有两个5正好是10个；借助文字信息确定一包口罩的数量是10只。

fcIP7JjL8s51tsgLvtEisw==一方面，学生通过观察，将颜色、形状、大小等非本质元素剥离，经历了从物抽象到数的过程：10颗糖一颗颗地数，一盒鸡蛋5个5个地数，体验加“1”组成“多”的累加过程。另一方面，学生理解10个物体可以分为多个个体，感悟“多”可以分解为若干个“1”，明确“多”包含“1”。感悟“1到多”的辩证关系，能帮助学生全面、正确地理解相对抽象的数字“10”，并再次强化“1到多”的数学概念。

（二）具身操作，借学具感悟“1与多”的辩证关系

在数的认识过程中，教师要运用多种模型帮助学生理解数的意义，如计数器、方格图、数位顺序表等；要借助直观素材进行具象化的表示，提供多元化的学习材料作为学习支架，促进学生多感官协同参与，从而逐渐建立起抽象的数和现实中的数量之间的关系，促进辩证关系的渗透。

在“创造10”的环节中，教师可引导学生借助学具表示10，并根据学生呈现的不同表征方式，了解学生的思维水平。教师可让学生对四种不同的表示方法（10根小棒摆一行，表示10个一；10根小棒扎成一捆，表示1个十；计数器个位摆10颗珠子，表示10个一；计数器十位摆1颗珠子，表示1个十）进行深入辨析，探寻异同点，感受“1”包含于“多”、聚“1”为“多”的辩证关系，对后续数的认识起到正向迁移作用。

一是辨析1根与1捆。学生经历1根小棒记作1个一，一捆小棒记作1个十，辨析“1个一”与“1个十”中的“1”，第一次感受对立统一现象（即同一个数字“1”表示的具体意义不同）：第一个“1”表示1根，第二个“1”表示1捆（10根）。在相同数字“1”中，学生能感受到计数单位的必要性。

二是辨析10根与1捆。学生经历10根小棒扎成1捆，从10个一到1个十的转变，体会虽然表示的具体数量相同，但是从形态上看，10个一根是分散的，而1个十是捆在一起看作一个整体的，区分多个“个体”和1个“整体”，初步感知计数单位的重要性。学生借助“捆一捆”的操作体会1个十中包含着10个一，感受“多”包含于“1”的辩证关系。

三是辨析计数器上的1颗与10颗。同样是用小棒表示10，不管是10根还是1捆，都包含了10根，都可以用计数器表示。教师引导学生思辨：计数器个位上摆10颗珠子勾联10根小棒的表示方法，一颗珠子和一根小棒对应，理解计数器个位上10颗珠子表示10个一；而计数器十位上摆1颗珠子则对应1捆小棒表示1个十。学生感受1颗珠子在不同数位上的意义，加深对10个一是1个十的理解，为后续学习计数单位及数的组成作铺垫。

（三）辨析对比，借计数器明晰“1与多”的辩证关系

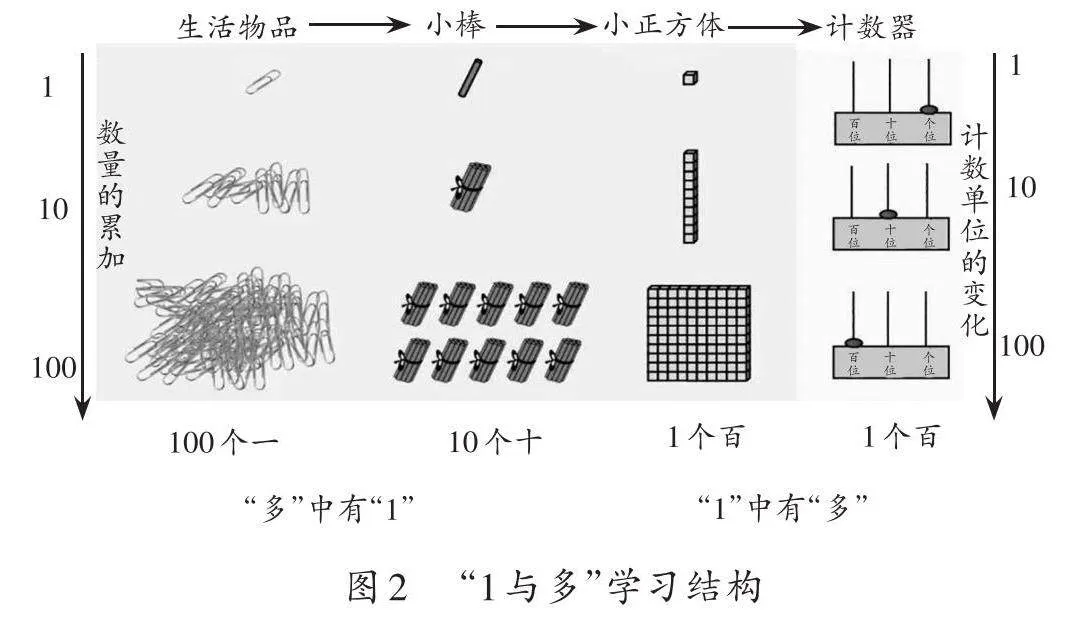
教师引导学生借助小棒、小正方体、点子图、计数器等表示100，辨析100个一、10个十、1个百，感悟多元表征下的相同本质。学生再次感悟“1与多”的辩证关系，为学习更大的数做好辩证方法的储备（如下页图2）。

一是体验表征方式，剖析形态下的本质。教师引导学生借助小方块、小棒、计数器等学具表示100，通过对比揭示“1与多”辩证关系的三个层次。层次一，相同学具、数量，不同形态表征100，体会形态不同而数量相同。层次二，不同学具、相同数量表征100，感知表征方法不同而数量相同。层次三，不同学具、不同数量表征100，再次感悟表征方法不同而数量相同。学生深入理解“1”大捆与计数器上百位的“1”颗珠子都能表征100，进一步发展“1与多”的辩证思维。

二是聚焦计数单位，感悟位置制的价值。教师引导学生连接旧知，回忆1个一的含义及10个一就是1个十，并在100的认识过程中经历1个十到10个十的累加，理解10个十就是1个百。学生聚焦计数单位，辨析1个一、1个十和1个百中的“1”，发现同样都是数字“1”，所在的数位不同，所表示意义不同，数量也就不同，感悟“1”既可以表示“单”个数量，也可以表示“多”个数量，体会位置制的应用价值。

三是丰富表象特征，探寻相同数的意义。学生借助学具表征并经历从直观到抽象的过程，提炼100个一、10个十和1个百，感受同样都表示100但表示的意义不同。教师引导学生想象：在计数器上，100个一就要在个位拨100颗珠子，10个十就要在十位拨10颗珠子，而1个百则只要在百位拨1颗珠子，学生在进一步辨析中体会计数器表示数的简明性，感悟计数单位的重要性，体会“1”能表示10还能表示100甚至更多，进而理解“1”中蕴含着“多”，强化“1与多”的辩证关系。

（四）迁移统整，借数位顺序表明晰“1与多”的辩证关系

学习“小数的意义”之前，学生对于数位顺序表的认知主要停留在从右往左的顺序中，即计数单位间基于“10”的不断递进，而小数实际上是十进制计数法向反方向延伸的结果，即基于“1”的不断细分。在学生的经验处逆向发问，能够帮助学生跳出常规思维，走向知识的迁移与重整。

一是计数体系的迁移。第一次迁移是从整数到小数的迁移。教师通过提出“如果从数位顺序表的左方往右看，还能继续分吗？怎么分？”的大问题来驱动学生思考，使学生明确1与[ 110 ]的关系，进而将十进制计数法从整数推到小数。第二次迁移，是从[ 110 ]类推迁移。教师赋予学生[ 110 ]计数单位的概念，要求明确[ 110 ]在数位数值表中的位置以及相应的数位，学生根据已有的细分经验以及数位顺序表的规律，依次往后推出计数单位以及相应的数位。

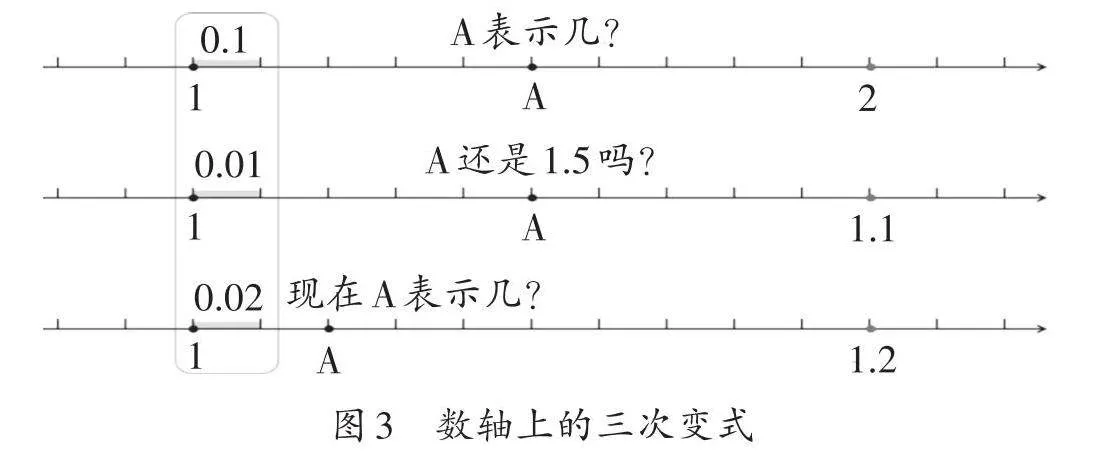
二是计数单位的统整。教师以半抽象化的数轴为学习素材，通过三次变式，让学生在不断重组、打破、调整和应用的过程中，明确一格表示几是推理A的关键（如图3）。同时，通过一格表示0.02的呈现，教师能够帮助学生打破思维定势，统整“单位”的概念：这里的一份实际上是基于数学学习的需求和交流的需要而规定的“单位”，但不论怎么变，单位的连加与细分其实都是一致的。

三、模型刻画：实现“数量”到“关系”的飞跃

【第一次飞跃】“倍的认识”帮助学生实现了对于数的认知从关注“具体的量”走向关注“抽象的关系”，勾联了量的认识和率的感知，为后续学习分数做好了认知铺垫，是一次质的飞跃。

教学不能仅仅停留于通过具体实物的对比来感知两个量之间的具体倍数关系，教师还要力图打破实物图所带来的固化模式。例如，教师可引导学生借助几何直观的方法，将3个篮球抽象为一条线段，引导学生大胆思考：“是否可以将篮球的数量表示为任何数？”学生体会到足球的数量会随着篮球数量的变化而变化，但这两种球之间的关系却是不变的，以此来把握倍的基本概念。同时，教师可引导学生在思考与辨析中初步感悟：无论篮球的数量是多少，都可以用一条线段来表示。这就打破了“数的认识”中十进制计数法只能将“10个”看作一个整体的思维局限，使学生辨析一条线段或者一份中可以是单个量，也可以有多个量，凸显理解标准量的重要性及“1与多”的相对性（如图4）。

【第二次飞跃】“分数的意义”一课是在学生直观认识分数基础上对概念进行二次学习，侧重对分数“比率”维度的意义理解与深化：分数既是对部分与整体的关系表达，又是对两个独立量比较关系的呈现。基于前序经验，学生能够利用手中的素材表征 [13] ，但对于同一分数不同表示形式下的异同没有很深的感悟。学生通过聚焦、对比与发散，提炼分数的本质，进入意义理解的另一水平（如图5）。

一是在不变中提炼部分与整体的关系。学生聚焦作品1和作品2，这是他们最为熟悉的分数表征方式之一。通过“还可以用几个圆表示出 [ 1 3] ”“为何都能表示[ 1 3] ”的问题引领，学生在变化的部分量和整体量中发现不变的关系，从而实现分数模型的建立。学生再由“这个整体还可以是什么？”发散思维，在不断体验聚多个物体为一个整体的过程中强化“多”包含于“1”的辩证关系，丰富单位“1”的内涵。

二是在经验处勾勒两个独立量的关系。聚焦作品3，学生在“为何两行圆也能表示 [ 1 3] ”的思维冲击下，将“分数”与“倍”进行关联，感知两者都是基于“1与多”的比较得到的，不同之处在于标准量的选择。将阴影圆看作一份，并作为标准时，两者的关系可以用倍数呈现；而将空白圆看作单位“1”时，两者的关系则是用分数表示的。学生由此体会“一倍数”与单位“1”的一致性，实现对分数意义的进一步理解，即向表示两个量之间的关系递进。

三是在发散中展露分数率视角的全貌。学生再次聚焦作品2，借同一素材的多角度思考，跳出单一思维，强化对分数能够表示两种关系的理解。从“同样这6个圆还能一眼看出什么分数”到“为什么想到了不同的分数”，学生在逐步深入中明确单位“1”与分数单位的重要性，同时在体验细分单位“1”与累加计数单位的过程中，深化“1与多”的辩证关系。

在教学中，教师要基于辩证的视角聚焦“1与多”关系的内容，引导学生在感性探究中开展理性思辨，揭示“1与多”的相对性、绝对性和包含性，以此增进对数学知识的理解，从中积累数学经验，建立数学认知，促进高阶思维的发展。

参考文献：

［1］寇敏娟. 论教学中的“一”与“多”［J］. 太原师范学院学报（社会科学版），2009（3）.

［2］郑和钧. 渗透“1”与“多”辩证关系的方法［J］. 湖南教育，1987（5）.

（责任编辑：杨强）