数学实验在小学数学概念教学中的应用探究

摘要：数学实验指的是运用“做数学”理论，借助物化的工具，让学生基于实验目标，进行规范的实验操作和相应的数学化分析，个性化地建构数学的意义，发展数学思维和创新意识。在小学数学概念教学中应用数学实验，学生不仅能掌握数学的基本知识和基本技能，还能获得数学的基本活动体验，培养数学核心素养。

关键词：小学数学概念教学；数学实验；数学核心素养

概念教学是小学数学教学的难点之一，有些概念并非直接来源于实际问题，距离学生的生活实际较远。小学生由于自身的理论知识储备不足，抽象能力较弱，导致较难深刻理解数学概念，也难以有效地应用数学概念来解决生活中的实际问题。数学实验是学生学习数学的有效方法之一，通过数学实验，学生不仅能掌握数学的基本知识和基本技能，还能获得数学的基本活动体验，从而发展思维，提升数学核心素养。下面，笔者以人教版小学数学教材五年级下册“公倍数和最小公倍数”一课为例，探索数学实验在数学概念性知识教学中的应用实践。

一、让学生参与设计实验，初步理解数学概念

数学概念本身的抽象性，导致学生存在理解的困难。在进行数学概念教学时，教师可让学生参与设计数学实验，确立实验目标和实验步骤，并在“做”中学、在“做”中体验。这样，就可以让学生在操作、讨论中初步理解数学概念的本质。

（一）玩一玩、说一说，在单人走格子实验中理解“倍数”的含义

【教学片段1】

师：我们来做一个简单的单人走格子实验，下面请先看视频里的姐姐是如何进行实验的。姐姐接到的指令是“每次走2格”，我们先来猜一猜，姐姐会走进哪些格子？为什么？

生：2，4，6，8……走进的格数都是2的倍数。

师：事实真如你们猜想的那样吗？我们一起来看。如果继续走下去，还会走进哪些格数呢？请拿出你信封里的指令，先来猜一猜，你走的格子数会有什么样的特点？

生：我走的格数可能是2的倍数，可能是5的倍数。

师：你们想到的格数和接下来走到的格数会是一样的吗？我们亲自来做一做实验。请你按照实验报告单（1）的步骤，开始你们的单人走格子实验吧。

实验报告单（1）

实验内容：单人走格子实验

实验目的：复习倍数

实验步骤：

1.走一走：每人按指令走格数。

2.想一想：圈出的数和拿到的指令有什么关系？

实验结论：我们发现，圈出的数和拿到的指令有（ ）。

师：由此，你们得到的结论是（ ），每次圈出的数都是拿到指令的（ ）。

（二）走一走、圈一圈，在双人走格子实验中理解“公倍数和最小公倍数”的含义

【教学片段2】

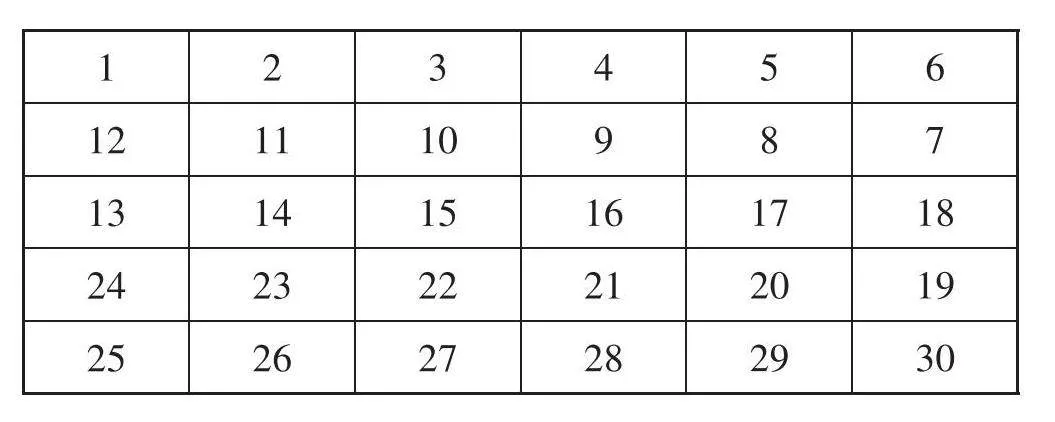
师：经过单人走格子实验，我们的猜想得到了验证。如果2个小朋友一起走格子，又会得到怎样的实验结论呢？我们一起来看双人走格子实验——小明打算每次走（ ）格，小红打算每次走（ ）格，我们猜棋子都会经过格数（ ）（ ）（ ）。游戏后，我们发现（ ）。谁看明白了实验的过程？请你来说一说。

师：现在请同学们拿出刚才的棋盘纸，同桌2人共用一张棋盘纸进行我们的双人走格子实验。实验前，我们先来看一下实验步骤——第一步是想一想，同桌两人各出一个数；第二步是猜一猜，你们可能会共同走进哪个格数；第三步是走一走、圈一圈，男生先根据自己出的数执子走数，圈出自己走进的格数；男生走完后，女生再根据自己出的数执子走数，用不同颜色的笔圈出自己走进的格数。

师：看明白实验步骤了吗？下面请你们翻开实验报告单（2），同桌2人按照要求进行实验，并填写实验报告单上面的内容。

实验报告单（2）

实验内容：双人走格子实验

实验目的：认识公倍数

实验步骤：

1.想一想：同桌两人约定，每人出一个格数。小明打算每次走（ ）格，小红打算每次走（ ）格。

2.猜一猜： 你们俩有可能会都跳进几号格？

我们猜想棋子都会经过格数（ ）（ ）（ ）。

3.做一做：借助棋盘走一走、圈一圈。

实验结论：我们发现，棋子都会经过的格数是（ ）（ ）（ ）。

教师分两个层次展示学生作业，层次一：看学生出的2个数，其他学生猜可能都走进了哪些格子，再揭示答案。层次二：先看共同走进的格子数，让学生猜是哪两个数。学生的作业纸板书有12，24，36，48，（4和6）或18，36，54（6和9）等。

师：为什么各组上报的相同数有差异呢？请同学们一起来找找原因。

生：我们接到的指令是4和6，所以我们共同走进的格子数是12，24，36，48。

生：我们接到的指令是6和9，所以我们共同走进的格子数是18，36，54。

师：看来这些数的出现（手指公倍数）都和接到的指令有关系，你能结合第一组数具体地说一说吗？

生：12既是4的倍数，也是6的倍数；24既是4的倍数，也是6的倍数。

师：你能给12，24起个新名字吗？（板书课题——公倍数）

师：36也能叫这个名字吗？（引导学生说36是4和6的公倍数）

师：公倍数一般写3个或3个以上，再写上省略号。4和6的公倍数有12，24，36……我们一起来看，这一列数有什么特点？

生：后面一个数都比前面一个数多12，后面的公倍数都是最前面12的倍数，12是4和6的公倍数中最小的一个公倍数。

（三）公倍数在实际生活中的应用

师：我们学习公倍数在生活有什么用呢？请看双人走格子实验——小虎和王军定期到敬老院帮助打扫卫生。小虎每4天去一次，王军每5天去一次。这个月的2日他们刚好同时去打扫卫生，那么这个月还有哪一天他们也同时去打扫卫生？

师：请同学们根据2023年5月份的日历先来想一想，经过多少天他们又同时去打扫卫生了呢？

生：20天，必须是4和5的公倍数。

师：那本月的几号他们俩又一起去敬老院打扫卫生了呢？

生：22号。

师：真的是这样吗？我们在日历上一起来走一走，圈一圈。请打开手里的日历，同桌两人一起来走一走吧。

师：通过双人走格子实验，我们认识了公倍数和最小公倍数，知道了两个数公倍数的个数是无限的。

抽象性的数学概念学生难以理解、消化，因此教师可以从学生生活中遇到的实际问题出发创设情境，设计数学实验，让学生在一定数学知识的基础上，在规范的流程操作下进行实验，通过数学化的分析，对数学概念性知识进行深刻理解和把握，并逐步形成具体的概念，使抽象的数学知识变得生动、有趣、易于理解。通过生活来创设情境，设计数学实验，学习数学概念，再以此解决实际问题，展示了数学概念的实际应用价值。

二、让学生数形结合，进一步理解数学概念

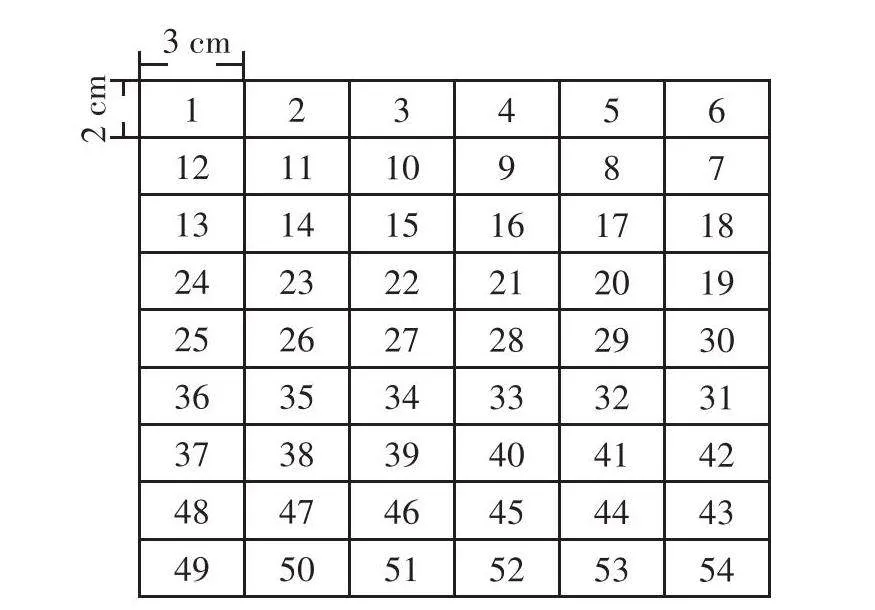
在借助走格子实验理解“公倍数和最小公倍数”的基础上，教师还可以隐去棋盘纸中的数字，让学生找一找、画一画除了长为3厘米、宽2厘米的长方形以外的正方形，并且找出正方形的边长。在此基础上，学生很快知道正方形的边长必须是长方形长与宽的公倍数这样的知识。如果这张棋盘纸无限放大，那么能找到的正方形的个数就有无数个，也正对应“如果不限定公倍数的范围，两个数公倍数的个数是无限的”这样一个特征。这样的实验设计不仅让学生在“做数学”中，进一步理解抽象概念的意义，还渗透了数形结合的思想，提高了学生的数学学习能力。

【教学片段3】

师：刚才我们在棋盘上看到了数，现在能看到形吗？

生：我看到了一个个长方形。长是3厘米，宽是2厘米。

师：除了长方形，还能看到什么图形呢？请同学们拿出棋盘纸的反面，在上面找一找、画一画，并完成实验报告单（3）上面的内容。

师：你知道这个正方形的边长是几吗？

生：6。

师：为什么呢？

生：因为2×3=6，3×2=6。

师：6作为正方形的边长，能用今天学到的知识解释吗？

生：6是2和3的公倍数。

师：还有其他正方形吗？它的边长是多少？现在，你可以用一个更合适的词亮明12，18的“身份”吗？你觉得再这样围下去，围出的正方形边长是多少？这样的正方形围得完吗？（课件再演示）

通过这样的实验，学生不仅能将正方形存于想象中，还可以用“数”来把它们的共同点说出来。

三、让学生灵活运用数学概念，自主设计数学实验

“再创造”是数学教学方法的核心，应当被作为数学教育的一个教学法原则得以确立。实现“再创造”的前提是要把数学教育作为一个活动过程加以分析，在整个活动过程中，学生只有始终处于一种积极、创造的状态中，参与这个活动，感觉到创造的需要，才有可能进行“再创造”。

【教学片段4】

师：刚才我们通过单、双人走格子实验和拼格子实验，一起认识了公倍数和最小公倍数，想不想自己动手设计一个格子实验呢？

师：同桌两人先确定一个共同的格数，若想让两人共同跳进你们设定的这个格数，可以怎么设计游戏规则呢？请大家把你们的游戏规则和发现记录在实验报告单（4）上。

实验报告单（4）

实验内容：设计格子实验

实验目的：应用公倍数

实验步骤：

1.想一想：我们想共同走进（ ）这个格数。我们想到的数是（ ）和（ ）。

2.走一走：规则执子走数。

3.议一议：还能找到什么样的两个数也能同时走进设定的格数。

实验结论：我们发现，能同时走进（ ）这个格数的数有（ ）和（ ）。

师：想一想，在格子实验的操作中还有哪两个数也能走进这个格数呢？你还能找到其他不同的数吗？什么样的2个数都能走进你们设定的格数呢？

生：设定格数的因数。

师：这样的数可以找到多少对呢？请你们课后再去找一找。

教师应意识到，并非数学教材中的所有内容均可用来进行数学实验。确定内容后，教师要重视实验教学目标的设定，并准备实验器材和实验报告单。在整个实验过程中，教师应站在学生立场，遵循儿童的认知心理，准确把握学生实际动手操作能力的水平，让学生在学习活动中能真正地动起来，在“做”中体验，在“做”中学习，在“做”中思考，以达到助力学生素养提升的目的。

基于数学实验进行的概念性数学知识的教学，可以将抽象的数学概念性知识融入实验流程之中，让学生通过规范的实验流程操作，进行数学化分析。在观察、思考、交流和讨论的过程中，学生逐渐习得抽象的概念性数学知识，提升了综合能力。

参考文献：

［1］蒋敏杰.小学数学实验的内涵、价值与教学策略［J］.小学数学教育，2023（10）.

［2］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022.

（责任编辑：杨强）