基于问题驱动 培养关联思维

【摘 要】计算思维是设计计算系统的思维过程，它具有完整性、递进性和关联性等特点。在高中信息技术教学中，教师可基于问题驱动，将生活逻辑、学习逻辑和知识逻辑有机融合，让学生经历学习的起点关联、过程关联与结果关联等过程，找到真实的学习起点、经历真实的学习过程并拥有真实的学习收获，从而培养其计算思维。

【关键词】高中信息技术；问题驱动；关联思维；计算思维

【中图分类号】G633.67 【文献标志码】A 【文章编号】1005-6009（2024）27-0066-04

【作者简介】王卫全，江苏省淮安市教学研究室（江苏淮安，223001）信息科技教研员，高级教师。

《高中信息技术课程标准（2017年版2020年修订）》（以下简称“新课标”）指出，计算思维是运用计算机科学领域的思想方法，在形成问题解决方案过程中产生的一系列思维活动。从系统论的角度看，计算思维是设计计算系统的思维过程，具有完整性、递进性和关联性等特点。在这一过程中，如何实现问题的界定、分解、抽象、建模、算法的设计与实施、迭代与迁移等环节之间的深度关联？其关键是要具备关联思维。

一、关联思维的内涵

从系统论的角度讲，关联思维是建立系统要素之间联结的思维方式。关联主义理论对关联思维进行了阐述。关联主义理论是加拿大学者西门思根据数字时代知识无处不在的特点提出的学习方式，认为学习就是将学习网络中的不同节点连接起来的过程，其结果包括：节点的增加或减少，节点之间连接的增加、减少、加强或减弱，节点或连接的特性发生变化。因此，要促进持续性学习就要培育和维护节点之间的关系，实现节点之间的意义关联。关联主义理论将关联视为影响学习行为和学习效果的关键要素，直指学习的本质。综上所述，关联是知识与知识之间因为某种关系所建立的联系，这种联系既可以是纵向关联也可以是横向关联。学习者具备关联思维意味着能够将所学知识与认知结构中的已有知识和经验等建立关联，在关联中不断调整和丰富自己的认知结构，形成解决现实生活中真实问题的能力。

计算思维的发生离不开关联。计算思维是建立问题界定、分解、抽象、建模、算法设计、算法实施、迭代以及迁移之间关联的过程。问题界定是建立不确定性与确定性之间关联的过程，分解是建立模块与系统之间关联的过程，抽象是建立具体案例与概念之间关联的过程，建模是建立对象要素之间关联的过程，算法设计是建立指令之间关联的过程，算法实施是建立算法与代码之间关联的过程，迭代是建立新旧知识结构之间关联的过程，迁移是建立新情境与旧情境以及新概念与旧概念之间关联的过程。

二、问题驱动何以成为关联思维培养的操作路径

问题驱动教学包括三环节和五要素，从关联思维的视角看，问题驱动教学的三环节和五要素及其相互关系如下。

（一）从关联的视角理解三环节

问题驱动教学的三环节包括：创设情境，发现问题；分解问题，解决问题；回顾问题，知识建构。从关联的视角来看，每个环节内部关联，创设情境是发现问题的基础，发现问题是创设情境的目的；分解问题是为了解决问题，解决问题是分解问题的结果；回顾问题是知识建构的基础，知识建构是回顾问题的结果。三个环节之间相互关联，在结构上呈现“总—分—总”的特征，体现了发现问题、分解问题、解决问题和回顾问题的完整流程。

（二）从关联的视角理解教学五要素

教学五要素包含情境场、问题链、活动串、思维梯以及知识树，它们在问题驱动教学的过程中是连续发生的，学生学习的过程就是走进情境场、基于问题链、参与活动串、攀爬思维桥、建构知识树、迁移新情境的过程。相邻两个要素之间是相互关联的：一是情境与问题的关联，在体验情境场后，学生会产生认识冲突，然后发现核心问题；二是问题与活动的关联，通过活动解决问题，每个子问题对应相应的活动，问题链与活动串之间形成关联；三是活动与思维的关联，在活动中积累经验，通过对经验的反思，培养高阶思维；四是思维与知识的关联，思维是知识生成的过程，知识是思维进阶的结果。

（三）问题驱动与关联思维培养过程的关系

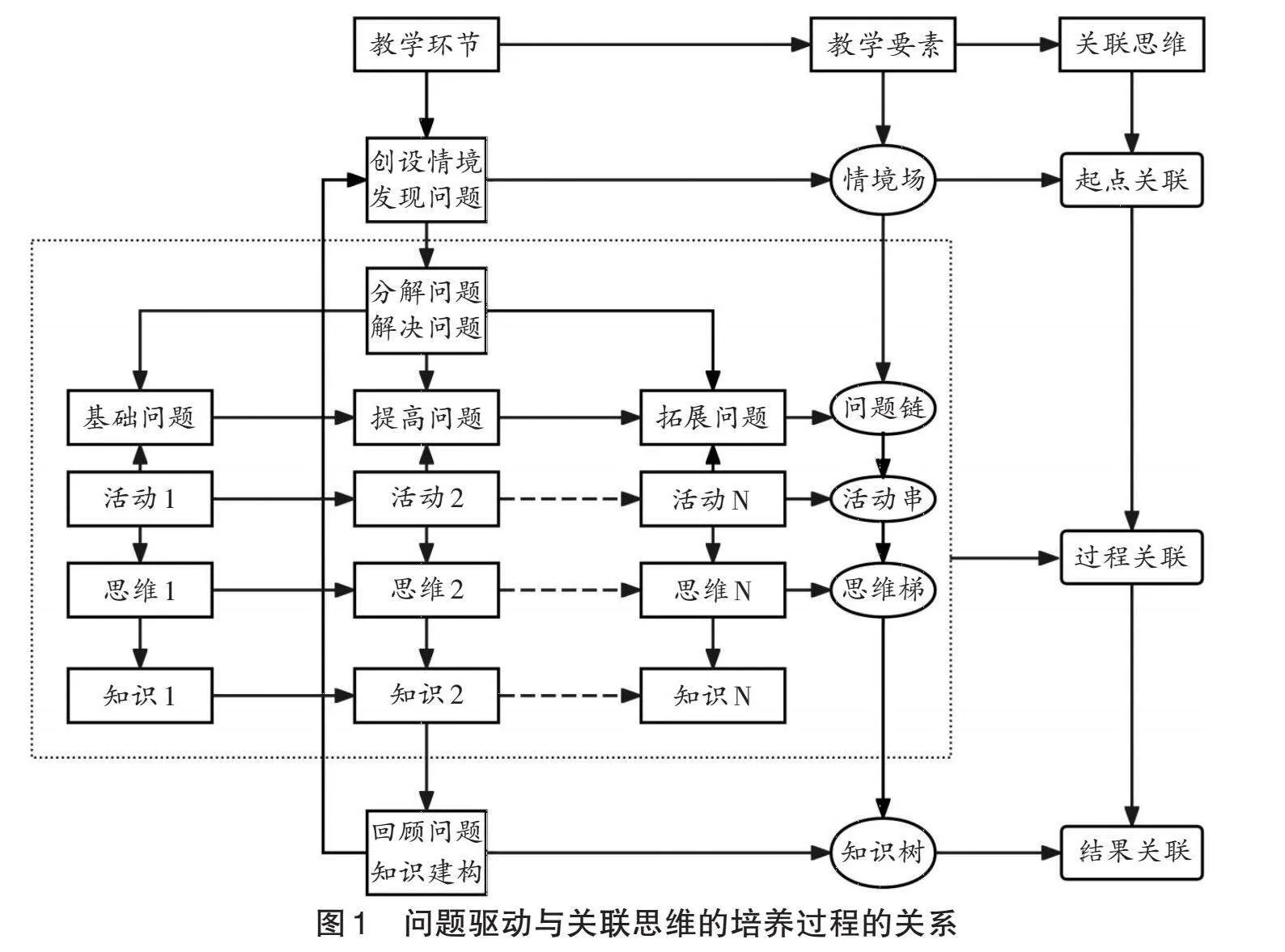
从系统论的角度讲，教学环节是教学系统的时间结构，而教学要素是教学系统的空间结构，两者共同构成教学的完整系统，通过关联思维实现起点关联、过程关联和结果关联，使计算思维的培养过程与关联思维的培养过程以及问题解决的过程保持一致性。因此，笔者构建如图1所示的关系图。

三、基于问题驱动的关联思维培养案例

（一）创设真实情境，建立起点关联

新课标强调真实性学习，学生的学习要从真实的生活或学习情境开始，促进学生学以致用，实现知识与生活的关联。教师在教学中创设审美情境，可以引导学生建立知识与审美生活的有机关联。

在课堂导入中，教师现场赋一首藏头诗，给学生学习的信心，突出学科育人的功能。随后，教师带领学生回忆并齐唱歌曲《早安，隆回》，相机引导“这节课就让我们一路同行，在汉诺塔游戏的过程中，共同经历一次愉快的递归之旅”。

（二）解决核心问题，经历过程关联

1.基于问题链，提供学习支架

（1）以核心问题指引学习方向

在创设情境、发现问题环节，教师安排学生观看自己录制的讲解演示汉诺塔移动的视频，引导学生发现并总结汉诺塔圆环的移动规则，思考手工移动64层汉诺塔圆环需要多长时间。学生猜测1年、2年或5年。当教师说出需要5800亿年时，全体学生发出惊讶的感叹，此时教师进一步追问：“如何用编程的方式模拟汉诺塔圆环的移动过程呢？”

整堂课围绕核心问题展开，将核心问题转化为学生可感知的学习目标，也是学习成果评价的依据，体现了逆向设计的思想。

（2）以子问题推进教学进程

教师将核心问题分解为五个子问题。问题1：如何手工移动1至3层汉诺塔？问题2：汉诺塔圆环移动有何规律？问题3：如何将递归模型转化为递归函数？问题4：如何将递归函数转化为递归算法？问题5：如何将递归算法转化为程序代码？

两个相邻的问题之间突出问题的转化，随着问题难度和开放度逐步加大，问题之间的关联深度和广度也逐步深入和扩大，从而有效推进教学进程。

2.参与活动串，完成活动任务

活动是为解决问题服务的，五个活动对应五个子问题，学生可通过自主实践、小组讨论等方式，建立不同学习方式之间、生生之间以及师生之间的关联。

（1）活动1：回忆视频中的移动过程，尝试移动手中的圆环，填写表格。

在活动1中，学生通过回忆视频中教师的示范移动过程，与自己的移动过程建立关联，寻找其相似点和不同点。

（2）活动2：分析圆环的移动过程，总结规律，填写表格。

在活动2中，通过分析圆环的移动过程，学生将操作过程进一步抽象，将过程符号化。教师给出1层汉诺塔圆环的移动过程与规律，作为支架，启发学生思考2层和n层汉诺塔圆环的移动过程和移动规律，从而建立不同层数汉诺塔圆环移动过程与规律之间的关联。

（3）活动3：回忆自定义函数的功能及格式，填写表格。

在活动3中，学生回忆自定义函数的功能及格式，建立递归函数与数学中自定义函数之间的关联；同时明确han（n，a，b，c）函数与移动模型“有n个圆环，从A柱通过B柱移动到C柱”之间的关联，以此递推，让学生明白递归函数的子函数就是在han（n，a，b，c）函数基础上的持续迭代。

（4）活动4：打开画程软件，设计算法，分析自动生成的代码（设计过程略）。

在活动4中，通过填写递归函数以完善算法，让递归算法在画程软件中运行，建立递归函数与算法的关联；通过分析自动生成的代码，建立算法与代码之间的关联。

（5）活动5：打开Python软件，完善程序代码。

教师引导学生输入不同层数，观察输出结果，并与手工移动过程进行比对。随后，教师引导学生思考如果计算64层汉诺塔圆环移动时间，计算机要运行多长时间。

在活动5中，通过与手工移动过程的对比，学生可以发现计算机解决问题的优势；通过对64层汉诺塔圆环移动时间的测算，指出现代计算机的不足，进而引导学生增强自主可控和原始创新的社会责任感，发挥学科的育人价值。

以上五个活动，基于学生的最近发展区，突出基础问题自主学习、提高问题合作学习和拓展问题探究学习的基本思路，强化了活动与问题以及活动与活动之间的关联，发挥了活动的学科实践价值。

3.攀爬思维梯，经历计算思维的过程

计算思维的培养过程是学生思维逐层抽象的过程，需要思维梯的帮助，从而实现思维进阶。其中，界定问题时需要发现思维，子问题1需要实践思维和符号思维；子问题2需要归纳思维与抽象思维；子问题3需要联想思维和整合思维；子问题4需要算法思维与创新思维；子问题5需要工程思维与迭代思维，分别对应了计算思维培养的全过程。

（三）知识建构迁移，达成结果关联

1.让学生经历知识的发生过程

知识的发生过程就是回到知识的起点。本节课中，教师引导学生从学科大概念算法开始，探求经典递归算法，从知识发生的视角去回答这一问题，取得了较好的学习效果。

2.让学生经历知识的发展过程

回顾知识的发展过程就是要让学生持续建构知识。以递归算法为主线，学生经历完整的关联过程：移动经验的积累—移动过程的记录—移动规律的发现—递归模型的建构—递归函数的创建—递归算法的设计—递归代码的编写—递归之美的发现—递归思维的迁移。

3.让学生经历知识的创造过程

一是要内化知识体系，形成自己的观点，以思维导图的形式呈现知识建构的结果。二是让学生经历知识的迁移过程，将程序编写中的递归迁移到生活中，将生活逻辑、学习逻辑与知识逻辑有机融合。

【参考文献】

［1］朱彩兰，陈彤，李艺，等.关联思维的内涵与形成路径研究［J］.电化教育研究，2023，44（5）：29-35，43.

［2］钟柏昌，刘晓凡.跨学科创新能力培养的学理机制与模式重构［J］.中国远程教育，2021（10）：29-38，77.