探理：在体验中发展数学思维

【摘 要】数学是思维的学科，数学知识的产生、发展、迁移和推广都需要经历严谨的探理。在初中数学体验教学中，学生在数学学习中经历困惑、冲突或者矛盾，遇到困境，然后经过操作、联想、对比、抽象、推理、反思、否定和重构等一系列探理过程，实现对数学知识由浅层的经验理解到深层的领悟觉知，在体验中发展数学的思维。

【关键词】初中数学；探理；数学体验；教学模式

【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009（2024）27-0017-05

【作者简介】1.张爱平，南京市金陵中学（南京，210005）副校长，正高级教师，江苏省数学特级教师；2.万涛，南京大学附属中学（南京，210008）教师，高级教师；3.吴涛，南京市红山初级中学（南京，210000）教师，一级教师；4.陈吉，南京市第二十九中学（南京，210029）初中部教师，高级教师。

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）指出，通过经历独立的数学思维过程，学生能够理解数学基本概念和法则的发生与发展，数学基本概念之间、数学与现实世界之间的联系……发展质疑问难的批判性思维，形成实事求是的科学态度，初步养成讲道理、有条理的思维品质，逐步形成理性精神。［1］

新课标指出了数学思维过程对于培养一个人的思维的重要性，学生学好数学的关键是通过探理，发展数学思维。数学体验教学是培养学生数学思维的重要载体，通过数学体验教学，学生在操作中思考，在思考中探理，在探理中觉悟。这样的体验教学能发展学生思维，对这样的体验教学模式的探索是有意义、有价值的。

一、探理的内涵和要义

1.探理的内涵

《新华字典》中对“探”和“理”的解释是“探”即寻求探索，“理”即道理、事物的规律。“探理”表示寻求探索道理和事物的规律。它是数学知识产生、发展、迁移和推广的重要途径。

2.探理的要义

探理主要是指从事实和命题出发，依据一定的规则推出其他命题或结论的思维过程。在初中数学体验教学中，探理侧重数学的逻辑推理，指通过逻辑推理，得到数学命题或结论。逻辑推理主要表现为：掌握推理基本形式和规则，发现问题和提出命题，探索和表达论证过程，理解命题体系，有逻辑地表达与交流。［2］逻辑推理主要包括两种类型：一类是从特殊到一般的推理，推理形式主要为归纳和类比；一类是从一般到特殊的推理，推理形式主要为演绎。因此，探理的要义主要体现在演绎推理、归纳推理和类比推理三种方式。

二、探理对发展数学思维的意义

从其内涵和要义出发，探理在发展学生数学思维方面具有重要意义。

首先，探理有助于学生运算能力和推理能力的提升。传统教学中，学生往往通过死记硬背来掌握数学运算和推理的步骤和法则，使得颇具思维含量的数学运算和推理变成机械的数字操作，这样不利于学生运算能力和推理能力的提升。而在体验教学中，教师引导学生通过操作体验、理解算理、逐步推理，在算理和算法之间，在探理和推理之间搭建桥梁，加深学生对运算和推理的理解。

其次，探理有助于学生积累数学活动经验。在探理过程中，学生通过观察、操作、分析、推理、归纳等活动，经历知识生成的过程，体验获得知识的喜悦，积累了数学活动经验。

最后，探理有助于学生感悟数学的严谨性，形成实事求是的科学态度与理性精神。学生经历独立的数学思维过程，能够理解数学基本概念和法则的发生和发展，理解数学基本概念之间、数学与现实世界之间的联系，分析、解决简单的数学问题和实际问题，经历数学“再发现”的过程。这样的“再发现”过程，有助于发展学生质疑问难的批判性思维，有助于学生逐步养成重论据、重逻辑的思维习惯，使其初步养成讲道理、有条理的思维品质，逐步形成理性精神。

三、以“探理”为体验意义的数学体验教学模式的框架

数学是思维的学科，思维的形成离不开探理。在数学体验教学过程中，要让学生的学习真正发生，探理是其中一个重要环节。在这个环节中，我们探索出以“探理”为体验意义的数学体验教学模式的框架：建构符号表征意义—建构经验关联—形成思维加工—形成思维跃迁—实现问题解决。

四、以“探理”为体验意义的数学体验教学模式的实施策略

在数学体验教学模式中，教师应通过创设有驱动性的问题情境，引导学生产生认知困惑，然后启发学生对原有知识进行经验关联，从而激活学生的已有经验；引导学生运用已有知识进行关联操作体验，启发学生进行逻辑推理验证等，使其通过探理解决自己的困惑、矛盾和冲突，实现问题解决，并对整个探理过程进行总结优化反思。因此，教师启发学生探理的实施策略为：创设问题情境—启发点拨激活—组织引导探究—完善补充升华；学生自主探理的实施策略为：激活已有经验—关联操作体验—逻辑推理验证—总结优化反思。

在义务教育阶段，数学思维主要表现为：运算能力、推理意识或推理能力。其中，运算能力重在代数探理，推理能力重在几何探理。运算能力指学生能够理解运算的算理，并能寻求合理简洁的运算方法来解决问题。推理能力主要培养学生的逻辑推理能力，逻辑推理能力是几何探理过程中必需的一种能力，培养学生几何探理的过程就是在提升学生逻辑推理能力。

下面，笔者分别从代数推理和几何推理的角度，通过案例具体阐释以“探理”为体验意义的数学体验教学模式的实施策略。

案例1：有无必胜方案

如图1，现有A、B、C、D四个长方体容器，A、B的底面积都为a2，高分别为a、b（a＞0，b＞0，a≠b），C、D的底面积都为b2，高分别为a、b。小明和小聪商定一种游戏规则：小明先从这四个容器中任取两个，剩下的给小聪，盛水多者获胜。请分析，无论a、b的大小关系，小明有无必胜的方案？若有，应取哪两个容器？若无，请说明理由。

【激活已有经验】学生首先会思考有6种选择，选择容器A和B，A和C，A和D，B和C，B和D，C和D，要计算盛水量，学生的已有经验就是计算每个容器的体积，因此会想到长方体的体积公式，从而激活学生的知识经验。

【关联操作体验】学生根据长方体的体积公式，得到容器A的体积为a3，容器B的体积为a2b，容器C的体积为ab2，容器D的体积为b3，这四个容器的体积哪个最大，哪个最小呢？根据条件a＞0，b＞0，a≠b，但a和b谁大谁小却不知道，因此无法判断哪个容器盛水多。

学生也会通过计算所选的两个容器的体积之和来进行比较，容器A和B的体积为a3 + a2b = a2（a + b），容器A和C的体积为a3 + ab2 = a（a2 + b2），容器A和D的体积为a3 + b3，容器B和C的体积为a2b + ab2 = ab（a + b），容器B和D的体积为a2b + b3 = b（a2 + b2），容器C和D的体积为ab2 + b3 = b2（a + b），但仍然无法判断哪个容器盛水多。在这里，学生的思维受阻，利用已有知识解决的方法行不通，遇到学习困境，渴望得到新的理解。

【逻辑推理验证】在教师的启发点拨、组织引导下，学生经过深层思考，发现比较两个代数式的大小可以用作差法来完成，然后对已有知识进行重构，经历由浅层的经验理解到深层的醒悟觉知的探理过程。

不妨设取A、B两个容器的盛水量为AB（其他类似），可得：

①AB - CD = （a + b）2（a - b）

②AC - BD = （a2 + b2）（a - b）

③AD - BC = （a - b）2（a + b）

因为a＞0，b＞0，a≠b，学生发现①中（a + b）2（a - b），②中（a2 + b2）（a - b），仍然无法判断正负，但在③中（a - b）2（a + b），无论a和b谁大谁小，（a - b）2（a + b）恒大于0，所以必胜方案是选择容器A和D。

【总结优化反思】从这个代数推理的问题中可以看出，学生所具备的知识是求长方体的体积，但是学生用公式表示出体积后，遇到学习困境：由于不知道a和b的大小，无法判断哪个容器的体积大，哪个容器的体积小。学生尝试把两个容器的体积加起来观察，发现还是不行，再次遇到困惑。这时教师适时启发点拨，并组织引导探究，学生发现比较两个代数式的大小可以用作差法，从而引导学生去完善解决这个问题。学生经历实践推理验证的探理过程，最终找到解决问题的方法，发展了其数学思维。

案例2：“圆周角”教学

“圆周角”是苏科版初中数学教材九年级上册第二章的内容。在圆中，圆周角与弦、弧和圆心角之间存在很多关联。很多教师都觉得“圆周角”这节课不好上，主要是因为没有弄明白圆周角从哪来，为什么要研究圆周角。要想上好这节课，教师必须想清楚两个问题。

问题1：在学习圆周角的定义时，“顶点在圆上”容易理解，如何才能使得学生自主归纳出“两边都和圆相交”这一特征？

问题2：在学习圆周角的性质时，学生怎样才能想到圆周角与圆心角的关系？

因此，下面笔者尝试借助圆周角体验仪（见图2）来开展体验教学，帮助学生深刻理解圆周角的概念和性质。

（1）发现圆周角

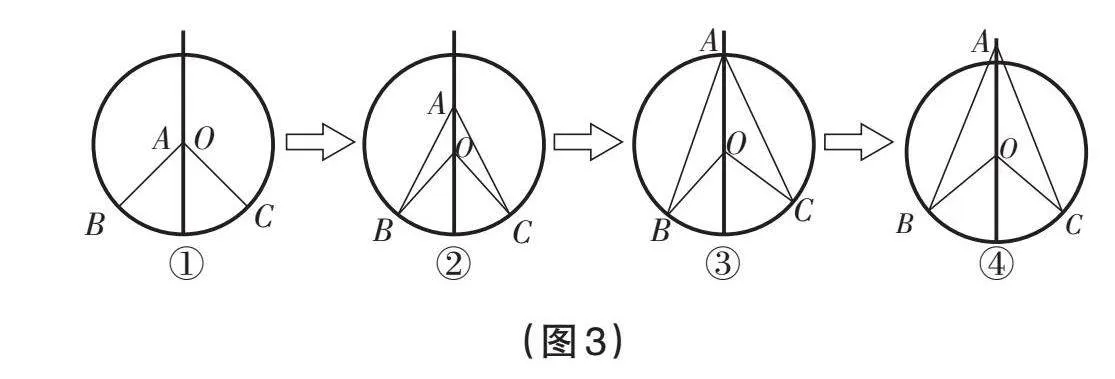
如图3，∠BOC为圆心角，让∠BAC的顶点A从圆心O出发，在直轨道上自由移动，在移动的过程中让学生感受∠BAC的大小随点A的位置变化而变化的规律：以点A从圆心O向上移动为例，在移动的过程中，点A离圆心O越远，∠BAC越小。

观察这些角的特征，根据点A位置的“不相同”，学生不难把点A的位置分为三类：圆内、圆上和圆外，进而把这些角分为三类：顶点在圆内的角、顶点在圆上的角和顶点在圆外的角。

学生对哪类角最感兴趣？心理学研究表明，人对变化过程中的某些特殊状态往往表现出特殊的兴趣。顶点在圆上的角是特殊状态，这必定是学生最感兴趣的角。自然地，学生发现了“圆周角”。

（2）探索圆周角的性质

问题：圆周角∠BAC的度数可能与什么有关？

【激活已有经验】学生通过观察和操作圆周角体验仪，发现与它所对的[BC]有关，学生根据已有经验，联想到圆心角∠BOC的度数等于[BC]的度数，圆周角∠BAC的度数可能与圆心角∠BOC的度数有关，猜想∠BAC = [12]∠BOC。

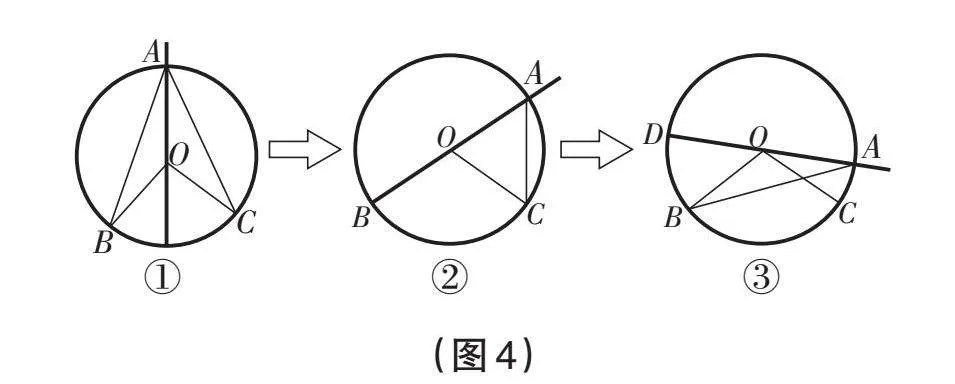
【关联操作体验】学生通过操作圆周角体验仪发现：当点A从圆心O出发，在直轨道上向上平移到圆上，此时∠BAC和∠BOC如图4中的①。学生根据外角的性质探理，得到∠BOC = ∠BAC + ∠B + ∠C，接着根据OA = OB = OC，得到∠BOC = 2∠BAC。

当点A沿着圆周移动，使得AB和OB重合时，如图4中的②。根据外角的性质得到∠BOC = ∠BAC+∠C。由于OA = OC，因此∠BAC = ∠C，即∠BOC = 2∠BAC。

当点A沿着圆周继续移动，当圆心在圆周角∠BAC外部的情形时，如图4中的③，此时，学生的思维受到阻碍，探理出现困难，学生遇到学习困境，不知道如何证明∠BOC = 2∠BAC。

【逻辑推理验证】学生通过操作圆周角体验仪发现：转动直轨道，使其和OA所在直线重合——即作直径AD（如图4③），学生经过探理发现图4③和其他两图有相似之处，可以把∠DOC和∠DOB看成外角，∠BOC=∠DOC-∠DOB=2∠DAC-2∠DAB=2（∠DAC-∠DAB）=2∠BAC，得以验证。

【总结优化反思】学生在寻找∠BOC和∠BAC的关系时，会出现思维的局限，只会对图4①进行探理。图4②和图4③中，点A的位置不同，证明的方法也是不同的，需要全面看待问题。当学生遇到图4③的情形时，由于没有连接直径，很多学生想不到如何添加辅助线进行探理，思维受到阻碍。该如何突破思维阻碍呢？这时借助圆周角体验仪的帮助，学生通过上述操作体验——转动直轨道，就能发现探理的突破口。学生通过体验，经历由浅层的经验理解到深层的醒悟觉知的探理过程，发展了自身的思维。

数学体验教学中教师要站得高、看得远、想得透，引导学生有疑、有思、有探、有悟、有得，对学生的探理给予支持和肯定，为学生学习数学树立信心。教师只有通过探理来发展学生的思维，学生才能获得成就感和满足感，才会将所学知识融入日常的学习和生活中，并对其进行创新，促进学习和生活走向深处，获得更多的意义。

【参考文献】

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022：5.

［2］李昌官.逻辑推理素养及其培养［J］.中学数学教学参考，2023（1）：10-13，18.