倡导深度学习 发展数学思维

［摘 要］在强调深度学习的今天，数学教学不能只满足于知识的讲授，还应重视学生数学思维能力的培养。教学中，教师要学会放慢节奏，鼓励学生去探索、实践、交流和反思，让学生通过深度学习理解知识的本质，领悟其中蕴含的数学思想方法，有效提升学生的数学学习品质。

［关键词］深度学习；数学思维能力；数学学习品质

数学教学其实质是数学思维活动的教学，培养学生思维能力是数学教学的一项重要任务。那么在小学数学教学中如何培养学生的思维能力呢？

一、放慢节奏，提升思考的长度

在日常教学中，部分教师为了追求速度常常压缩学生独立思考的时间，使得学生对知识的理解可能是片面的，甚至错误的，从而影响教学效果。其实，教学中教师应该适当地放慢节奏，给学生一些细思、深思的机会，让学生可以更全面、更深刻地理解知识，有效发展和提高思维能力。

案例1 “两位数加两位数的口算”教学片段

课始，教师先通过情境导入让学生列出算式：45+23；然后，预留时间让学生根据已学的竖式法给出答案；最后，教师让学生思考：“如果不用竖式计算，你会算吗？”

师：这个问题是个新问题，大家不要着急，先慢慢想一想，看看怎样口算呢？你能想到几种方法呢？

教师没有急着让学生回答，而是预留时间让学生独立思考，自主寻找解题的突破口。几分钟后，很多学生已经找到了计算方法，并跃跃欲试地想要表达了。

生1：可以先算40+20=60，再算5+3=8，最后算60+8=68。

师：是个不错的想法，把2个两位数拆成了整十数和一位数，先将2个整十数相加，再将2个个位数相加，最后计算2个数之和，三步完成了计算。你们还有其他方法吗？

生2：先算45+20=65，再算65+3=68。

师：哦，生2是把后面1个数拆成了整十数和一位数，这样用第1个加数加上整十数，然后再加1个一位数，两步得到了答案。

生3：先算45+3=48，再算45+20=68。

师：大家真厉害，给出了这么多的口算方法。分析以上方法，它们有什么相同点，又有什么不同之处呢？你认为怎么算更简便呢？

在探索“两位数加两位数的口算”的过程中，教师没有硬性地将自己认为的最优方案讲授给学生，而是放慢速度让学生去探索交流，并思考不同算法间的区别与联系，通过提升学生思考的长度，发展学生的数学思维能力。

从课堂反馈来看，适当地延长课堂上等待的时间使学生回答的平均时间、回答的准确性和主动性都有所提升，课堂氛围活跃。其实，很多时候学生理解和掌握的知识并不是教师“讲”明白的，而是学生“想”明白的。因此，教学中教师要“多等一会”，预留时间让学生“多想一会”，从而帮助学生养成深入思考的好习惯，发展和提升学生的数学思维能力。

二、适时提问，提升思考的宽度

在日常教学中，部分教师为了能够顺利完成课堂教学计划，在课堂上总是急于追求“标准答案”。殊不知，教师所呈现的“标准答案”可能并不是学生易于理解和接受的，这样虽然学生在练习时能够通过模仿和套用来解决相应的问题，但是因为探索过程的缺失可能难以帮助学生形成深刻的认识，不利于学生学习能力的提升。因此，在实际教学中，教师应该“多问一句”，引导学生自主寻找可能存在的不同解法，以此提升学生思考的宽度。

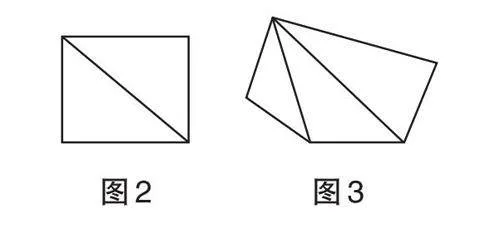
案例2 图1是由8个腰长为8分米的等腰直角三角形组成的装饰图，求装饰图案的面积。

问题给出后，教师让学生独立求解，大多数学生先算1个等腰三角形的面积，然后将结果乘以8，最终得到整个装饰图案的面积。教师点名让学生给出这个一般思路后，继续追问：“解决这个问题还可以怎么想？”问题给出后，学生尝试从其他角度思考，并给出了多种解题方法。

生1：2个等腰直角三角形可以拼出1个正方形，求出正方形的面积乘4可以得到整个图案的面积。

生2：还可以继续拼，4个小正方形可以拼出1个长是32分米、宽是8分米的长方形，这样求出长方形的面积就可以知晓整个图案的面积。

生3：4个小正方形还可以拼出1个边长是16分米的大正方形，大正方形的面积就是所求图案的面积。

以上看似习惯的一问，学生却给出了不同的解决方案。其实，在解决实际问题时，教师可以多问一句“还可以怎么想”，鼓励学生尝试从不同的角度思考，寻找不同解决问题的方法，以此拓展学生的思路。不过部分教师在教学中只追求结果，认为学生只要掌握一种解题方法，考试的时候不失分就可以了，没有必要将时间花费在多余的解法上，片面认为进一步思考和讨论就是浪费时间。长此以往，学生的思维会被禁锢，不利于学生求异思维和创新思维的生长与发展。同时，学生在学习中若不能多角度分析，会产生惰性思维，削弱积极情绪，影响自身思考灵活性的提升。如果教师能在解题后多问一句“还可以怎么想”，可能会收获许多意外惊喜，其效果远远大于多做几道题以及多给出几种解题方法。

此外，学生给出解题过程时，教师应多问一句“你是怎么想的”，旨在通过展示学生的思维过程帮助学生梳理解决问题的思路，有效避免学生简单机械地套用，让学生做到真懂、真会，有效提高学习能力。总之，教师在组织教学活动时应从教学实际出发，适时地多问一句，以此引发学生更深层的思考，提高学生的数学思维能力。

三、探寻本质，提升思考的深度

数学教学除了讲授数学知识，还要重视渗透数学思想方法，引导学生探索知识的本质内涵，让学生学会学习。教师要引导学生真正地把握数学知识的本质内涵，发现数学知识背后蕴含的数学思想方法，在教学中不满足于单一的“讲授”，应留给学生一些时间和空间让学生去思考与感悟，引导学生在解决原有问题的基础上“跳一跳”，以此提高学生自主探究能力和数学思维能力。

案例3 “多边形的内角和”主题活动

教学中，教师在原有探寻三角形内角和的基础上，通过师生互动交流推导出多边形内角和公式（n-2）×180°。结论给出后，教师并没有给出相应的练习让学生巩固强化，而是引导学生进一步探索公式中蕴含的秘密。

师：公式中之所以是“n-2”，是因为分成的三角形的个数比多边形的边数少2，为什么会这样呢？（学生沉思）

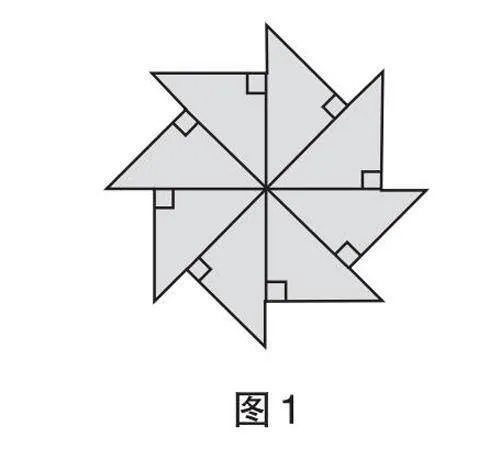
生1：我们可以从四边形开始研究。如果将图2中的四边形分成三角形，并使其原来的内角和不变，只要画1条“分割线”就能将四边形分成2个三角形。

生2：非常赞成生1的说法，我们还可以继续研究。如图3中的五边形，若将它分成三角形并使其内角和不变，可以从顶点出发，与不相邻的两点相连，得到2条“分割线”，将五边形分成3个三角形。

师：一定要与不相邻的两点相连吗？（教师看还有学生不知所以然，试图通过进一步追问消除学生的困惑）

生3：一定是不相邻的，如果是相邻的两点就不能达到“分三角形”的效果。

师：大家说得都非常好。通过以上分析，你们发现了什么？

生4：其实研究多边形的内角和就是研究这个多边形能够分成几个三角形。将1个多边形分成几个三角形，若使其内角和不变，就是从1个顶点出发，与不相邻的顶点相连。除去相邻的2个顶点，三角形的个数也就是比顶点数（边数）少2，因此多边形内角和公式（n-2）×180°。

在数学教学中，教师不仅要让学生“知其然”，还要引导学生通过深度思考“其所以然”，使学生在获得知识的同时掌握数学研究方法，促进其知识的深化。在日常教学中，当推导出公式、定理、法则后，教师不要急于让学生去解题，应该多让学生思考“为什么”，引导学生再往前走一步，这样学生离知识的本质就会更近一些，对知识的理解也更加深刻。

其实，学生的潜能是无限的，教师要相信学生、尊重学生，预留一定的时间和空间让学生去思考、去探寻，去追寻问题的本质，以此提高学生的数学学习品质，让学生实现知识的融会贯通。

总之，若想让学生深刻地理解知识，并能灵活地应用相关知识解决问题，教师就要“多等一会”“多问一句”，预留时间和空间让学生去探索、思考、感悟，从而通过深度学习发展和提升学生的数学思维能力。