基于说理能力培养的高中数学教学策略探讨

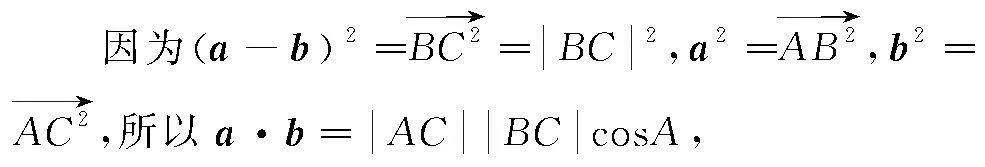
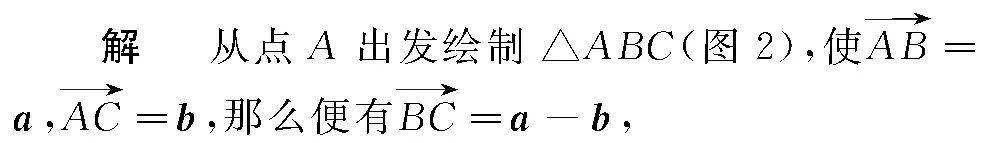
【摘要】本文以转变学生浅层学习状态，驱动学生思维品质进阶为导向目标，对高中数学教学提出指向学生说理能力培养的创新策略.首先，对说理能力的内涵进行基本介绍；其次，以案例分析的方式探讨从引导学生想“说理”、启发学生会“说理”、激发学生善“说理”三个角度上培养学生数学说理能力的路径方法.以期通过对学生的诱发、启发与激发，切实增进学生的数学学习参与积极性，更好地提升高中数学教学有效性.

【关键词】说理能力；高中数学；课堂教学

导致高中学生易在数学学习过程中出现低效学习问题的主要原因在于：学生对数学学习存在较大的抵触情绪，无法深刻把握数学学科的本质内涵.因此，为让学生的数学学习状态、学习方式得到有效调整，当前一线

教师应采取恰当可行的教学手段对高中数学教学形式进行精准优化，加深学生的数学学习感知体悟.鉴于此，本文以培养学生数学说理能力为出发点，对优化革新高中数学教学的方式方法展开探究.

1 数学说理能力的实质内涵

数学说理能力，顾名思义就是一种能够将数学原理、道理、理由以语言表达的方式呈现出来的数学学习能力，核心在于学生数学语言与数学思维的发展进阶[1].相较于义务教育阶段学生所需形成的数学说理能力，高中学生的数学说理能力主要体现在数学本质内涵的揭示、数学思想方法的解释、数学解题过程的表述三个方面.由此可见，数学说理能力的培养要点在于促进学生数学学习“学、思、悟、达”的深度结合.因此，在高中数学教学中对学生的说理能力进行针对性培养，不仅是提升学生数学学习效果的有效手段，同时也是塑造学生数学学习品格、发展学生数学学习能力的关键途径之一.

2 基于说理能力培养的高中数学教学策略

2.1 精创教学情境，调动积极情绪，诱发学生想“说理”

兴趣对学生学习方式、学习状态所起到的影响是有目共睹的[3].在高中数学教学中培养学生数学说理能力，教师便可有效借助兴趣的积极影响，通过创设契合高中学生喜好的直观教学情境的方式调动学生数学说理的热情，促使学生在愿意“说”、想要“说”、主动“说”中萌生数学说理意识.

例如 在教学湘教版高中数学教材必修第一册“集合的包含关系”一课时，高中数学教师便可从学生生活实际出发，创设符合学生认知的教学情境，引发学生的数学说理兴趣，激发学生的数学说理意识.

首先，为学生讲述战国时期逻辑学家公孙龙的“白马非马”论，为学生创设故事教学情境，并鼓励学生尝试迁移运用已知的数学知识转译这一哲学命题，激发学生的数学说理兴趣.由此，公孙龙的“白马非马”论便可表示为：白马是马，白马∈马；黑马是马，黑马=马；所以白马≠马.由此，学生便会认清公孙龙“白马非马”论中的诡辩在于将“是”的概念模糊化，为其赋予了三层概念.第一，将“是”表示为了“=”，如，黑马是马，黑马=马；第二，将“是”表示为了集合与元素之间的归属关系，如，白马是马，白马∈马；第三，将“是”表示为了集合与集合之间的包含关系，如，白马不包含于黑马，所以白马不是马，即白马马.在此之后，高中数学教师便可以提问“那么你们能够用正确的逻辑观点反驳公孙龙‘白马非马’这一诡辩吗？”激发学生学习数学的兴趣，高效、流畅地导入课程，引领学生学习本课新知，提升学生对本课知识的吸收效率.

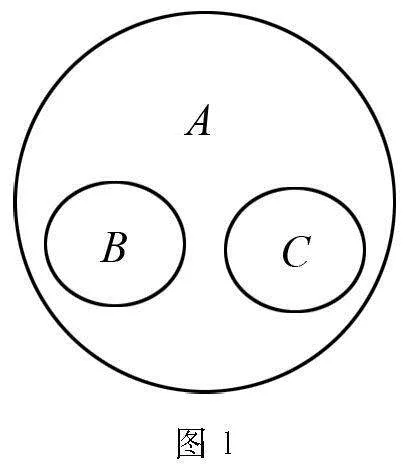
其次，在引领学生学习集合的子集与真子集、集合的交与并等知识内容时，则可由学生的校园生活出发，引领学生将整个班级视作集合A，班级内男性学生视为集合B，班级内女性学生视为集合C，并鼓励学生用Venn图进行数学说理.由此，学生便会主动结合自身生活经验，在直观图示说理中厘清集合与集合之间的关系，得到数学学习效率的提升.

说理1：集合B（班级内男性学生）中任意一个元素都是集合A（整个班级）的元素，用Venn图表

说理2：班级内学生既属于集合A，同时又属于集合B，所以班级内学生是A与B的交集，记作A∩B.

说理3：集合B与集合C组成了整个班集体，所以集合A是集合B与C的并集，记作B∪C.

在学生根据班级男女生情况利用集合知识进行自主说理时，高中数学教师还可鼓励学生针对其他人的说理观点与过程方法提出不同见解与思路，以此来有效促进学生的思维碰撞，让学生在相互指正中实现有机互动，进而更好地厘清数学说理逻辑，全面把握集合与集合之间的内在联系.

最后，在引领学生进行集合推理时，教师则可让学生利用本课所学反驳公孙龙的诡辩，从而在有效激发调动学生数学说理兴致与积极性的同时，让学生在推理、反证、转换中更好把握用必要条件与充要条件推理集合之间关系的方式方法，进而在“学思悟达”的交融中提升数学学习效率与数学逻辑思维能力.

在高中数学教学中培养学生数学说理能力时，结合实际教学内容为学生创设多元化的教学情境，驱动学生围绕具体情境展开数学说理，不但有利于学生说理意识、说理兴趣的激发调动，而且学生在有条理、有逻辑地进行数学说理时，其对数学知识内容的感知体悟也会在潜移默化之中得到升华，数学学习效率与数学说理能力自然会因此而得到稳定提升[4].

2.2 设置核心问题，厘清思维脉络，启发学生会“说理”

数学说理是一项数学语言与数学思维密切配合的综合性学习活动.因此，在高中数学教学中培养学生数学说理能力时，教师除了要通过创设多元情境诱发学生说理兴趣，激活学生数学说理意识外，同时也要通过设置有效的核心教学问题为学生搭建思维能力进阶的“阶梯”与“支架”，以此来确保学生能够在数学说理中把握到数学知识、数学问题的核心本质，实现条理清晰、逻辑严谨的数学说理[5].

核心问题1：对于任意两个数a与b，有哪些乘法公式？那么，对于任意两个向量a与b，是否同样也有类似的公式？这些公式对向量是否成立？

核心问题2：如果想要看乘法公式对向量是否成立，那么乘法公式是如何成立的呢？

核心问题3：探索向量等式向量a－b2=a2－2a·b+b2的几何意义，可以构建什么几何图形？构建这一几何图形可以根据什么？

由此，学生便会在教师所设置的核心问题引导与启发下自觉展开由浅入深的数学说理.

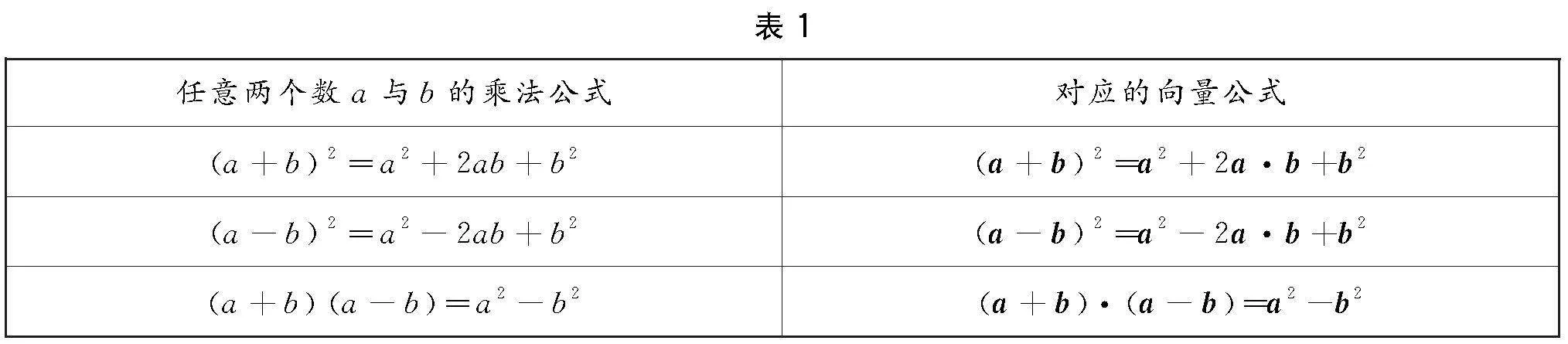
首先，根据核心问题1罗列a与b的乘法公式，并初步构建相对应的向量公式（如表1）.

其次，根据核心问题2探索乘法公式成立的原理.

乘法公式a+b2=a2+2ab+b2成立原理的探索：a+b2=a+ba+b=aa+b+ba+b（加乘分配律）=aa+ab+ab+bb（乘法交换律，加法结合律）=a2+2ab+b2.根据这一乘法公式成立的原理，便可推导出相对应向量公式a+b2= a2+2a·b+ b2成立.同理，其余两个向量公式a－b2= a2－2a·b+b2，a+b·a－b=a2－b2也同样成立.

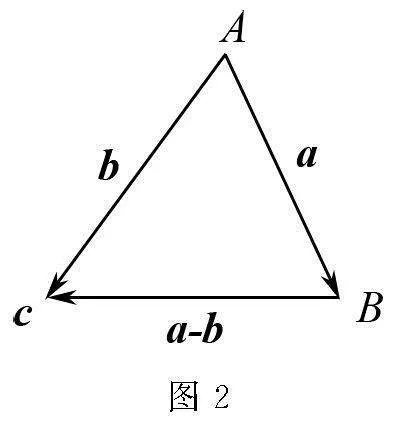
最后，根据核心问题3构建对应向量等式a－b2= a2－2a·b+b2的几何图形.联系已知数学几何知识学习经验，可得到边与边之间存在平方关系的图形主要有三角形.由此，便可构建三角形探索这一等式的几何意义：

所以向量等式a－b2=a2－2a·b+b2的几何意义便是△ABC中三边长及其内角A的余弦关系，是三角形余弦定理.

以问题激活学生思维，让学生在思考问题、探索问题的过程中梳理数学说理逻辑，理清数学说理思维脉络，不仅能够让学生更加自觉地联系已知，在温故知新中掌握数学说理技巧与方式方法，学生在进行数学说理的过程中，其对数学知识之间所存在的内在关联、紧密逻辑也会形成更为深刻的记忆，进而实现真正意义上的有效学习、深入探究、深刻思考.

2.3 开发错题价值，注重逆向思考，激发学生善“说理”

数学说理能力关注的是学生思维品质的进阶提升.因此，在高中数学教学中培养学生数学说理能力时，教师同样也要重视起学生说理方向的调整，通过刻意出示错题的方式激发学生的思维矛盾与认知冲突，让学生在剖析、纠正错误的过程中得到思维定式问题的突破，学会从正向、逆向等多个角度上进行数学说理.

例如 在教学湘教版高中数学教材必修第四册“等差数列”一课时，高中数学教师便可在学生把握求等差数列公差与某项数的方法技巧后，为学生布置相关数列练习题.并在每个学生完成随堂数学练习后，将学生的错题整合起来呈现给学生，鼓励学生从逆向的角度上进行数学说理，分析错题的成因、解题思路及过程中所存在的问题，并做出正确、有效的错题纠正.

由此一来，学生便会在指正错题问题、分析错题成因的过程中得到逆向思维与数学说理能力的锻炼强化，数学学习问题与数列求解误区等限制学生数学学习效率提升的因素也会以“润物细无声”的方式得到切实清除.

3 结语

总而言之，在高中数学教学中培养学生的说理能力，在某种意味上便是一种让学生深入参与数学课堂、全面投入数学探究的“迂回战术”.因此，高中数学教师在实际的教学实践中，培养学生这一数学学习能力时，便要从了解把握学生学习兴趣生成点、思维启动点入手，采取更为有效、合理的方式方法诱发、启发、激发学生数学说理的积极性与主动性，以此来切实改善学生“学、思、悟、达”分离问题，提高学生数学学习成效.

参考文献：

[1]曹庆安.说理是小学数学教学的必然追求[J].新课程导学，2022（31）：50-52.

[2]叶宝玉.三个节点，把握学生说理能力培养的契机时机——以《平行四边形的面积》教学为例[J].教育艺术，2022（08）：55-56.

[3]郭昭鹏.解剖几何题，构建“学习支架”，提高几何说理能力[J].初中生辅导，2022（13）：70-72.

[4]陈萍萍.思维可“说”，分析有“理”——构建小学数学高效“说理”课堂[J].教育界，2021（35）：41-42.

[5]王爱萍.和乐课堂，“理”在其中——探析如何构建趣味小学数学课堂培养学生说理能力[J].读写算，2021（06）：171-172.