发展型教育与中职数学分层教学有机结合案例分析

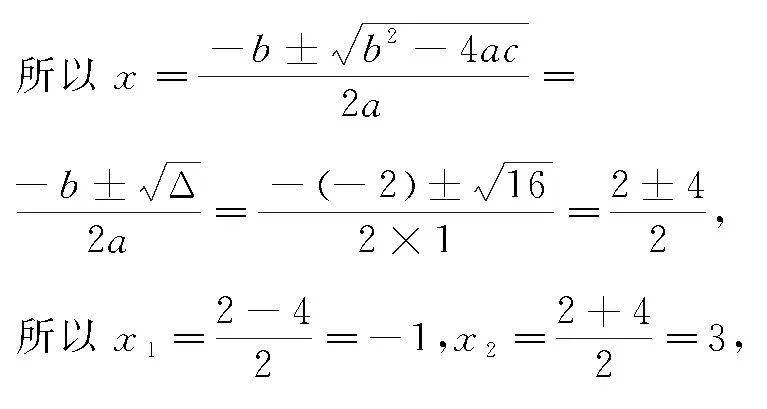
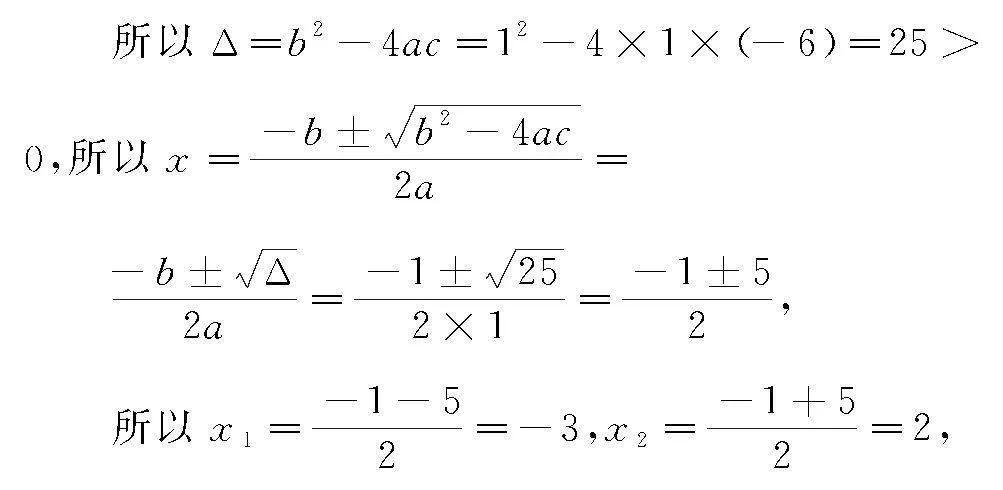
【摘要】本文以中职数学“一元二次不等式的解法”分层教学为例，研究将发展型教育与中职数学分层教学相结合的必要性.在推进素质教育深化改革的背景下，我们要对学生的个体差异及发展予以重视，使学生的潜能得以发挥.通过将发展型教育与分层教学相结合，可以提高中职数学教学的针对性和实效性，促进学生的全面发展.

【关键词】中职数学；分层教学；一元二次不等式

1 引言

如何科学有效地将发展型教育与中职数学分层教学相结合？如何通过这种结合提高学生的学习成绩、培养学生的兴趣爱好、促进社交关系等？针对这些问题，我们在多年的中职数学教学实践中，通过优化分层教学策略和发展型教育实施方案，可以实现两者的有机融合，提高教学质量和促进学生的全面发展.

2 案例分析

2.1 如何分层

首先，综合学生的学习态度、学习习惯、学习能力、知识结构等，即按照每个学生的课堂表现、学习兴趣、作业完成度、测试结果等因素进行分层.其次，在分层的基础上编成Ａ（优良型）、Ｂ（达标型）、Ｃ（困难型）三个层次，以便更好地针对不同层次的学生进行教学，促进他们的学习进步.本文以“一元二次不等式的解法”为例，例析如何将发展型教育与中职数学分层教学有机结合.

2.2 教材分析

本课内容选自高教版，中等职业教育课程改革国家规划新教材《数学》基础模块上册第二章的2.3.1节的第一、第二课时，主要学习一元二次不等式ax2+bx+c>0≥0或ax2+bx+c<0≤0，其中a≠0的解法.

2.3 教法分析

本课程采用混合式教学法，借助智慧课堂平台创设实时交互网络环境，线上线下教学相结合，以学生为中心，以微课自学法、问题导向法、任务驱动法、情境教学法为依托，着重在口诀的引入与理解，练习量的分层提高，以及练习方式的多样化上使用信息技术手段，创设具体的、直观的、有效的教学情境，以培养学生独立自学的能力，以及提升研究性学习和团队互助学习的能力，突出“做中学，做中教，做中求进步”的活教育思想.突破本章节重难点的关键是学会利用口诀模仿做题和做好笔记.

若一元二次不等式ax2+bx+c>0≥0或ax2+bx+c<0≤0，其中a≠0，其对应方程ax2+bx+c=0a≠0有实数根x1、x2x1<x2，则可用以下口诀写出一元二次不等式的解集：

（1）不等式ax2+bx+c>0≥0的解集是xx<x1或x>x2xx≤x1或x≥x2，口诀：大于取两边，小于小根或者大于大根.

（2）不等式ax2+bx+c<0≤0的解集是xx1<x<x2xx1≤x≤x2，口诀：小于取中间，按照“从左到右、由小到大”的顺序.

2.4 学情分析

我们发现学生似乎都忘了关于初中的解方程和解一元一次不等式等知识，而且计算能力相对薄弱，对于学习新知识的过程，还分不清哪个是大于、哪个是小于，再次给学生教授口诀“开口向谁，谁就大”，这样学生就能较好地分清楚大于、小于了.

2.5 学法分析

本章节内容，我们要学会观察—分析—讨论—化归—理解—应用.体会发展型教育与分层教学有机结合的重要性，还要学会发现法、模仿法等研究的基本方法.

另外，想要掌握好一元二次不等式的解法，必须记忆理解和加强训练.暂时的模仿，多数学生可以做到，但隔了一段时间基础弱的学生可能就忘得一干二净，因此复习很重要.

2.6 分层教学过程

2.6.1 面向全体学生，让C层生能依葫芦画瓢地掌握最基本的解题方法和步骤

在“一元二次不等式解法”的分层教学中，顾及全体学生的情况下，重点放在关注C层生的认知和接受上，引导学生用初中学习的求根公式法来解一元二次不等式.方法步骤如下：

请看例题解析：

例1 求下列不等式的解集：

（1）x2－2x－3≤0；

（2）x2+x－6>0.

解 （1）因为在不等式x2－2x－3≤0的对应方程x2－2x－3=0中，a=1，b=－2，c=－3，

所以Δ=b2－4ac=－22－4×1×－3=16>0，

所以根据口诀“小于取中间，按照‘从左到右、由小到大’的顺序”得一元二次不等式x2－2x－3≤0的解集为x－1≤x≤3.

（2）因为在不等式x2+x－6>0的对应方程x2+x－6=0中，a=1，b=1，c=－6，

所以根据口诀“大于取两边，小于小根或者大于大根”得一元二次不等式x2+x－6>0的解集为xx<－3或x>2.

2.6.2 由易到难，以提升C层生，发展B层生

为增强C层生学习效果，促进B层学生发展，由易到难，重点讲授如何运用因式分解法来解一元二次不等式.方法步骤如下：

将题目中的一元二次不等式整理为一般形式，确保不等式左端为一元二次式，右端为0，且二次项系数为正，即ax2+bx+c>0≥0或ax2+bx+c<0≤0，其中a≠0，然后写出对应方程ax2+bx+c=0a≠0，将方程左边的二次三项式进行因式分解，求出对应方程的根，最后根据口诀下结论，即可得到原一元二次不等式的解集.

请看例题解析：

例2 求下列不等式的解集：

（1）－2x>－x2+3；

（2）x2+x<6.

解 （1）将原不等式－2x>－x2+3化为一般式得：x2－2x－3>0，

其对应方程为x2－2x－3=0，

因式分解得：x+1x－3=0，

即：x+1=0，或者x－3=0，

则对应方程x2－2x－3=0的实数根为x1=－1，x2=3，

所以根据口诀“大于取两边，小于小根或者大于大根”得原不等式－2x>－x2+3的解集为xx<－1或x>3.

（2）将原不等式x2+x<6化为一般式得：x2+x－6<0，

其对应方程为x2+x－6=0，

因式分解得：x+3x－2=0，

即：x+3=0，或者x－2=0，

则对应方程x2+x－6=0的实数根为x1=－3，x2=2，

所以根据口诀“小于取中间，按照‘从左到右、由小到大’的顺序”得原不等式x2+x<6的解集为x－3<x<2.

2.6.3 梯级提升知识难度，以提升B层生，发展A层生

为了满足A层学生对知识发展的需求，确保他们能够“充分吸收”，同时提高B层学生的学习水平，我们在本节课后半段的教学中特意提高了知识的难度，从广度和深度上丰富了数学知识.方法步骤如下：

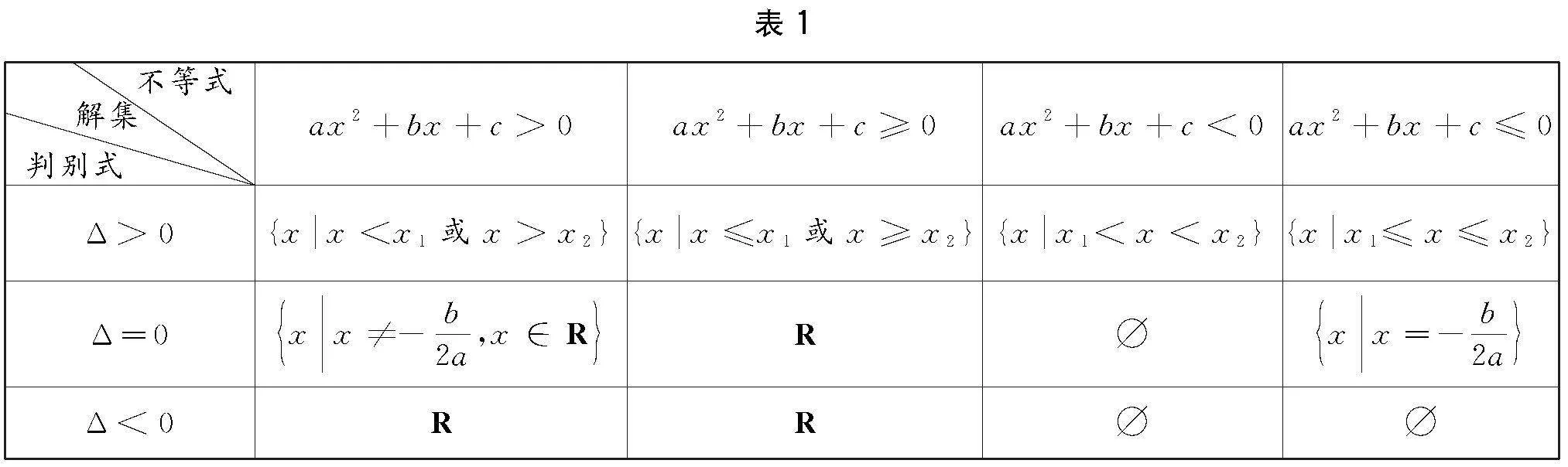
用二次函数图象解一元二次不等式.若方程ax2+bx+c=0a>0有实数根x1，x2x1<x2，则一元二次不等式ax2+bx+c>0≥0或ax2+bx+c<0≤0的解集表1所示：

使用这种方法解题，有助于促进初高中知识的衔接，以便实现从初中知识向中职知识的过渡，让C层生进一步掌握解题的方法和技巧.而这种教学方法主要还是面向B层和A层学生，旨在帮助他们更熟练地运用所学知识从多个角度去解题.

3 课堂练习和课外作业的安排

在中职数学分层教学中，我们不仅体现在教学行为上“分层”，课堂练习和课外作业的布置也应充分体现“分层”这一理念.根据学生不同层次的知识水平及其所能承受的程度，在难度和数量上有所区别，以便学生能够保质保量地完成作业并达到巩固和提高的目的.

4 结语

从案例分析可知，发展型教育与中职数学分层教学有机结合，能有效地将学生调动参与到课堂教学活动中，实现了全方位、全程、全员“三全育人”的教育目标.我们将“教”与“学”紧密地融合，让理论学习与实践应用有机结合起来，从而使学生能够更全面地发展.诠释“数学文化”，使师生成为数学文化的传播者与践行者.主要体现在以下几个方面：（1）尊重学生的个体差异：通过分层教学，每个学生都能在适合自己的学习环境中得到最大的发展.（2）挖掘学生的潜能：发展型教育注重培养学生的潜能和创造力，使得学生能够在数学学习中找到自己的优势和兴趣点.（3）提高学生的综合素质：这种结合不仅可以帮助学生掌握数学知识，还有利于培养学生的团队协作能力和社交技能.