加强变式教学，突破学生数学思维障碍

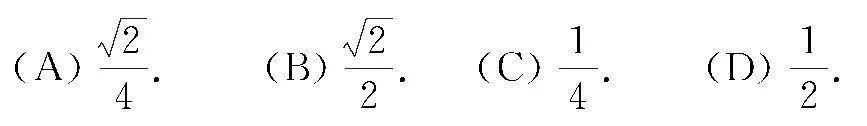
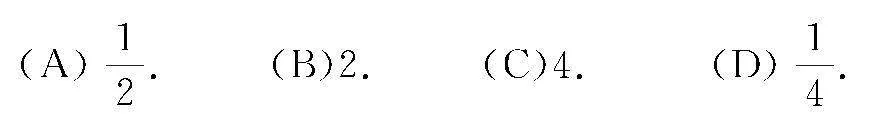
【摘要】加强变式教学对克服学生数学思维障碍具有积极的作用.首先，对思维障碍进行了定义和分类，并分析了其成因.随后，介绍了变式教学的基本原理和对学生思维发展的影响，重点阐述了其在克服思维障碍方面的应用.为进一步提高变式教学效果，还针对不同类型思维障碍研究了相应的变式教学策略，具体阐述了加强变式教学的方法和手段.最后，通过实证研究得出结论：加强变式教学可以有效地帮助学生克服数学思维障碍，提高其数学核心素养.

【关键词】数学思维；障碍；变式教学；实证研究

数学思维是指以数学的方式进行思考和解决问题的能力.它涉及对问题的分析、抽象、建模、推理和创新等过程.它要求思考者能够准确把握问题的本质，构建适当的数学模型，并通过推理和演绎等方法进行推导和解决问题.数学思维是一种基础性和普遍性的思维能力，在解决实际问题、科学研究、职业发展等方面都起到重要的作用[1].因此，培养和加强数学思维对于提高个人的综合素养和核心竞争力具有重要意义.但是，学生在数学学习过程中经常会遇到课上听得很清楚，课下在解决问题时却无从下手的囧象，究其原因主要是：对基本概念的理解不透彻，从而导致了数学思维定势的思维障碍；过度死记硬背没有深入理解其背后的数学原理和思想，从而导致的数学思维肤浅的思维障碍.

变式教学是一种以培养学生数学思维为目标的教学方法，主要通过以问题为中心、重视学生思考过程、鼓励学生自主探究等方式提高学生的数学思维水平.教学中教师有目的地设置从“变”的情境中发现“不变”的本质，从“不变”中探求规律.让学生明确问题的本质，以本质为主线，从不同角度、不同层面加以探究，加深对问题本质的理解，练就学生慧眼洞察的本领.变式教学不仅能加深问题本质的理解和掌握，更重要的是在激发学生学习兴趣，发展学生思维，培养和提高学生的数学素养方面有其独特的魅力.因此，加强变式教学的研究对提高学生数学能力、促进数学教育的可持续发展具有重要意义[2].

1 数学思维障碍的定义与表现

1.1 数学思维障碍的概念

数学思维障碍是指学生在数学学习过程中，出现了一系列的困难和障碍，阻碍了学生利用数学知识解决数学问题的步伐，使学生难以掌握数学技能，限制了学生解决数学问题的能力.这些困难主要来自教师的教学方法、学生的学习动力、学生家庭环境、个体差异等方面，集中表现为概念理解不透、死记硬背、记忆短暂、数学焦虑等不同形式[3].

1.2 数学思维障碍的主要表现

数学思维障碍主要表现为：对概念理解不透，对于某些数学概念的理解存在盲区或者误区，无法准确理解其含义和应用，从而导致了数学思维的定势性；死记硬背照搬硬套，仅仅通过死记硬背公式、定理等方式来掌握数学知识，缺乏深入理解知识的生成过程.

2 变式教学在突破数学思维障碍中的作用

2.1 变式教学

变式教学是一种以开发学生的创造力和创新能力为核心，以多样性和差异性为特点的教学方法.所谓“变式”，是指教师有目的、有计划地对命题进行合理的转化，不断更换命题中的非本质特征；通过配置实际应用的各种环境变换问题中的条件或结论，但应保留好对象中的本质因素，从而使学生掌握数学对象的本质属性[4].

2.2 变式教学在突破学生数学思维方面的应用

变式教学与传统教学方式的不同在于，它不仅关注知识的传授，同时也注重学生的思考能力、创新能力等多方面能力的培养，变式教学在突破学生数学思维方面具有无可替代的作用，主要体现在：一是提高概念理解能力，通过多种类型的问题和情境，帮助学生深入理解数学概念，在实践中增强对概念本质的认知.二是培养创造性思维，通过提供不同类型的数学问题，鼓励学生动手探索，寻找解决问题的创新方法和策略，提高学生创造性思维能力.三是强化记忆效果，变式教学涉及的问题类型、情境、方法等多种变化，使得学生需要运用不同的思维方式来解决问题，从而提高记忆效果.四是减轻数学焦虑情绪：变式教学注重学生参与度和自主性，让学生在轻松愉悦的氛围中学习，减轻数学焦虑情绪.

3 变式教学的策略和方法

变式教学的最终目标是为了突破学生的数学思维障碍，采取“先思后导，变式拓宽”的数学课堂教学模式，旨在培养学生的数学思维.因此，变式教学的策略和方法的选择必须充分考虑不同学生的个体差异性，通过采用不同的教学方式、教材、评价工具等措施，为学生提供更加个性化、差异化的学习体验，以达到更好的教学效果[5].根据学生的思维障碍表现，采取的变式教学的策略主要有以下几种.

3.1 加强概念变式，凸显概念本质内涵

数学教学的最终目的是要完善知识结构，强化知识体系，学生要明白各个知识点的形成过程.同时，通过串联相关知识间的联系，连点成线，连线成面，完成知识重组，完善知识结构，即明确各个知识的内涵和外延.而所有知识形成的起点与核心是概念，概念是人们认识事物最基本的成分，也是掌握知识的重要环节.概念变式是指变换定义陈述方式，从而加深概念理解的方法，明确概念的内涵与外延.把数学概念的抽象性通过不断变式具体地展示给学生，从而突破教学难点.例如在函数性质—奇偶性的学习时，为了真正理解奇偶函数的定义，可以对某一道习题作如下变式：

例1 已知函数 f（x）=loga（x+1），g（x）=loga（1－x）（a>o，且a≠1），求函数f（x）+g（x）定义域；判断函数f（x）+g（x）的奇偶性，并说明理由.（人教版第84页B组第4题）

变式1 已知f（x）=ax2+bx+3a+b是偶函数，定义域为a－1，2a.求实数a，b的值.

（A）x轴对称. （B）y轴对称.

（C）原点对称. （D）直线x－y=0对称.

上述三个变式训练尽管都是考察奇偶函数的相关知识点，但呈现方式比较隐蔽，即考点由明点变到了暗点，为学生理解奇偶函数概念内涵打下了基础.

3.2 加强条件变式，层层推进，直达“顶峰”

“问题是数学的心脏”“掌握数学意味着什么？那就是善于解题.”这是著名数学教育家G·波利亚的名言.数学问题千变万化，无穷无尽，要使学生身居考场而泰然处之，就必须有良好的解题应变能力，而应变能力在教学中是可以通过变式训练加以培养.那么学生的解题能力如何才能培养起来呢？教学中笔者对一道课本题做了如下一组变式训练尝试，效果很好.

例2 已知函数f（x）=x2－2x，g（x）=x2－2x（x∈2，4）．（人教A版第43页B组第1题）

（1）求f（x），g（x）的单调区间；（2） 求f（x），g（x）的最小值．

（2）试求函数y=－2x2－x+1在x∈－3，1上的最大值和最小值，并求出对应的x值.

变式1 函数y=ax在0，1上的最大值与最小值的和为3，则a的值为（ ）

变式2 若函数f（x）=logax（0<a<1）在区间a，2a上的最大值是最小值的3倍，则a的值为（ ）

变式3 已知函数f（x）=x2+4ax+2在区间（－∞，6）内单调递减，则a的取值范围是（ ）

（A）a≥3. （B）a≤3.

（C）a<－3. （D）a≤－3.

变式4 已知函数f（x）=x2－（a－1）x+5在区间12，1上为增函数，那么f（2）的取值范围是.

变式5 设函数f（x）=－x2+kx在2，4上是单调函数，求实数k的取值范围.

变式6 求二次函数f（x）=x2－2（2a－1）x+5a2－4a+2在区间0，1上的最小值g（a） 的表达式.

上述一系列的变式由易到难，通过层层推进的变式办法逐步让学生在解题中加强了对函数单调性的理解与应用的解题思路，完成了单调性与最值的相关知识重组与串联，对学生思维的缜密性提高与培养奠定了基础.

4 实证研究

国内外多项实验已经证明变式教学对学生的数学理解能力和数学成绩提高都有积极的影响，下面通过实验数据来检验变式教学对突破学生的数学思维障碍是否也有积极帮助.

4.1 实验对象

笔者选择所任教的两个相同层次班级的学生作为实验对象，包括有数学思维障碍的学生和没有数学思维障碍的学生.

4.2 实验组和对照组

将两个班级的学生随机分配到实验组和对照组.实验组采用变式教学方法，对照组采用传统教学方法.

4.3 实验内容

授课内容为函数奇偶性.在实验组中，采用变式教学法，包括多角度、多形式、多途径的教学方式，例如基于问题的学习，合作学习等等.在对照组中，使用传统的讲解、示范和练习等教学方法.

4.4 实验评估

通过考试和问卷等方式对实验效果进行评估.考试内容为函数奇偶性相关题目，考查学生对知识点的理解和应用能力.问卷包括两部分，一部分是关于学生自身数学思维障碍程度的评估，另一部分是关于他们对变式教学法的反馈意见.

4.5 数据分析

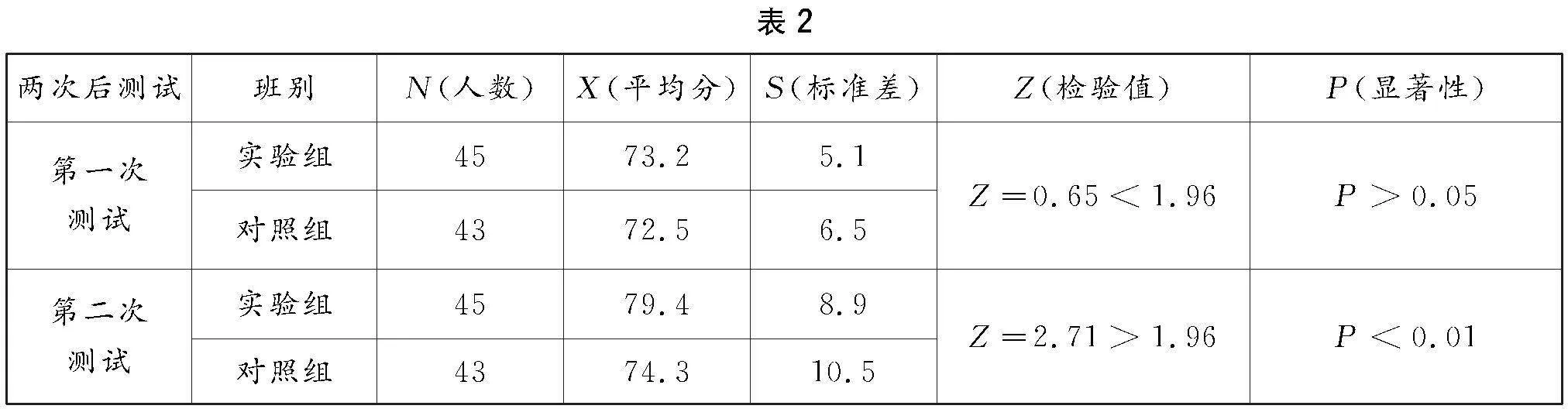
分别对实验组和对照组的考试成绩和问卷结果进行数据分析和比较，以评估变式教学法是否能够显著提升学生的数学思维能力和学习效果.具体统计如下：

表1数据说明，在采取不同的教学方式之前，两个班的均分相差0.6分，Z=0.37<1.96，则P>0.05，说明实验班与对照班没有显著性差异.表2数据说明，当第二次均分差距的增大到5.1分时，Z=2.71>1.96，P<0.01，可见两个班的差异是十分显著的.从而说明变式教学对突破学生数学思维障碍是有效果的.

5 结语

针对变式教学如何突破学生的两类数学思维障碍问题进行了深入分析和探讨.由于数学思维障碍是多种多样的，变式教学需要采用多种策略来应对不同的思维障碍问题，满足学生的个性化需求，促进其全面发展.

通过实证研究，证明了变式教学可以有效地突破学生的数学思维障碍，提高学生的学习成绩和兴趣度.在今后的数学教学中，应该进一步完善变式教学的理论框架和实施机制，并结合教育技术的发展，不断推进教学改革，有效地促进学生的数学思维发展，为培养具有创新精神和创造能力的高素质人才发挥数学作为基础学科的积极作用.

参考文献：

[1]孙发云.中职数学教学中数学思维能力的培养[J].教育艺术，2023，340（04）：46+48.

[2]吴光东.例谈变式教学在高中数学课堂中的应用[J].试题与研究，2023，1135（16）：34-36.

[3]陈萍萍.怎样开展对数函数变式教学[J].语数外学习（高中版中旬），2023，829（05）：48-49.

[4]孙立娜.如何突破高中数学思维障碍[J].人生十六七，2018（08）：115.

[5]楼春玲.学生数学思维障碍的原因剖析与突破策略[J].小学教学参考，2018（08）：71-72.