高中数学教学中圆锥曲线解题方法的研究

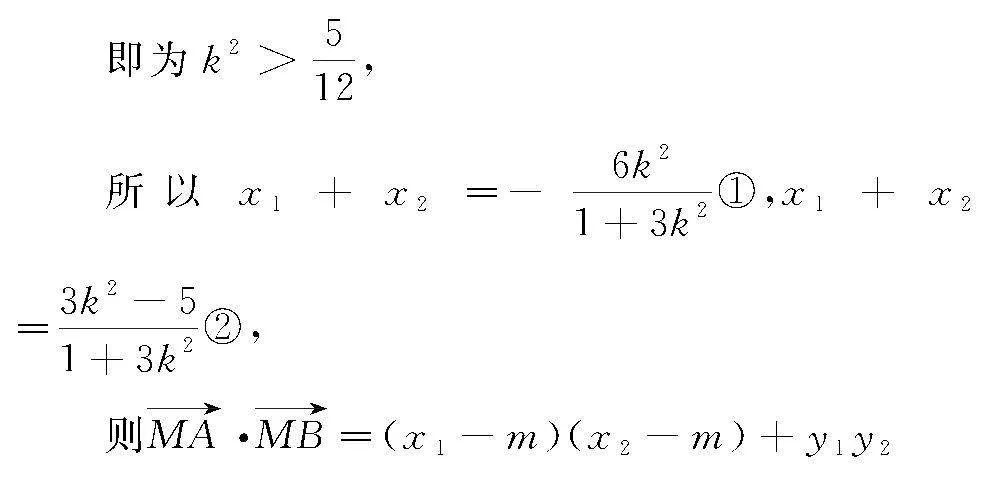
【摘要】解题训练属于高中数学教学中的常设环节，其中圆锥曲线题型灵活多变，难度较大，为提升学生的解题能力，教师需注重相关题型的介绍与对应解题方法的讲解，使其遇到相关习题时可以迅速破题，增强他们解答圆锥曲线类试题的自信心，为高考做准备.本文以高中数学教学中圆锥曲线解题方法为研究对象，同时分享一系列解题案例以供参考所用.

【关键词】高中数学教学；圆锥曲线；解题方法

圆锥曲线这一部分的知识较为特殊，以研究椭圆、双曲线和抛物线这三类圆锥曲线与方程为主，兼具几何与代数的双重特征，对学生的学习能力与解题能力均要求较高.在高中数学解题教学中，教师可围绕圆锥曲线题目设计专题训练，带领学生学习一些比较常用的解题方法，使其能用来有效解答圆锥曲线题目，由此提高他们解答圆锥曲线试题的水平.

1 运用方程解题方法，解答圆锥曲线位置问题

在高中数学解题教学中，经常会遇到判断直线和圆锥曲线的位置类试题，需要将直线和圆锥曲线的方程联立起来，转化成一元二次方程，运用方程解题方法，借助Δ进行判断.同时，还应注重灵活运用向量知识判断直线关系，如果题目中没有提示直线斜率是否存在，解题时还应注重展开分类讨论，不能遗漏任何一种满足题干要求的情形，确保对问题考虑的全面性[1].

分析 （1）可采用方程法，直接将椭圆和直线的方程联立起来进行化简，求出k的取值范围；（2）可结合方程及其他数学知识完成求解.

2 借助假设解题方法，解答圆锥曲线定值问题

针对高中数学圆锥曲线解题教学来说，求解定值类问题较常见.教师可以指引学生借助假设法进行解题，先结合已知条件把方程列出来，借助一元二次方程根和系数之间的关系，对要求解的定值表达式展开化简，让他们找到适当的切入点进行假设，使其通过假设列出相应的式子，如果表达式中带有参数，为保证其值为定值要将带参数的部分给消除[2].

分析 处理这类试题时，要先假设这样的点M存在，再根据题干中提供的条件进行分析和计算，如果不会出现冲突则说明该点的确存在，假如出现矛盾则说明该点不存在.

详解 假设在x轴上存在这样的一点M（m，0）满足题意，设A（x1，y1），B（x2，y2），

当直线AB的斜率存在，设为k，则对应的直线方程为y=k（x+1），将其同椭圆方程的联立起来消去y，由此得到（1+3k2）x2+6k2x+3k2－5=0，

则Δ=36k4－4（1+3k2）（3k2－5）>0，

=（x1－m）（x2－m）+k2（1+x1）（1+x2）

=（1+k2）x1x2+（k2－m）（x1+x2）+k2+m2，

将①②代入整理得到

当直线AB的斜率不存在时，其和x轴垂直，

3 结语

总而言之，圆锥曲线试题是高中数学考试中容易拉开分差的一类题型，教师应结合具体例题剖析不同题型的解题方法，带领学生进行针对性解题训练，要求他们做好解题的总结与反思工作，使其真正把握不同题型的解题规律和技巧，从而能够攻克这一难点题型.

参考文献：

[1]赵伟.高中数学圆锥曲线解题教学模式研究[J].数理天地（高中版），2023（19）：30-32.

[2]朱新保.关于一道圆锥曲线问题的解析探究与思考[J].数学教学通讯，2023（18）：86-88.

[3]马利民.高中数学教学中圆锥曲线的解题方法[J].数理天地（高中版），2023（11）：33-34.