关于三角函数问题构建示例的探究

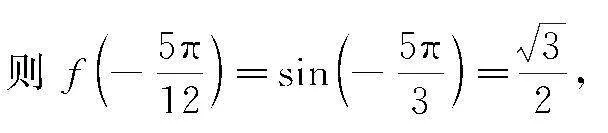
【摘要】三角函数是高中数学的知识重点，实际考查时常结合关联知识综合构建.问题解析建议开展命题分析，定位考点，再结合对应知识逐步剖析，必要时可绘制图象，结合函数的周期图象辅助分析.本文选取三角函数常见的三种构建情形，开展解题探究.

【关键词】三角函数；高中数学；解题技巧

三角函数是高中数学的重点内容，探究学习中需要掌握三角函数的单调性、对称性、周期等知识.问题考查构建形式多样，常与其他知识相融合，变换设问情形，综合考查学生的知识与能力.问题解析需要定位考点，结合知识要点逐步分析，下面结合考题举例探究.

1 三角函数与零点

考题1 （2023年新高考I卷第15题）已知函数fx=cosωx－1（ω>0）在区间0，2π有且仅有3个零点，则ω的取值范围是.

命题分析 本题目求三角函数的参数取值，核心条件为“在区间0，2π有且仅有3个零点”，显然考点为三角函数与零点.解题的关键是把握零点定义，转化条件信息，即令f（x）=0，得cosωx=1有3个根.后续可结合余弦函数的图象性质求解.

过程解析 因为0≤x≤2π，

所以0≤ωx≤2ωπ.

令f（x）=0，

得cosωx=1有3个根.

令t=ωx，

则cost=1有3个根，其中t∈［0，2ωπ］.

绘制如图1所示图象，由y=cost的图象性质可得4π≤2ωπ<6π，故2≤ω<3，

故答案为［2，3）.

解后评析 三角函数与零点问题较为常见，解题的关键有三点：一是理解零点的定义，掌握求解思路和转化方法；二是灵活绘制图象，结合图象直观分析；三是关注图象的周期变化，灵活变通调整变量.

2 三角函数与对称

命题分析 本题目要求解三角函数值，核心条件有两个：一是关于函数在区间上的单调性；二是关于函数的对称轴，显然为三角函数与单调性和对称性的综合问题.解题的关键是灵活使用三角函数的属性知识，结合题意合理转化.

故答案为（D）.

解后评析 上述将三角函数的图象、单调性、对称性交汇考查，构建了综合性较强的三角函数求值问题.探究解析的关键有两点：一是掌握基于y=Asin（ωx+φ），x∈R的图象求解析式的步骤；二是掌握三角函数关于直线的对称转化方法.

3 三角函数与平移

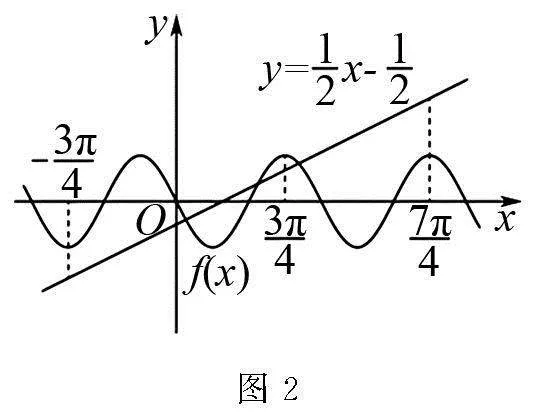
（A）1. （B）2. （C）3. （D）4.

解后评析 上述题目设定三角函数平移，求解平移后函数与直线的交点个数，综合性较强，该类问题建议结合图象分析.探究学习时注意知识总结：一是总结函数图形变换的方法步骤；二是掌握三角函数与直线相交的处理方法，注意特殊位置的大小比较.

4 结语

总之，三角函数问题是高考重点问题，探究学习中建议分三个阶段：阶段一，掌握基础知识，深刻理解其图象与性质属性；阶段二，开展拓展探究，构建知识关联，总结常见问题类型；阶段三，总结方法策略，结合实例强化训练.