动态的考查，静态的训练，动静转换以静制动

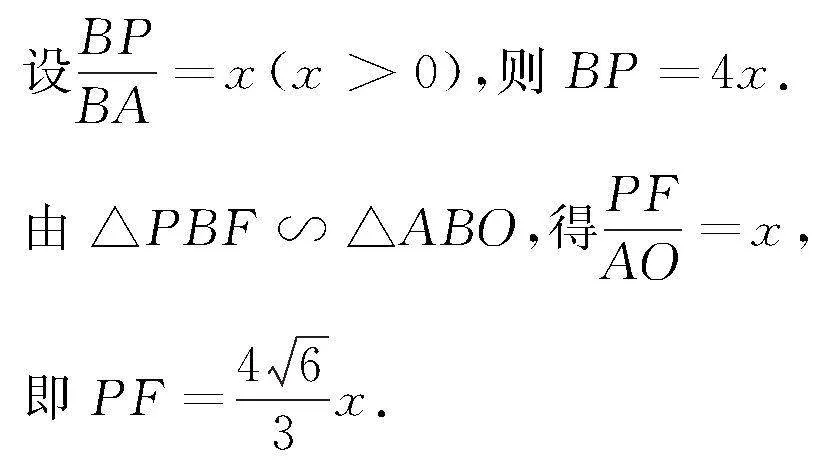
【摘要】对高考题进行静态设计，分组分任务完成，规范重点知识落实，把各自结果汇总，引领高一高二初学的学生观察归纳猜想寻觅规律；对高考题进行类题整合训练，多题归一，动态的最值问题，静态化思考，动静转换以静制动，提升认知境界，准确把握算法、算理、算律、规律，掌握解题教学的基本策略技巧．

【关键词】高中数学；法向量；解题技巧

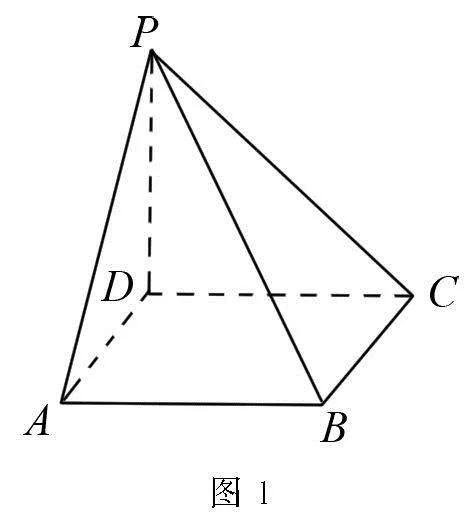
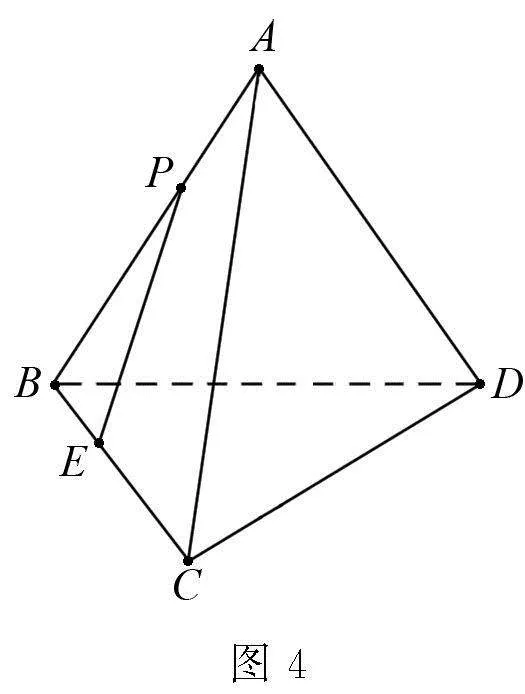
高考原题 如图1，四棱锥P—ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．

（1）证明：l⊥平面PDC；

（2）已知PD=AD=1，Q为棱l上的点，求PB与平面QCD所成角的正弦值的最大值．

试题评述 命题意图是考查空间向量在证明立体几何中的平行与垂直的位置关系，以及求线线角、线面角和面面角中的应用，属于中档题目．

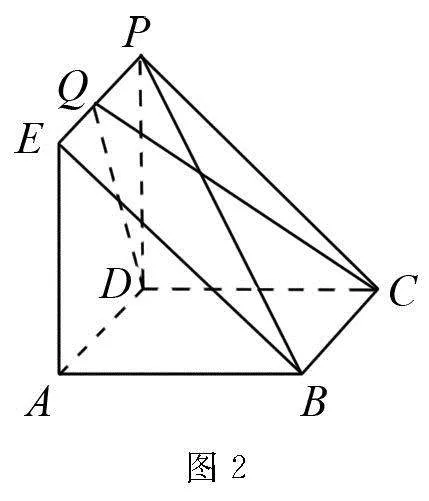
改造试题 如图2，三棱柱ABE-CDP的面ABCD为正方形，PD⊥面ABCD．已知PD=AD=1，Q为棱PE上的点，求PB与平面QCD所成角的正弦值的最大值．

改造意图 集中精力解决动态的线面角问题，优化解题教学结构，学会以静制动的解题策略，破解立体几何中的最值问题这个难点．对高考题进行微改造，一题多解，由薄到厚，拓展思维，使头脑丰富而厚重；对解法进行微创新，使知识横向、纵向联系，跨越章节时空范畴，发挥高考题目复习带动、辐射引领功能的最大化．最值问题是在点运动的过程中寻找出其边界值．着眼于线面角的最大值引领学生展开探究，一是对目标函数的构建方式进行微探究，构造方式有常规作图构造，补体转移构造和坐标构造以及普通基底构造等；二是对最值解法进行微探究，打通知识壁垒，架起沟通桥梁，从重视应试教育到更注重核心素养培育，形成融会贯通格局和浓厚研究氛围，多多挖掘试题内涵，对指导高三学生参加高考百利而无一害．

1 基于发挥试题复习功能，指导高三复习，一题多解，拓展思维

本文从一道高考题谈起，从①数学解题是注重本源的，②数学解题是强调变化的，③数学解题是讲究策略的这三个角

度各提供了3种共9种解法，已在《数理天地》高中版2021年第10期上发表，这里限于篇幅，就不再赘述．

二次思考 高考试题的命题意图主要是考查学生空间向量坐标运算的掌握情况，发挥坐标定位在解决空间立体几何最值问题中的优越性．本文命制了系列静态题组，把学生分成6个小组各自完成其中一题，然后汇总结果，再观察结果、归纳猜想、寻找规律，以期让学生在求解静态的线面角时彻底掌握基本解法，同时又能发现何时取得最值，领会知识形成过程，动态的最值学会静态化思考，实现以静制动．产生了如下教学策略，现展示出来供读者研究时参考．

2 基于引领突破教学难点，探究命题规律，多题一解，以静制动

开课时先复习空间向量的应用，线线角、面面角与线面角的向量表述公式形式高度统一．以下题目每组完成一题，预定时间10分钟，10分钟后分别找同学展示结果，把结果写成一行，观察大小变化是否有规律可寻．

变式6 如图2，三棱柱ABE-CDP的面

3 基于借助规律巩固成果，形成核心素养，类比探究，螺旋提升

数学核心素养是育人价值的集中体现，包括数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析．具体到这类试题，命题最终考查的是什么？是较高的逻辑推理和数学运算能力，也是选拔数学优等生的必然追求．以下设计的系列跟踪训练题目，多题归一，思考其为何落点如此一致.理清问题实质．

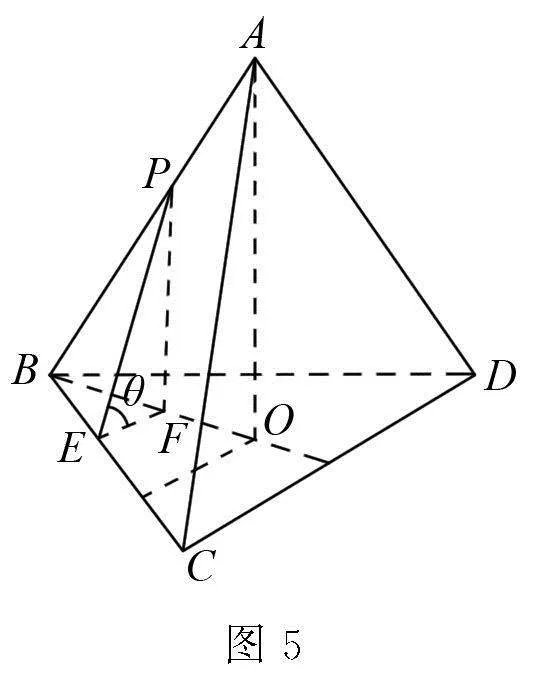
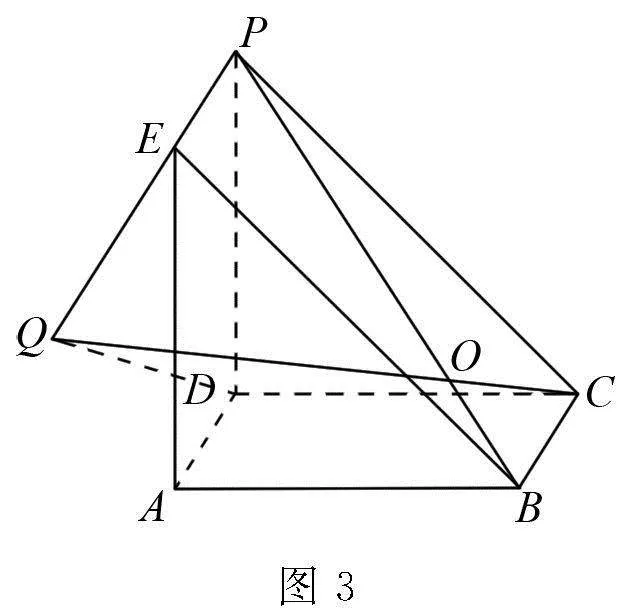
解析 作AO⊥平面BCD于点O，则点O是△BCD的中心，如图5.

则∠PEF为所求的EP与平面BCD所成的角θ．

在△PBE中，由余弦定理得

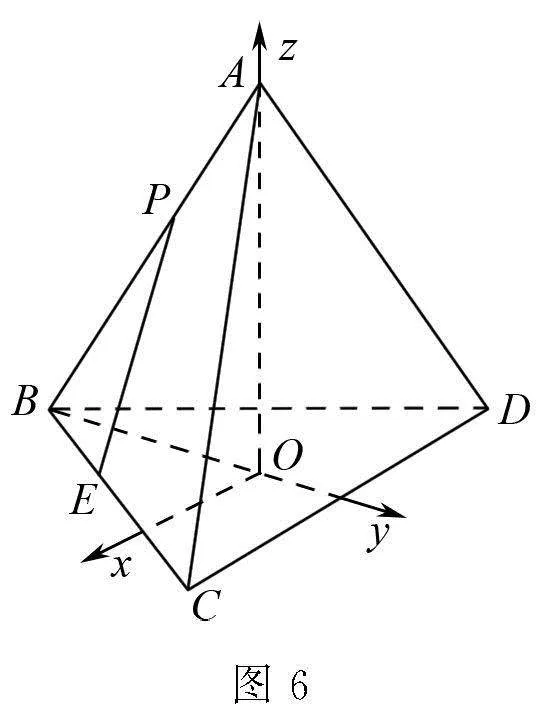
解析 建立如图6所示的空间直角坐标系，设正四面体的棱长为3，

跟踪训练变式题 如图7，在正方体ABCD-A1B1C1 D1中，点O为线段BD的中点，点P在线段CC1上．若直线OP与平面A1BD所成的角为θ，求sinθ的取值范围．

4 结语

数学解题教学是数学教师以学生的解题学情为起点，高三学生和高一高二学生解题经验、知识储备、综合素养等有着明显的不同，需要教师以自身的解题经历、经验和研究为基础区别对待．通过系列化题组设计，引领学生探究，促进深度思考，优化学生的思维品质．

【山东省教育教学研究课题“大单元视域下普通高中数学任务链进阶驱动教学的实践研究”2023JXY343的中期成果】

参考文献：

[1]章建跃.理解学生 理解数学 理解教学 理解技术[J].中国数学教育（高中版），2010（12）：1-5．

[2]杨华文.从一道高考题谈起[J].数理天地（高中版），2021（10）：22-25．