高中数学函数解题中化归思想的合理运用

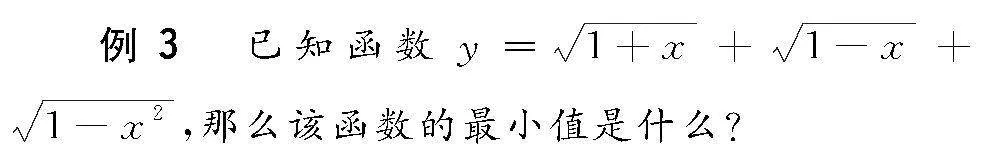
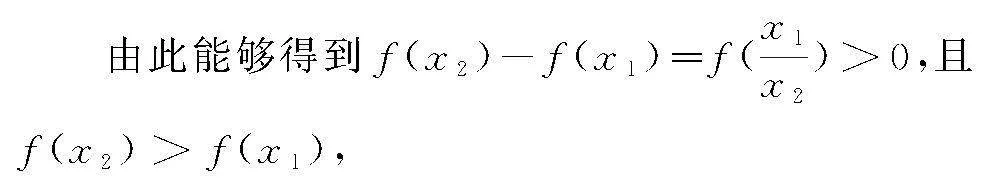
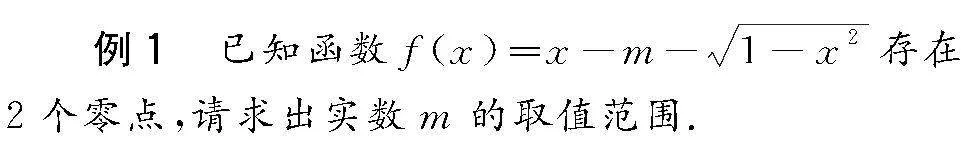
【摘要】函数作为高中数学课程体系中的一项重要内容，涉及的知识点繁多，相应的习题种类也较多.在解题训练中，仅仅依靠常规方法难度较大，甚至会走不少弯路，影响解题训练的正常推进.面对这一不利局面，教师在具体的函数解题教学中，可以指导学生合理运用化归思想，让他们通过化归找到简便的解题方法，使其顺畅完成解题.本文以高中数学函数解题中如何运用化归思想为主要研究对象，并罗列出部分解题案例.

【关键词】高中数学；函数解题；化归思想

化归思想其实是转化与归结的统称.将一个问题由复杂化简单、由繁化简、由难化易的过程就是化归.化归思想既是一种重要的解题方法，还是一种比较常用的解题思维与策略，可以用来解答多个方面的试题.针对高中数学函数解题训练来说，教师应当帮助学生学会合理运用化归思想，把函数问题进行转化和化归，使其在化归思想助力下灵活采用函数的性质与图象等进行解题，掌握更为科学的解题流程和方法，最终让他们能够高效率地处理函数试题.

1 合理运用数形化归，形象解答函数试题

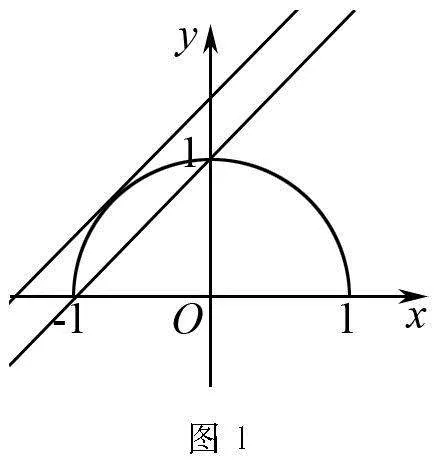
数学知识主要包含代数和几何两大类，与之分别对应的便是“数”和“形”.函数知识具有典型的数形结合特征，在解题训练中，十分适合化归思想的运用.通过数形转化的方式来应用化归思想，这在处理函数类试题中相当常用，且比较有效.在高中数学函数类题目中，尽管部分数量之间的关系有着抽象特征，但是可通过几何图形形式来呈现，教师可引领学生合理运用数形化归，使其把抽象的函数试题以直观、形象的形式呈现而出，促使他们迅速确定解题的切入点[1].

分析 从题目中给出的函数解析式来看，尽管式子比较复杂，但是可以从存在2个零点这一隐含条件着手，展开数和形之间的化归，通过观察发现可

2 一般向特殊化归，降低试题复杂程度

一般向特殊化归也是化归思想的一个重要形式，在高中数学解题中有着广泛的应用范围，其中在处理函数方面的试题时，当采用一般方式难以解决时，教师就要想到一般向特殊的化归，引领学生尝试运用特殊法来进行求解，往往能够起到由繁至简、从难到易的效果.故教师在平常的函数解题教学中，需有意引领学生运用一般到特殊的化归思想，降低题目的复杂程度与难度，助推他们顺畅地完成解题[2].

例2 已知函数f（x）且（x∈R，x>0），在该定义域内的任意实数x，y均可满足f（xy）=f（x）+f（y），而且当x>1时，f（x）>0，证明方程f（x）=0只有1个实数根.

分析 这道函数试题既复杂又抽象，还涉及方程，不过可以借助化归思想的优势把一般性问题当作特殊化问题来对待，从而对题意进行更好的分析与判断，最终找到正确的解题思路与方法，在解题中少走弯路，简洁地完成解题.

详解 在定义域内任意取0<x1<x2，

又因为f（xy）=f（x）+f（y），

所以f（x）=f（xy）－f（y），

那么可以判断出函数f（x）在定义域内是一个增函数，

然后令x=y=1，

则f（1）=2f（1），即为f（1）=0，

故1是方程f（x）=0的1个实数根，

假如还有另外1个实数根x0，且x0>0，使得f（x0）=0，

因为函数f（x）在定义域内是一个增函数，

所以必有x0=1，

所以说f（x）=0只存在1个实根，即为x=1.

3 合理运用正反化归，开阔学生解题思维

在高中数学函数解题训练中，部分函数题目有着一定的特殊性，通过证明思维与常规方法虽然也可以完成解题，不过显得比较麻烦，学生在做题时经常会产生失误现象，导致正确率受到影响.其实，高中数学教师在日常函数试题解题训练中，可引导学生合理运用正反化归思想，从反面或者其他面分析和处理试题，使其解题思维变得开阔起来，拓展解题空间，让函数问题变得更为简单化，难题自然迎刃而解，从而提高解题效率[3].

分析 这一函数试题的题干较长，是三个根式

4 结语

总而言之，在高中数学函数解题教学实践中，教师应把握好函数理论知识的特征及常见题目类型的特点，通过平时教学帮助学生奠定坚实的理论基础，在做题环节引领他们合理运用化归思想进行解题，使其根据题目的实际情况与解题需求灵活数展开转化与归结，确定恰当的解题方案与思路，让他们顺利求得题目的结果，继而不断提升数学解题水平.

参考文献：

[1]于佳淼.高中数学常见的思想方法在函数解题中的应用[J].教育界，2021（50）：5-7.

[2]高登.探析化归思想在高中数学函数学习中的运用[J].数理化学习（教研版），2021（10）：5-6.

[3]谢光琦.浅谈高中数学函数教学中化归思想的应用[J].高考，2020（15）：52.