三角形场景创设，诱导公式妙应用

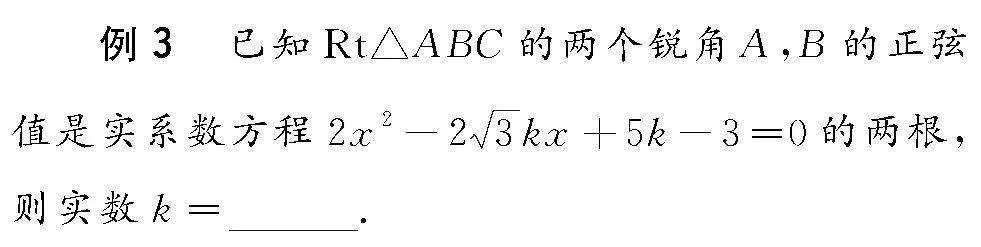
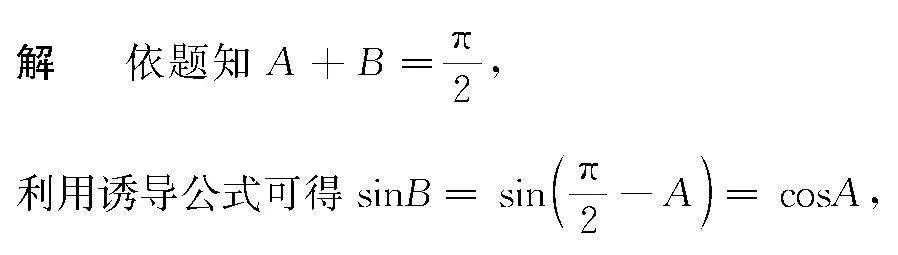
【摘要】诱导公式是三角函数中的一类基本公式，对于三角关系式的化简、求值以及证明等都有特殊的应用．而以三角形为场景的三角函数问题，对于诱导公式的应用更加灵活多变，巧妙融入三角形的内角和公式以及相关的性质，在多种情况下都有重要作用，可引领并指导数学教学与应用．

【关键词】高中数学；三角函数；诱导公式

诱导公式巧妙揭示了终边具有某些对称关系的两个角的三角函数之间的关系，可以有效地将终边对称的图形关系直观地“翻译”成三角函数之间的代数关系，对于三角函数中的化简、求值、证明等相关问题的应用有实效．同时，诱导公式也巧妙地将函数与方程、不等式、几何问题等联系起来，成为三角函数知识考查中的一个基本点．利用诱导公式处理与解决一些与三角形相关的问题，备受各方关注．

1 命题的判断

在三角形中，借助三角形的基本性质，结合诱导公式的应用，可以用来判断一些涉及三角函数式的变换与应用问题．此类场景中，往往基于三角形背景来判断一些三角关系式是否成立．

例1 （多选题）已知A，B，C为△ABC的三个内角，下列结论正确的是（ ）

分析 根据题设条件，利用三角形的内角和定理构建关系式A+B+C=π，代入各选项中，利用对应的诱导公式加以分析与应用，进而对比各选项中结论的真假．

解 在△ABC中，由三角形的内角和定理有A+B+C=π，

而cos（A+B）=cos（π－C）=－cosC，选项（D）错误；

故选择答案：（A）（B）（C）．

点评 在具体判断三角函数关系式是否成立时，基于三角形的内角和定理，合理代换处理，充分利用诱导公式加以变形与转化，有效减少角的个数，方便三角关系式的变形或化简，为三角关系式是否成立的判断提供条件．

2 等式的证明

在三角形中，有关三角形中相关角的三角函数式的证明与应用问题，离不开三角形的基本性质与诱导公式的应用．此类场景中，往往基于三角形背景证明一些内角之间的代数关系或内角的三角函数值之间的关系式成立等．

例2 已知A，B，C为△ABC的三个内角，且满足sinC=sinB（1+2cosA），试证明：A=2B．

分析 根据题设条件，利用三角形的内角和定理，并结合诱导公式的应用对题设三角关系式进行变形，结合三角恒等变换公式的应用，得到sinB=sin（A－B），进而分两种情况加以分类讨论．

证明 由三角形的内角和定理有A+B+C=π，

则有sinC=sinπ－（A+B）=sin（A+B），

依题可得sinC=sinB（1+2cosA）=sin（A+B），

所以sinB+2sinBcosA=sinAcosB+cosAsinB，

整理有sinB=sinAcosB－cosAsinB，

可得sinB=sin（A－B），

则有B=A－B或B+（A－B）=π，

可得A=2B或A=π（舍去），

所以A=2B成立．

3 参数的求值

在三角形中，涉及与之相关的含参函数与方程、不等式等问题，经常借助三角形的基本性质、同角三角函数基本关系式以及诱导公式等的综合应用来分析求解．此类场景中，往往基于三角形背景设置方程的根与应用等．

分析 根据题设条件，利用直角三角形的结构特征构建两锐角的关系式，并结合诱导公式建立三角关系式，同时利用方程的根的条件以及韦达定理构建关系式，利用平方和的关系转化为涉及含参数的二次方程，利用方程的求解以及分类讨论验证确定参数的值．

则有sin2A+sin2B=sin2A+cos2A=1，

所以（sinA+sinB）2=sin2A+sin2B+2sinAsinB=1+5k－3=3k2，

整理有3k2－5k+2=0，

点评 在解决涉及三角形中的函数与方程问题时，要综合考虑三角形的基本性质，以及函数与方程的基本知识．如该问题中二次方程有根的判别式条件，以及对应的三角函数值的取值在范围0，1内，等等，都是题目的隐含条件，在实际解题过程中要加以充分考虑与分析应用．

4 结语

利用诱导公式解决三角形场景下的综合问题，关键是合理把握三角形的基本性质，正确应用诱导公式的相应规律，同时要注意三角形中各内角均为（0，π）上的角，以及三角形的三个内角和为π这些条件的限制，将其综合起来加以分析与研究．