浅谈有关恒成立问题的解题策略与技巧

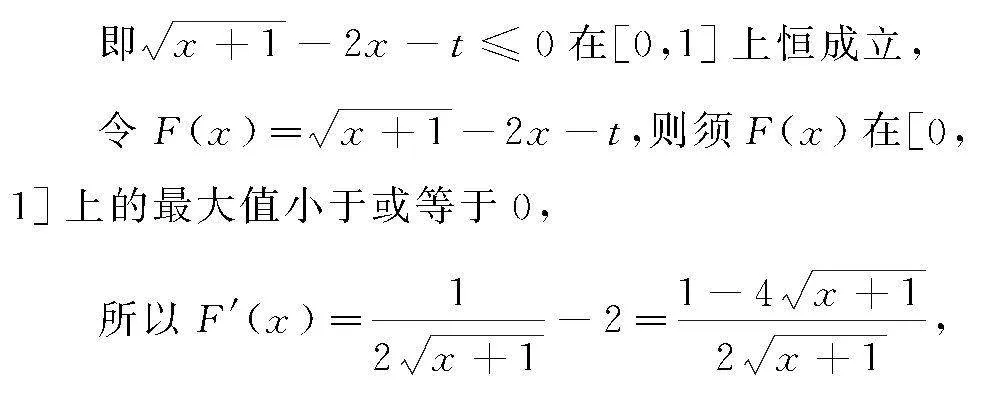
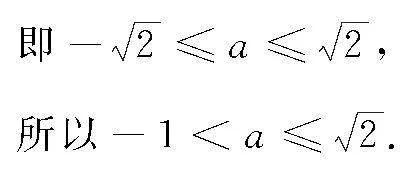
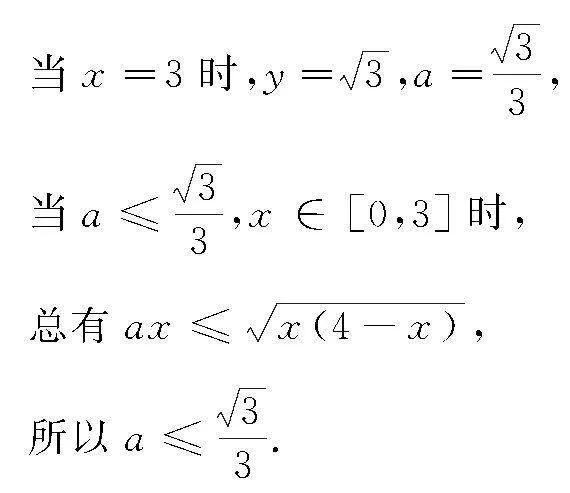
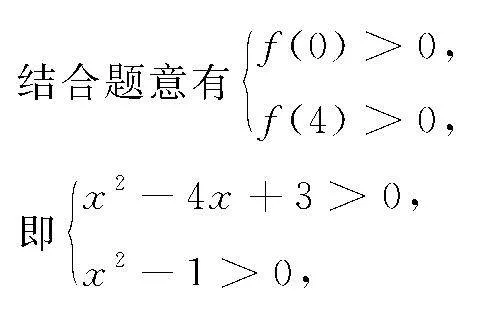
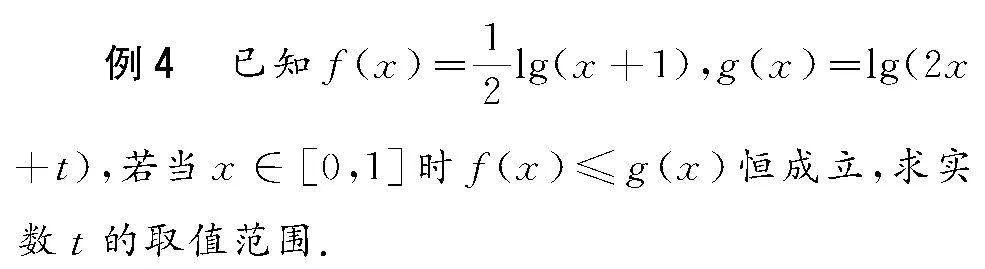
【摘要】本文通过探讨数学问题中恒成立的情况，总结解题的常见策略和解题技巧，并通过具体案例展示这些技巧在实际问题解决中的应用，以期为读者提供解决恒成立问题的有效途径.

【关键词】高中数学;恒成立问题;解题

在解决恒成立问题的过程中往往需要我们发挥创造性思维，巧妙地运用数学知识和技巧证明或判断某个恒等式或不等式是否成立.希望通过本文的讨论，读者能够更好地掌握解决恒成立问题的方法，提高解题的效率和准确性.

1 转化为二次函数，利用分类讨论思想解题

例1 已知函数f（x）=x2－2ax+4在区间［－1，2］上都不小于2，求a的值.

解 由函数f（x）=x2－2ax+4的对称轴为x=a，

所以必须考查a与－1，2的大小，显然要分三种情况进行讨论.

①当a≥2时，f（x）在［－1，2］上是减函数，

此时，f（x）min=f（2）=4－4a+4≥2，

③当－1<a<2时，

f（x）min=f（a）=a2－2a2+4≥2，

2 确定主元，构造函数，利用单调性解题

例2 对于满足0≤a≤4的所有实数a求使不等式x2+ax>4x+a－3都成立的x的取值范围.

解 不等式变形为x2+a（x－1）－4x+3>0，

设f（x）=x2+a（x－1）－4x+3，

则其是关于a的一个一次函数，是单调函数，

解得x<－1或x>3.

3 利用不等式性质解题

例3 若关于x的不等式x－2+x+3≥a恒成立，试求a的范围.

解 由题意知，只须

a≤（x－2+x+3）min，

由x－2+x+3≥|x－2－（x+3）|=5，

所以a≤5.

4 构造新函数，利用导数求最值

解 f（x）≤g（x）在［0，1］上恒成立，

又x∈［0，1］，

所以F′（x）<0，

即F（x）在［0，1］上单调递减，

所以F（x）max=F（0），

即F（x）≤F（0）=1－t≤0，得t≥1.

（说明：若将恒成立改成有解，即f（x）≤g（x）在［0，1］上有解，则应F（x）min≤0.）

5 分离参变量，变换成函数问题

例5 已知二次函数f（x）=ax2+x+1对x∈0，2恒有f（x）>0，求a的取值范围.

解 对x∈0，2，恒有f（x）>0，

即ax2+x+1>0变形为ax2>－（x+1），

当x=0时，对任意的a都满足f（x）>0，因此只需考虑x≠0的情况，

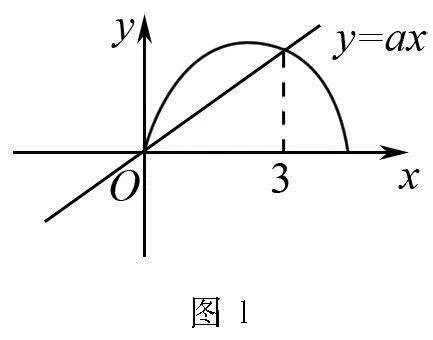
6 利用数形结合解题

7 结语

通过本文的探讨，我们对有关恒成立问题的解题策略与技巧有了更深入的了解.恒成立问题在数学中具有重要的意义，解决这类问题需要我们熟练掌握代入特定值、化简、利用数形结合等解题策略和技巧.同时，也注重在解题过程中培养创造性思维和逻辑推理能力，灵活运用各种数学知识来解决问题，激发学生对数学问题的探索和思考，为数学学习和解题能力的提升提供有益的参考.

参考文献：

[1]郭维.恒成立问题的三种常用解法[J].高中数学教与学，2020（02）：46-47.

[2]郑建.高中数学不等式恒成立问题解题思路探究[J].考试周刊，2020（49）：71-72.

[3]李树栋.例析解答不等式恒成立问题的途径[J].语数外学习（高中版下旬），2020（08）：52+69.