高中数学解题中函数思想的运用策略

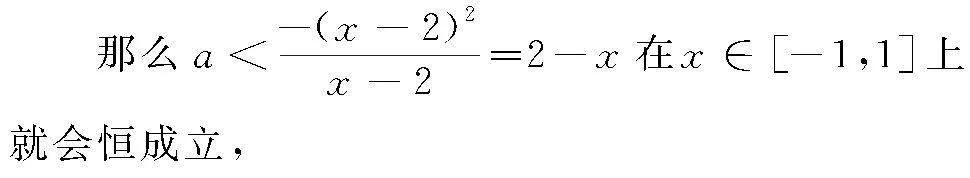
【摘要】在高中数学教学中函数模块占据着重要的地位，其能够基本贯穿整个数学知识体系.此外，函数思想也是一种十分常见的数学思想，学生能够运用该思想快速解答数学问题.因此，教师在开展解题教学时，需要为学生详细讲解函数思想的内涵，并通过典型例题培养学生掌握相应的解题技能.

【关键词】高中数学；解题教学；函数思想

函数思想是一种高中学生解答数学问题的常用解题策略.要想熟练运用函数思想解答数学题目，高中学生就需要了解函数思想的内涵[1].实际上，学生在深度学习中能够发现，函数思想主要是运用了变量与定量间存在的关系，运用一个事物随着另一个事物的改变而产生变化的规律.因此，高中数学教师在开展解题教学时，就需要引导学生将已知条件转变为数学语言，并据此建立相应的函数关系，进而找出正确答案.

1 利用函数思想解答集合类的数学问题

集合模块的知识是整个高中数学体系中较为基础的内容，其是学生在高中阶段最初学习的知识要点[2].当使用函数思想来解析集合类数学问题时，授课教师首先需要引导学生探究函数与集合间可能存在的关系.实际上，我们能够将函数转变为2个集合的映射，即包含函数值与自变量两个集合.

解析 阅读题干信息可以发现，其向我们表明了2个集合存在的关联，集合中还包含了不等式的内容，如果学生采用常规思维进行思考，则解题过程十分复杂、繁琐，很容易在解题中出现错误.因此，授课教师可以引导学生借助函数思想来分析函数值与自变量之间的关系，进而明晰解题流程.

以下为具体解题过程：

把集合A简化处理后能够列出：

A=xx>1且x<3.

假设f（x）=x2－2x+m，

g（x）=x2－2nx+5，

那么B1=xx2－2x+m≤0，

B2=xx2－2nx+5≤0，

B=B1∩B2，

因此能够推出f（1）≤0，f（3）≤0，

且g（1）≤0，g（3）≤0.

将对应数值代入题干中的不同式子后就可发现m与n的取值范围，从而大大降低解题难度.

2 利用函数思想解答不等式类的数学问题

函数模块知识与不等式模块知识看似不相关，实+EqFE6bDYPqEgcG7ThSfKg==际上在高中数学解题过程中却存在密切联系，数学教材中还有“不等式与二次函数”的教学内容，这也是为了帮助学生利用函数思想解决不等式问题作铺垫[3-4].学生在探究中需要运用不等式的性质而推断函数单调性的特征，进而快速解答恒成立与最值问题.

例2 假设对任意x∈［－1，1］，均保证f（x）=x2+（a－4）x+4－2a数值大于0恒成立，那么请大家推断a的取值范围.

解析 在拿到这一题目后很多学生感到难度较大，不好下手，教师就可鼓励学生直接借助函数思想来探究，并将原本的题干信息转变为：在一闭区间内存在某一个含参数的二次函数始终大于0的问题，整合后得出a的取值范围，即：a<1.

以下为具体解题过程：

对于任意x∈［－1，1］，f（x）=x2+（a－4）x+4－2a上的数值都会比0大，

因此x2+（a－4）x+4－2a>0，

得出a（x－2）>－x2+4x－4，

由于x∈［－1，1］，

所以a<（2－x）min，

那么当x=1时，（2－x）min=1，由此得出a<1.

在拿到题目后学生需要有效借助函数思想来探究，整个解题环节中学生不需要分析Δ<0的情况，这不仅能够保障所有情况不被遗漏，更能够提高学生的解题正确率，让学生快速得出正确答案.

3 利用函数思想解答数列类的数学问题

数列模块的知识属于高中数学体系中的一大核心内容，也是高考中的必考知识点.因此，学生不mkOrasai8/Xz1ImHTnUg8w==仅需要掌握数列的概念和内涵，还需要了解如何运用等差、等比数列的相关知识解答数学问题[5].实际上，数列能够归为函数的延伸产物，如果一个函数的定义域是正整数集，那么就能够将这一函数看作数列.在数列习题训练时，尤其针对求解最值的数列问题，授课教师可以引导学生运用函数思想来解答，从而减少解题流程，快速得出正确答案.

解析 若高中学生纯粹根据数列的相关知识进行求解，虽然能够计算出正确答案，但解题过程较为繁琐复杂，更容易在求解中出现错误，最终影响正确率.因此，数学教师可以鼓励学生使用函数思想进行探究，试图从题干信息中找出变量，并明晰量与量之间的函数关系，进而得出答案.

以下为具体解题过程：

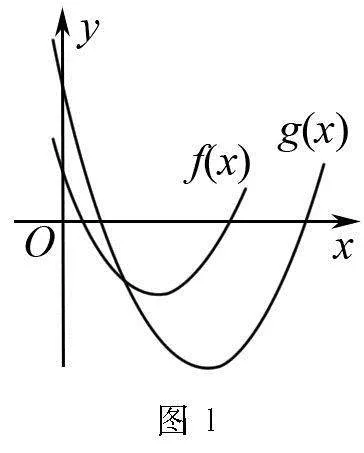
阅读题干后能够得出f（x）=3x2+1，g（x）=5x，

由此推断bn=6a2n－5an+1，n∈N*，

将相关数值代入后可以得出：

4 结语

综上所述，在高中数学教学中，随着课堂知识深度与难度的逐步提升，导致数学问题的解题难度也逐渐攀升，授课教师需要传授学生便捷、有效的解题技能，从而帮助学生快速找出问题的答案.利用函数思想能够将很多常见的数学问题转变为函数问题，让学生突破传统解题模式的障碍，快速找出关键点，最终将复杂的题目直观化、简单化.

参考文献：

[1]谭雪妗.函数与方程思想破解高中数学教学难点探析[J].数理化解题研究，2023（18）：2-4.

[2]朱坤密.基于函数思想的高中数学解题探究[J].数学学习与研究，2023（18）：108-110.

[3]马艳波.新课程背景下高中数学变式题设计方法探析——以“数形结合思想在函数问题中的应用”一课教学为例[J].延边教育学院学报，2022，36（03）：143-145.

[4]杜维达.数学素养视域下利用函数与方程思想破解高中数学教学难点的案例研究[J].读与写：（下旬），2022（07）：10-12.

[5]张天涛.运用函数思想解决高中数学问题的研究[J].中华活页文选（高中版），2022（05）：112-114.