双曲线焦半径及焦点弦公式的推导及其应用

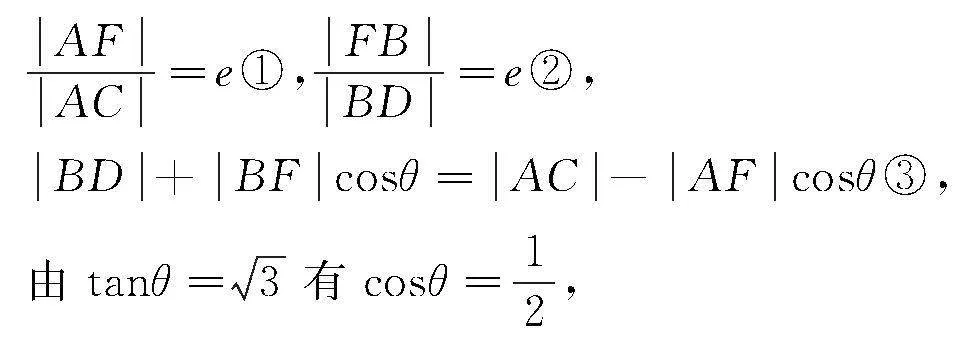
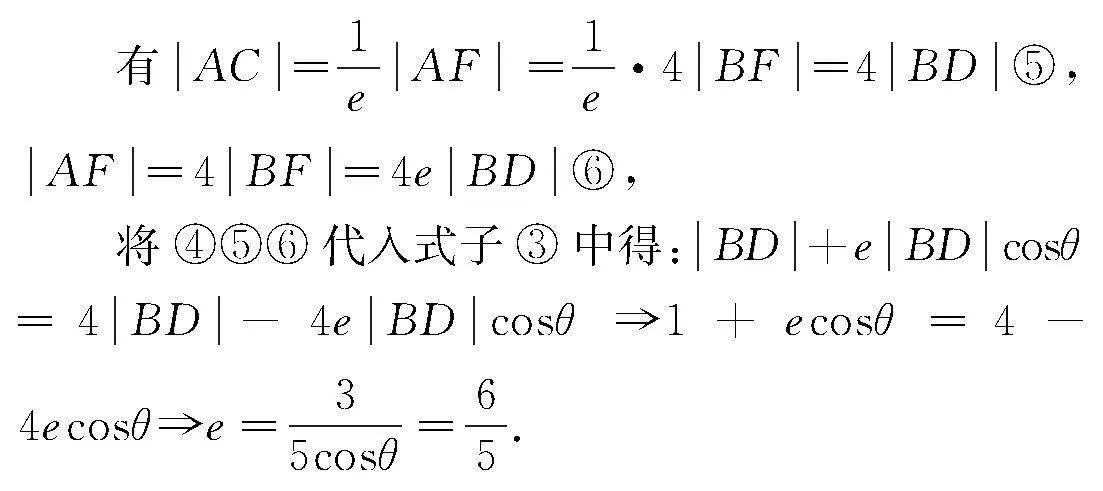
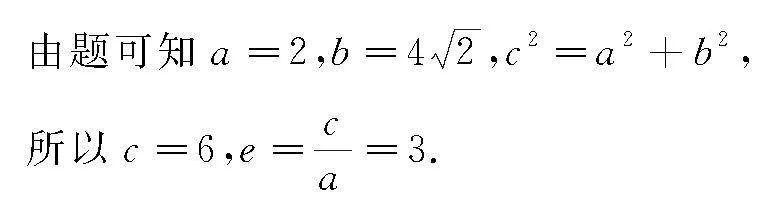
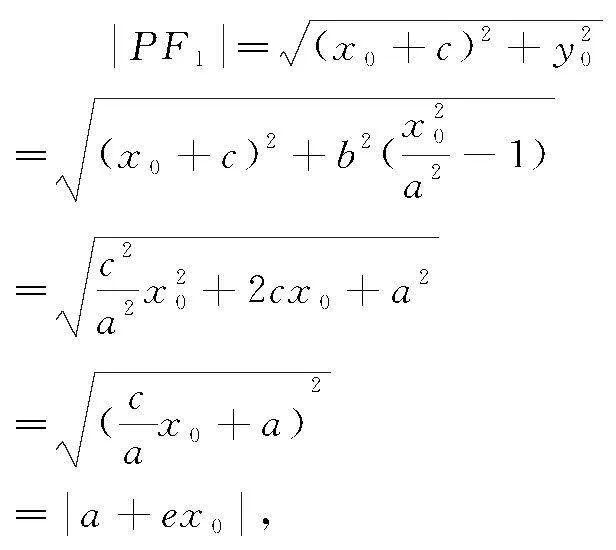
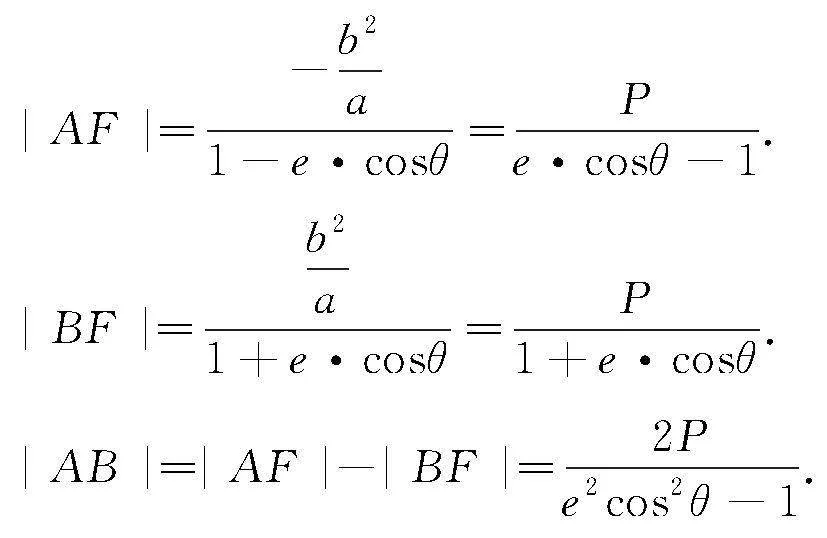
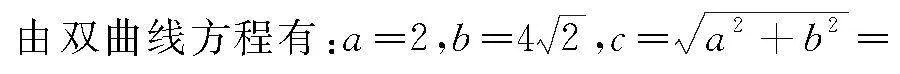
【摘要】本文主要介绍双曲线焦半径及焦点弦公式的推导，分析其如何在题目中巧妙运用.

【关键词】双曲线;高中数学;解题技巧

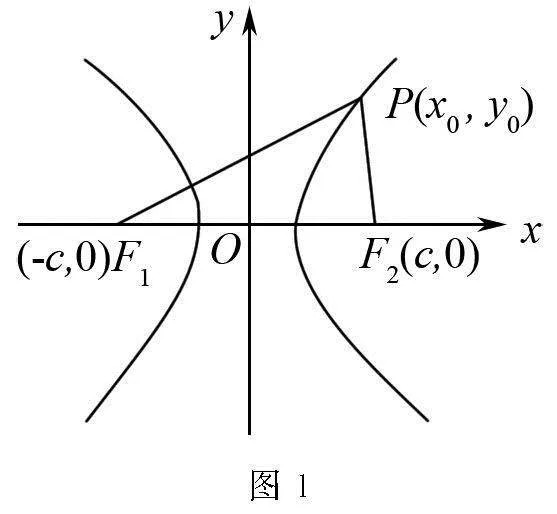
1 双曲线坐标式焦半径公式推导及应用

由两点间距离公式可得：

同理得：PF2=a－ex0，

当P在右支上时，x0≥a，

PF1=a+ex0，PF2=－（a－ex0），

当P在左支上时，x0≤－a，

PF1=－（a+ex0），PF2=a－ex0.

解法1 普通解法

解法2 焦半径公式

由焦半径公式得－（a－ex0）=2x0，

所以x0=2.

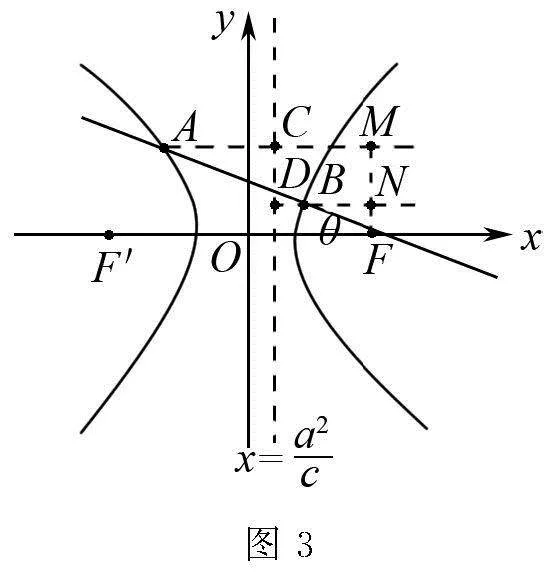
2 双曲线角度式焦点弦公式推导及应用

2.1 交于双曲线同支的焦点弦

2.2 交于双曲线异支的焦点弦

如图3所示，证法与2.1一致，因此，角度式的焦半径和焦点弦公式可以总结如下：

解法1 普通解法

设所求离心率为e，则由图2可知：

由②，有BF=eBD④，

由①④及已知条件，

解法2 焦点弦公式

参考文献：

[1]吴家华.椭圆“三个定义”的等价性与隐蔽性[J].数理化学习（高中版），2023（10）：28-33.

[2]卢艳华，尹伟云.圆锥曲线中焦半径系列公式的运用[J].中学数学杂志，2022（09）：34-39.

[3]中华人民共和国教育部.普通高中数学课程标准（2017年版）[S].北京：人民教育出版社，2018.