高中数学有关抽象函数的对称性和周期性的探究

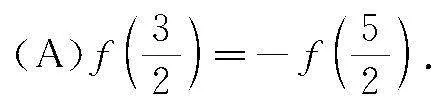
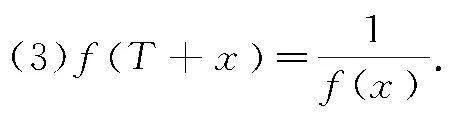
【摘要】抽象函数的对称性和周期性在高考数学中具有重要的地位，掌握这些概念对于解决各种数学问题和应对高考数学考试至关重要.本文旨在探究抽象函数的周期性和对称性在数学中的应用，探讨如何更好地理解和应用抽象函数的对称性和周期性，分析其特点和规律，最后巧妙地利用这些性质来解决相关的数学问题.

【关键词】抽象函数；高中数学；解题技巧

1 引言

抽象函数是高中数学中一个重要的概念，对称性和周期性是其重要的性质，它们反映了函数的内在结构和变化规律，对于研究函数的图象、性质和应用都有着重要的意义.近两年高考真题中出现的抽象函数和导数的交汇题型增加了题目的思维难度，对学生的创新思维提出了更高的要求.面对这样的挑战，学生需要在平时做题时注重对数学知识的深入理解，在掌握基础知识的同时灵活运用知识，从复杂的情境中抽象出数学模型.

2 抽象函数的对称性和周期性实例探究

例1 已知定义在R上的偶函数fx满足f1－x=－f1+x，下列说法正确的是（ ）

（B）函数fx的一个周期为2.

（C）f2023=0.

（D）函数fx的图象关于直线x=1对称.

f2023=f3=f－1=f1=0，选项（C）正确.

规律总结：若函数满足下面三个等式之一，

（1）fa+x=－fa－x；

（2）f2a－x=－fx；

（3）f2a+x=－f－x.

则y=fx关于点a，0中心对称.

例2 已知y=fx是定义域为R的奇函数，若y=f2x+1的最小正周期为1，则下列说法中正确的个数是（ ）

（A）1个. （B）2个. （C）3个. （D）4个.

解析 y=f2x+1的最小正周期为1，所以f2x+1+1=f2x+1；即f2x+3=f2x+1，f（x）的周期为2；

因为fx+2=f（x）=－f（－x），所以f（x）的一个对称中心为（1，0），③正确；

规律总结：若函数满足下面三个等式之一，

（1）fa+x=fa+x+T；

（2）fT+x=－fx；

则y=fx为周期函数.

例3 已知函数y=f2x+1的图象关于直线x=1对称，函数y=fx+1的图象关于点1，0对称，则下列说法正确的是（ ）

（A）f1=0.

（B）fx是奇函数.

（C）f1－x=f1+x.

（D）fx的周期为4.

解析 由函数y=f2x+1的图象关于直线x=1对称，得f2x+2+1=f2－2x+1，即f3+2x=f3－2x，将2x换为x可得fx+3=f3－x，所以fx的图象关于直线x=3对称.

由函数y=fx+1的图象关于点1，0对称，得函数y=fx的图象关于点2，0对称，即fx+f4－x=0.所以fx的对称轴x=3关于2，0的对称直线x=1也是fx的对称轴，（C）正确；所以fx的对称中心2，0关于x=1的对称点0，0也是fx的对称点，（B）正确；又fx=－f4－x=fx－4，所以fx+4=fx，fx的周期为4，（D）正确.

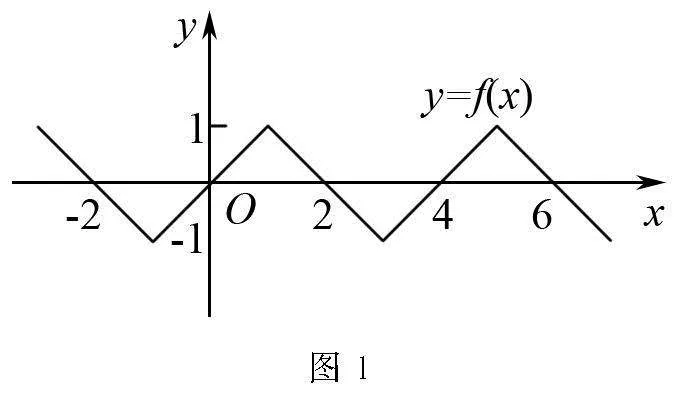
根据以上性质，不妨作出满足函数fx性质的一种图象情况，如图1.

由图可知，此时f1=0不成立，（A）错误.故选：（B）（C）（D）．

若函数f（x）的满足题设条件，则函数f（x）+C（C为常数）也满足题设条件，无法确定f（x）的函数值，故（A）错误.故选：（B）（C）.

方法2 特殊值，构造函数法

3 结语

本文的研究旨在帮助学生更好地理解和掌握抽象函数的对称性和周期性，提高学生的数学素养和解题能力，还可以为其他数学研究提供有益的参考和借鉴.同时，本文的研究也有助于推动数学教育的改革和发展，提高数学教育的质量和水平.

参考文献：

[1]夏朴.借助抽象函数模型，解决函数性质问题[J].中学生数理化（高考数学），2023（09）：18-20.

[2]袁安.变易图式在抽象函数性质教学上的应用研究[J].中学数学研究（华南师范大学版），2020（22）：34-37.

[3]孙志鹏.抽象函数及其导函数的性质探究及应用[J].高中数理化，2023（13）：43-44.