巧构齐次式，妙解几类题

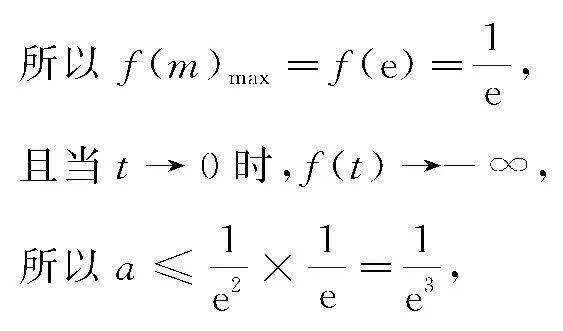
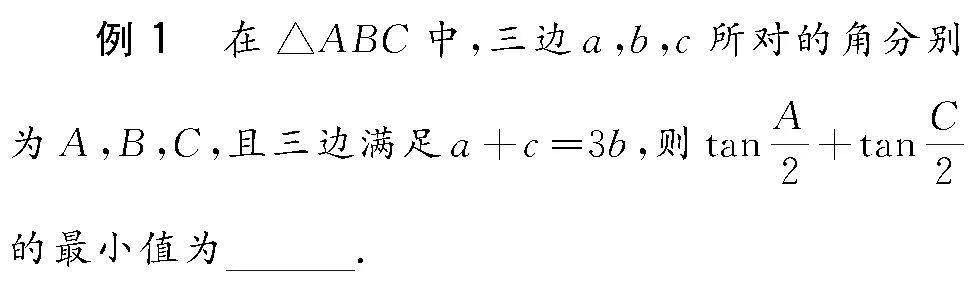
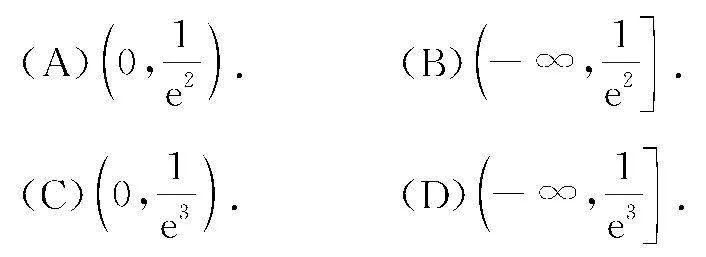
【摘要】齐次化策略是解决数学中一些相关代数关系式的变形与转化时一种特殊的技巧与策略，是解决数学应用问题的基本技巧之一．本文就齐次式的构建处理几类结合三角函数、函数与方程以及圆锥曲线等问题，并对技巧方法进行归纳总结．

【关键词】齐次式；高中数学；解题技巧

解决一些涉及代数关系式的函数与方程、不等式、三角函数、圆锥曲线等相关应用问题，经常根据题设条件或解析过程中代数关系式的结构特征或本质属性，借助自身敏锐的眼光与视角，洞察代数关系式的内涵，合理构建对应的齐次式，结合齐次化策略与应用，是分析与解决相关问题中一种行之有效的技巧方法，倍受大家关注．本文结合实例，就齐次式的构建与应用加以剖析，抛砖引玉．

1 构建齐次式解决三角函数（或解三角形）问题

三角函数（或解三角形）问题中，经常有齐次化策略的影子．在解决一些相关的三角函数（或解三角形）问题时，特别是涉及sinx，cosx等三角关系式的齐次结构，合理利用齐次式的构建与转化，灵活代换，巧妙变形，综合三角函数或解三角形中的相关知识、公式等来巧妙求解与应用．

分析 根据题设条件中三角形的边的关系式，利用解三角形思维化边为角，实现三角形中角的统一性，结合三角形的基本性质以及三角恒等变换公式等加以恒等变形，通过齐次式的构建与变形，得以确定三角函数关系式的定值问题，并结合基本不等式来确定相应的最值即可．

解 由正弦定理，可知a=2RsinA，

b=2RsinB，c=2RsinC，

其中R为△ABC的外接圆半径，

结合a+c=3b，

点评 在解决涉及三角函数（或解三角形）问题中的形如sinx，cosx的齐次结构问题时，经常通过常数代换、公式变形、换元处理、整体思维等方式，综合齐次化策略与三角函数关系式，合理变形，巧妙应用．

2 构建齐次式解决函数与方程（或不等式）问题

抓住函数与方程（或不等式）问题的结构特征，是齐次化策略应用的一个重要场所．在解决一些相关的函数与方程（或不等式）问题时，利用齐次式的构建与转化，实现对应函数中多元问题的递减法处理，减少变量的个数，特别是结合整体思维或换元变换等处理，可以优化解题过程，提升解题效率．

例2 （2022年安徽省安庆市高三模拟考试（二模）数学试题（理））若存在两个正实数x，y使得等式x（2+lnx）=xlny－ay成立，则实数a的取值范围是（ ）

分析 根据题目条件，通过对相应的等式加以恒等变形，巧妙分离参数，有针对性地通过两次换元处理，进行齐次式处理，合理构建对应的函数，利用函数与导数及其应用来确定函数的最值，进而得以求解相关参数的取值范围．

解 依题中等式x（2+lnx）=xlny－ay，

令f′（m）=0，解得m=e，

则当m∈（0，e）时，f′（m）>0，函数f（m）在区间（0，e）上单调递增；

当m∈（e，+∞）时，f′（m）<0，函数f（m）在区间（e，+∞）上单调递减，

故选择答案：（D）．

点评 借助齐次式的构建，有效转化函数与方程问题中的等式，为进一步换元处理与函数构建提供条件．在解决函数与方程（或不等式）问题中，要求具备较强的观察能力与数学运算能力，需要对条件中的关系式进行必要的变形处理，合理构建齐次式，为问题的分析与解决指明方向．

3 结语

抓住相关数学问题的本质，特别是代数关系式的结构特征或特殊形式等，结合代数式的齐次化策略，合理构建齐次式，通过较强的变形能力进行恒等变形与转化，巧妙转化相应各项整式、分式中关系式的次数，或整体处理，或换元变换，为问题的进一步解决与处理提供更加广阔的空间，从而强化逻辑推理，优化数学运算，拓展数学思维，提升数学能力，培养核心素养．