“恒成立问题”与“存在性问题”的基本解题策略

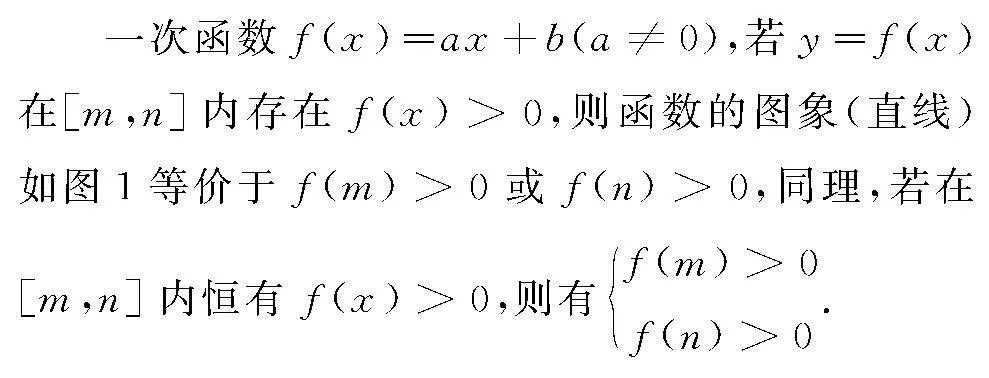
【摘要】在新课标下的高考注重对学生综合能力的考查，而恒成立问题和存在性问题是考查学生综合素质的重要途径.本文将介绍这两类数学问题的基本类型，通过对这两类数学问题的特点和解题方法进行分析，总结了常见的解题策略，并对具体案例进行分析，展示了这些策略在解决实际问题中的应用.

【关键词】恒成立问题;存在性问题;解题策略

恒成立问题与存在性问题是数学中常见的两类问题，解决这两类问题需要我们灵活运用数学知识和技巧，具有一定的逻辑推理能力和创造性思维，总结一些常见的解题方法，具体研究如下：

1 “恒成立问题”与“存在性问题”的基本类型

设函数fx，gx，对任意的x1∈a，b，存在x2∈c，d，使得fx1≥gx2，

则fxmin≥gxmin.

2 基本的解题策略

2.1 一次函数型

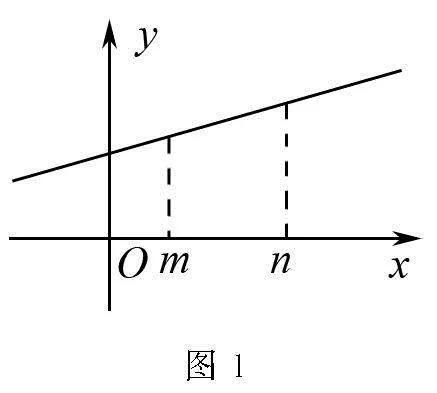
例1 若x∈（－2，2），不等式kx+3k+1>0恒成立，求实数k的取值范围.

解 构建函数f（x）=kx+3k+1，转化为f（x）在x∈（－2，2）内恒大于零.

当k=0时，有f（x）=1>0恒成立；

当k≠0时，f（x）为一次函数，等价于f（－2）>0，f（2）>0

解得k∈（－1，+∞）.

2.2 二次函数型

若二次函数y=ax2+bx+c（a≠0）大于0恒成立，存在有a>0且Δ<0.

类型1 设a>fx在R上恒成立.

f（x）>0在x∈R上恒成立a>fxmax；

（2）f（x）<0在x∈R上恒成立a>fx.

类型2 设在区间［α，β］上恒成立.

（1）当a>fxmin时，

综上所述，f（x）的定义域为R时，a∈［1，9］.

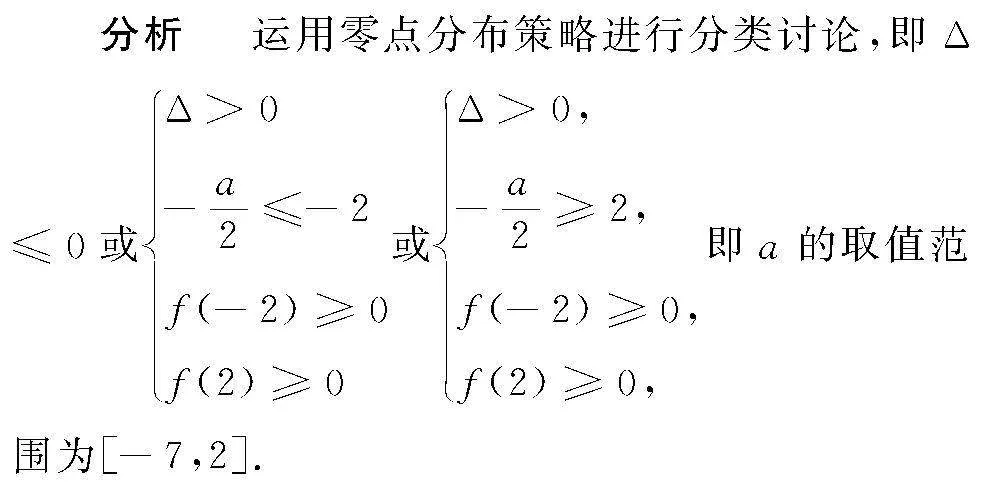
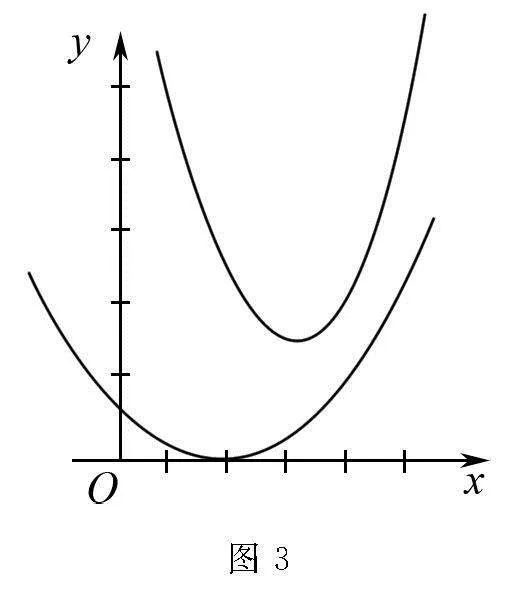
例3 已知函数f（x）=x2+ax+3－a，在R上f（x）≥0恒成立，求a的取值范围.

分析 函数图象都在x轴及其上方，如图3所示.

略解Δ=a2－43－a=a2+4a－12≤0，所以－6≤a≤2.

变式1 若x∈－2，2时，f（x）≥0恒成立，求a的取值范围.

希望通过本文所提供的方法，读者能够更加自信地应对各种“恒成立问题”与“存在性问题”.在解题过程中要灵活运用所学的数学知识，善用各种解题策略，并鼓励培养创造性思维，勇于尝试不同的方法来解决问题.解决数学问题的过程不仅仅是得出答案，更重要的是提高自己的逻辑推理能力和问题解决能力.

参考文献：

[1]张长明.浅谈有关恒成立问题的解题策略与技巧[J].科技信息，2011（07）：211.

[2]武开宏，杨子林.例析与数列有关的不等式恒成立问题的解题策略[J].数学学习与研究，2012（17）：85.

[3]高恬宇.例谈一类不等式恒成立问题的解法[J].语数外学习（高中版上旬），2023（07）：32.