三角函数在解三角形问题中的应用探究

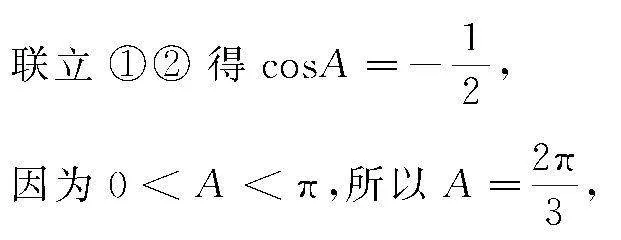
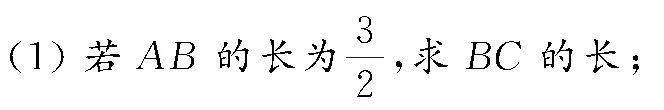
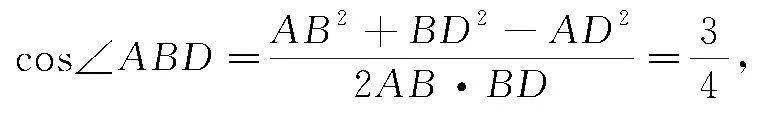
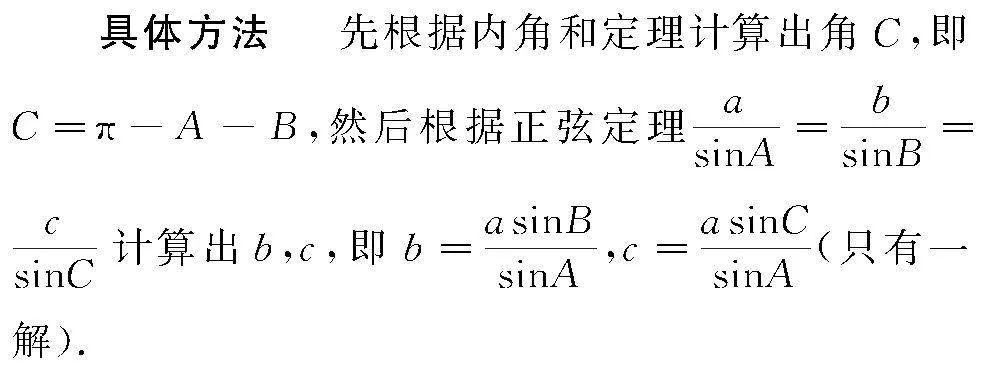
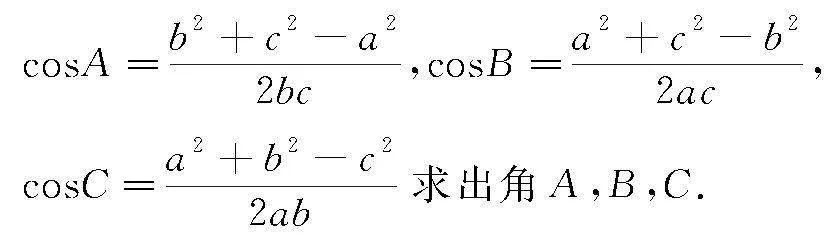
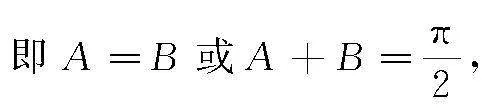
【摘要】在三角函数中，利用正弦定理、余弦定理解三角形或者求解平面几何图形中有关量的问题是高考的热点、重点问题，需要综合应用两个定理及三角形有关知识进行解答，考查学生对条件的转化能力.本文对三角函数在解三角形问题中的应用进行探究，并列举例题进行分析解答，以期帮助学生更加熟练地运用三角函数知识解答解三角形问题.

【关键词】三角函数；解三角形；高中数学

三角形是几何学中重要的图形之一，正弦定理和余弦定理的学习可以帮助我们更好地理解三角形的性质和特点.同时，正弦定理、余弦定理、三角恒等变换也是解决三角形中各种角度和边长关系的重要工具，通过这些定理和工具的运用，一些常见的三角形问题可以得到简单快速的解决.

1 利用正弦定理解三角形

（1）已知△ABC的两角A，B及一边a，求角C和边b，c.

（2）已知△ABC的两边a，b及一边的对角A，求边c和角B，C.

为2，角B为120°，求BC的长.

点评 利用正弦定理可以对三角形的边角进行转化，一般是都转化为边或都转化为角，边角一致有利于解题.

2 利用余弦定理解三角形

（1）已知两边a，b及夹角C，求第三边c和其他两角A，B.

（2）已知三边a，b，c（或三边的关系），求角A，B，C.

具体方法 直接根据余弦定理的变形式

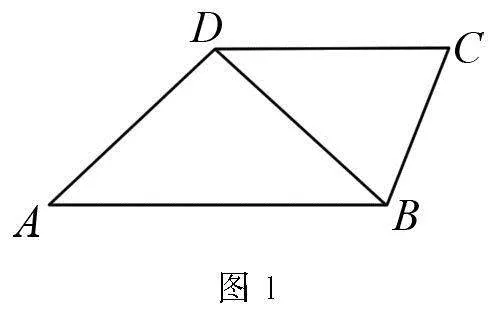
例2 如图1所示，在四边形ABCD中，已知AD，CD，BD的长均为1，且AB∥CD.

（2）若AB的长为BC的2倍，求cos∠BDC.

解 （1）在△ABD中，由余弦定理可得

因为AB∥CD，

所以∠BDC=∠ABD，

在△BCD中，由余弦定理可得

（2）设BC=x，则AB=2x，

在△ABD中，由余弦定理可得

由（1）知∠BDC=∠ABD，

所以cos∠ABD=cos∠BDC，

点评 涉及角的范围，遇到a2，b2，c2等，一般可以利用余弦定理进行求解.

3 利用正、余弦定理判定三角形形状

利用正、余弦定理判定三角形形状有两种解题思路，一种是先通过正弦定理和余弦定理，将边与边之间的关系化为角与角之间的关系，再利用三角变换，求出三角形三个内角之间的关系，然后判断三角形形状；另一种是通过正弦定理和余弦定理，将角与角之间的关系化为边与边之间的关系，再通过代数恒等变换，得到三条边之间的关系，然后判断三角形形状.

例3 在△ABC中，三个内角A，B，C的对边分别用a，b，c表示，如果（a2+b2）sin（A－B）=（a2－b2）sin（A+B），请判断△ABC的形状.

解 已知等式可化为

a2sin（A－B）－sin（A+B）

=b2－sin（A-B）－sin（A+B），

所以2a2cosAsinB=2b2cosBsinA，

由正弦定理，上式可化为

sin2AcosAsinB=sin2BcosBsinA，

因为sinA≠0，sinB≠0，

所以sinAcosA=sinBcosB，

即sin2A=sin2B，

由A，B∈0，π，

得0<2A<2π，0<2B<2π，得2A=2B或2A+2B=π，

所以△ABC为直角三角形或等腰三角形

点评 解答三角形形状判断类题型时，要注意是否有多个解，注重挖掘题目隐含的条件，不可推算错漏.

4 三角恒等变换与解三角形

三角恒等变换与解三角形的综合题一般有两种类型：一是先利用三角函数的平方关系、和角公式等，求出符合正弦定理、余弦定理中的边与角，再利用正弦定理、余弦定理求值；二是先利用正弦定理、余弦定理确定三角形的边与角，再代入到三角恒等变换中化简求值.而对于三角函数性质、三角变换及图象变换、解三角形等相结合类型的综合问题，求解时要理清思路，先把异名、异次、异角化异为同，最终化为一个函数一个变角的三角函数式，再根据相应知识逐一解决.

例4 在△ABC中，已知BC的长为3，且sin2A－sin2B－sin2C=sinBsinC，

（1）求A；

（2）求△ABC周长的最大值.

解 （1）由正弦定理和已知条件得

BC2－AC2－AB2=AC·AB①=1，

由余弦定理得

BC2=AC2+AB2－2AC·AB·cosA②=2，

（2）由正弦定理及（1）得

点评 与三角形有关的问题主要有两种：一是解三角形求出有关量，利用公式求面积或周长；二是将面积或周长作为已知条件之一，利用正弦定理和余弦定理求解三角形中的其他量.

5 解三角形的综合应用

解三角形的综合应用类问题，要充分利用正、余弦定理实现边角互化，然后利用三角函数的和差、倍半公式进行三角恒等变换，进而求出结果，得出结论.

（1）求角B的大小；

（2）求cosA+cosB+cosC的取值范围.

点评 解与三角形中边角有关的量的取值范围时，主要是利用已知条件和有关定理，将所求的量用三角形的某个内角或某条边表示出来，结合三角形边角的取值范围、函数值域的求法求解范围即可.

6 结语

总的来说，正弦定理和余弦定理是解决三角形中角和边关系的重要工具，利用正弦定理和余弦定理，可以把题干给的已知条件转化为三个内角与三边之间的三角函数关系，然后通过三角函数恒等变形，找到三角形内角以及三边之间的关系，不论是在数学学习，还是在实际问题中都有着重要的应用价值.

参考文献：

[1]周丽娇.开放探究，创新应用——三角函数及解三角形问题[J].中学生数理化（高考数学），2023（01）：17-19.

[2]陆萍，王剑.重视逻辑推理关注全局变化——2022年高考“三角函数与解三角形”专题解题分析[J].中国数学教育，2022（Z4）：41-47+57.

[3]杨永健，夏林林，张晓斌.探根源凸本质重思想育素养——2023年高考“三角函数与解三角形”专题解题分析[J].中国数学教育，2023（Z4）：39-46.

[4]林运来.“三角函数与解三角形”专题解题分析[J].数学通讯，2023（13）：54-57.