高中数学解题中化归思想的应用

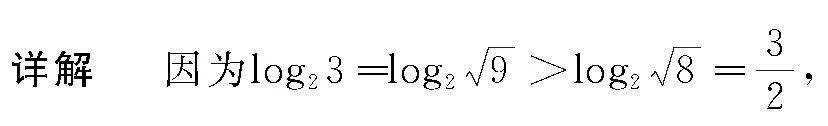
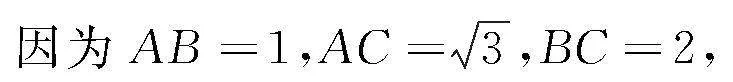
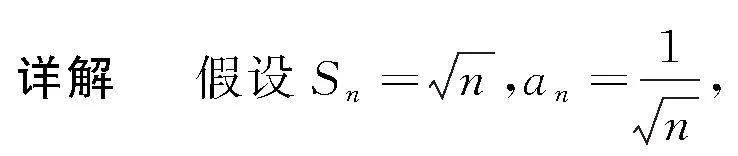
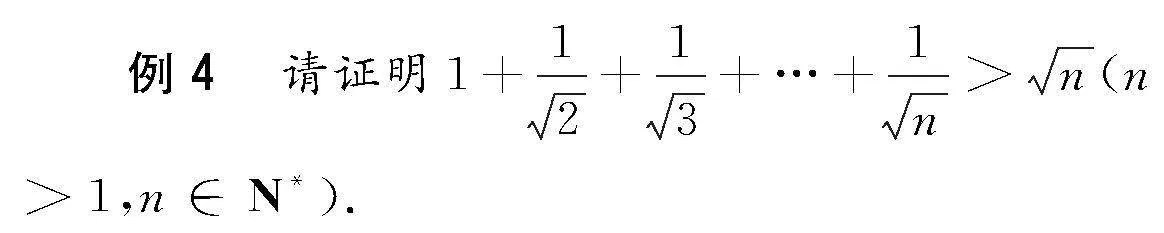
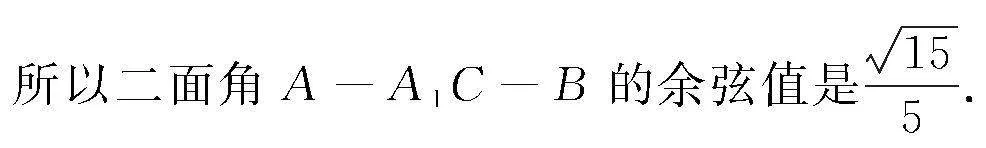
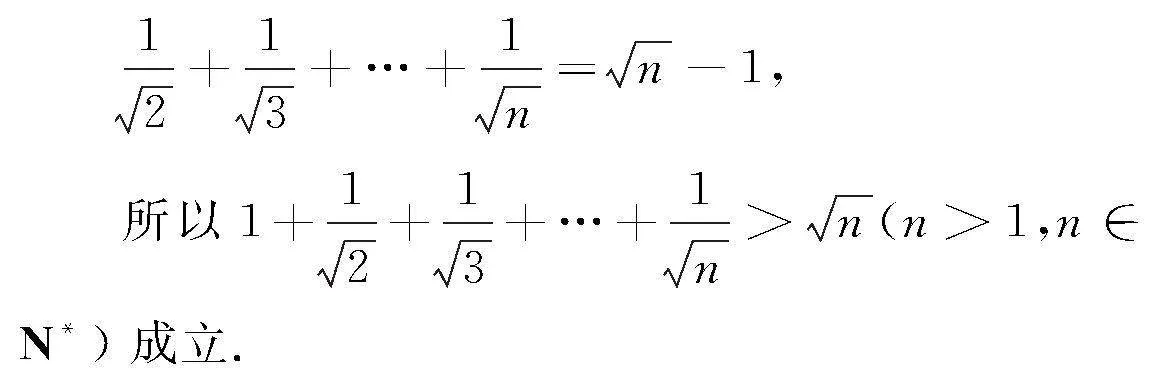
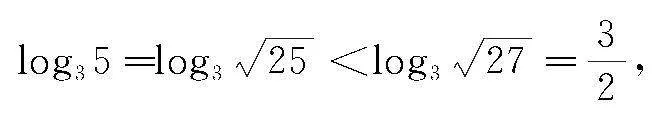
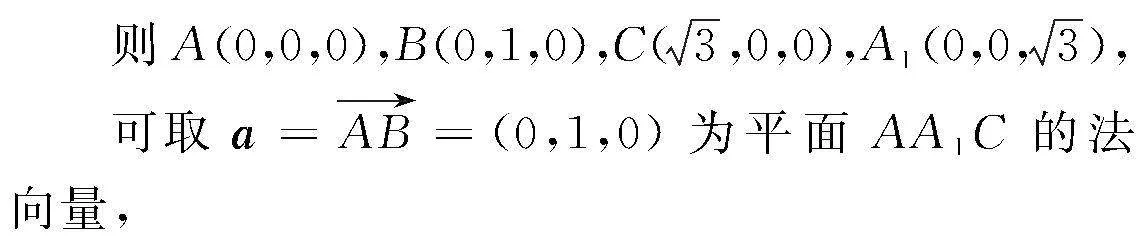
【摘要】解题教学属于高中数学教学中的一个常规环节，主要训练学生运用所学理论知识进行解题的能力，使学生通过实践做题掌握一些常用的解题技巧，为高考做准备.化归思想作为一个比较常见的数学思想，既能够用来学习理论知识，还广泛适用于解题，高中数学教师需帮助学生学会应用化归思想来解题，逐步提高他们的数学解题水平.本文主要对高中数学解题中如何应用化归思想进行分析和探讨，并分享一些解题实例以供参考.

【关键词】高中数学；解题技巧；化归思想

1 引言

化归思想就是把一个问题由繁化简、由复杂化简单、由难化易的过程，属于转化与归结的统称.化归思想不仅是一种比较常用的解题思想，还是基本解题思维策略的一种.在高中数学解题训练中，会涉及各种类型、形式各异的题目，当使用常规方法解题难度较大或者比较复杂时，教师就可以指导学生尝试应用化归思想，使其通过题目中某些条件的转化或者归结，精准地把握解答这一试题的关键点，使其解题速度与准确度均有所提升[1].

2 应用动静化归，解答数学试题

例1 请比较对数值log23与log35的大小.

分析 处理这一题目时可直接采用化归思想，利用函数的动态和静态之间的化归处理问题，先认真观察这两个对数式子，明确这两个函数式子均属于静止数值，再应用化归思想，借助静态和动态的转换，建立相应的对数函数f（x）=log2x与f（x）=log3x，然后把这两个函数式子看成函数自变量对应的函数值，由此实现数值静态化向动态化的转换，结合换底公式对这两个对数式子的大小进行比较[2].

所以log23>log35.

3 应用数形化归，解答数学试题

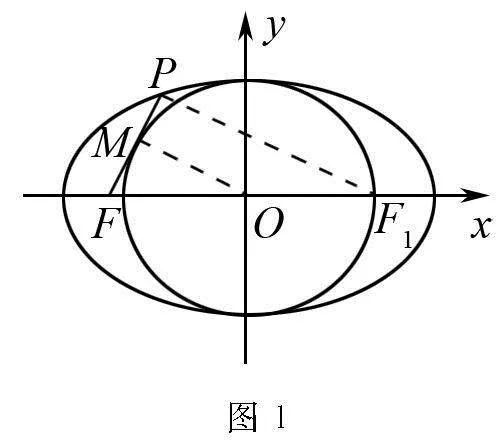
分析 处理这道题目时可借助数形结合的化归思想，根据题意画出相应的图形，实现“数”向“形”的化归，如图1所示，设右焦点为F1，把PF1，OM分别连接起来，随后结合三角形的中位线定理、圆的切线性质、椭圆的定义等知识完成解题.

详解 根据题意画出图1，当切点为M时，连接PF1，OM.

因为M，O分别是PF，FF1的中点，

所以PF1∥MO，且|PF1|=2|MO|，

又因为线段PF和圆O相切于点M，

所以OM⊥PF，PF⊥PF1，

4 应用等价化归，解答数学试题

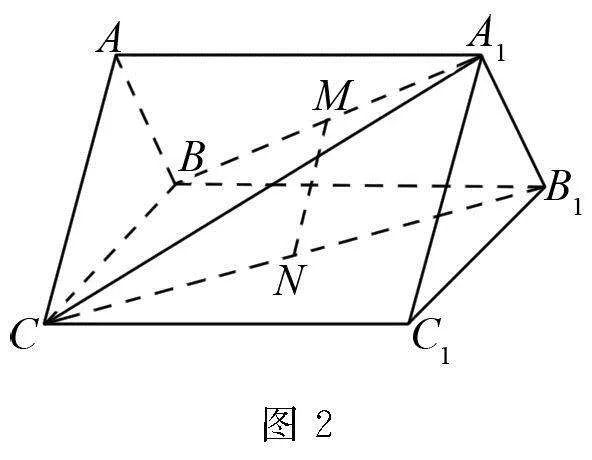
分析 解答这一题目时通过对已知条件的分析需采用化归思想，以原图为基础建立一个空间直角坐标系进行等价化归，得到关键点的坐标，不过需保证条件、数据的等价性，不能同原题相悖，然后利用向量知识求解异面直线的夹角，从而求出这个二面角的余弦值大小.

详解 因为三棱柱ABC－A1B1C1是一个直三棱柱，

所以AB⊥AA1，AC⊥AA1，

所以AB2+AC2=BC2，

故AB⊥AC，

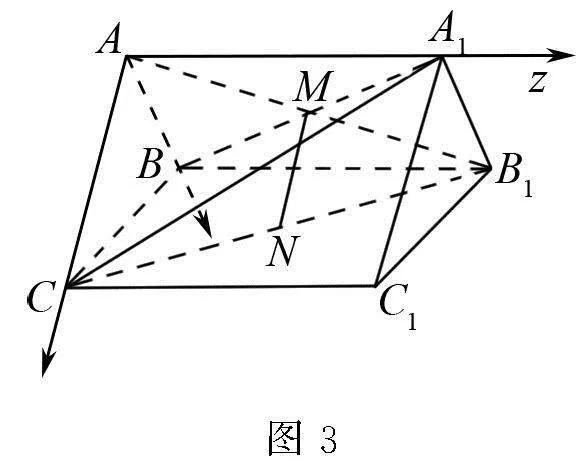
如图3所示，构建一个空间直角坐标系，

设平面A1BC的法向量是b=（m，l，n），

5 应用等式化归，解答数学试题

分析 处理这样一道复杂的不等式题目时，将题目中的不等号“>”当作是“=”展开思考，实现不等式向等式的转换，即为对化归思想的应用，采用证明等式的数学思想方法证明不等式相关问题[3].

则原问题化归成an=Sn－Sn－1（n>1，n∈N*）能够成立，

结合等式与不等式之间的关系可把原题转换成证明an>Sn－Sn－1成立，

将两边相加以后能够得到等式

6 结语

总的来说，在高中数学解题教学实践中，教师应充分意识到化归思想在解题中的作用和功能，在平常讲授理论知识的过程中注重化归思想的渗透，帮助学生打牢理论基础，从而在解题中能够尽可能发挥出化归思想的价值，使其学会应用化归思想优化解题流程和思路，进而找准解题的突破口，最终让他们在化归思想的辅助下摆脱难题障碍，增强解题的自信心.

参考文献：

[1]郭琼梅.化归思想在高中数学解题中的应用研究[J].数理化解题研究，2023（24）：8-10.

[2]胡长才.浅谈高中数学解题训练中化归思想的巧妙运用[J].数理天地（高中版），2023（15）：29-30.

[3]杨军文.转化与化归思想在高中数学解题中的应用[J].数理化解题研究，2023（21）：50-52.